井下防喷器坐封后多相流瞬态流动规律研究

2022-03-07胡艺凡马兰荣尹慧博

西南石油大学学报(自然科学版) 2022年1期

谷磊，胡艺凡，马兰荣，尹慧博，李皋

1.中国石化石油工程技术研究院，北京朝阳 100101

2.油气藏地质及开发工程国家重点实验室·西南石油大学，四川成都 610500

引言

随着油气开发的不断深入开展，勘探目标逐渐转向深部地层，在钻井过程中，井漏、气侵、溢流等复杂情况多发，井控风险极大。常规钻井过程在发生溢流、井涌后通过井口防喷器防止井喷的发生，井口防喷器坐封后井筒侵入大量高压气体使套压升高，压井难度大、周期长、成本高。若能充分利用井下防喷器，将井下防喷器与钻柱连接，在钻进、起下钻过程发生溢流、井涌时，井下防喷器坐封实现危险层环空封隔，并建立循环通道、提供压井条件，相当于将井口防喷器移至井下，能够将高压气体控制在源头、减小井口压力，有效降低井控风险[1-2]。因此，井下防喷器有较大的应用前景。

虽然井下防喷器在高压、超深、高温区块具有显著的优点，但目前在现场应用时仍存在一些问题，主要表现在两个方面：（1）当井下防喷器坐封后，下部井筒仍受气侵的影响，井筒压力持续增高，对井下防喷器的密封性能造成考验，甚至还有压漏地层的风险；（2）井下防喷器坐封后地面的立压、套压等录井数据不能够真实反映防喷器下部井筒的真实流动情况，常规的压井理论难以适应。

针对井下防喷器的研究工作主要涉及井下防喷器的设计与坐封功能实现[3-5]，密封性能与稳定运行分析[6-9]，应力分析[10]，室内实验与仿真研究[11-12]等。井下防喷器的流动实质上是密闭空间内的多相流流动，涉及井筒-储层内的物质交换，对于井筒地层多相流的研究，已经深入到较为复杂的研究阶段[13-16]。同时，井下防喷器的流动过程与关井过程中的井筒内流动也很类似，在这方面也有许多研究[17-19]。但对于其坐封后井筒多相流瞬态流动规律的研究较少，尚未见有价值的研究成果。正因如此，井下防喷器的概念提出已约40 年，仍处于地面试验或样机试制阶段，还未大规模工业化应用。

目前，针对井下防喷器井筒压力控制理论的研究近乎空白，常规钻井井筒多相流及井筒压力控制理论研究成果虽然能够提供必要的理论参考，但由于井下防喷器坐封后上部井筒重新建立循环，井筒被分割为上部井筒和下部井筒，井筒多相流流动边界发生变化，常规钻井井筒多相流理论无法适应下部井筒的真实情况，常规井控理论无法适用。为此，针对井下防喷器坐封后下部井筒复杂流动特性，建立一套防喷器坐封后下部井筒地层-井筒耦合瞬态流动数学模型并进行数值求解，得出全井筒的压力演变规律，为井下防喷器结构设计、安全作业时间及井下防喷器井筒压力控制工艺提供必要的理论依据。

1 井下防喷器坐封后流体动力学分析

1.1 井下防喷器工作过程

井下防喷器最早的提出源于海洋钻井。海洋钻井过程中由于地层结构脆弱，采用重浆压井可能会破坏储层，导致事故频发，为此，开始研制井下防喷器。井下防喷器是一种井下的井控工具，主要功能是在溢流或者井喷的时候能够坐封切断环空体积内的物质运移，同时，在解封之后能够继续保持物质运移。常用的井下防喷器包括旋塞阀式防喷器、插板阀式防喷器以及提升阀式防喷器。

本文所述的井下防喷器与钻柱连接，当钻进、起下钻过程中溢流、井涌出现时，井下防喷器坐封实现危险层环空封隔。封隔后下部井筒存在一定的体积，会持续受到气侵的影响，地层中的流体会继续进入到井筒内直到地层与井底的压力平衡。井筒压力升高时，在防喷器下气柱压力不高于胶筒最大承压能力的时间区间内都可进行压井作业循环。在此时间内，循环压井使井下压力平衡，井下防喷器解封继续正常钻进，其工作过程如图1 所示。

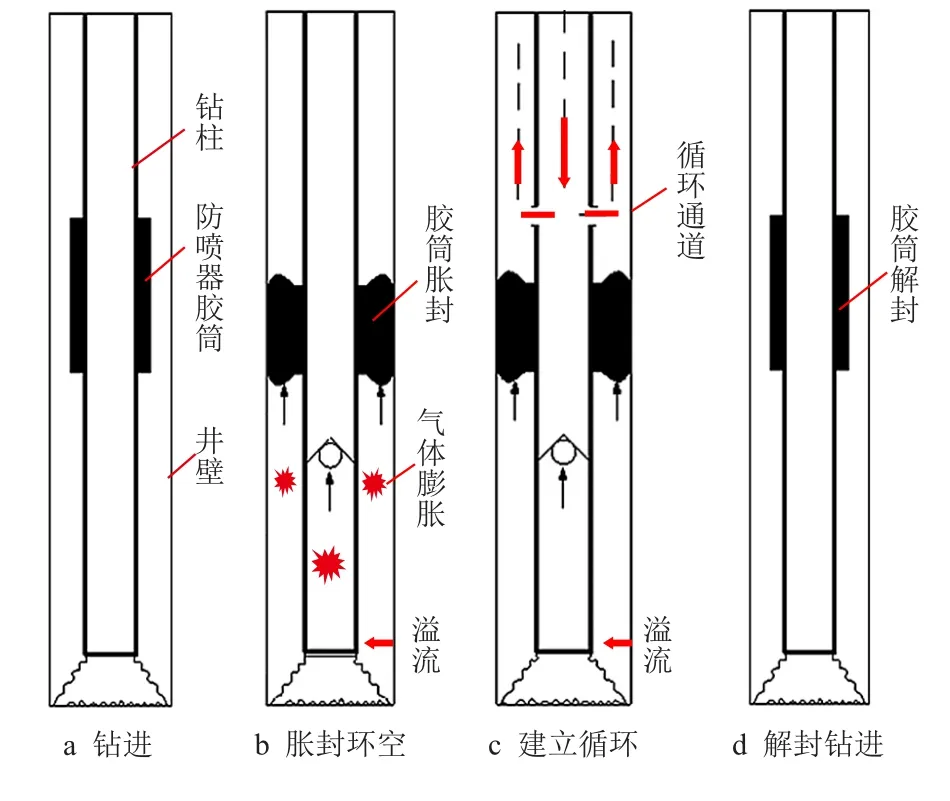
图1 井下防喷器示意图Fig.1 Schematic diagram of down-hole BOP

1.2 防喷器坐封后多相流瞬态流动模型

1.2.1 井筒多相流流动基本模型

当井底发生气侵或者溢漏同存时，井下防喷器进行坐封。此时防喷器下部流动空间包含气液两相，采用气液两相漂移流模型，控制方程组包含两个连续方程和一个混合动量方程

为了进一步使方程组封闭，需要引入相关的辅助方程，主要包括以下方程。

体积分数归一化方程

重力源项方程

摩擦阻力源项方程

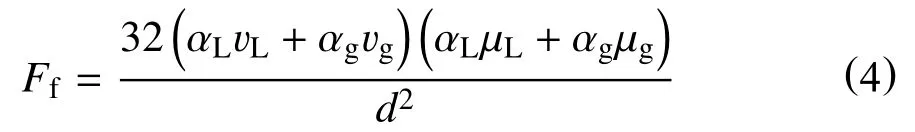
液体状态方程

气体状态方程

滑脱关系采用Zuber 漂移关系式

1.2.2 井筒流动阶段模型

（1）井筒续流效应阶段

在井下防喷器关闭后，由于防喷器下部到井底的管柱存在体积空间，而气体和液体都具有可压缩性，所以地层中的气体还会持续进入到井筒改变流动动态。结合质量守恒定律与空间体积关系，井筒内体积流入之差等于气体膨胀、液体压缩与井筒膨胀3 部分体积改变之和[20]

如果为单纯气侵，防喷器坐封初期的井底压力小于地层压力，井筒内流体不会渗透到地层中，Qgout=0。如果为漏喷同存，Qgout则为漏失流量。由于井筒的弹性相比钻井液和气体压缩性小，可忽略。

（2）气体滑脱上升效应阶段

在重力差异的作用下，气液两相发生分离，气体滑脱上升。气体在上部受到的压力较小，发生膨胀，防喷器下部压力会增加。当气体滑脱上升时，气体因膨胀增大的体积等于钻井液因受压减少与钻井液滤失减少的体积之和，则有

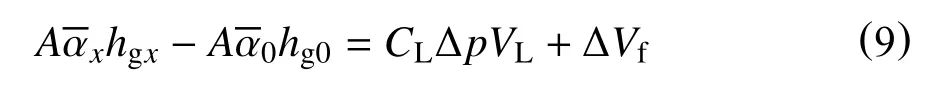
1.2.3 模型求解

应用上述模型可以计算出井下防喷器坐封后井筒复杂多相流瞬态流动规律，其计算流程如图2所示。

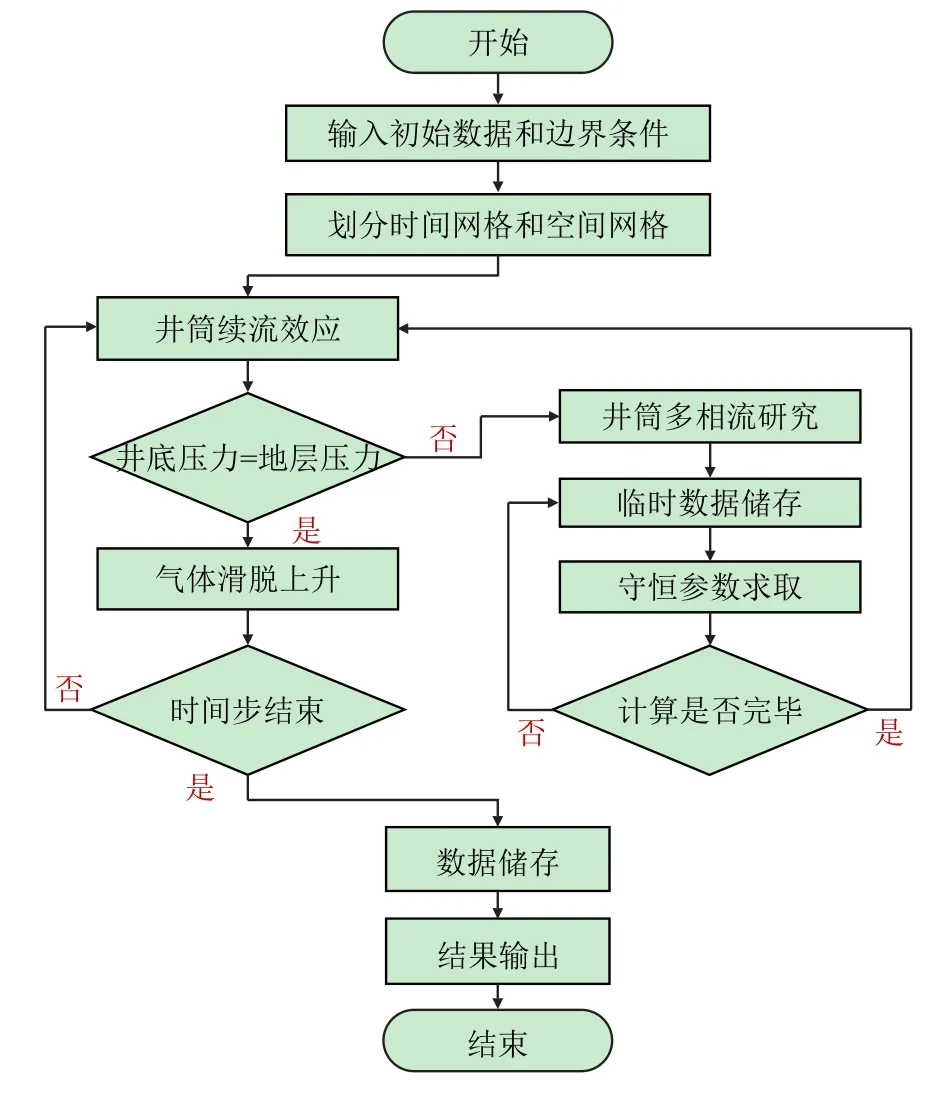
图2 计算流程图Fig.2 Calculation flow chart

通过计算，可以得到井下防喷器作业后不同管段的压力动态分布以及瞬态演变规律，从而获得井口压井循环的安全作业时间。

2 防喷器坐封井下瞬态流动数值模拟

通过计算不同参数下井下防喷器坐封后压力演变情况从而得出压力分布规律性的认识，可为井下防喷器结构设计、安全作业时间及井下防喷器井筒压力控制工艺提供必要的理论依据，数值计算结果与分析如下。

2.1 防喷器坐封期间井筒多相流变化特征

在实际钻进过程中，当钻遇储层时，地层流体在压差的作用下进入到井筒，井筒内的流动状态发生改变，井底的压力也发生改变。在地面决定井下防喷器坐封时，井筒内实际上已经侵入了流体，为此需要结合其他辅助手段判断气体流入的情况，然后分析防喷器坐封的时刻和坐封后的受力状态。在模拟过程中，可设定气体侵入的时间节点，改变时间节点，瞬态的流动过程会相应改变。

2.1.1 基本参数

井深：7 000 m；裸眼直径：114.3 mm；技术套管直径：168.28 mm；钻杆直径：139.7 mm；技术套管下深：2 900 m；钻井液密度：1 210 kg/m3；钻井液排量：12 L/s；井口回压：0.1 MPa。钻遇92.4 MPa 高压地层、防喷器坐封，防喷器分别下深6 000，5 000 和4 000 m。

模拟工况条件：在50 s 内，液体不循环，50～150 s 内，液体开始循环，150 s 时，气体开始侵入，在500 s 时，防喷器坐封。

地层性质：孔隙度为13%；渗透率为0.5 mD。

2.1.2 压力分布分析

图3、图4 和图5 分别为防喷器下深6 000，5 000和4 000 m 时的压力分布图。

图3 防喷器下深6 000 m 时压力分布图Fig.3 Pressure distribution of down-hole at depth of 6 000 m

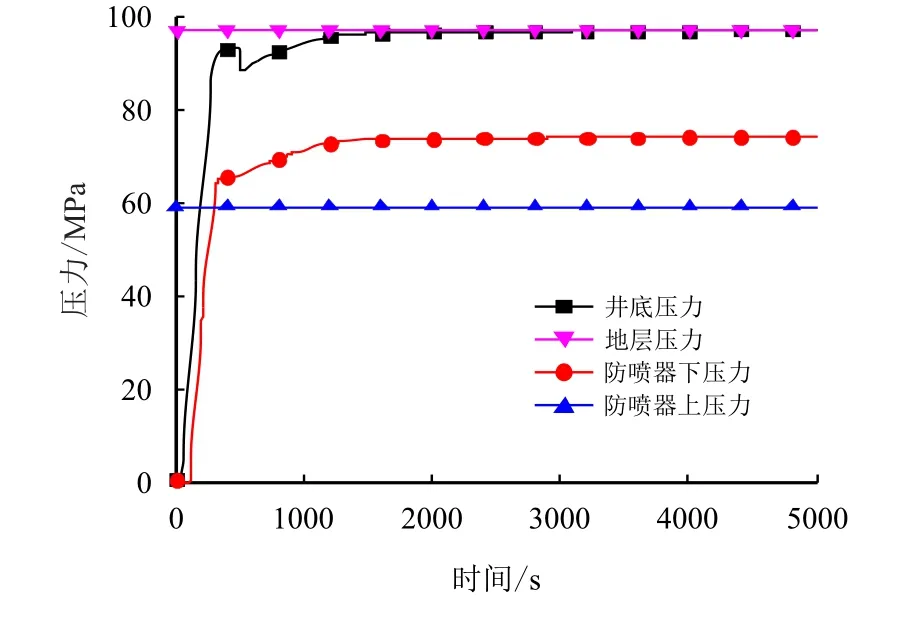
图4 防喷器下深5 000 m 时压力分布图Fig.4 Pressure distribution of down-hole at depth of 5 000 m

从图3～图5 可以看出，防喷器不同下深情况井筒压力演变规律基本相同：随着气侵量的增加，井底压力急剧增加后逐渐趋于稳定，最终井底压力与地层压力基本平衡；防喷器下部压力先上升后逐渐平稳。防喷器下深6 000，5 000 及4 000 m 时，压力稳定时间分别为坐封后626，735 和851 s，防喷器下的压力分别稳定在85.2，75.3 和64.4 MPa。

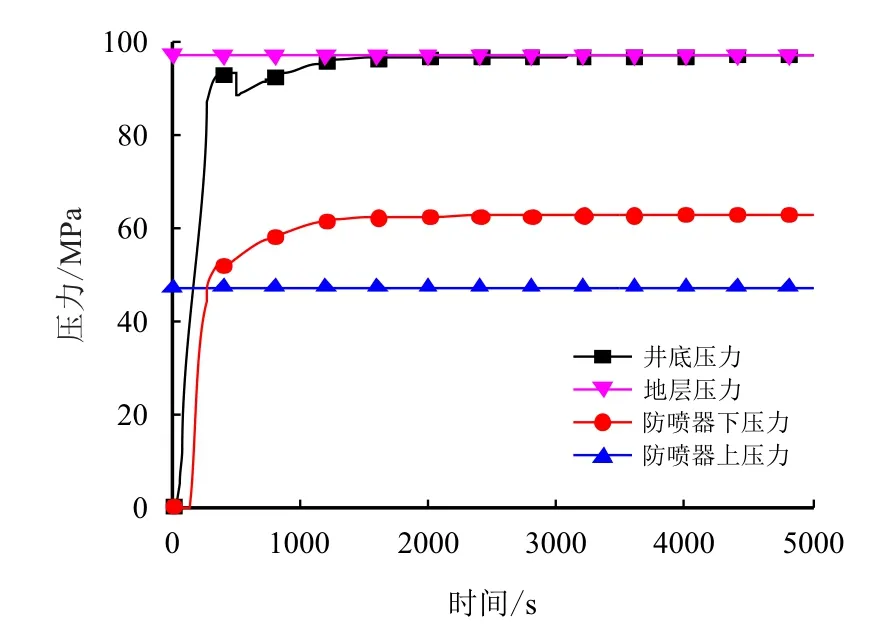
图5 防喷器下深4 000 m 时压力分布图Fig.5 Pressure distribution of down-hole at depth of 4 000 m

2.2 井底压力影响因素分析

计算不同影响因素下井下防喷器坐封后井底压力，得到其演变情况，进而分析井下防喷器坐封后井底压力的影响因素。

2.2.1 基本参数

为分析防喷器坐封期间井筒压力变化特征，采用基本参数：井深3 000 m；地层压力50 MPa；渗透率10 mD；钻井液密度1 200 kg/m3；钻井液排量20 L/s；钻井液黏度20 mPa·s。

2.2.2 初始井底压力

为了分析相同地层压力条件下不同初始井底压力的压力动态变化，分别设置井底压力为42，45 和48 MPa，计算结果如图6 所示。

从图6 中可以看出，随着时间的增加，井底压力都呈指数增加，并最终接近地层压力。初始井底压力越小，则进入到井筒的流量越大，井筒内的气液和液体都会受到明显压缩，压力传递更为迅速，所以压力梯度更大。

图6 不同初始井底压力下的井底压力演变规律Fig.6 Variation of bottom-hole pressure at different initial bottom hole pressures

2.2.3 地层渗透率

为了分析渗透率对井底压力的影响，分别设置地层渗透率为0.01，0.03 和0.05 D，井底压力随着时间的变化曲线如图7 所示。可以看出，地层渗透率越大，井底压力变化的速度也就越快，到达地层压力的时间也就越短。根据前面建立的模型可以看出，随着地层渗透率的增加，地层流体进入到井筒的通道也就越大，单位时间流入到井筒的流量也就越大，更大的侵入气体体积使得气液两相的压缩体积也就越大，压力也会迅速增加。

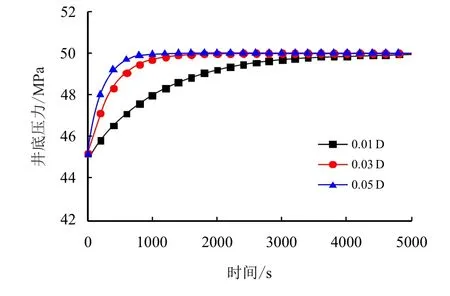
图7 不同地层渗透率下的井底压力演变规律Fig.7 Variation of bottom-hole pressure at different formation permeability

2.2.4 防喷器下深

为了分析防喷器下深对井底压力的影响，分别设置防喷器距井底2 000，2 500 与3 000 m，井底压力的影响如图8 所示。可以看出，防喷器坐封期间，对于不同的防喷器下深位置，到达稳定的时间不一样。对于不同的防喷器下深，储存气液两相的空间不同，防喷器下深越深，则储存空间越小，续流效应和滑脱效应带来的压缩效应越明显，从而导致压力变化更为迅速。防喷器下深位置越深，压力稳定越迅速，其下部承受的压力迅速增大，需要考虑防喷器本身的抗压能力，避免其在井口采取相应措施之前被刺穿，导致坐封失效。