改进遗传算法求解带时间窗的外卖配送车辆路径规划
2022-03-07赵家儒谭代伦
赵家儒,谭代伦
(1.西华师范大学数学与信息学院,四川南充 637009;2.西华师范大学计算方法及应用软件研究所,四川南充 637009)
0 引言
随着现代制造业和物流业的快速发展,车辆路径规划问题(Vehicle Routing Problem,VRP)[1]得到重视和研究,Dantzig等在1954年研究汽油运输卡车的最优路径时首次提出该类问题[2],并将其描述为:对给定的一组客户,为从某个特定配送中心出发的运输车辆规划出最优行驶路线,使得在满足一定约束条件下行驶成本(如里程数、耗费时间等)尽量少.
针对VRP问题的约束条件,国内外学者提出了车辆容量约束、满足客户时间需求的时间窗约束等典型情形.尤其是后者,在现代社会的快节奏生活中,越来越被社会大众所重视,因此带时间窗的车辆路径规划问题(Vehicle Routing Problem with Time Window,VRPTW)成为VRP问题的一种典型扩展情形.对此类问题,Larsen首次将时间窗和车辆路径问题相联系,并进行了分析和研究[3].
随着现代餐饮企业开启O2O服务新模式,餐饮外卖的最优配送引起了研究者的浓厚兴趣,部分研究者将VRPTW问题迁移到这类问题中,形成了带时间窗的外卖配送车辆路径规划问题(Delivery Vehicle Routing Problem with Time Window,DVRPTW).目前对该类问题的研究取得了一些成果,余建军等针对生鲜外卖配送,设计了模糊时间窗,用遗传算法对配送路径进行规划[4];吴球军在硬时间窗的约束下设计了路径规划滞后法和路径规划优先法两种不同思路来进行路径规划[5];刘晓扣等运用遗传算法求解了在外卖员人数和外卖提供能力均无限制的前提下满足时间窗约束的配送路径规划[6];李雪妍为了减少配送平台的人工成本和超时时间,提高配送效率,探究了在派单模式下的配送路径规划[7];黄心等通过蚁群算法对不同地址的收货点进行路径规划,为送货人员规划了最短时间的路径[8];陈火根等针对带时间窗的路径规划问题,提出了遗传算法与启发式算法相结合的求解方法[9];Sophie对一般配送货物类问题进行了综述,归纳和总结了不同的取送货路径问题的特点[10];李卓等提出萤火虫算法与蚁群算法相结合来求解路径规划问题,提高了这类问题的求解效率[11];韩亚娟等以遗传算法作为上层搜索算法,以3种启发式算法—CW节约法、MJ插入法和Kilby插入法作为底层搜索规则,并通过预排序、局部搜索和全局优化来优化算法[13].从现有文献可以看到,DVRPTW问题在求解算法上研究成果还比较少,为此本文提出一种改进遗传算法对该类问题进行求解.
1 问题描述与数学模型
1.1 问题描述
某企业负责城市内餐饮外卖配送业务,企业将一定时间内产生的一组外卖订单分配给某一个配送人员去完成,现考虑为其规划一条最佳路径.在一组外卖订单中,餐饮商家和客户具有一一对应的关系,他们的地图位置也是已知的.配送人员需要从企业特定的配送中心出发,配送的基本规则是同一订单必须先取餐再送餐,即先到指定商家处取得某客户的餐饮外卖食品,再送到该客户处,期间不考虑取餐和送餐时的交接时间.由于外卖餐饮的时效性,取餐和送餐均有时间范围要求,称为时间窗限制,即从订单成立开始计时要尽量在给定的时间范围内取到外卖餐饮或送到客户处,否则配送人员和企业将遭受信用或经济损失.配送过程中不考虑车辆的载重限制,配送人员可以先到多个商家取得多份外卖餐饮,再陆续配送到多个客户手中.配送期间不再接受新的订单,完成全部订单后,配送人员需要回到企业的配送中心,以接受下一批订单.
1.2 数学模型
上述外卖配送车辆路径规划问题,从配送人员行走路径来看,具有旅行商问题(Travelling Salesman Problem,TSP)的基本特征,即从某一个节点出发,经历所有的节点一次且只经过一次,最终回到出发点,因此可借鉴TSP问题来建立本类问题的数学模型.
设在配送人员所承接的一组外卖订单中餐饮商家有n1个、客户有n2个,则配送人员从配送中心0出发,取餐和送餐需要经过的节点总数为n=n1+n2.按一定顺序对所有节点统一编号,记第i个路径节点及其平面坐标为pi(xi,yi),相应的时间窗上限为bi.又有配送人员在配送过程中的行驶速度记为v,且始终是匀速行驶的,任意两个节点pi,pj之间的距离记为dij,所耗费的行驶时间记为tij,取欧式距离公式进行计算,则有
(1)
对由所有路径节点按一定顺序构成的一条回路P={p0→p1→p2→...→pn→p0},就是配送人员的一条配送路径.当配送人员始终以匀速行驶时,配送路径总长度最短与配送行驶时间最短是等价的,并且配送总是要受时间窗限制的约束,于是可建立如下数学模型:
(2)
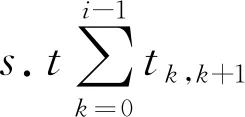
(3)
上述模型的约束条件表示配送人员沿某个回路行驶时,每到达一个路径节点所花费的时间之和应不超过该节点的时间窗上限.
2 改进遗传算法设计
外卖配送车辆路径规划是一类组合优化问题,也是NP-hard问题,求解这类问题的主要方法是现代智能算法.其中遗传算法通过模仿自然界生物的选择与遗传机理来寻求最优解,遗传算法相比于其他算法具有优异的自适应性、并行性和全局寻优能力.已经被广泛应用于求解组合优化问题和NP-hard问题.为此,本文也选择遗传算法进行求解,通过种群修复、自适应交叉与变异等改进策略,进一步提高算法的求解性能.
2.1 编码方案
将上述外卖配送车辆路径规划问题转化为旅行商问题(TSP)后,配送人员取餐和送餐所要经过的商家或客户,就是TSP问题的每一个路径顶点,所有顶点按一定顺序的不重复排列{p1,p2,...,pn}就是配送人员完成全部订单的一条行走路径.为此,本文采用由{1,2,...,n}构成的不重复自然数编码方案,每一个数字对应于一个路径顶点的编号,不同的排列对应于不同的行走路径.由于配送人员总是要从配送中心出发,完成全部订单后要回到配送中心,因此将配送中心也看作是一个路径顶点,编号为0,它始终位于编码序列的起始位置,于是本文算法所采用的最终编码方案形如{0,1,2,...,n},其中经过最后一个顶点后还需要返回到起始顶点处.
2.2 基于修复算子的种群初始化
根据上述编码方案,第一个自然数固定为0,种群初始化时只需生成{1,2,...,n}的任意随机序列即可.由于外卖配送需要满足先到商家取货再到对应客户送货的顺序限制,而在随机初始种群可能会产生不满足顺序限制的个体,因此需要对这部分不满足要求的个体进行修复,其修复步骤如下
(1)种群个体的第一个基因均设置为0,其余基因按均匀分布随机产生[1,n]区间内的不重复自然数;
(2)对每个个体,按订单依次查找商家编号以及与之对应的顾客编号;
(3)判断两者基因位置的先后关系,若商家基因位置处于顾客基因位置之后,则将这两个基因位置交换;
(4)重复(2)与(3),直到所有个体和所有订单全部修复完.
2.3 基于超时惩罚的适应度函数
遗传算法的适应度函数用于评估和区分种群个体的优劣,适应度值是进行遗传选择的依据.由于上述问题是有约束优化问题,因此构造适应度函数时,将原目标函数作为适应度函数的一个分量,如下:
(4)
对约束条件,采用惩罚函数的方法将其变换为适应度函数的另一个分量.在实际生活中,客户的耐心会随着配送人员所超过的时间呈非线性增长,由此选取以2为底的指数函数对超时情形进行惩罚,对应的适应度函数分量如下:
(5)
(6)
其中,T0i表示配送人员沿某个行驶路径到达第i个配送点时所花费的时间总和,可用式(6)予以计算.
综合式(4)(5)(6),本文遗传算法所构造的适应度函数为:
(7)
其中p为所有路径节点构成的任意一个合法的顶点序列,即配送人员的任意一条可行路径.
2.4 选择策略
选择操作是模拟生物种群的“适者生存、优胜劣汰”的自然生存法则,在算法中其目的是选出较优的个体,淘汰部分较差的个体.这里选择比较成熟的轮盘赌策略,它的基本思路是依据适应度值的大小,通过轮盘赌的方式进行随机选择,这样个体适应度值越大,则被选中的的概率越大,其基本步骤为:
(2)计算每个个体适应度与总适应度的比值,得到个体的入选概率pi=fi/F;
(3)将所有个体的入选概率拼成一个轮盘;
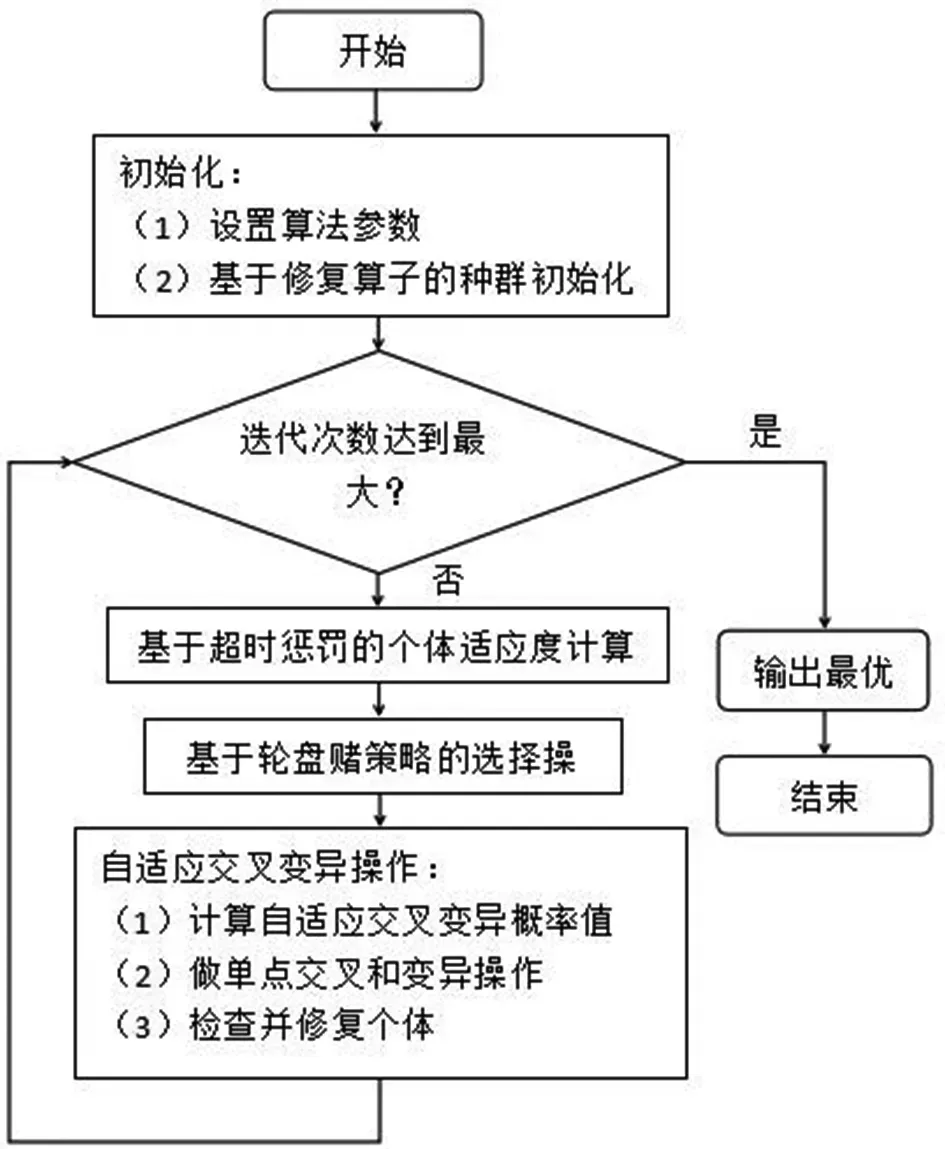
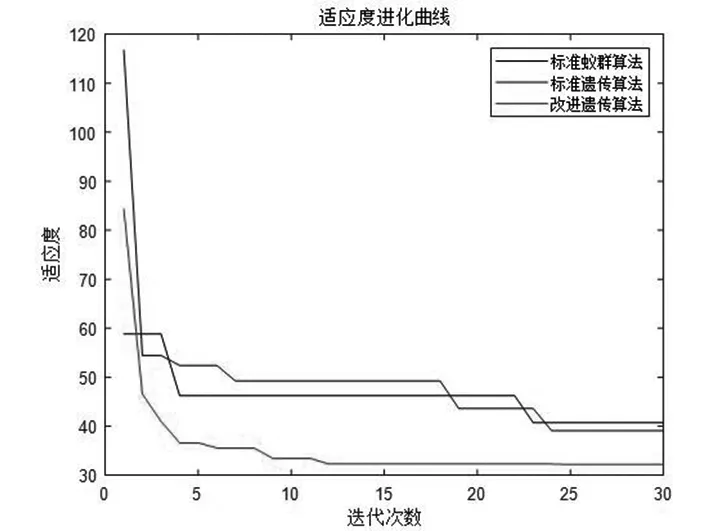
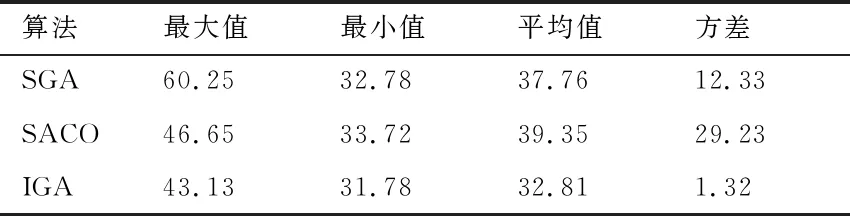
(4)转动轮盘,随机选择个体:随机生成一个[0,1]之间的数r,若pi≤r 遗传算法的选择操作只能将种群较优的个体筛选出来,遗传到子代种群中,并没有新个体产生.为保持种群的多样性,避免陷入早熟,真正实现全局寻优,还必须借助交叉和变异操作,前者是将种群中某两个个体的部分基因进行随机互换,后者是将某个个体的部分基因产生随机突变,因此两种操作本质上都产生了新个体,增强了种群的多样性.遗传算法的交叉和变异操作除了选取合适的交叉变异方式外,还需要设置交叉概率值和变异概率值,其中后者对算法进行全局寻优效果的影响也是非常明显的.为此,本文着重对交叉概率值和变异概率值的设置进行改进,采取自适应策略,使交叉和变异概率值能随着个体的平均适应度而改变,而不是取固定的取值. 设fi为某个个体的适应度值,favg为个体适应度值的平均值,fmin为个体适应度的最小值,由于外卖配送路径规划问题是极小值问题,这里将它们取倒数,记为: (8) 又设交叉概率值的范围为[pc1,pc2],变异概率值的范围为[pm1,pm2],自适应变化的交叉概率值和变异概率值记为pc和pm,则构造自适应变化公式如下: (9) (10) 其中α称为自适应增量因子,其公式为: (11) 根据式子(9)(10)(11),自适应交叉与变异概率值变化规律如图1图2所示: 由于外卖配送路径既包含商家节点,又包含客户节点,一旦个体的某个基因发生变异,则需要再次调用个体修复算子,检查并修复个体中异常的基因,使其成为合法个体(可行路径).为此,本文采用单点交叉和单点变异操作,一旦发生交叉或变异操作,必定会产生新的个体,在自适应交叉和变异概率控制下,能根据迭代进度保持合适的种群多样性,使收敛效果更好. 以某城市某区域的外卖配送情况为例[7],取某个外卖配送员的一次订单,如表1所示. 表1 外卖订单详情 表1中,同一行的商家和客户构成一组配送关系.外卖公司的配送中心编号为0,地址为(1.02,5.56). 外卖配送人员的平均行驶速度为v=200m/min,根据公式(1)计算出外卖配送员在两点之间行驶所需的时间,如表2所示.其中任意两点之间的距离以欧式距离公式来计算. 表2 各点之间的行驶时间(分钟) 按图3算法流程编写改进遗传算法(IGA)程序.为便于比较,同时还按照标准遗传算法(SGA)和标准蚁群算法(SACO)进行编程求解,其中蚁群算法是基于蚂蚁觅食行为和过程的仿生学智能算法,在求解路径规划类问题时也有良好的效果.三种算法的参数设置及求解结果如表3所示. 图3 改进遗传算法的流程图 表3 三种算法的参数设置及求解结果 从表3可以看到,种群规模与迭代次数均相同时,改进遗传算法(IGA)得到的最优适应度值均明显优于其余两种算法.所求得的最优路径为0→5→3→6→1→2→9→4→7→12→8→11→10→0.对应于表3,三种算法求解时的适应度进化曲线如图4所示. 图4 三种算法的适应度进化曲线 由图4可知,本文的改进遗传算法(IGA)由于采用了自适应交叉变异策略,大大增加了子代种群的多样性,加快了算法的收敛速度,迭代次数约15次时,适应度值已经趋于最优,表现出具有更强的寻优能力和收敛性. 为进一步测试本文改进遗传算法(IGA)的性能,将三种算法程序在MATLAB2016b环境中独立运行100次,各算法的参数仍按表3进行设置.记录并统计各个算法程序100次求解所得的最大值、最小值、平均值、方差,结果如表4所示. 表4 三种算法独立运行100次的统计结果 从表4可以看到,本文改进遗传算法(IGA)所求得最优值的平均值明显优于另外两种算法,最大值和最小值偏离均值的幅度也更小,对应的方差更是远小于另外两种算法.由此可见,本文改进遗传算法在修复算子和自适应策略的共同作用下,获得最优解的收敛速度更快、效率更高,求解过程更加稳定. 针对带时间窗的外卖路径规划问题,在标准遗传算法的基础上,将取值固定的交叉变异概率值改进为具有余弦变化特征的自适应概率值,进而提出改进遗传算法.仿真实例结果表明,改进遗传算法比标准遗传算法、标准蚁群算法的求解效率更高、求解结果更加稳定,算法的鲁棒性也更强.2.5 自适应交叉与变异策略
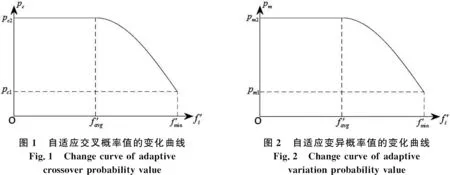
2.6 算法流程图
3 实验仿真与分析
3.1 数据准备
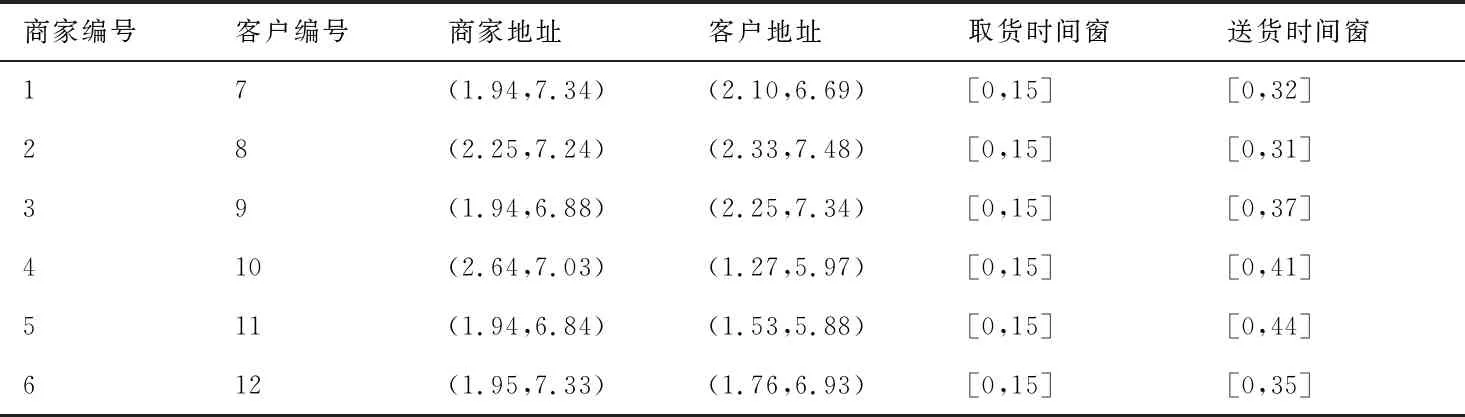
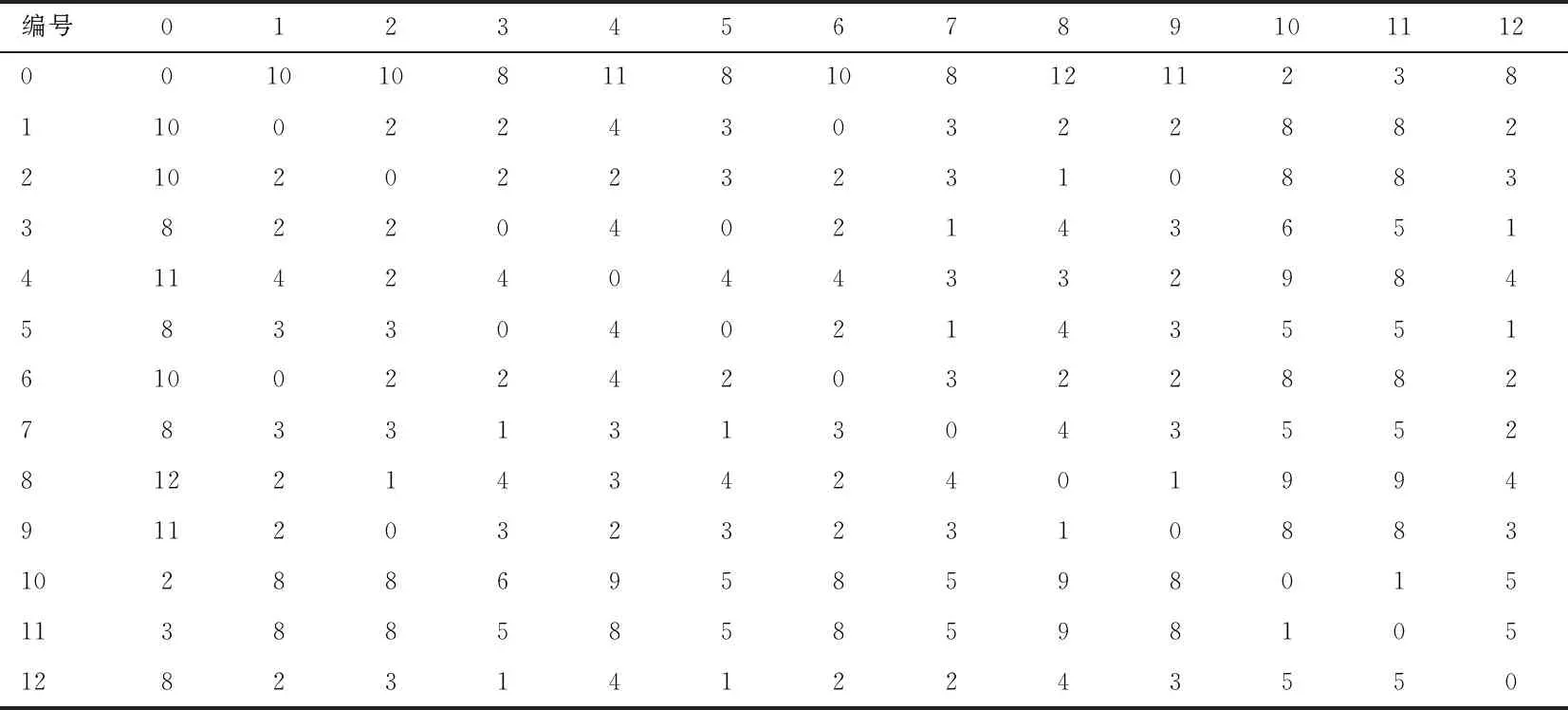
3.2 实验结果及比较

3.3 算法性能分析
4 结束语
