基于浮标44013数据的有效波高预测研究

邓泽贵，李醒飞，杨少波

(1.天津大学精密测量技术与仪器国家重点实验室，天津 300072；2.青岛海洋科学与技术试点国家实验室，山东 青岛 266003；3.天津大学青岛海洋技术研究院，山东 青岛 266200)

引 言

海洋是一座巨大的资源宝库，海洋覆盖面积占了全球表面积的70.8%。为了加强对海洋的利用，我们需要对海洋环境进行准确的分析、模拟和预报。海浪是最重要的海洋环境之一，有效波高是其主要的衡量参数，因此对海浪的分析我们可以从一定程度上转化为对有效波高(SWH, Significant Wave Height)的分析。精准的有效波高预测不仅能为海洋工程和航行提供重要的海洋气象参考条件，还能减少海洋环境对军事作战造成的影响。例如海浪在潜艇工作时就直接影响着潜艇近水面的稳定性，巨大的海浪对其他军事设备甚至航母的稳定性也有着一定的影响。从能源角度来看，随着化石能源的快速消耗，可再生能源成为了全人类关注的焦点。波浪能作为一种清洁并且分布广泛的可再生能源，相比于太阳能和风能拥有更高的可预测性和更高的能量密度，对其进行有效利用与开发具有的巨大商业价值和环境价值[1]。并且波浪能与有效波高的平方成正比，因此精准的有效波高预测可以为波浪能的有效利用与转化提供重要参考依据。

由于受到复杂海洋环境和自然混沌现象的影响，有效波高的精准预测极为困难。目前国内对有效波高预测的研究还较少，国外在上世纪就已经开始有效波高的预测研究。对于有效波高的预测可以分为两大类，分别是基于能量平衡方程的数值海浪模型和以数据作为研究对象的数据驱动模型。例如第一个业务化海浪预测的模型Wave Model(WAM)，适用于近海岸模拟的Simulating Waves Nearshore (SWAN)，基于WAM的WAVEWATCH III都是基于能量平衡方程的[2-4]。这类模型由于复杂的输入与物理模型本身的复杂度，其运行速度极慢。在这种情况下，经典时间序列模型自回归模型(AR, Autoregressive Model)、移动自回归模型(ARMA, Autoregressive moving average model)、差分整合移动平均自回归模型(ARIMA, Autoregressive Integrated Moving Average model)分别被Soares C G、Fusco F、Ge M等人应用到有效波高的预测中[5-7]。近年来，随着机器学习的蓬勃发展，许多机器学习模型被应用到有效波高的预测中。Deo M C和Makarynskyy O都研究了神经网络(ANN, Artificial Neural networks)在有效波高上的预测性能[8-9]。Cornejo-Bueno L采用遗传算法(GA, Genetic Algorithm)结合极限学习机(ELM, Extreme Learning Machine)来预测有效波高[10]。Kumar N K提出了多个ELM集成的方式预测有效波高[11]。Mahjoobi J将风速和有效波高作为支持向量机(SVM, Support Vector Machine)的输入来预测有效波高[12]。Elbisy M S提出支持向量机(SVM)结合遗传算法(GA)的组合模型来预测有效波高[13]。Salcedo-Sanz S使用了支持向量回归(SVR, Support Vector Regression)来预测有效波高[14]。模糊K近邻算法被Nikoo M R用来预测广阔湖面的有效波高[15]。

然而目前的有效波高预测研究都是基于不同的数据集，无法合理地评估各种模型的预测性能。为了准确地评估机器学习模型在有效波波高预测中的表现，本文研究了线性回归(LR, Linear Regression)，支持向量回归(SVR)，神经网络(ANN)，K近邻(KNN, k-Nearest Neighbor)，决策树(DT, Decision Tree)，随机森林(RF, Random Forest)六种经典机器学习模型在同一个数据集上的预测性能。同时本文的研究对以后有效波高预测模型及其驱动数据的选择提供了一定的参考。本文的安排如下：在第一部分介绍有效波高预测的意义以及相关论文的回顾；第二部分简单地介绍了六种模型的主要思想并分析了原始数据；第三部分进行了相关实验对比；第四部分对本文进行了总结。

1 模型与数据

1.1 机器学习模型

线性回归(LR)可由公式(1)表示，其中w=(w1,w2,...,wn)，b表示截距项，x表示输入特征向量，w和b学得之后，模型就确定了。一般通过最小化模型在给定数据集上预测的均方误差求解w和b。支持向量回归公式与线性回归类似，但支持向量机是通过间隔最大化思想来求解参数，并且可以通过引入核函数的方法使模型具有非线性能力。神经网络几乎可以拟合任何线性和非线性函数，对于只有一个隐藏层神经网络，它的前向传播表达式如(2)所示，其中x为输入特征向量；w1、w2为权重矩阵；b1、b2为偏置；h为隐藏层节点；y′为神经网络输出结果；σ(·)表示激活函数。其优化目标可以自己定义，一般通过梯度下降法来求解权重矩阵和偏置。K近邻是一种无参数学习的算法，被认为是“懒惰学习”的著名代表。K近邻算法的思想很简单，当一个新的样本需要预测时，我们只需要在给定数据集中找出K个离它最近的样本，然后将这K个样本标签的平均值作为新样本的预测值。决策树是一种常见的机器学习算法，它以树为基础结构，通过对一系列特征的连续判断来得到结果。随机森林则是以决策树为基学习器的集成学习模型，通过学习出m个子决策树，最终以这m个子决策树预测值的加权作为最终输出[16-17]。

f(x)=wx+b

(1)

(2)

1.2 数据

用于有效波高分析的数据通常来源于浮标实测数据，卫星高度计数据或再分析数据。其中浮标数据较为准确数据，但浮标数量有限，难以提供完整的区域数据。卫星高度计数据和再分析数据虽然能提供完整的区域数据，但准确率稍低。由于本文研究的是单点有效波高预测，所以我们选择了美国National Data Buoy Center (https://www.ndbc.noaa.gov) 公开的浮标数据。其中浮标44013提供每小时的标准气象数据，并且数据较为完整，因此我们选用此浮标2013年到2018年的数据作为我们的驱动数据。其中选取的数据包括风速、有效波高、主导波周期、平均波周期、水温五项参数。浮标44013的位置信息、水深及有效波高数据的最小值、最大值、平均值、方差如表1所示。

表1 浮标44013的统计信息

图1是编号为44013的浮标2013年到2018年有效波高曲线图。从图1可以看到，有效波高具有明显的年周期性，并且每一年有效波高呈现出一定的季节特性，在春、冬两季有效波高数值较大且变化剧烈，相比之下在夏、秋两季有效波高数值较小且变化平稳。为了充分利用浮标44013的数据来准确评估第二节的六种机器学习模型的预测性能，本文设计了三部分实验：第一部分实验以月为单位研究了未来一小时的有效波高预测；第二部分实验以季节为单位研究了未来一天的日平均有效波高的预测；第三部分实验以季节为单位研究了未来一天的日最大有效波高的预测。

图1 浮标44013 2013年到2018的有效波高曲线图

2 实验

(3)

(4)

(5)

(6)

(7)

(8)

2.1 实验1：提前一小时有效波高预测

在本文实验中所有模型都以历史数据作为输入。从图1的有效波高图可以看出有效波高存在一定年周期性与季节性。因此这部分实验使用2013到2018年春、夏、秋、冬的3、6、9、12月的数据作为模型驱动数据，其中2013年到2017年的数据作为训练集，2018年的数据作为测试集，最终评估经过训练的模型在测试集上的表现。并且在这部分实验中还对比了仅使用历史有效波高数据和使用历史风速、有效波高、主导波周期、平均波周期、水温五项参数作为模型输入的预测结果，在接下来内容中简称为单特征和多特征。由于模型的预测性能与模型参数有关，因此模型的主要参数都在附录中给出。

在仅使用单特征的有效波高预测中，以2013年到2017年每年3月有效波高数据作为训练集，以2018年3月份数据作为测试集，并且采取历史24小时有效波高预测未来一小时有效波高的方式。在使用多特征预测未来一小时有效波高时，本文研究了模型在风速、有效波高、主导波周期、平均波周期、水温五种特征下的预测性能，且采用历史12小时五项参数预测未来一小时有效波高。实验结果如表2所示，其中括号内的百分数表示模型在各个指标上相对于持续性预测的提升，粗体的数字表示各个评价指标的最优值。可以明显看出LR、SVR、ANN三种模型的在各项指标上面都优于KNN、DT、RF三种模型。其中ANN模型表现最好，在使用多特征时，其MAE、MAPE、RMSE分别仅为0.1354、0.0681、0.2059 m，R2指标达到了0.9840。并且相对于持续性预测法，ANN模型的MAE、MAPE、RMSE指标提升均超过了10%。相比之下，KNN、DT、RF三种模型的表现甚至不如持续性预测法。其中KNN算法的各项评估指标最差，其MAE、MAPE、RMSE分别为0.3758、0.2137、0.5759 m，而R2仅为0.8750。通过比较各模型在使用单特征和多特征时的预测结果可以发现，在使用多特征后，除KNN和DT外的四种模型基本都取得了更可靠的预测结果。表3展示了六种模型的训练时间，可以看到LR、KNN两组模型的训练时间最短且小于0.1 s，而ANN的训练时间最长，在使用多特征时达到了54.74 s。在使用单特征时，SVR的训练时间仅为0.24 s，而在使用多特征时，SVR的训练时间为25.27 s，增加了大约100倍。

表2 LR、SVR、ANN、KNN、DT、RF六种模型提前一小时有效波高预测结果及其相对提升-2018年3月

表3 LR、SVR、ANN、KNN、DT、RF六种模型的训练时间

图2展示了六种机器学习模型仅使用单特征时在 2018年3月的有效波高观测值与预测值，其中观测值以散点表示，预测值以曲线形式表示。同样可以看出LR、SVR、ANN三种模型的预测值曲线非常接近观测值，其中ANN模型的预测值曲线很好地拟合了几个极端的观测值。相比之下KNN、DT、RF三种模型的预测值曲线在一定程度上偏离了观测值散点，尤其是在第一个峰值附近，KNN、DT、RF三种模型都给出了一个较低的预测值，其中KNN算法的预测曲线相比于观测值在大多数时候都存在明显偏离。图3给出了多特征条件下六种模型在2018年3月预测值与真实值散点图，同样可看到LR、SVR、ANN三种模型的散点图比较接近理想拟合直线，而KNN模型的散点图偏离理想拟合直线最大，其拟合斜率仅为0.8785。

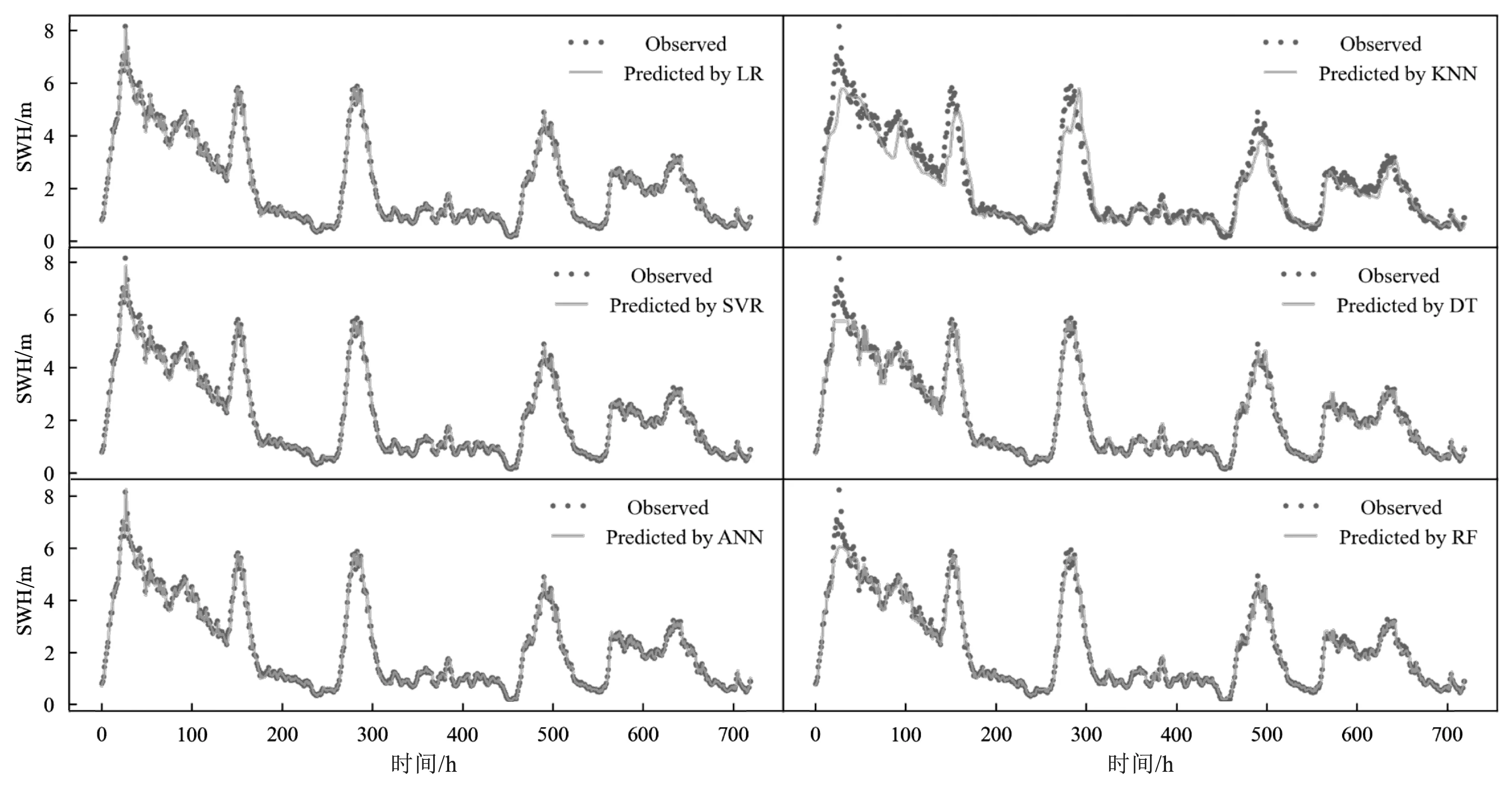
图2 2018年3月有效波高的观测值和预测值曲线

图3 使用多特征时六种模型在2018年3月的有效波高观测值与预测值散点图

为了研究季节对模型性能的影响，我们还对比了机器学习模型在2018年6月、9月、12月的有效波高预测性能。与2018年3月份有效波高预测类似，模型在2018年6月、9月、12月的预测结果如表4所示。从表4可以看到，LR、SVR、ANN三种模型的预测性能表现仍然明显好于KNN、DT、RF三种模型。其中ANN和LR模型表现较为稳定，相比于持续性预测法在各项指标上面均有明显提升，而SVR模型在MAE和MAPE指标上面出现了不同的下降。KNN、DT、RF三种模型的预测指标总体来说不如持续性预测法，仅RF模型在使用多特征预测2018年12月份有效波高时优于持续性预测法。通过比较模型在使用单特征和多特征时的预测结果可以看到，LR、SVR、ANN、RF四种模型使用多特征作为模型输入后都能减少模型的预测误差。在6月、9月、12月的有效波高预测中，所有模型对于6月的预测误差最低。其中ANN模型在使用多特征预测2018年6月有效波高时的MAE、RMSE分别仅为0.0433 m和0.0647 m。

表4 LR、SVR、ANN、KNN、DT、RF六种模型提前一小时有效波高预测结果及其相对提升-2018年6月、9月、12月

2.2 实验2：提前一天日平均有效波高预测

日平均有效波高同样也是海浪参数的一种重要表现形式，因此这部分实验研究了机器学习模型在日平均有效波高上的预测性能。相比每小时有效波高，日平均有效波高的时间分辨率变成了一天，因此其预测难度更大。并且从上一部分的实验可以看到使用多特征通常会提高模型预测准确率。为了降低日平均有效波高的预测误差，这部分实验都采用多特征来预测日平均有效波高。对于日平均有效波高的预测，我们以季节为单位来评估各模型的预测性能。以2013年到2017年的数据作为训练集，2018年春、夏、秋、冬四个季节的数据作为测试集。由于原始数据的时间分辨率为小时，因此我们对每天24小时的数据进行平均得到日平均数据。以前6天风速、有效波高、主导波周期、平均波周期、水温的日平均数据加上前24小时有效波高作为模型的输入，以未来一天日平均有效波高作为模型输出进行训练与测试，主要以三种误差指标及其相对提升百分比作为评判标准。

通过实验得到模型在2018年春、夏、秋、冬的预测结果如表5所示。可以看到SVR、ANN、RF三种模型的表现较好，LR和DT两组模型表现一般，KNN模型仍然表现最差。在预测2018年夏季日平均有效波高时，SVR的MAE、MAPE、RMSE的三种指标最好，分别是0.1770、0.2620、0.2862 m。在预测2018年秋季日平均有效波高时，ANN的MAE、MAPE、RMSE的三种指标最好，分别是0.1340、0.1959、0.2184 m。从各模型相对于持续性预测法在各个指标的提升上来看，ANN在三种指标上面都获得了稳定的提升。而SVR和RF模型的MAPE指标在秋季都出现了下降，分别下降了3.02%和14.64%。从各模型在四个季节的预测结果来看，模型在春、冬两季的预测结果明显差于夏、秋两季的预测结果。但在各模型在春、冬两季的相对提升百分比要远大于夏、秋两季。可以看到，在春季和冬季时KNN、DT、RF三种模型都好于持续性预测法。图4展示了六种模型在2018年春季的日平均有效波高预测值与真实值曲线，可以看到除KNN外的五种模型基本都把握住了日平均有效波高的变化趋势。在日平均有效波高较大的时刻，LR和SVR模型给出了一个较大的预测值，而ANN和DT模型则是给出了一个较为保守的预测值。

图4 六种模型在2018年春季的日平均有效波高观测值与预测值曲线图

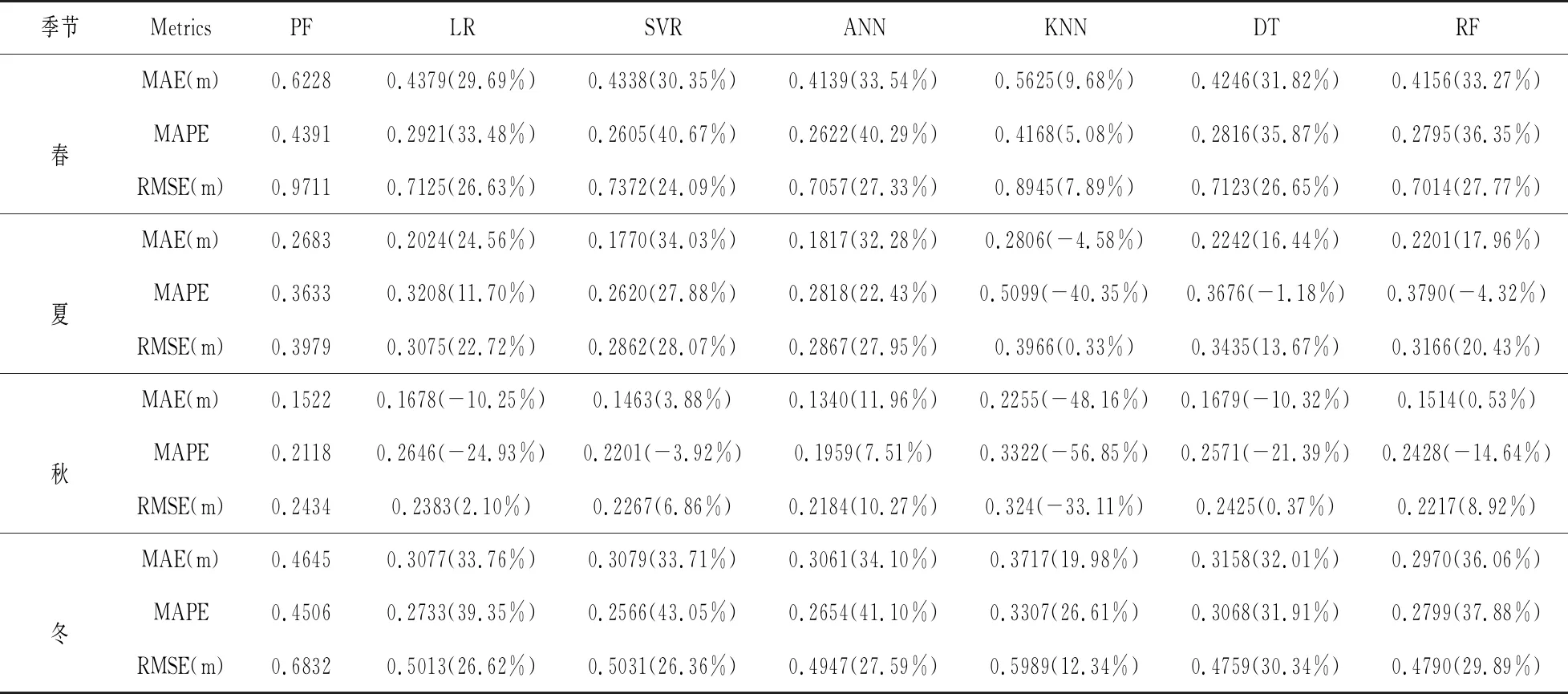
表5 LR、SVR、ANN、KNN、DT、RF六种模型提前一天日平均有效波高预测结果及其相对提升-2018年春、夏、秋、冬

2.3 实验3：提前一天日最大有效波高预测

在海洋中，日最大有效波高与人员安全，设备可靠性紧密相关。因此这部分实验研究了机器学习模型在日平均有效波高上的预测性能。与日平均有效波高相比，日最大有效波高属于极端值，其预测难度更大。对于日最大有效波高的预测，我们同样以季节为单位来评估各模型的预测性能。以2013年到2017年的数据作为训练集，2018年春、夏、秋、冬四个季节的数据作为测试集。以前6天风速、有效波高、主导波周期、平均波周期、水温的日最大值加上前24小时有效波高作为模型的输入，以未来一天日最大有效波高作为模型输出进行训练与测试。表6列出了模型的日最大有效波高预测性能，可以明显的看到，ANN模型的预测性能最好，SVR和RF两种模型表现一般，LR、DT、KNN三种模型表现较差。并且季节对模型预测能力的影响仍然存在，在夏季和秋季模型的预测误差都比春季和冬季低。这是因为在春季和冬季有效波高相对较大且变化更为剧烈，在这种情况下模型很难学习到一个普遍适用于所有时刻的规律。在预测2018年秋季日最大有效波高时，ANN模型的MAE和MAPE指标最低，仅为0.1973 m和0.2117 m；RF模型RMSE指标最低，仅为0.3302 m。从相对提升指标来看，ANN和SVR模型能够获得稳定的提升，而KNN和LR模型则在多个指标上出现了下降。图5展示了六种模型在2018年春季的日最大有效波高预测值与真实值曲线，可以看到KNN和DT两种模型的预测值和真实值曲线偏离较大。相比之下SVR、ANN、RF模型基本能够预测到日最大有效波高的变化趋势。

图5 六种模型在2018年春季的日最大有效波高观测值与预测值曲线图

表6 LR、SVR、ANN、KNN、DT、RF六种模型提前一天日平均有效波高预测结果及其相对提升-2018年春、夏、秋、冬

3 结论与展望

作为海浪的关键参数，有效波高在波浪能利用，海事活动规划，海洋探索等方面扮演着重要角色。准确的有效波高不仅可以促进波浪能的有效利用，还能为海洋活动提供重要的气象参考依据。本文研究了LR、SVR、ANN、KNN、DT、RF六种机器学习模型对于有效波高的预测表现，实验分为提前一小时有效波高预测、提前一天日平均有效波高预测和提前一天日最大有效波高预测三部分。从实验结果来看：

(1) 在预测未来一小时有效波高时，LR、SVR、ANN三种模型都能取得较好的预测指标，相对于持续性预测法基本都能取得明显提升，其中ANN的四种预测指标普遍是最优的。而KNN、DT、RF三种模型的表现较差，甚至不如持续性预测法，其中KNN表现极差。在使用多特征后，除KNN和DT外的四种模型都能取得明显的提升。

(2) 在预测未来一天日平均有效波高时，SVR、ANN、RF三种模型表现较好且差距不明显。在夏季时SVR模型的各项指标是最优的，在秋季时ANN的各项指标是优的，在冬季时RF模型的MAE和RMSE指标最好。相比之下，KNN模型表现仍然最差，预测值与观测值存在较大偏差。在预测未来一天日最大有效波高时，ANN模型在大多数时候都取得了最优的预测指标，SVR和RF次之，LR、KNN、DT三种模型表现较差。并且SVR和ANN模型相对于持续性预测法都有着稳定的提升，而RF模型仅在春冬两季提升比较明显。

(3) 在时间耗费上，LR和KNN两中模型由于其结构简单训练速度极快，都低于0.1 s。而ANN作为一个相对复杂的模型，其训练时间最长，达到了几十秒。在输入维度增加时，SVR的训练时间会急速增加，而其余模型的训练时间增长平缓。

(4) 从所有实验来看，在春冬两季模型的预测误差都大于夏秋两季，但相对于持续性预测法的提升在春冬两季更为明显。并且在所有实验中，多DT集成的RF模型明显优于单一的DT模型。在三种预测任务中，未来一小时有效波高预测误差最低，未来一天日最大有效波高预测误差最大。

综上，在预测未来一小时有效波高时，LR和SVR训练速度快且结果较好，ANN则拥有稍好的预测准确率。在日平均有效波高预测中SVR、ANN、RF都能提供相对可靠的稳定结果，其中RF速度最快。在日最大有效波高预测时，ANN总是优于 SVR、RF，但三种模型差距不大。总体来看，ANN是最稳定的模型，通常都能获得最优的预测指标，而KNN和DT都不是最优的选择。因此在以后基于机器学习的有效波高预测中，模型的选择起着至关重要的作用。在本文实验中，模型输入都只选用了单点气象数据，而没有考虑目标点周围的影响，考虑空间相关性的有效波高预测将是接下的一个重要研究方向。多模型集成的方式可以在一定程度上提高有效波高预测的精准度。另外本文研究的都是单模型的预测性能，要想提升模型预测有效波高的精准度可以结合一些其他技术，例如促进参数寻优的遗传算法、粒子群算法等；分解原始有效波高序列的小波变换、经验模态分解等。