工程教育认证背景下结构力学“金课”设计研究

咸庆军 张庆章 金立兵 陈俊旗

摘要：本文基于工程教育理念，针对结构力学课程特点，分析了结构力学课程对土木工程专业毕业要求的支撑作用，按照“金课”标准对结构力学教学思路进行设计。以力法求解超静定结构的课程内容为例，采用案例教学法、启发式教学法、研讨式教学法等多种方法，从工程实例引入超静定结构，讨论力法求解的具体思路和步骤，并应用于解决郑州奥体中心体育场钢结构工程等问题，实现从解决一般工程问题到解决复杂工程问题的跨越。课程教学取得了良好成效，可为其他工科工程基础类课程教学提供参考。

关键词：工程教育理念;“金课”;力法;案例教学法;复杂工程问题

中图分类号：G642.3;TU4   文献标志码：A   文章编号：1005-2909（2022）01-0113-10

一、结构力学课程对毕业要求的支撑作用

1989年，《华盛顿协议》（Washington Accord，简称WA）由美国、英国、加拿大等6个国家发起和签署，是工程教育本科专业学位互认协议，其宗旨是通过多边认可工程教育资格，促进工程学位互认和工程技术人员的国际流动。《华盛顿协议》是国际工程师互认体系中最具权威性、国际化程度较高、体系较为完整的协议。2013年，中国加入《华盛顿协议》，成为预备成员。2016年，中国成为《华盛顿协议》第18个正式成员，这就意味着中国高等工程教育必须按照协议要求做好工程教育专业认证工作，按照实质等效的原则培养学生[1]。

2018年，河南工业大学土木工程专业顺利复评通过中国工程教育专业认证，工程教育专业认证通用标准的核心理念是学生中心、成果导向、持续改进[2-3]。学生毕业时所达到的毕业要求，以及毕业后一段时间（5年左右）达到的培养目标，集中反映了工程教育的成果。课程体系、师资队伍和支持条件等教学资源对毕业要求的支撑作用，以及毕业要求对培养目标的支撑作用，集中体现了“成果导向”理念，并在此过程中不断进行“持续改进”。其中，毕业要求是对学生毕业时应该掌握的知识和能力的具体描述，包括学生通过本专业学习所掌握的知识、技能和素养，也是本科毕业生步入职业岗位时所必须具备的能力。根据我校土木工程专业培养目标，结合工程教育专业认证通用标准和本专业补充标准，制定了11项毕业要求，除毕业要求9对应通用标准毕业要求9、10外，其他毕业要求都一一对应，完全覆盖工程教育认证标准中的12项毕业要求（工程知识、问题分析、设计/开发解决方案、研究、使用现代工具、工程与社会、环境和可持续发展、职业规范、个人和团队、沟通、项目管理、终身学习）。

通过对11项毕业要求分析发现，1—5属于技术性的，6—11属于非技术性的。此外，1—7和9中均含有“复杂工程问题”，说明这8项毕业要求都与解决“复杂工程问题”有关[4]。这8项毕业要求分别涉及解决“复杂工程问题”所需的多学科知识、分析方法、解决方案、研究方法、技术和工具、社会责任意识、环境与可持续发展意识以及沟通交流能力等。其中1、6、7、9是解决“复杂工程问题”所需的知识和素养;2、4、5是“复杂工程问题”分析与研究的方法;3提供了“复杂工程问题”的系统解决方案。8项毕业要求是系统性的要求，彼此相互联系。可见，“复杂工程问题”不仅是工程技术问题，还涉及大量非技术性问题，充分说明了解决“复杂工程问题”的能力是毕业要求的核心内容，是工程教育的主要目标，也即是《华盛顿协议》的实质核心。

结构力学课程属于工程基础类课程模块，该模块在培养解决复杂工程问题能力方面表现为：能够应用多学科知识及其基本原理，选择与使用恰当的现代工具，系统深入地识别、表达、研究、分析和解决复杂工程问题。如表1所示，结构力学课程对应毕业要求1、2、5及其相应的5个指标点。由此可见，结构力学课程所支撑的毕业要求与其所属课程模块的功能相吻合。畢业要求1、2、5均属于技术性的，都与解决复杂工程问题有关。结构力学课程对毕业要求的支撑作用体现在：从技术角度运用土木工程等多学科知识及其基本原理，借助现代工具，建立合理的预测模型，分析与解决土木工程专业的复杂工程问题。

二、结构力学“金课”设计思路

（一）“金课”的提出

2018年6月21日，教育部部长陈宝生在新时代全国高等学校本科教育工作会议上提出，大学生要有效“增负”，提升大学生的学业挑战度，合理增加课程难度，拓展课程深度，扩大课程的可选择性，真正把“水课”变成有深度、有难度、有挑战度的“金课”。同年8月份，教育部在专门印发的《教育部关于狠抓新时代全国高等学校本科教育工作会议精神落实的通知》（教高函〔2018〕8号）[5]上提出，各高校要全面梳理各门课程的教学内容，淘汰“水课”、打造“金课”，合理提升学业挑战度、增加课程难度、拓展课程深度，切实提高课程教学质量[6]。

“金课”的标准可以归结为“两性一度”：高阶性、创新性和挑战度。高阶性即知识、能力、素质有机融合，培养学生解决复杂问题的综合能力和高级思维;创新性体现在课程内容反映前沿性和时代性，教学形式体现先进性和互动性，学习结果具有探究性和个性化;挑战度是指课程有一定难度，需要学生“跳一跳”才能够得着，对教师备课和学生课下有较高要求。其中，高阶性反映了“金课”的教学目标是培养学生解决复杂问题的综合能力和高级思维，这和结构力学课程对毕业要求的支撑作用“运用土木工程等多学科知识及其基本原理，分析与解决土木工程专业的复杂工程问题”是完全吻合的。这也说明教育部提出的“金课”标准与工程教育的目标是一致的。

（二）结构力学课程特点

结构力学是土木工程专业重要的基础课程，在整个课程体系中处于承上启下的核心地位。一方面以高等数学、理论力学、材料力学等课程为基础;另一方面是钢结构、混凝土结构及基础工程等专业课程的基础。结构力学作为一门力学课程，具有如下特点：课程抽象性、逻辑性、理论性较强;课程知识点多，计算画图多，前后联系，难度较大;课程算例来源缺少工程背景，理论知识与实际工程应用脱节等，导致学生学习兴趣不大、积极性不高，容易丧失学习动力。

（三）“金课”设计思路

课堂教学是“金课”的主阵地、主渠道、主战场[6-7]。针对结构力学的课程特点以及学生学习过程中出现的问题，践行工程教育理念并考虑结构力学课程对毕业要求的支撑作用，以课程内容“力法求解超静定桁架结构”为例，按照“金课”的标准对其教学思路设计如下。

1.从工程实例引入超静定桁架结构

以往超静定桁架结构算例来源缺少工程背景，为此需采用案例教学法，从实际工程中选取典型的超静定桁架结构，并与学生一起讨论其计算简图的简化过程，为后面的计算奠定基础。

2.力法求解超静定桁架结构的具体思路和步骤

结构力学课程向来理论性较强、难度较大，为此采用问题式及启发式教学法[8]，通过不断提出有启发性的问题引导学生深入思考与讨论，结合重点与难点问题边讲边练，使学生逐渐掌握力法求解超静定桁架结构的具体思路和步骤。

3.引导学生认识、思考并解决复杂工程问题

按照以上力法求解超静定桁架结构的教学方法和思路，进一步完成力法求解超静定刚架、排架和组合结构等教学内容，培养学生综合运用相关知识解决一般工程问题的能力。

在此基础上，针对结构力学理论知识与实际工程应用脱节的问题[9]，采用案例教学法[10]和研讨式教学法，以郑州奥林匹克体育中心体育场钢结构工程为例，把学生分为若干研究小组，小组成员通过课下查阅相关资料，综合运用多学科知识及其基本理论，形成有限元模型并撰写研究报告，并在课上进行汇报和讨论，从而培养学生认识、思考并解决复杂工程问题的能力。

三、从工程实例引入超静定桁架结构

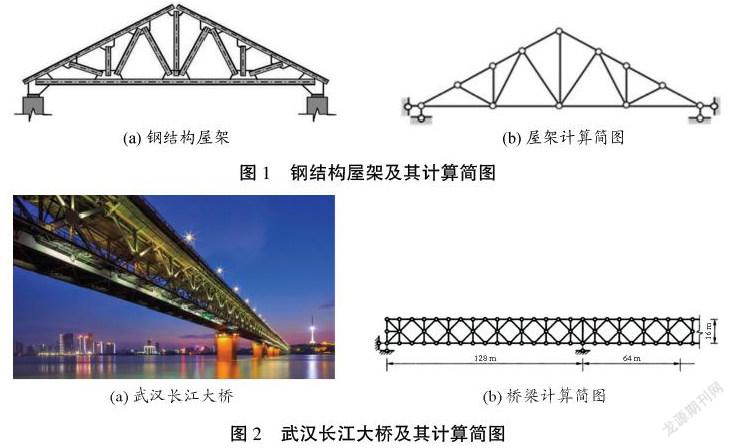
桁架结构的杆件内力只有轴力，杆件截面上应力分布均匀，可充分发挥材料强度，因而广泛应用于屋盖、桥梁、高层建筑以及体育场馆等实际工程中。采用案例教学法，图1所示为钢结构屋架，若屋架两端与柱顶连接牢固而不产生相对水平位移，则柱子对屋架的约束可作为固定铰支座，简化为一超静定桁架结构;图2所示为武汉长江大桥，桥梁类型为多跨连续桁架桥梁，虽然支座可看作是简支的，但中间支座处的竖向腹杆是多余约束，整个桥梁可简化为多次超静定桁架结构。

图1和图2所示的钢结构屋架和武汉长江大桥在简化得到相应计算简图的过程中，与学生讨论，需要注意以下问题。

（1）钢桁架结构中杆件之间连接形成的节点有几种不同的类型：直接相贯焊接节点、节点板焊接节点、焊接空心球节点、螺栓球连接节点以及铸钢连接节点等。这里屋架和桥梁的杆件之间采用节点板焊接节点，节点处杆件之间的相对转动受到一定的约束，节点并非理想铰结，但在超静定桁架结构计算简图中简化为理想铰结点。

（2）屋架和桥梁中的杆件设计为直杆，但在杆件制作、运输及安装過程中可能会产生一定的初弯曲，也就是杆件轴线不一定是理想直线，同时在杆件安装完成后，节点处各杆的轴线也不一定全部相交于一点。为了忽略这些因素的影响，在桁架结构计算简图中，认为各杆轴线都是直线，并且通过铰结点的中心。

（3）在屋架和桥梁结构的上弦杆上，上面的荷载并非正好作用在上弦杆的铰结点处，同时支座反力的作用点也不一定通过支座铰结点。为了反映桁架结构的主要受力特性，可把上弦分布荷载或其他类型荷载简化为作用在上弦铰结点处的集中荷载，并且认为支座反力作用在支座铰结点处。

综上所述，对屋架和桥梁结构进行受力分析时，可选取图1（b）和图2（b）所示的超静定桁架结构计算简图。

四、力法求解超静定桁架结构的具体思路和步骤

由于图1（b）和图2（b）所示的超静定桁架结构计算简图杆件较多，为便于计算，这里选取类似杆件较少的桁架结构为例，采用问题式和启发式教学法，讨论力法求解的具体思路和步骤。

（一）超静定桁架结构

所选取的超静定桁架结构如图3（a）所示，各杆材料相同，弹性模量为E，其中杆件②④⑥的截面面积为4A，杆件⑤的为5A，其余各杆均为3A，采用力法求解各杆轴力。

（二）基本体系选取

采用几何构造分析方法，通过去掉两个支座以及与之相连的两个二元体，余下杆件具有一个多余约束的几何不变体系，所以原结构为一次超静定结构。将中间一根链杆截断，加上相应的一对轴力X1作为多余未知力，即可得到如图3b所示的基本体系1。

通过提出“能否选用不同的基本体系”的问题，启发学生思考并练习选取不同基本体系的方法。以图3c为例，把上面一根水平链杆截断，同时加上一对轴力X1，作为基本体系2。根据学生练习和讨论的情况发现，对于中间由6根杆组成的杆件体系，不论截断哪一根杆件，都可以去掉一个约束，得到的结构均为静定结构，也就是说都可以作为基本体系进行计算。

（三）建立力法方程

对于图3（b）所示的基本体系1，根据变形协调条件，可以列出力法方程：δ11X1+Δ1P=0。

为了使学生理解力法方程的含义，进一步提出“力法方程等号两边各表示什么意思”的问题，通过讨论可知，方程左边表示基本体系1在未知力X1和结点荷载P共同作用下所产生的沿X1方向的相对轴向位移，而方程右边则表示原结构在结点荷载P作用下产生的沿X1方向的相对轴向位移为零。

最后，留下“如果考虑如图3（c）所示的基本体系2，那么力法方程的形式以及方程两边所表示的含义有无变化”的问题，进一步启发学生深入思考并理解力法方程的含义。

（四）计算系数和自由项

力法方程中的系数和自由项的表达式为： δ11=∑F-2N1lEA，Δ1P=F-N1FNPlEA。

借此与学生分析和讨论可知，系数δ11表示基本结构在单位未知力X1=1作用下产生的沿X1方向的相对轴向位移，而自由项Δ1P表示基本结构在结点荷载P作用下所产生的沿X1方向的相对轴向位移，即系数和自由项在本质上都是指静定桁架结构的位移，从而与前面静定结构位移计算的内容建立联系。

根据以上系数和自由项的表达式，需要计算基本结构在单位力作用下的各杆轴力F-N1，见图3（e），以及结点荷载作用下的各杆轴力FNP，见图3（d），从而计算得到δ11=1.51a/EA，Δ1P=-0.61Pa/EA。

对于基本体系2，要求学生练习计算F-N1和FNP以及相应的系数和自由项，并比较由此引起的计算量的不同。

（五）求解力法方程

对于基本体系1，在计算得到系数和自由项的基础上，求解得到X1=0.404P。而对于基本体系2，要求学生自行求解力法方程。

（六）计算各杆轴力

如何计算超静定桁架结构的各杆轴力呢？结合前面的求解过程讨论可知，当未知力X1求出后，图3（b）所示的基本体系1与图3（a）所示的原结构就完全等效了。而基本体系1在X1和P共同作用下的各杆轴力，可由公式进行FN=F-N1X1+FNP叠加计算得到，也就是原结构的各杆轴力，见图3（f）。

对于基本体系2，也要求学生通过叠加计算各杆轴力，并与上面的计算结果进行比较验证，从而选取一种计算量少、计算效率高的基本体系。

五、引导学生认识思考并解决复杂工程问题

按照以上教学方法，继续完成力法求解超静定刚架、排架和组合结构等教学内容。以此为基础，采用案例教学法和研讨式教学法，以郑州奥林匹克体育中心体育场钢结构工程为例，进一步培养学生认识思考并解决复杂工程问题的能力。

（一）体育场的三角形巨型桁架结构

如图4（a）所示，郑州奥林匹克体育中心工程位于郑州市常西湖新区，已于2019年6月竣工，作为2019年9月举行的中国第十一届少数民族传统体育运动会的主办场地。本工程主要包括“一场两馆”，由体育场、体育馆、游泳馆及商业房屋和地下室组成。如图4（b）、4（c）所示，郑州奥体中心体育场屋盖平面近似为圆形，南北向约291.5 m，东西向约311.6 m，看台罩棚南北向悬挑长度30.8 m，东西向悬挑长度54.1 m。体育场屋盖空间钢结构由4部分组成，分别为内罩棚大开口车辐式索承网格结构、外罩棚双层网架结构、南北端空中连廊三角形巨型桁架结构，以及外围立面桁架结构。

由于体育场空间钢结构形式新颖、组成复杂，如图5所示，这里选取典型的相对独立的三角形巨型桁架结构为例进行研究。三角形巨型桁架结构跨度82 m，支承于两端钢框筒上。三角形巨型桁架投影区域为圆环形，覆盖面积约2 092 m2，总周长25 m。三角形巨型桁架包括钢框筒、平面桁架、立面三角桁架3部分，部分连接采用焊接球节点。钢框筒柱底在混凝土结构标高6.7 m平台处，施工区域分为吊装区和提升区，其中钢框筒区域采用原位吊装施工方法，三角形巨型桁架區域采用整体提升施工方法。

（二）整体提升符合复杂工程问题的特征

由于三角形桁架跨度大、重量大、结构复杂，为了保证安装质量并提高安装效率，三角形巨型桁架采用整体提升施工方法。如表2所示，根据工程教育认证标准列出了复杂工程问题所具备的特征[3]。与力法求解低次超静定平面桁架结构相比，此三角形巨型桁架结构属于n次（n值很大）超静定大跨空间钢结构体系。如表3所示，经分析，三角形巨型桁架结构整体提升施工问题完全符合复杂工程问题特征[11]。

（三）教学设计及组织实施

1.教学设计

针对此复杂工程问题，需要对三角形巨型桁架结构的整体提升进行施工过程分析。通过把学生分为若干研究小组，小组成员课下查阅相关资料，运用多学科知识及其基本原理，采用有限元分析软件建立数值模型并进行计算分析，撰写研究报告，最后课上进行汇报和讨论。

2.组织实施

每个研究小组计划由3名成员组成，课下安排两周时间，其中1人查阅相关资料，1人建立数值模型，1人撰写研究报告，相互间协调配合。

（1）查阅相关资料

在掌握力法求解超静定结构等结构力学知识的基础上，进一步查阅钢结构、空间结构、建筑施工、土木工程试验、建筑结构软件应用等课程资料，结合三角形巨型桁架结构实例，掌握相关知识及其基本原理，为建立相应的数值模型做准备。此环节支撑表1所示的毕业要求1。

（2）建立数值模型

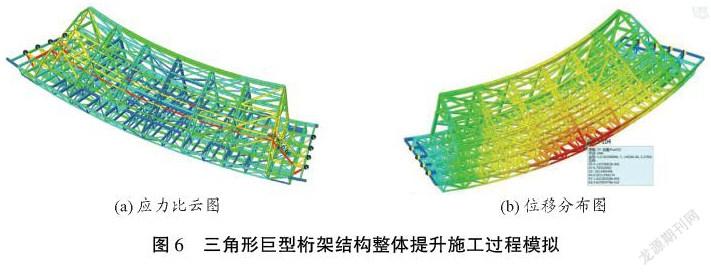
综合运用土木工程等多学科知识及其基本原理，选用ABAQUS、MIDAS等有限元分析软件，考虑到风荷载、补装构件、节点连接刚度、温度效应等多种因素的影响，建立符合工程实际的数值模型，对三角形巨型桁架结构进行整体提升施工过程模拟，如图6所示，并对计算分析结果的可靠性进行判定，为钢结构整体提升施工提供参考依据。此环节支撑表1所示的毕业要求2和5。

（3）撰写研究报告

根据所建数值模型以及计算分析结果，撰写相应的研究报告。内容涉及三角形巨型桁架结构实例介绍、几何模型简化及数值模型建立过程、数值模型可靠性验证、应力及位移计算结果分析、结构稳定性分析、多种因素影响分析、研究结论等。

（4）汇报和讨论

在课堂上，由撰写报告的学生代表本组汇报研究的过程及结果，其余2人进行必要的补充和完善，并负责回答其他学生和教师的提问。

在研究小组中，每名成员在完成自己任务的过程中，与其他成员相互协调配合。同时，本小组成员也能够就研究过程中遇到的各种问题与其他学生和教师进行有效沟通和交流，包括撰写研究报告、汇报和讨论等。因此，本部分内容除支撑表1所示的毕业要求1、2、5外，还能够支撑毕业要求9，也即对应通用标准毕业要求9“个人和团队”和10“沟通”。

六、结语

本文基于工程教育理念，按照“金课”的标准对结构力学教学进行设计，取得了良好成效，可为工科专业其他工程基础类课程的教学提供参考。

首先，本着结构力学知识“来源于工程，又服务于工程”的思想，通过从工程实例引入超静定桁架结构，进而讨论力法求解超静定桁架结构的思路和步骤，把所学知识应用于解决郑州奥体中心体育场钢结构工程问题，从而完成了从解决一般工程问题到解决复杂工程问题的跨越。通过理论与实践相结合，学生学习兴趣明显提高，积极性和主动性逐渐增强，学习动力和潜能也被激发出来。

其次，对照“金课”的标准“两性一度”进行分析。从高阶性来说，通过学习力法求解超静定结构的知识，逐渐培养学生解决复杂工程问题的能力和素质。从创新性来说，结合常见的屋架和桥梁以及典型的地标性建筑学习力法知识，课程内容反映了前沿性和时代性;教学过程中采用案例教学法、启发式教学法、研讨式教学法等多种方法，采用课下撰写报告、课上汇报和讨论的形式，教学形式体现了先进性和互动性;当选用不同基本体系时，力法求解过程及难易程度不同，不同研究小组所建数值模型及分析结果不同，表明了学习结果具有探究性和个性化。从挑战度来说，教师备课时需精心设计授课思路并选取典型的工程实例，学生课下需综合运用知识建立数值模型并撰写研究报告，都体现了课程的难度。

最后，在掌握力法求解超静定结构等结构力学知识的基础上，综合运用土木工程等多学科知识及其基本原理，选用合适的有限元分析软件，考虑各种因素的影响，建立符合工程实际的数值模型，对三角形巨型桁架结构进行整体提升施工过程分析，为钢结构整体提升施工提供参考依据，实现解决土木工程专业的复杂工程问题。

参考文献：

[1]陈聪诚.新中国高等工程教育改革发展历程与未来展望[J].中国高教研究，2019（12）：42-48，64.

[2]中国工程教育专业认证协会.工程教育认证标准（2017版）[S].2017.

[3]住房和城乡建设部高等教育土木工程专业评估委员会.全国高等学校土木工程专业评估（认证）文件（2017版·总第6版）[S].2017.

[4]韩婷，李红斌，文劲宇，等.培养复杂工程问题解决能力的一体化课程体系——华中科技大学电气工程及其自动化专业改革[J].高等工程教育研究，2018（2）：52-59.

[5]教育部.关于狠抓新时代全国高等学校本科教育工作会议精神落实的通知[EB/OL].（2018-08-22）[2018-08-27].http：//www.moe.gov.cn/srcsite/A08/s7056/201809/t20180903_347079.html？from=timeline.

[6]吴岩.建设中国“金课”[J].中国大学教学，2018（12）：4-9.

[7]许驰，陈庆章.课堂教学内容重构的原则与方法[J].高等工程教育研究，2018（4）：137-143，151.

[8]田社平，王力娟，邱意弘.问题式教学法对工科大学生批判性思维倾向影响的实证研究[J].高等工程教育研究，2018（6）：156-160.

[9]贾穗子，徐能雄.土木工程专业结构力学教学与工程实际结合的探讨[J].高等建筑教育，2018，27（4）：126-130.

[10]郑玉国.结构力学课程教学应重视工程直觉的培养[J].高等建筑教育，2016，25（1）：100-104.

[11]郑鲲，周晶，王卓峥.基于复杂工程的创新实践情境设计与评价[J].高等工程教育研究，2019（3）：170-174，194.

Abstract： Based on the concept of engineering education， supporting effect of structural mechanics to graduation requirements of civil engineering specialty is analyzed. In view of the course features of structural mechanics， teaching ideas of structural mechanics are designed in accordance with golden course standard. Take the course content of force method for solving statically indeterminate structure for example， methods such as case teaching method， heuristic teaching method， discussion teaching method and so on are adopted. First the statically indeterminate structure is introduced from project cases， then specific ideas and steps of solution with force method are discussed， finally the knowledge learned is applied to solve steel structure engineering problems of the stadium in Zhengzhou Olympic Sports Center， thus general engineering problems and complex engineering problems are all solved. The teaching process achieves good results， which provides references for teaching of other foundation engineering courses.

Key words： the concept of engineering education; golden course; force method; case teaching method; complex engineering problems

（責任编辑 崔守奎）