例谈用空间向量求解立体几何中距离问题的技巧

郭美玲

立体几何中的距离问题主要包括求点到平面的距离、直线到平面的距离、异面直线之间的距离、两个平面之间的距离.采用常规方法求解立体几何中的距离问题，往往要先根据题意和几何图形，确定点到平面的距离、直线到平面之间的距离、异面直线之间的距离、两个平面之间的距离；然后再利用勾股定理、两点间的距离公式、正余弦定理来进行计算.其思路较为繁琐，且很多同学经常找不到点、线、面之间的距离.对此，我们需运用向量法，通过构造空间向量和向量运算来求得空间距离.

一、求点到平面的距离

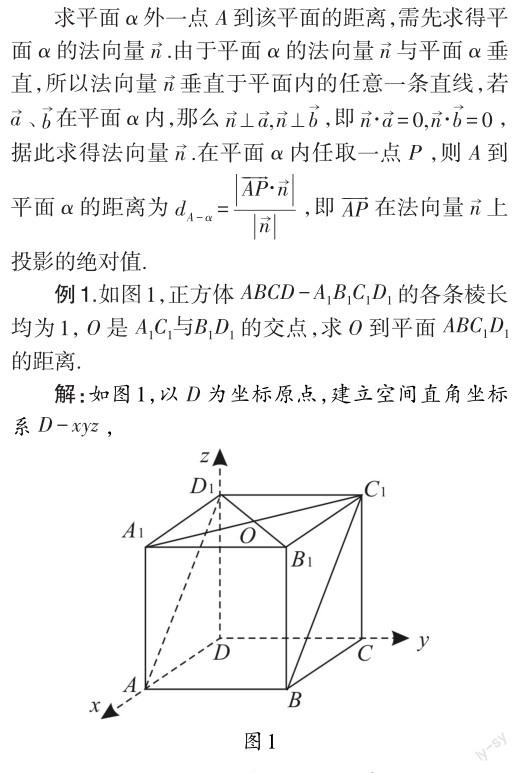
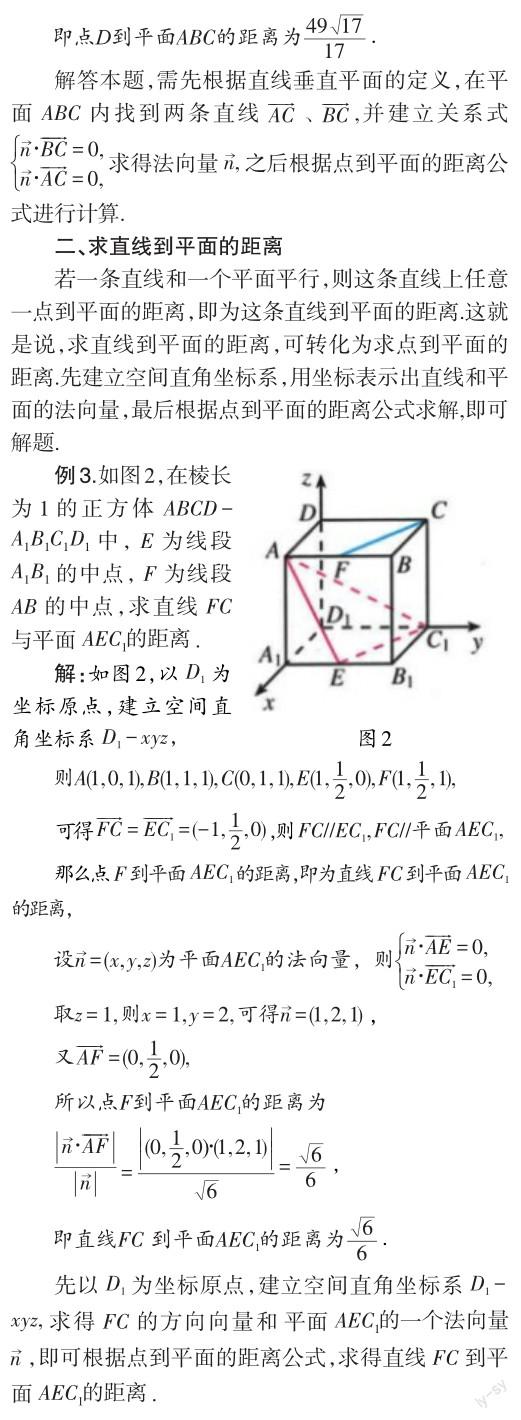
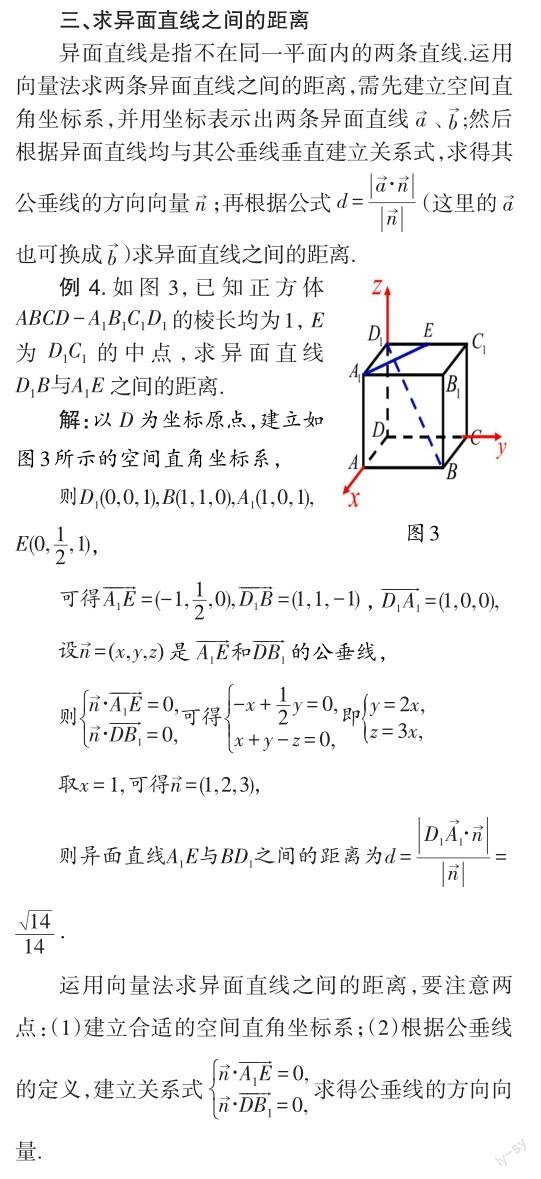
可見，运用空间向量来求立体几何中的距离，将问题转化为向量问题求解，能达到事半功倍的效果.用空间向量求立体几何中距离问题的基本思路为：（1）根据几何图形的特点，建立合适的空间直角坐标系；（2）把相关的点、直线、平面用向量表示出来；（3）根据点到平面的距离公式进行求解.

（作者单位：江苏省泗洪姜堰高级中学）