基于教学优化算法的帕金森疾病数据特征选择方法研究

郑金格,刘琳琳，翟梦鑫，李 昊

(1.周口师范学院 网络工程学院， 河南 周口 466001；2. 俄罗斯国立信息与无线电电子大学，白俄罗斯 明克斯 220002)

帕金森疾病(Parkinson’s disease，PD)是一种仅次于阿尔茨海默症常见的老年人神经系统变性疾病，最主要的病理改变是中脑黑质多巴胺(dopamin，DA)神经元的变性死亡。目前我国帕金森发病率为17%，大概有200多万帕金森病人，预计2030年将达到494万人[1]。该疾病会导致人体运动失调，进而影响人的正常生理活动，严重情况下，患者将无法正常行走、交谈。目前还没有治愈该疾病的方法，但准确的医疗诊断可帮助医生对患者进行早期干预，在一定程度上降低或延缓发病率。另一方面，PD诊断治疗费用十分昂贵，且诊断具有一定复杂性[2]。错误的诊断不仅会耗费大量资源，也会影响疾病治愈率。随着机器学习技术的不断发展，传统的医疗健康模式发生重大改变，通过机器学习进行辅助诊断逐渐成为热门。目前已积累了许多帕金森病人的疾病数据，如得到广泛使用的牛津大学Little等人收集的Speech PD数据，包含197条数据，23个属性特征[3]，Elli Valla等人收集的DraWritePD数据等[4]，把疾病数据通过特征选择方法进行处理，通过选取重要属性进行研究，帮助医生进行诊断，这对帕金森诊断具有重要意义。

特征选择是机器学习方法之一，是从现有特征子集中选择表现最好的特征子集。特征选择方法根据子集评估函数和后续的机器学习算法，可以分为过滤式(Filter)、封装式(Wrapper)和嵌入式(Embedded)[5]三种。 Filter方法首先是选取原始的数据集，然后再训练算法模型，这两个过程是相互独立的[6]。该方法的评价准则是使用统计学标准对各个特征进行评估，通过对分数进行排序。然而，这种方法单独看每个特征，而不考虑每个特征与后续环节中使用的模型之间的依赖性和相关性，这可能导致选择一个低分的特征子集。如移除低方差特征。Wrapper方法是与后续的机器学习算法结合使用，从而使算法能够实现高性能。将特征选择当作特征子集搜索，筛选出所有可能的特征子集，然后用分类器的性能评估特征的重要性[7]。相对于Filter方法，Wrapper方法考虑到了特征之间的相关性以及特征组合对模型性能的影响。如典型的递归删除算法(Recursive feature elimination，RFE)[8]，是一种寻找最佳特征子集的贪心算法，可以计算出所有的特征排名。Embedded方法是在选定模型的情况下，选出对模型训练有利的特征。先用Filter方法预选择特征，降低原始数据集的维度，之后用Wrapper方法选择最佳特征子集，找到各个特征的权重,然后根据模型的准确率与权重依次选择特征，Embedded相较于其他方法更为复杂。

近年来，基于Wrapper的特征选择方法相较于一般的Filter方法，医疗数据诊断性能更优，被越来越多的应用到医学诊断研究当中。如Rajalaxmi等人提出了基于Wrapper的二进制灰狼算法，并通过KNN进行分类[9]。Jisha Augustine等人基于血液的基因表达生物标志物使用两层混合特征选择的识别用于帕金森病的无创诊断，并通过逻辑回归进行分类预测[10]。Deepak Gupta等人通过优化墨鱼算法来确定最优子集，通过决策树和K近邻进行评估，准确率为94%，最大限度提高了准确性，减少了所选特征数目[11]。Zehra Karapinar Senturk通过回归树、人工神经网络、支持向量机对帕金森语音数据进行分类预测，准确率达到93.84%[12]。Elli Valla等人提出基于机器学习的帕金森病诊断的阿基米德螺旋绘图测试，对DraWritePD和 PaHaW两个数据集通过提取高阶导数、角度类型和类积分特征来进行疾病诊断，嵌套Wrapper方法精确度分别达到84.33%和73.71%，非嵌套Wrapper方法准确率为92.16%和84.86%，在一定程度上证明了non-nested方法在疾病数据特征选择研究的可能性。

本文提出了一种基于Wrapper的改进教学优化算法[13](Improved Teaching-Learning-Based Optimization Algorithm，ITLBO)特征选择策略，该方法通过自适应教学因子，来增强个体的个性化学习，进而提高算法精密搜索的性能，使用多学习策略增强算法的全局搜索能力，加速算法收敛，并通过KNN和十倍交叉进行分类预测。

1 TLBO的基本原理

Rao等人提出了教学优化算法(Teaching-Learning-Based Optimization Algorithm，TLBO[12]，TLBO算法与遗传算法、粒子群算法、人工蜂群算法等群智能优化算法相比，其特殊之处在于没有过多的参数需要设置，而是只需要设置种群大小、迭代次数等几个共有的基本参数，在实际问题中更具有灵活性。

教学优化算法主要模仿了教师的教学和学生的学习，通过教师的教学和学生的相互学习来提高全班的平均成绩。教与学算法主要分为教学阶段和学习阶段，班级是学生(种群)集合，“教阶段”是向老师(最优解)学习，“学阶段”中学生(种群个体)之间互相学习[14]，算法具体流程如图1所示。

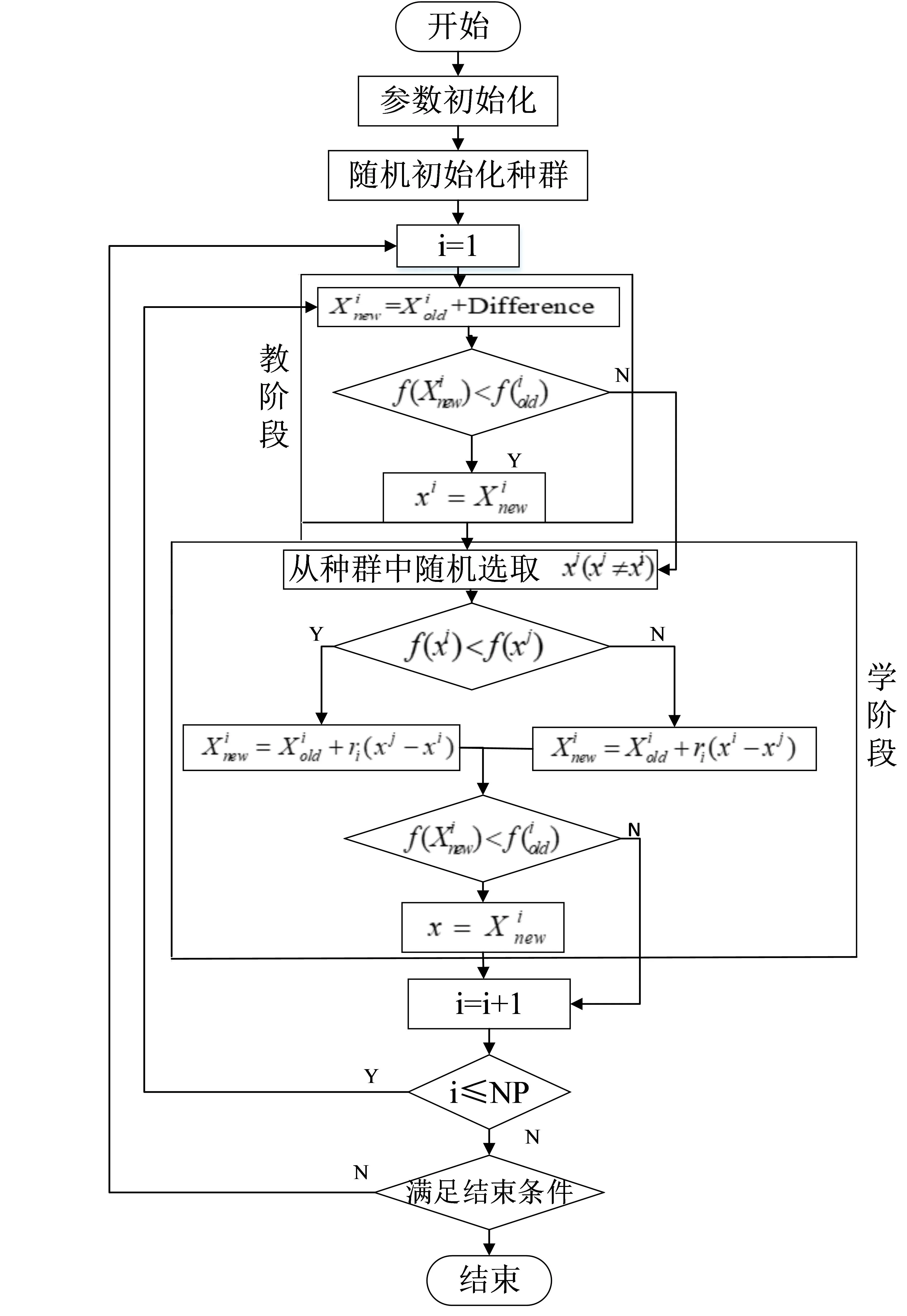
图1 教学优化算法基本流程图

(1)教学阶段

教学阶段，学生向教师学习，即尽可能让全体学生在知识方面达到他的水平。假设在第i次迭代中，有m个决策变量，学生总数为n(k=1,2,...,n)，Mj,i为全体学生在决策变量j(j=1,2,... ...,m)的平均值，在当前迭代次数中目标函数最优的学生记为xbest即老师。因此，当前全体学生在每个变量的平均值于教师的每个变量差值的计算如公式(1)：

(1)

其中，Xj,xbest,i为教师xbest在第i次迭代中的第j个决策变量；ri表示学习步长，取值为0～1之间的随机数；TF为教学因子，随机取值为1或者2。为了尽可能让全体学生在知识方面达到教师的水平，因此需要更新每个学生的决策变量值更新如公式(2)：

(2)

(2)学习阶段

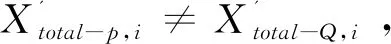
(3)

2 基于改进教学优化算法的特征选择

TLBO算法参数较少、易于理解、方便使用，但存在求解精度不高、局部搜索能力较差等问题，针对此问题，本文提出了一种基于改进的教学优化算法(ITLBO)，该在原有的教学优化算法基础上通过自适应教学因子，提高算法精密搜索的性能，使用多学习策略增强算法的全局搜索能力，加速算法收敛。

2.1 初始化

对原始数据集执行预处理的过程称为初始化，即把数据初始化成为一个用二进制编码的二维数组。每一个解集都是一个二进制字符串，被选中的特征该维数据为1反之为0，之后引导算法进一步搜索更新。

2.2 目标函数设置

在智能算法的寻优过程中会始终有特征子集评估的环节。在某些情况下，在增加准确率的同时也能减少所选特征数目。特征选择被视为组合优化问题，为了获得最优解，首先要选择一个合适的目标函数当作算法迭代过程的评判标准，适应度函数原则上应该能够平衡最大分类精度和最优特征子集两个主要目标。本文适应度函数具体计算方法如公式(4)和公式(5)所示[15]：

(4)

(5)

其中，P表示分类器模型经过十倍交叉验证所得到的精确度，其计算公式如(5)所示，其中，numc是分类正确的数目，numi是分类错误的数目。另外，十倍交叉验证是为了降低由训练集和测试集单次划分所导致的偶然性，更加充分利用现有数据集，对其进行多次划分，进而能够避免因特殊划分而选择泛化能力不好的偶然参数和模型。n是被选中的特征数目，N是总特征数目，α和β分别表示分类器的精度、所选特征数目的权重，其中α+β=1。

2.3 自适应教学因子

在基本的教学优化算法的教学阶段，教学因子的取值只有0和1两种情况，这样就造成了学生学习方式过于单一，对于老师的教的知识也只能有全部接受和全不接受两种情况，不利于个性化教学，这样就不符合现实生活中班级教学的模式。为了加强个性化教学，进而提高种群个体多样性，采用改进源于粒子群算法[16]中线性递减惯性权重进行改进，具体计算如公式(6)所示：

(6)

其中，TFmax为TF的最大值，TFmin为TF的最小值，MaxIter和iter分别代表最大迭代次数和当前迭代次数。

2.4 多学习策略

多学习策略中，学生可以通过不同的方式提高自己的知识水平：1)学生之间的随机交流：学生可以自发地选择成绩较好的学生进行学习，提高知识储备；2)通过教师反馈学习：教师根据学生的学习情况给予相应的反馈[17]，在这个过程中，学生可能会有误解他们自身所学到的知识，即陷入局部最优，因此需要经常求教老师，学习效率才会提高，进而提高算法精度。这一阶段更新策略如公式(7)所示：

Xnew,i=

(7)

其中，rand取0到1之间的随机数，TFi为当前教学因子的取值。

ITLBO特征选择算法伪代码如表1所示：

表1 ITLBO伪代码

3 实验结果与分析

3.1 实验配置

本次实验基于Spyder开发环境中python3.8中实现，实验初始种群数量为40，最大迭代次数为80，每个实验重复十次，取平均值作为最终结果。

3.2 数据集描述

本文采用的是UCI(http://archive.ics.uci.edu/ml/datasets.php)机器学习库公开的帕金森疾病数据集,该数据集一共收纳了31个人的声音数据，其中帕金森疾病患者有21名。数据集一共有193条，23个属性列。其中，“status”列取值为0代表不是该疾病患者，取值为1代表该疾病患者，具体描述如表2所示。

表2 数据集属性描述

3.3 评价指标

该数据集属于二分类问题，本文采用根据混淆矩阵(如表3所示)所得出的准确度(Accuracy)、特异度(Specificity)、召回率(Recall)、精确度(Precision)、F1-Score和适应度函数值对所选特征子集进行评估。

表3 混淆矩阵

其中，TP为真正类样本数；FP为假正类样本数；FN为假负类样本数；TN为真负类样本数。各个评价指标的计算公式如下。

(1)准确度(Accuracy)是用于评估分类模型的指标，是指模型预测正确的结果所占比例(包含正例和负例)，具体计算如下所示：

(8)

(2)特异度(Specificity)是预测出来的负类占实际上负类的比例，具体计算如下所示：

(9)

(3)召回率(Recall)是指正类样本中，被正确识别为正类别的个体所占比例，具体计算如下所示：

(10)

(4)精确度(Precision)是在预测为正类的样本中，实际上属于正类的样本所占的比例，具体计算如下所示：

(11)

(5)F1-Score是将精确度与召回率结合计算的实际评分准则，是精确度与召回率的调和平均，具体计算如下所示：

(12)

其中，P代表精确度，R代表召回率。

3.4 结果分析

不同的分类器模型对算法的精度有一定的影响，本实验首先验证了K近邻(KNN)、朴素贝叶斯(NB)、支持向量机(SVM)和决策树(DT)四种分类器模型在帕金森疾病数据特征选择性能的影响。实验发现KNN分类器模型表现最好，具体实验结果如表4所示。在后续实验过程中，通过调参选取了KNN分类器中K的取值，这样能够保证每次的分类精度尽可能高。

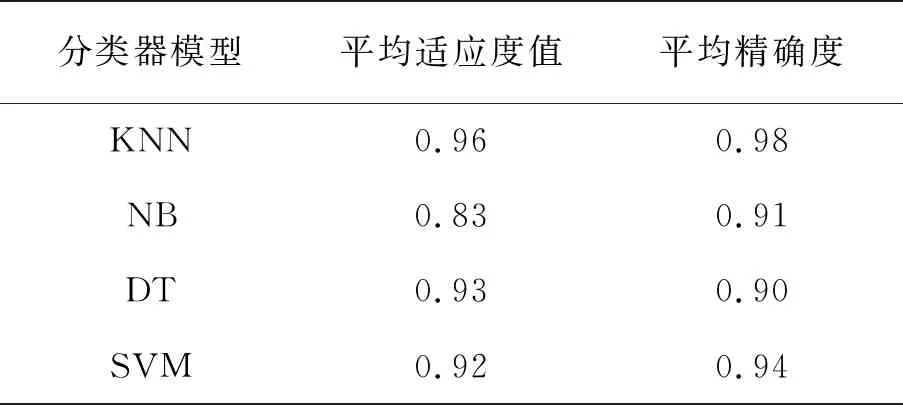
表4 不同分类器结果对比

由表4可知，KNN分类器模型的平均适应度为0.96，平均精确度为0.98，高于NB、DT和SVM分类器，因此本次实验以KNN作为分类器进行分类验证。实验表明，改进之后，算法的收敛速度加快，准确率也有所提升，具体在帕金森疾病数据集上的评价指标如表5。如图4所示，算法在执行20次时就趋于收敛，且适应度值达到0.958。实验所记录的所选特征中被选中超过5次的特征分别为：第一列(MDVP:F0(Hz))，第十五列(NHR)，第十六列(HNR)，第十七列(RPDE)，第十八列(DFA)，第十九列(Spread1)，第二十二列(PPE)，被选中的次数明显高于其他特征。与参考文献[18]中所选特征有五列是相同的，但是相比精度而言，ITLBO精度高了2.4%。

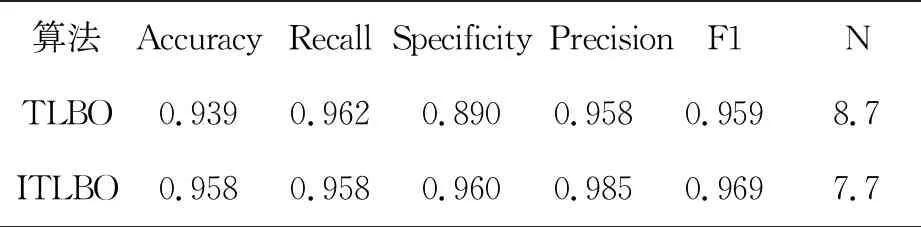
表5 评价指标对比

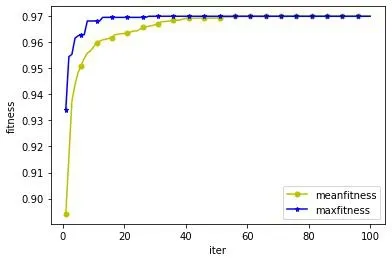
图2 适应度曲线

3.5 算法性能评估

为进一步验证ITBLO算法的性能，本环节在UCI公开数据集中选取另外三种数据：肝炎(实体：150个，属性：20列)、心脏病(实体：303个，属性：14列)、Ionosphere(实体：351个，属性：35列)进行对比分析验证。实验结果如表6所示。

由表6可知，在PD数据上，ITBLO算法的Accuracy提高了0.02，Specificity提高了0.06，精度提高了0.03，F1-Score和适应度值均提高了0.01。在肝炎和心脏病数据集中，准确率、召回率、精确度和F1数值都有较大提高；在Ionosphere数据集中，虽然Accuracy和Recall低于TLBO，分别为0.85和0.65，但是特征总数低于TLBO的0.94，为0.76。通过不同数据集的多次实验对比分析，ITLBO性能相比于TLBO在各项评价指标上均有所提高，同时在一定程度上验证了算法的改进策略的可行性。

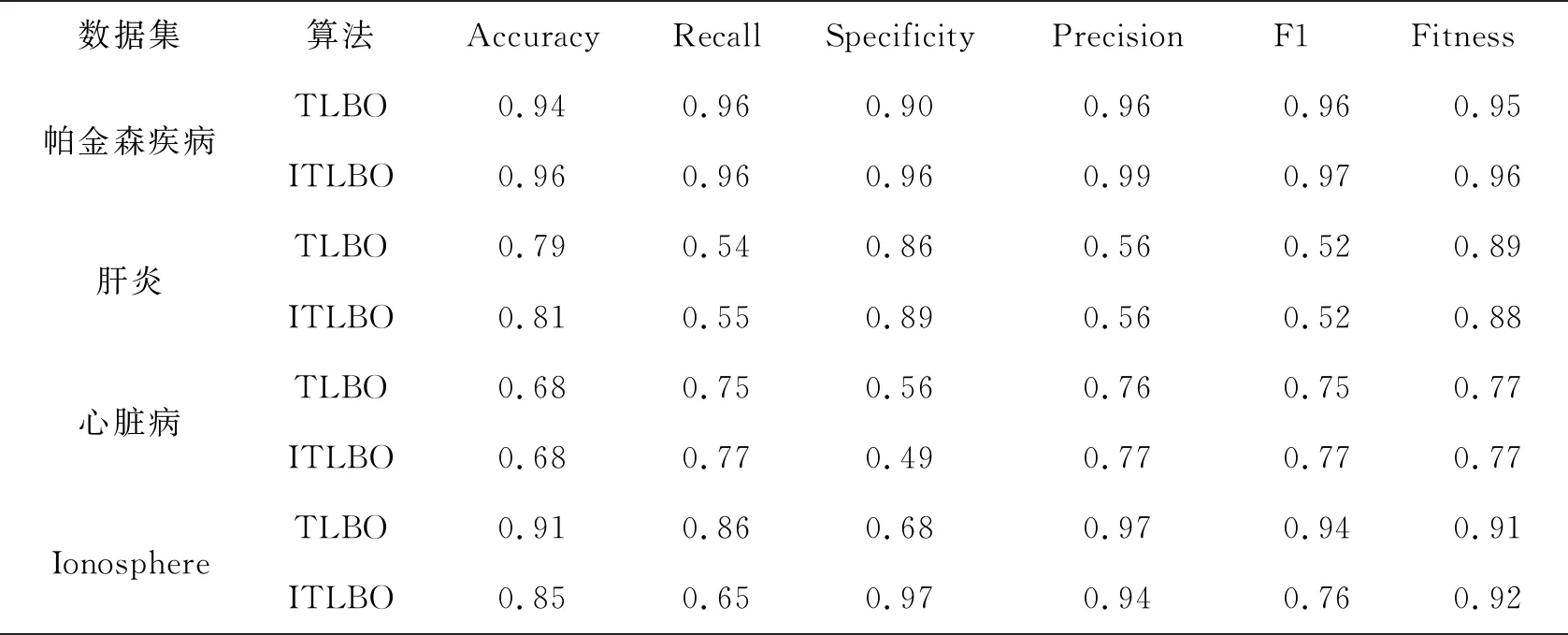
表6 在不同数据集上的性能对比

4 结束语

帕金森疾病作为第二大神经系统疾病，主要表现为静止性震颤、运动迟缓、肌强直和姿势步态障碍，同时患者可伴有抑郁、便秘和睡眠障碍等非运动症状，目前暂无有效治疗方案。本文基于TLBO算法提出了基于二进制特征选择应用的ITLBO算法，应用在UCI公开的Speech PD数据集上，并通过K近邻(KNN)、朴素贝叶斯(NB)、支持向量机(SVM)和决策树(DT)四种分类器进行性能评估，实验结果表明，相较于原始的TLBO算法，ITLBO-KNN算法性能更优。这为进一步研究帕金森疾病提供了一定的参考，对为特征选择方法的研究提供了一种新策略。