广义平衡定制邻近点算法
2022-03-06陈智琦
申 远,陈智琦
(南京财经大学 应用数学学院,江苏 南京 210023)
本文考虑带有线性约束的凸优化问题,形式如下:
min{θ(x)|Ax=b,x∈χ},
(1)
这里χ⊆Rn是有界闭凸集,θ:χ→R是一个凸函数(但不一定光滑),以及A∈Rm×n,b∈Rm。问题(1)的解集记为χ*,并且假设其非空。
为了求解问题(1),目前已经有许多有效的算法,例如Powell[1]和Hestenes[2]提出的增广拉格朗日乘子法(augmented Lagrangian method,简称ALM)是一种经典的算法,其迭代格式如下:
(2)
β>0为惩罚参数。
由Moreau[3]提出的邻近点算法(proximal point algorithm,简称PPA),该算法由Kaplan和Tichatschke[4],Martinet[5]等人推广。何炳生[6]提出了带线性邻近项的邻近点算法(Proximal-Point Algorithm Using a Linear Proximal Term,简称LPPA),何炳生和袁晓明在[7]中将Chambolle[8]提出的原始对偶方法解释为经典PPA的应用。在此基础上,何炳生和袁晓明在[9]中提出了定制邻近点算法(customized proximal point algorithm,简称CPPA)来求解问题(1),其迭代格式如下:
(3)
松弛步骤为:
这里的γ为松弛因子,λ∈Rm是拉格朗日乘子,r,t>0是迭代参数。令ω:=(x,λ),Ω:=χ×Rm。由(2)的一阶最优性条件和ωk+1∈Ω,可以得到:
θ(x)-θ(xk+1)+(ω-ωk+1)T[F(ωk+1)+Q(ωk+1-ωk)]≥0,ω∈Ω
(4)
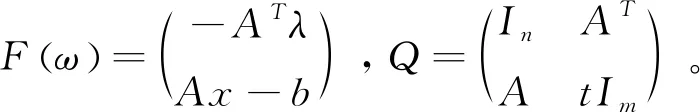
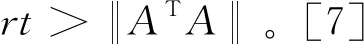
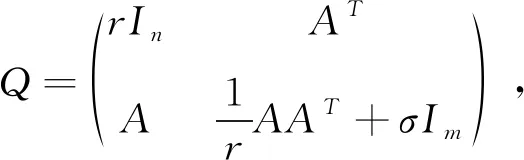
(5)
本文将在第一章提出新的一种平衡定制邻近点算法,第二章给出证明新算法收敛性所需要的一些引理,在第三章证明了新算法的全局收敛性,然后进行数值实验,最后给出全文的总结。
1 广义平衡定制邻近点算法
先介绍一些预备知识,然后给出本文提出新算法迭代以及框架。
问题(1)的拉格朗日函数为
L(x,λ)=θ(x)-λT(Ax-b),
(6)
问题(1)的一阶最优性条件如下:
(7)
定义1以上变分不等式可简记为:
VI(θ,F,Ω)θ(x)-θ(x*)+(ω-ω*)TF(ω*)≥0,∀ω∈Ω,
(8)

本文提出的平衡定制邻近点算法的迭代格式如下所示:
算法1广义平衡定制邻近点算法,GB-CPPA
给定ω∈Ω,由GB-CPPA所生成的新迭代ωk+1∈Ω通过如下步骤所得:
(9)

注记:
与GCPPA算法的参数条件进行对比,当γ=0时, BG-CPPA算法就是GCPPA算法。曲线越靠近坐标轴,参数范围越大(条件越放松),图一表明BG-CPPA曲线在GCPPA曲线的下方,更靠近坐标轴,显然参数条件更加放松。


图1 参数:

图2 参数:
由GB-CPPA的迭代(9)的一阶最优性条件可得:
因此对于∀ω∈Ω,有如下的变分不等式:
将上式写成紧凑的形式,如下所示:
(10)

2 新算法的引理和性质
在证明GB-CPPA算法全局收敛性之前,本文先证明如下的几个引理,这几个引理将在本文所提出的新算法全局收敛性证明中起到重要作用。
引理1由定义1中(8)式所定义的解ω*∈Ω*,序列{ωk}是由GB-CPPA算法所生成的序列,因此成立下述不等式:
(11)
证明将x=x*,ω=ω*带入(10)式中,可以得到:
(12)
因为F(ω)的仿射是斜对称矩阵,所以映射F(ω)是单调的,因此
(ωk+1-ω*)TF(ωk+1)≥(ωk+1-ω*)TF(ω*),
(13)
这里ω*∈Ω*是(8)式的一个解,因此
θ(xk+1)-θ(x*)+(ωk+1-ω*)TF(ω*)≥0,
(14)
(13)式与(14)式相加,可得
θ(xk+1)-θ(x*)+(ωk+1-ω*)TF(ωk+1)≥0。
(15)
将(15)式代入(12)式中,可以得到(11)式。引理证明完毕。
下面证明Q是正定矩阵
由上式可知,矩阵Q与矩阵A合同,要证明Q是正定矩阵等价于证明矩阵A是正定矩阵。
令
M=rIn-α2AT(tIm+γATA)-1A。
(16)

引理2由GB-CPPA算法所生成的序列{ωk}满足如下的不等式:
(17)
证明对于任意向量a,b,c,d∈Rn,成立下述恒等式:
令a=ω*,b=c=ωk+1,d=ωk带入恒等式如下:
(18)
令a=λ*,b=c=λk+1,d=λk带入恒等式如下:
(19)
将(18)式、(19)式带入(11)式,整理如下:
(20)
根据式(10)所定义的矩阵Q,可以得到:
(21)
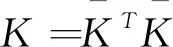
带入(9)式中λ子问题的迭代,并且令K=tIm+γAAT,有如下公式:
(22)
将(22)式代入(21)式,可得:
(23)
把(23)带入(20)式,即可得到(17)式。证明完毕。
3 GB-CPPA算法的收敛性
基于引理2,下面证明由GB-CPPA算法所生成的序列{ωk}的收敛性。
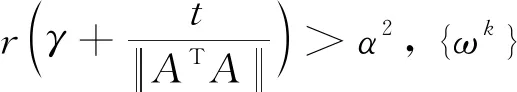
(24)
序列{ωk}收敛于(8)式的解集Ω*中的一个解。
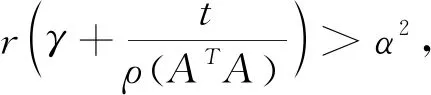
(25)
将(17)式从k=0到k=K(K>1)求和,可得:
(26)
一方面,对于任意的K>1,合并(25)式和(26)式可知:
(27)
由于问题(1)的目标函数是凸函数,它的解集Ω*是一个有界的非空闭凸集。
另一方面,对(26)式的左右两端同时取极限,可得:
(28)

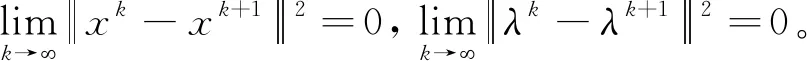
(29)

θ(x)-θ(x∞)+(ω-ω∞)TF(ω∞)≥0,∀ω∈Ω。
因此ω∞∈Ω*是满足(8)式的一个解。证明完毕。
4 数值实验
我们将GB-CPPA算法与GCPPA算法通过数值实验进行比较,来研究新算法的实际计算效率,实验测试在一台配置为Intel(R) Core(TM) i7-7500U CPU 2.70GHz,8GB内存,Windows10家庭中文版操作系统,编程软件为MatlabR2019b。
求解相关性矩阵校正问题,其形式如下:
(30)
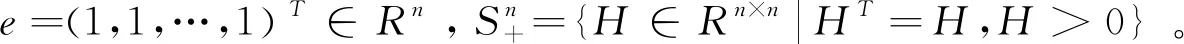
对给定的(Xk,zk),由GB-CPPA算法产生新的迭代(Xk+1,zk+1)格式如下:
(31)
上式中x子问题等价形式如下:
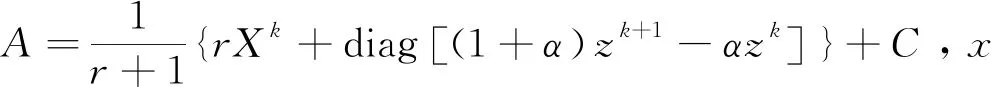
对矩阵A做SVD分解:A=VΛVT, Λ=diag(λ1,λ2,…,λn),V是正交矩阵。
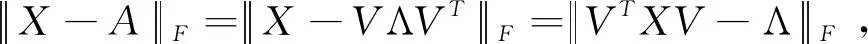

表1 GCPPA与GB-CPPA数值实验结果
在迭代次数和运行时间两方面,GB-CPPA算法的数值实验效果均优于GCPPA算法, GB-CPPA算法无论迭代次数还是计算时间均比GCPPA算法快5%~25%不等,平均大约快15%,具体实验结果如图3和图4所示。从图3和图4的变化曲线可知,随着矩阵维数的增长,GB-CPPA算法依然保持着稳定的性能优势。

图3 算法的迭代次数
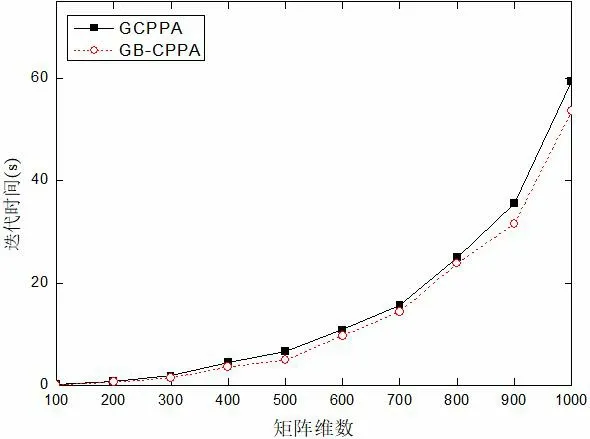
图4 算法的迭代时间
5 总结
在本文中,我们研究了具有线性等式约束的凸优化问题,由于传统的CPPA算法中的参数条件要求较严,基于GCPPA算法和BALM算法,进一步放松了参数条件,提出了广义平衡邻近点算法。本文提出的新的算法,在各种应用程序中更容易实现,在实际问题的应用中更加广泛,并且还证明了新算法的全局收敛性。
