函数变换对灰色建模精度的影响研究
2022-03-06陈心愿陈友军
陈心愿,陈友军
(西华师范大学 数学与信息学院,四川 南充637002)
1982年邓聚龙教授提出了灰色系统理论,灰预测模型作为其中的一个重要组成部分,只需要少量的信息即可完成对未知趋势的预测[1],为系统科学理论提供了新的理论方法,现已被广泛的运用于交通、农业、能源、医疗等领域[2]。为了使灰色模型更加完善,广大学者在数据和模型两方面对原始GM(1,1)模型进行了改进。数据方面:若数据序列受到外部冲击扰动,则先利用缓冲算子消除扰动,再建立GM(1,1)模型;若数据序列未受到外部冲击扰动,则利用函数变换将不适合直接建模的原始序列转变成更适合建模的新序列,利用新序列建模后再还原。模型方面的改进主要有以下几个方面:①灰导数的改进[3-6];②背景值的改进[7-10];③发展系数a和灰作用量b的改进[11-13];④模型的基本形式与模型的白化微分方程结构不一致的改进[14,15];⑤初始值的改进[16-18]等。
本文主要探究数据改进方面:函数变换对灰色建模精度的影响。序列的光滑性、序列的级比偏差以及序列的凹凸性是影响函数变换提高建模精度的主要因素。为提高建模精度,学者们从提高序列光滑度、缩小序列级比偏差、保凹凸性不变等方面出发,提出了一系列的函数变换,并将其运用于各个领域。如肖敬宇、李成龙、杲玄玄等人[19-21]对不满足平滑条件的序列进行对数变换,改进了原始序列的光滑度,提高了灰预测模型的建模效果;刘秋华、黄全华、胡振和戴文战等人[22-25]用幂函数变换改进灰色预测模型,并将其分别运用于电力需求、油气田产量以及人均住房面积等的预测中;叶璟等人[26]运用余切函数变换对不同情形的区间灰数序列进行处理,将灰色数据变换技术的应用范围拓展到了区间灰数预测领域;张军等人[27]研究了反余切函数变换影响建模精度的光滑度、级比偏差和还原误差三方面的性质,得到了新的灰预测模型;宋泉良等人[28]提出了一种能提高序列光滑度,缩小序列级比偏差,保持序列单调性和上凹性的反余割函数变换,并将其与NGM(1,1)模型相结合,得到了具有较高拟合和预测精度的新模型;陈华喜[29]利用正弦函数变换解决了小麦产量呈周期性变化的问题,进一步提高了预测的精度。秦小丽、秦谢勋、赵彦刚等人[30-32]将基于指数函数变换的灰预测模型分别运用于财务风险预警、管道腐蚀预测以及变形监测中,相比传统的灰色模型提高了建模精度;王建根、李春生[33]理论上证明了对数—幂函数变换比单一的对数变换和幂函数变换更能提高序列光滑度;杨跃东和米国芳等人[34,35]将对数—幂函数变换运用于具体的实际问题中,进一步说明了函数变换在灰预测中的重要性。上述这些变换均在一定程度上提高了序列的光滑度或缩小了序列的级比偏差等,从而达到了提高建模精度的目的,但是序列的光滑度、级比偏差、凹凸性等,仅仅是影响序列建模精度的某一方面因素而已,所以基于提高序列光滑度、缩小序列的级比偏差、保凹凸性等这些条件提出的函数变换,并不能保证一定提高所有序列的建模精度。此外,组合变换也不一定能提高序列的建模精度。
1 现有研究基础
1.1 原始GM(1,1)模型建模步骤
设X=(x(1),x(2),...,x(n))为非负原始数据序列。

Step2:计算出一次累加生成序列的均值生成序列Z(1)=(z(1)(2),z(1)(3),...,z(1)(n)),其中z(1)(k)=0.5(x(1)(k-1)+x(1)(k)),k=2,3,...,n。
Step3:利用一次累加生成序列建立GM(1,1)模型,它对应的白化微分方程为
灰色微分方程为
x(k)+az(1)(k)=b
Step4:利用最小二乘法求解参数a,b的值,令
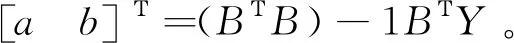
Step5:利用白化微分方程的解近似代替灰微分方程的解,当x(1)(1)=x(1)时,得到GM(1,1)的时间响应序列为
Step6:将上式进行累减还原得到X的时间响应式为
1.2 序列的光滑性[36-39]
定义1设序列X=(x(1),x(2),...,x(n))为非负数据序列,∀ε>0,∃k0,当k>k0,如果光滑比ρ(k)<ε,则称X为光滑离散序列。
定理1X是光滑序列的充要条件是ρ(k)是关于k的递减函数。
定义2对于单调递增非负序列X,经过非负变换f(x(k))之后,如果满足
则称变换后的序列F=(f(x(1)),f(x(2)),...,f(x(n)))比原始序列X更光滑。
定理2若序列X非负,那么非负变换f(x(k))=x(k)g(k)满足
的充要条件是g(k)非负,且严格单调下降。
序列的光滑度是影响原始GM(1,1)建模的重要因素,因此学者基于提高序列的光滑度提出了一系列的函数变换,如常见的对数变换,幂函数变换,对数—幂函数变换,三角函数变换等。
1.3 序列的级比偏差
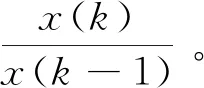
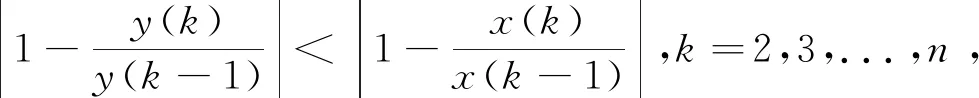
定义5[37](新级比偏差的比较原则)设有非负序列X=(x(1),x(2),...,x(n)),Y=(y(1),y(2),...,y(n)),若有
我们称序列Y比序列X级比偏差更小。
由文献[37]知,对于两个同时单调递增或同时单调递减的序列来说,定义4和定义5的结果是一致的,但是当两个序列一个单增,一个单减时,定义5比定义4更加合理。因此,后面的研究均采用定义5的级比偏差比较原则。
定理3[38]设X为非负序列,若非负变换f(x(k))可表示为f(x(k))=x(k)g(k),其中g(k)非负且严格单调递减,则变换后的序列级比小于原始序列的级比。
为了快速地判断一个非负函数变换f(x(k))=x(k)g(k)是否能缩小序列的级比偏差,本文根据新级比偏差比较原则给出了函数变换f(x(k))=x(k)g(k)缩小级比偏差的条件。
定理4设X为非负单调递增的序列,若非负函数变换f(x(k))可表示为f(x(k))=x(k)g(k),其中g(k)非负且严格单调递减,则
(1)当变换f(x(k))单调递增时,变换后的序列相比原始序列缩小级比偏差。
(2)当变换f(x(k))单调递减时,只要满足条件
则变换后的序列相比原始序列缩小级比偏差。
证明(1)当变换f(x(k))单调递增时,f(x(k))的级比偏差为
x(k)的级比偏差为
因为x(k),f(x(k))单调递增,所以
又因为g(k)单调递减,所以
因此
所以
所以变换后的序列缩小级比偏差。
(2)因为x(k)单增,f(x(k))单调递减,所以
又因为
则
因此
所以变换后的序列缩小级比偏差,得证。
级比偏差越小,数据就越平缓,序列就越适合建模,可见序列的级比偏差是影响建模精度的一个重要因素;所以广大研究者基于缩小序列级比偏差这一条件,提出了一系列的函数变换,如常见的对数变换,幂函数变换,对数—幂函数变换。
1.4 序列的凹凸性[36-37]
定义5设序列X=(x(1),x(2),...,x(n)),若对任意的k=2,3,...,n,都有
则序列X是上凹的,若不等号反向,则序列是上凸的。

2 探究函数变换对建模精度的影响
提高序列光滑度、缩小序列级比偏差以及保序列凹凸性不变只是函数变换能提高建模精度的主要因素,并不是唯一因素,因此,针对某特征序列能提高建模精度的函数变换并不一定适用于其他序列。但是文献[40]却表示存在一定能提高建模精度的函数变换,下面将用具体实例说明它的结论是错误的;同时指出了文献[37]中多种变换组合后一定能提高建模精度也是错误的,并给出了一种解决还原相对误差扩大的方法。
2.1 实例验证单一函数变换不一定能提高建模精度
文献[40]基于缩小序列的级比偏差、提高序列光滑度提出了一种能提高建模精度的函数变换,给出了一定能提高建模精度的参数范围,并给出了具体的定理论证。下面针对序列为单调递增的情况用具体实例说明文献[40]的结论是不正确的,对于单调递减的情况,有兴趣的读者可以自行验证。
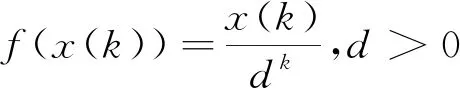
实例1[41]:以某轴承套随时间的磨损为例进行预测,该轴承套已经过磨合期,且每半月对其做一次磨损测量记录,得到磨损量数据如表格1所示

表1 轴承套的磨损记录
按文献[40]的方法建模,计算得到了原始序列的级比平方序列为
(1.0308, 1.0304, 1.0400, 1.0392, 1.0482, 1.0471, 1.0646)
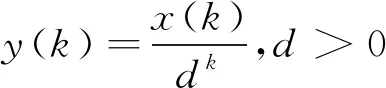
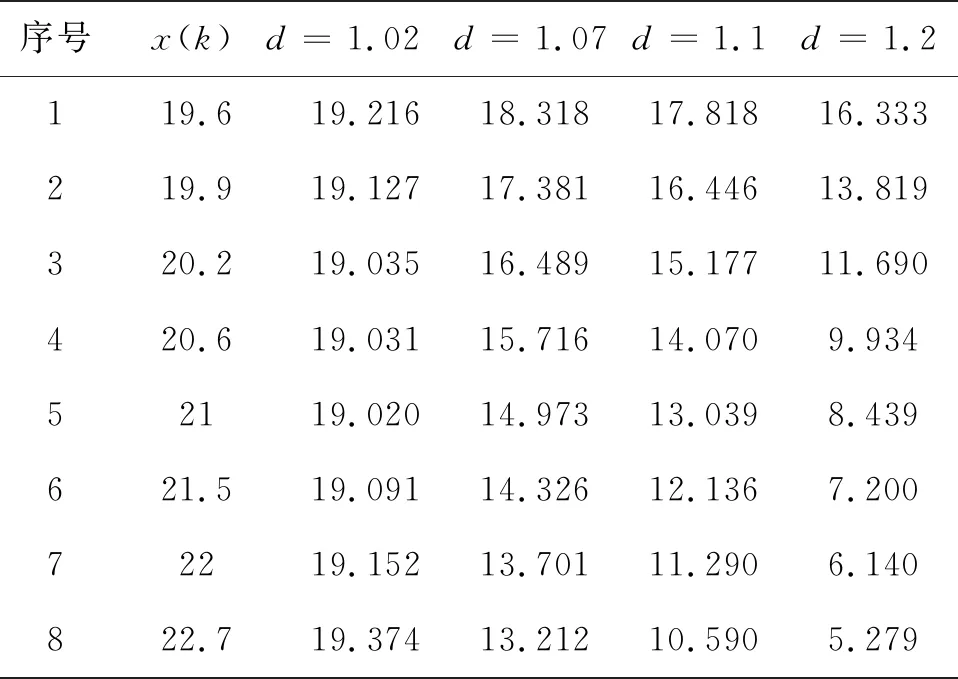
表2 不同的d所对应序列Y

表3 不同的d所对应序列的级比偏差对比

表4 建模效果对比
2.2 组合变换不一定能提高建模精度
文献[37]的最后指出对于还原误差扩大的变换,如常见的对数变换、幂函数变换、对数—幂函数变换等,只需再做对称变换和平移变换就能保证模型精度提高,也即组合变换一定能提高建模精度。但是2.1的研究已经说明了,提高序列光滑度、缩小序列级比偏差等只是影响函数变换提高建模精度的部分影响因素,并不是唯一的。当然,凹凸性也只是其中的一个因素,所以,即使这些变换组合起来也只是进一步加大了函数变换提高建模精度的可能性,并不一定能提高序列的建模精度。但是针对某一个具体的数据序列,我们想要找到能提高建模精度的组合变换还是可能的。
文献[37]指出对称变换可以改变序列的凹凸性,平移变换可以改变序列的正负性,能在一定程度上消除函数变换还原相对误差扩大的影响,进一步提高建模精度。但是需要注意的是上述两个变换只是从凹凸性这一方面进一步改进了建模序列,使其更适合建立模型,实际上并没有解决还原相对误差扩大的问题。下面将给出一个解决函数变换还原相对误差扩大的方法。
定理7设序列为X=(x(1),x(2),...,x(n)),函数变换为y=f(x(k)),那么该变换还原不扩大相对误差的充要条件是
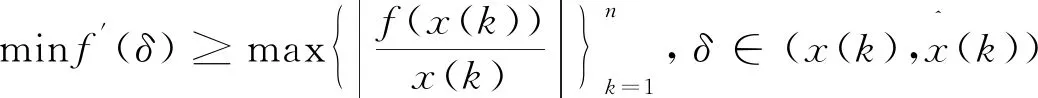
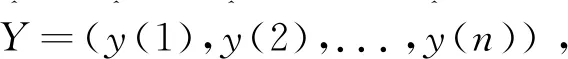
综上,不仅可以通过函数变换改变序列的凹凸性,进一步加大提高建模精度的可能性,还可以根据定理7解决函数变换还原相对误差扩大的问题,在最大程度上提高序列的建模精度。如变换f(x(k))=x(k)∂,当|∂|≥1时变换还原不扩大相对误差,以及对数变换f(x(k))=ln(x(k)),当0 根据上述研究,本文给出了一个函数变换能较大程度上提高建模精度的建模步骤: (2)根据原始序列选择具体的函数变换,当原始序列非负且增长过快时,可以选择对数变换、幂函数变换、对数—幂函数变换,如果光滑度是影响该序列建模精度的主要因素,可以选择更能提高序列光滑度的对数—幂函数变换;当序列是振荡序列时,可以选择三角函数变换或者指数函数变换,都能得到比较好的效果。最后,要求变换后的新序列更加光滑,级比偏差更小。 (4)根据函数变换计算出相应的y(k),判断序列Y是否呈上凹趋势,如果不是,可以通过对称变换和平移变换将其转变成呈上凹趋势的序列,然后建立GM(1,1)模型进行预测;如果已经是呈上凹变化的序列,则直接建立GM(1,1)模型进行预测。 因为函数变换的形式非常多,所以这里只给出了几种常用函数变换:对数变换、幂函数变换、对数—幂函数变换、三角函数变换、指数函数变换的选择建议。针对负数序列,利用平移变换转变成非负序列即可。 从函数变换提高建模精度的以往研究出发,实例验证了提高序列光滑度、缩小级比偏差、保凹凸性等只是影响函数变换提高建模精度的部分条件,而不是唯一条件。因此,现有的函数变换不具备普遍适用性,不一定能提高序列的建模精度;组合变换也不一定能提高序列的建模精度。综上,通过将序列经函数变换后建模再还原的方法提高建模精度的内部机理还有待进一步研究。最后,本文给出了一种解决函数变换还原相对误差扩大的方法,以及能较大程度上提高建模精度的函数变换建模步骤。3 函数变换建模的新步骤
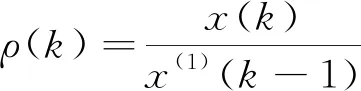
4 总结
