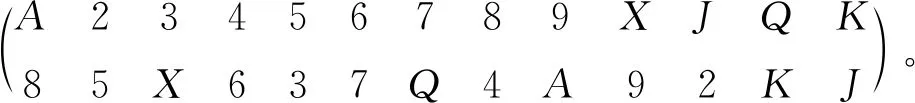置换群及其在对称变换和现实生活中的应用
2022-03-06卢梦霞
卢梦霞,林 昊
(1.周口师范学院 数学与统计学院,河南 周口 466001;2.确山博世学校,河南 驻马店 463200)
群论的研究最早就是从研究置换群开始的,伽罗瓦利用置换群解决了代数方程是否可用根式求解的问题;艺术家和科学家利用置换进行艺术创作和科学研究,设计和构造美妙的图案;物理学家利用置换来研究晶体;化学家利用置换研究晶体内部的结构。置换群在各个领域的应用越来越广泛,本文主要研究置换群的基本性质和在一些方面的应用。
1 预备知识
定义1[1]n次对称群Sn的任意一个子群,都叫做一个n元置换群(简称置换群)。即由有限个置换对于变换的乘法所构成的群。
定义2[1]设集合A={1,3,…,n}(n>1),一个置换σ如果把数码i1变成i2,i2变成i3,…,ik-1变成ik,又把ik变成i1,但别的数码(如果还有的话)都不变,则称σ是一个k-循环置换,简称循环置换,表示为
σ=(i1i2…ik)=(i2i3…iki1)=…=(iki1…ik-1)。
2-循环置换简称对换,无公共数码的循环置换称为不相连循环置换。
定义3[2]几何中的反射、旋转、反演和平移交换统称为对称变换。使图形不变形地变到与自身重合的变换称为图形的对称变换。
定义4[2]经过对称变换保持不变的图形,即完成这种变换前后的图形重合,称此图形为对称图形。
定义5[2]设有某一几何图形,由此图形的全部对称变换对变换的乘法所构成的群称为该图形的完全对称群(也称为该图形的对称变换群)。
命题1[2]凡对称图形,总存在若干个非恒等对称变换和恒等变换一起构成该图形的完全对称群。反之,如果一个图形存在着非平凡的对称变换,则该图形就是对称图形。
Δ:不是对称图形,就不能有非恒等的对称变换。
定理1[1]含有n个元素的集合共有n!个双射变换。
Cayley定理2[1]任何群都同一个双射变换群同构。
定理3(J.I.Lagrange)[1]设H是有限群G的一个子群,则|G|=|H|(G:H)。
2 置换群的性质
性质1不相连循环置换相乘时可以交换[3]。
证设M={1,2,…,n},σ、τ为M上两个不相连的循环置换.记
σ=(i1i2…ik),τ=(j1j2…js)。
∀a∈M,
①当a∈σ时,则a∉τ,
στ(a)=σ(τ(a))=σ(a),τσ(a)=τ(σ(a))=σ(a),
因此στ(a)=τσ(a)=σ(a).即στ=τσ。
②当a∈τ时,则a∉σ,
στ(a)=σ(τ(a))=τ(a),τσ(a)=τ(σ(a))=τ(a),
因此στ(a)=τσ(a)=τ(a).即στ=τσ。
③当a∉σ,a∉τ时,则
στ(a)=σ(τ(a))=a,τσ(a)=τ(σ(a))=a,
因此στ(a)=τσ(a)=a.即στ=τσ。
综上所述,不相连循环置换相乘时可以交换.
性质2每个置换都可以表示为循环置换或不相连循环置换的乘积;每个循环置换可以表示成对换之积;因此,每个置换都可以表示为对换之积[1]。
证任何一个置换均可以把构成一个循环置换的所有数码按连贯顺序紧靠在一起,而把不动的数码放在最后.对任意置换σ有
σ=
=(i1i2…ik)…(j1j2…js)。
即置换σ表示成了不相连循环置换的乘积。
(i1i2…ik)=(i1ik)(i1ik-1)…(i1i3)(i1i2);
或
(i1i2…ik)=(i1i2)(i2i3)…(ik-1ik);
亦或
(ika…binc…d)=(ikin)(ika…b)(inc…d),然后进一步分解成对换。
性质3[1]任何n阶有限群都同一个n阶置换群同构。
性质4k-循环置换的阶为k;不相连循环置换乘积的阶为各因子的阶的最小公倍数。
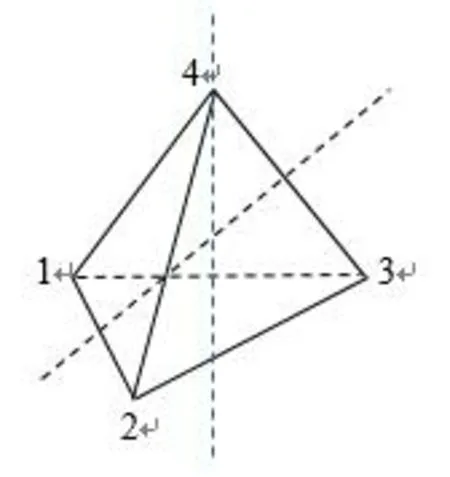
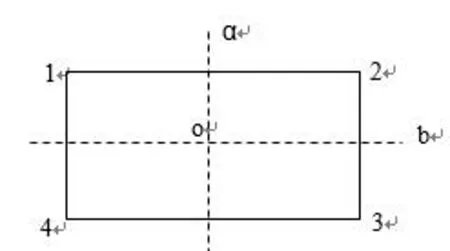
证当1≤m (i1i2…ik)的阶是k.即k-循环置换的阶为k[1]。 设σ=σ1σ2…σs,其中σ1,σ2,…,σs分别是阶为k1,k2,…,ks的不相连循环置换,记k1,k2,…,ks的最小公倍数为t,即t=[k1,k2,…,ks]。则由性质2.1知不相连循环置换相乘时可以交换,又ki|t,故σit=(1),故 (σ1σ2…σs)t= =σ1tσ2t…σst=(1)。 设σ1σ2…σs的阶为r,则r|t,且(σ1σ2…σs)r=(1),则有 (σ1σ2…σs)r= =σ1rσ2r…σsr=(1)。 由于σ1r,σ2r,…,σsr仍是不相连循环置换,而不相连循环置换的乘积不能是(1)。因此只有 σir=(1),i=1,2,…,s。 又因为σi的阶为ki,故ki|r,i=1,2,…,s.从而t|r,故r=t,即σ1σ2…σs的阶为t,t=[k1,k2,…,ks]。 证设k=1,2,…,n, στσ-1(σ(k))=στ(σ-1σ(k))=στ(k)=σ(τ(k))=σ(ik)。 推论 ①当τ=(i1i2…ik)时,则στσ-1=(σ(i1)σ(i2)…σ(in)); ②当τ=(i1i2…ik)(j1j2…js)时,则 στσ-1= (σ(i1)σ(i2)…σ(ik))(σ(j1)σ(j2)…σ(js))。 性质6[4]如果一个n元置换唯一地表示成k个不相连的循环置换的的乘积,那么这个置换可以表示成至少n-k个对换的乘积。 性质7[1]一个n元置换群G中的置换或者全是偶置换,或者奇、偶置换各占一半。 性质8一个k-循环置换(i1i2…ik)左乘以一个对换,可以得到一个置换,该置换可以表示成两个不相连循环置换的乘积,且这两个循环置换的阶的和为k。 证(i1i2…ik)左乘以任意一个对换(isit),设k≥5且is,it都不等于i1、i2和ik。 (isit)(i1i2…is…it…ik)= 其中(i1i2i3…is-1itit+1…ik)的阶为s-1+k-t+1,(isis+1…it-1)的阶为t-s。其和为(s-1+k-t+1)+(t-s)=k。 若is,it等于i1、i2和ik中的某一个时,类似说明;若k≤4时,只需逐个验证即可。 因为S4是有限群,用lagrange定理求子群,根据子群的阶是群的阶的因子,确定子群中的元素个数,根据元素的阶是群的阶的因子,确定子群中的元素,从而求出所有子群。 例1求 S4={(1),(12),(13),(14),(23),(24),(34),(123),(124),(132),(134),(142),(143),(234),(243),(1234),(1243),(1324),(1342),(1423),(1432),(12)(34),(13)(24),(14)(23)} 的所有子群。 解|S4|=24,设H是S4的任一子群,由定理3知 |H||24, 因此|H|=1,2,3,4,6,8,12,24。 (1)当|H|=1时,H1={(1)}。 (2)当|H|=2时,H2={(1),(12)};H3={(1),(13)};H4={(1),(14)}; H5={(1),(23)};H6={(1),(24)};H7={(1),(34)}; H8={(1),(12)(34)};H9={(1),(13)(24)};H10={(1),(14)(23)}。 (3)当|H|=3时,H11={(1),(123),(132)};H12={(1),(124),(142)}; H13={(1),(134),(143)};H14={(1),(234),(243)}。 (4)当|H|=4时, H15={(1),(1234),(13)(24),(1432)};H16={(1),(1243),(14)(23),(1342)}; H17={(1),(1324),(12)(34),(1423)};H18={(1),(12),(34),(12)(34)}; H19={(1),(13),(24),(13)(24)};H20={(1),(14),(23),(14)(23)}; H21={(1),(12)(34),(13)(24),(14)(23)}。 (5)当|H|=6时, H22={(1),(12),(13),(23),(123),(132)};H23={(1),(12),(14),(24),(124),(142)};H24={(1),(13),(14),(34),(134),(143)};H25={(1),(23),(24),(34),(234),(243)}。 (6)当|H|=8时, H26={(1),(13),(24),(12)(34),(13)(24),(14)(23),(1234),(1432)}; H27={(1),(14),(23),(12)(34),(13)(24),(14)(23),(1243),(1342)}; H28={(1),(12),(34),(12)(34),(13)(24),(14)(23),(1324),(1423)}。 (7)当|H|=12时, H29={(1),(123),(132),(134),(143),(124),(142),(234),(243),(12)(34),(13)(24),(14)(23)}。 (8)当|H|=24时,H30=S4。 由群的定义可以看出,代数运算、结合律、左(右)单位元、左(右)逆元,均出现左右对称的本质属性,因而可以用群来研究对称性。 三维空间中正多面体保持空间位置不变的旋转,每一个旋转对应其顶点集合的是一个置换,两个置换相乘就是一个旋转接着另一个旋转,一个旋转的逆就是与它反向的旋转。因此,所有旋转构成一个群,称为此多面体的旋转群(也是一种对称变换群),可用一个置换群来表示。 数域F上任何一个n元多项式f(x1,x2,…,xn),总有集合S={x1,x2,…,xn}上的n次置换使f不变,至少有恒等变换,由于使f不变的任意两个n次置换之积仍使f不变,使f不变的全体n次置换作成一个n次置换群,是Sn的一个子群,称为n元多项式f的n次置换群。 5.1.1 在四面体中的应用 例2正四面体的对称变换群,恒等变换(1),通过四个顶点的三阶轴的变换: (123),(132);(234),(243);(134),(143);(124),(142);连接不相交边中点的二阶轴的变换:(13)(24),(14)(23),(12)(34)。 图1 正四面体的对称变换群 正四面体的对称变换群本质上就是置换群S4的12阶子群H29。 5.1.2 在矩形中的应用 例3矩形的对称变换群,恒等变换(1),绕垂直于矩形并通过O的轴线沿顺时针方向转180°的变换(13)(24),直线a的反射(12)(34),直线b的反射(14)(23)。 矩形的对称变换群就是置换群S4的子群H21。 图2 矩形的对称变换群 5.1.3 在正方形中的应用 例4正方形的对称变换群,恒等变换(1),绕垂直于正方形并通过O的轴线沿顺时针方向转90°的变换(1234),转180°的变换(13)(24),转270°的变换(1432),对直线a的反射(12)(34),直线b的反射(14)(23),直线1-3的反射(24),直线2-4的反射(13)。 正方形的对称变换群就是置换群S4的子群H26。 图3 正方形的对称变换群 例5证明Sn(n≥3,n≠4)的正规子群除去(1)与Sn外只有An。 当N∩An=An时,An⊆Sn,由性质7知N=An或N=Sn。 综上所述,Sn(n≥3,n≠4)的正规子群除去(1)与Sn外只有An。 5.3.1 在穿珠中的应用 例6有n个不同的珠子,要求用线把这些珠子穿成若干个环,而且每个珠子只能被一条线穿过,不同的穿珠顺序是不同的穿法,共有多少种穿珠办法? 解把n个珠子分别用1,2,…,n来表示构成一个集合,记为A,则A={1,2,…,n},则n个不同的珠子按照规定的穿珠办法的总数等于n元有限集的所有置换的个数,因为含有n个元素的集合共有n!个双射变换,即n元有限集共有n!个置换。因此,对于n个不同的珠子,共有n!个穿珠办法。 5.3.2 在乱码排序中的应用 例7给出一列乱序的数码,要把它排成顺序数码,每次只能对其中两个数码进行对换,问最少要对换多少次? 解实质就是置换 由性质2知 (61)(5274893)=(16)(58)(5274)(893)= (16)(58)(57)(52)(74)(89)(93)。 5.3.3 在洗牌中的应用 例8设按顺序排列的13张梅花纸牌(为了方便,把10、11、12、13分别用X、J、Q、K代替) A23456789XJQK, 经三次同样方式的洗牌后的顺序变为 6XAQ9KJ748325, 求第一次洗牌后牌的顺序。 解每洗一次牌,相当于对牌进行一次置换,经三次洗牌后所对应的置换为 σ3= σ3是一个13阶循环置换。 σ12=(σ3)4=(A6K594Q2X87J3)4 =(A9X352JKQ7648)。 σ12σ=σ13=(1),σ12=σ-1, 即 σ-1=(A9X352JKQ7648)。 因此 σ=(8467QKJ253X9A)= 85X637Q4A92KJ。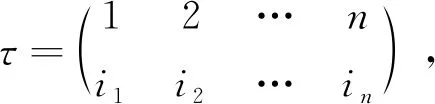

3 置换群S4的子群的求法
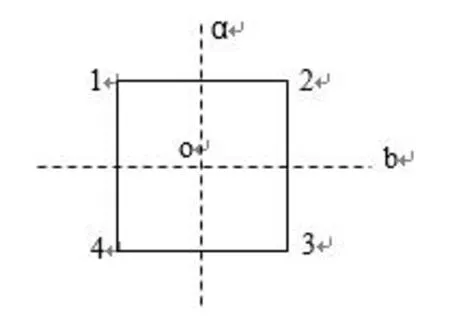
4 置换群与图形的对称变换群问题
4.1 几何对称
4.2 代数对称
5 置换群的应用
5.1 置换群在对称变换群中的应用
5.2 置换在正规子群中的应用

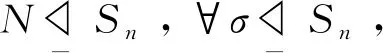
5.3 置换在实际生活中的应用