层结环境下刚性植被群对异重流影响的数值模拟

2022-03-06谢晓云韩东睿林颖典

水利水运工程学报 2022年1期

谢晓云，韩东睿，林颖典

(浙江大学海洋学院，浙江舟山 316000)

异重流是指两种密度差别不大的流体，因密度差导致的重流体入侵轻流体的流动现象[1]。异重流在自然界和实际工程中广泛存在，如水库泥沙冲淤[2-3]、大坝开闸泄洪、河口盐水楔入侵、海底浊流、雪崩等都与异重流有密切联系。植被丛生是典型的外界环境条件，如湿地洪泛浊流遭遇植被、海底浊流途经水下树林等。植被带来的拖拽阻力，可以改变异重流横向和纵向速度分布等运动特性[4-5]。此外，在湖泊、河口、海洋等水体环境中，随着水深的增加，可能产生密度层化水体，如海洋中的温跃层、盐跃层[6-9]等。因此，了解真实环境中异重流运动的演化过程，植被和环境层结是必须考虑的因素。

由于异重流发生的随机性及具备一定程度的破坏性，野外的现场观测并不是首选研究方法。近年来，随着数值方法和计算机技术的快速发展，数值模拟成为了替代手段之一。根据所采用湍流模式的不同，数值模拟主要可分为雷诺平均模拟（Reynolds-Averaged Navier-Stokes Simulation，RANS）、大涡模拟（Large-Eddy Simulation，LES）和直接数值模拟（Direct Numerical Simulation，DNS）[10-12]。相比之下，LES模型的精度比RANS模型的精度要高，可以提供更为准确的流场和浓度信息；在保证足够的精度下，LES模型的计算成本要比DNS模型低。因此，本文将选用LES模型模拟异重流通过植被群的演化过程。

通过对比异重流沿坡运动的二维和三维LES模拟结果，Nourazar等证明了二维模型足以有效准确地捕捉异重流的动力过程[13]。美国爱荷华大学的Constantinescu教授课题组使用LES模型对开闸式异重流和障碍物之间的相互作用展开研究，先后模拟了初始体积分数较大的异重流和多个矩形障碍物之间的作用[14]、不同尺寸的矩形障碍物对异重流运动过程的影响[15]、初始体积分数较小的异重流和多个矩形障碍物之间的作用[16]、异重流和三角形障碍物之间的作用[17]等。最近，Zhou等[18]使用商业软件FLOW-3D研究了障碍物和环境水体水深的相对高度比对异重流运动状态的影响。通过研究泥沙异重流流过矩形障碍物的运动特性，Wilson等[19]发现矩形障碍物的存在会加强异重流的卷吸作用。另一方面，Barcelona等[20]通过研究不同浓度的泥沙异重流流经不同密度植被区域时运动过程，发现异重流的演变与泥沙沉积与植被密度息息相关。贾复等[21]通过开展两层水体中的平坡异重流流态试验得出：在分层水体中容易出现“侵入”型异重流。He等[22]对开闸式异重流在层结水体中沿斜坡运动的水力特性展开研究，完善了在层结水体中异重流沿斜坡运动进入减速阶段的头部速度计算公式，并提出其在加速阶段的头部速度计算公式。进一步地，He等[23]对泥沙异重流于层结水体中沿斜坡的运动特性进行了探索，发现加速阶段异重流受底坡、沉降速度和环境层结度影响很小。Zhou等[18]利用商业软件FLOW-3D搭建的LES模型研究了单个障碍物对开闸式异重流在线性层化环境中沿平坡运动过程，研究结果显示障碍物的高度对异重流的流体特性、运动速度等都有较为明显的影响。进一步地，Zhou等[24]使用LES模型研究了在植被群的影响下，异重流在线性层结环境水体中的运动特性，发现高密度植被会增强异重流的稀释，而高层结度会抑制其稀释，但文中并没有研究异重流运动时能量（势能和动能）的沿程变化及影响。

总体而言，前人综合考虑层结环境和刚性植被群对异重流整体运动特性影响的研究较少，且较少涉及异重流势能及动能的转变。基于此，本文通过使用FLUENT商业软件对层结环境下开闸式异重流通过刚性植被群的运动过程进行数值研究，采用LES模型，利用用户自定义函数（User Defined Function，简称UDF）加入植被阻力效应，考虑植被群高度、环境水体层结等因素，对异重流的形态结构、整体运动特性、瞬时卷吸常数、流体势能、动能等进行分析。

1 数值模型

本研究参照林颖典等开闸式异重流试验[25]，模拟层结环境中异重流流过刚性植被群的运动过程，其物理模型如图1所示。平坡水槽闸门左侧为密度较大的盐水，密度为 ρd，水深h0= 0.15 m，闸室宽x0=0.1 m；右侧为环境水体，利用精密的流量控制系统生成稳定的线性分层水体，其底部水体密度为 ρb，顶层水体密度为ρa，水深H= 0.15 m；与水槽同宽的植被群放置在距离闸门左边界Ld= 0.4 m处，植被简化为直径为d=7 mm的刚性木制圆柱，单位面积内植被所占的百分比为9.0%，其区域长度记为Lv，高度记为Hv。水槽全长为L=2.0 m。试验中，使用高锰酸钾溶液作为示踪剂[25]，以了解异重流的头部位置及形态变化。其中，环境流体的层结度S表示为：

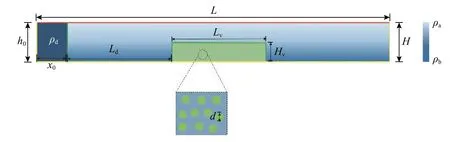
图1 物理模型示意Fig. 1 Schematic diagram of physical model

本文的数值研究对象为如图1所示的开闸式异重流，其计算区域分为初始异重流区域、密度线性分层的环境流体区域和植被区域。在FLUENT中设置不同的层结度和植被高度以研究它们对异重流运动的综合影响。

1.1 控制方程

将计算区域划分为植被区域和非植被区域，并在植被区域定义一个阻力源项，用以模拟植被的阻力[26]。此阻力使用UDF定义，其原理是给动量方程添加一个阻力源项[27]，如式(2)和(3)：

1.2 求解方法

计算区域采用笛卡尔坐标系，使用结构网格进行剖分，采用矩形网格。模型中选用二维的LES模拟，亚格子模型（Subgrid-Scale Model）采用Smagorinsky-Lily假设，多相流模型使用Mixture模型，压力与速度的耦合采用SIMPLE（压力速度耦合方程组的半隐式算法），空间离散中，梯度采用最小二乘法，压力采用PRESTO!算法，动量方程采用有界中心差分格式（Bounded Central Differencing），体积分数采用一阶迎风格式。各计算变量残差小于0.001可认为计算收敛。

顶部边界（图1红色区域）选用剪力为0的边界假设[11]，左、右和下部壁面（图1黄色区域）采用无滑移边界条件。异重流与环境流体分界面及植被区域周围边界（图1绿色区域）采用interior（内部边界）条件。

1.3 模型验证

首先，将数值模拟和林颖典等的试验研究结果[25]进行对比，以验证模型的准确性。这里采用文献[25]中的典型工况S3（植被区域长Lv= 80 cm，高Hv=15 cm，孔隙率nv=91%，层结度S=0.5）对CD计算式中的常数k进行率定。率定结果表明：当k=30时，数值模型的异重流与环境流体分界面、头部位置结果与试验接近。因此，下文所有数值模型取k=30。同时，为了验证网格的无关性，对比了2.0 mm×2.0 mm、1.5 mm×1.5 mm、1.0 mm×1.0 mm、0.5 mm×0.5 mm网格大小的数值结果，发现1.0 mm×1.0 mm网格结果与0.5 mm×0.5 mm网格几乎一致，且比其余两种网格结果更接近试验结果。因此，出于准确性和节省计算资源考虑，选用网格大小为1.0 mm×1.0 mm，共计数量为30万个。

从图2中可以看出异重流头部位置随时间变化的数值结果与试验结果具有很好的一致性。因此，本文使用的二维LES模型并结合UDF加入植被阻力效应，可正确模拟异重流的运动过程。

图2 异重流头部位置随时间变化的数值研究与林颖典等试验结果[25]对比Fig. 2 Comparison of head position of gravity current with time between numerical and experimental results

2 特征参数及工况组别

本研究参数工况分为N系无植被工况、S系工况（浸没式植被工况，即植被高度小于水深）和E系工况（非浸没式植被工况，即植被高度不小于水深）；ρa和 ρd分别为1 000和1 020 kg/m3；其他具体参数如表1所示。

此外，本文工况中对应于控制方程（2）和（3）的相关参数分别为：孔隙率nv=0.91，植被数目N=748株，植被直径d=7 mm，植被区域面A=0.32 m2，单位体积的迎流面积a=16.362 5 m2，植被修正系数k取30，盐水运动黏度v取9.83×10-7m2/s。

表1 数值工况参数设置Tab. 1 Parameters of numerical simulations

3 结果分析

3.1 流态分析

图3为异重流在均匀（左图）和线性层结水体（右图）中的发展过程，且均分别选取了6、12和36 s共3个典型时刻，其中绿色方框指植被区域、黑色箭头指异重流的头部位置。对比图3(a)、(b)和(c)可知：在运动的早期（6 s），异重流的运动情况相同，这是因为异重流的发展还未受到植被区域的影响；随着异重流运动至植被区域，植被阻力弱化了异重流与环境流体交界面的剪切不稳定过程，抑制了Kelvin-Helmholtz（以下简称K-H）涡的形成，尤其是非浸没式工况下（图3(c)），几乎没有K-H涡的形成，且异重流的头部由典型椭圆形变为 “三角形”，这和前人试验研究结果保持一致[15]。而对于层结工况（图3(d)、(e)和(f)），异重流未运动至植被区域时，流态基本一致。继续向前发展时，无植被工况（图3(d)）下，异重流会经历一个速度缓慢衰减的流动过程，在运动的后期由于异重流头部稀释至密度小于底层水体，头部会有一个略微的抬升（中性层入侵）；浸没式工况（图3(e)）下，由于异重流的头部高度大于植被高度，处于下方的异重流受植被阻滞作用缓慢前进且速度变小，导致异重流的整体运动速度（图3(d)）下降。当异重流越过植被区域时，同无植被图3(d)工况一样，由于浮力损失导致头部会略高于层结水体底部，且较图3(d)工况更不明显。非浸没式工况下（图3(f)），异重流所有部位受到植被的阻滞作用，发展受到极大限制，最后停滞于植被间，但由于植被的阻滞作用过于强烈，并没有产生足够使异重流头部抬升的浮力损失。

3.2 整体运动分析

图4为均匀与线形层结水体中异重流头部的瞬时速度变化过程。从图4可知，在运动初期，由于重力塌陷，异重流头部速度经历一个瞬间加速过程，达到最大值后缓慢衰减，这与Dai的试验结果[28]一致；对比N0、S0和E0（非层结环境）3个工况可知，异重流在未遇到植被前速度大致相等，而在异重流的后半段运动中，N0工况异重流头部最终速度（0.038 m/s）会滞后于S0（0.041 3 m/s）和E0（0.041 m/s），这是因为植被的存在抑制了异重流和环境流体的掺混，头部密度的衰减较无植被工况弱，维持异重流运动的动力较强。从图4 (a)中可以看出，虽然非层结工况（N0）下，异重流运动前半段会领先于层结工况（N1、N2、N3），但在后半段反而会落后于该3种工况，这是因为密度分层会抑制异重流与环境流体的掺混，掺混水平较低意味着密度差致使的驱动浮力得以保留，S系工况也和N系工况具有相同流动优势转换现象。而对于E系工况，由于非浸没式植被能产生较强卷吸抑制作用，使得这一速度优势转换点（速度从优势转变为劣势的转变点）延后，此时异重流运动的快慢完全取决于环境水体的层结度，且层结度越大，异重流运动越缓慢。由此可见，植被和层化环境的存在均会影响异重流的运动。整体上，当植被和层结环境同时存在时，植被高度相同情况下，层结度越大异重流的运动速度就越慢；在相同层结度下，由于植被高度增加使得异重流在纵向上所受阻挡增加，使非浸没式植被对异重流的阻碍作用比浸没式植被强烈。但当这两种因素都不存在时，由于与环境流体的强烈卷吸造成的驱动力损失，异重流头部的速度反而会衰减得更快。

图4 异重流头部位置随流动时间的变化关系Fig. 4 Relationship between the front velocity of current and flow time

3.3 卷吸和掺混

本文使用瞬时卷吸常数（Instantaneous Entrainment Coefficient）来衡量异重流与环境流体的掺混程度，异重流的瞬时卷吸常数为[11]：

式中：Mi为i时刻下满足等密度线ρ*≥0.02时异重流的侧向面积[11]，即异重流在平行于流向方向上所占据的二维空间尺寸；xf,i为i时刻的异重流头部速度；Ub,i为0至i时刻的异重流的平均速度即异重流运动的距离与运动时间的比值；ti为计算开始至i时刻的时间。

图5为异重流的瞬时卷吸常数随头部位置的变化关系。对于这3组工况（N系、S系和E系），层结度越大，相同头部位置处卷吸常数瞬时值越小，这说明层结环境会抑制异重流的卷吸作用。此外，卷吸强度与层结度呈负相关，这是因为层结度越大，异重流与环境流体的密度差越小，异重流水平速度越小，与环境流体的剪切不稳定性就越小，从而导致卷吸作用越弱。而对比非层结工况N0、S0和E0可以发现：植被的存在会降低异重流的卷吸作用，这是因为当异重流流经植被区域时，植被会对异重流产生一个拖曳力，降低异重流头部的水平流速，从而减小异重流与上层速度较慢的环境流体在竖直方向上的速度差，最终引起掺混的K-H不稳定性。且对于无植被非层结工况（N0）异重流发展的后期，瞬时卷吸常数有一个剧烈波动，这说明在这个阶段异重流与环境流体掺混不稳定。这是因为：一方面，开闸式异重流往前传播时，由于头部没有及时得到重流体的补充，导致密度不断被稀释；另一方面，由于K-H涡使一部分重流体被抬升，导致与环境流体的接触面积增大，从而使得卷吸作用增强。对于浸没式植被工况（S0），当异重流流出植被区域时，卷吸常数会有所增大，这是因为失去植被的阻碍作用，异重流与环境流体的剪切不稳定性得以充分发展。而非浸没式植被工况由于较强的阻碍作用，使异重流流出植被区域后的速度不足以产生较强的剪切不稳定性，导致卷吸系数并没有明显增大。对于植被工况（S系和E系），当异重流离开植被区域时，不同层结度工况下瞬时卷吸系数之间差值减小，尤其是E系工况，这说明植被对异重流卷吸作用的影响比环境层化的影响较大，也即当植被和层结环境同时存在时，植被的弱化起主导作用。这是因为在本文工况中，层结环境引起的驱动浮力减小并没有植被对异重流的阻力对速度的影响大。即如果异重流和环境水体密度差足够大时，层结度对异重流掺混抑制的影响可能会强于植被。

图5 异重流的瞬时卷吸常数随头部位置变化关系Fig. 5 Variation of entrainment parameter with front position of gravity current

3.4 势能转换

流体势能是异重流的初始动力源。异重流运动时，总势能一部分转化为维持水平前进的动能，此处称为可用势能；一部分转化为异重流与环境流体交界面上不可逆的掺混耗散能，此处称为背景势能。异重流势能的研究可以有效解决两相流体交界面难以准确界定的难题，背景势能是量化掺混强烈程度的有效参数[11]。参照Winters等[29]对流体能量的定义，异重流体系的总势能Ep(t)、背景势能Eb(t)和可用势能Ea(t)可以分别表示为：

式中：〈 ρ(x,z,t)〉为流场平均密度；V为整个流场流体总体积（包含异重流和环境流体）；〈 ρ~(x,z,t)〉是流场在绝热条件（与外界无热交换）下重新排布为势能最小状态（流场完全稳定水平分层）时的密度场。基于此，可用势能Ea(t)可以理解为〈 ρ(x,z,t)〉绝热转变为〈 ρ~(x,z,t)〉释放的能量。

非层结工况（N0、S0、E0）和对应的层结工况（N3、S3、E3）下，异重流总势能Ep、背景势能Eb和可用势能Ea随异重流沿程头部位置变化的关系见图6。从图6可以看出，在异重流速度恒定的初始坍塌阶段[4]，总势能Ep的变化趋势与可用势能Ea变化趋势高度吻合，而背景势能几乎为0，这说明此阶段总势能完全转变为动能，异重流与环境流体几乎不掺混。背景势能Eb随后逐渐增大，也就意味着发生在异重流与环境流体交界面不可逆的掺混逐渐增强，表现为K-H不稳定性主导的涡旋。总势能曲线与可用势能曲线逐渐分离，直到背景势能与可用势能曲线相交。在相交点之前，表征着异重流的总势能主要用来维持自身向前运动，在相交点之后，表征着异重流的主要势能被卷吸掺混过程所消耗。对比图6(a)、(b)和(c)可知，植被的存在和层结环境会使得相交点提前，这是因为植被对异重流产生较大的阻力，使得直接用以驱动异重流前进的可用势能占比下降更快。层结环境虽然会抑制掺混，但也会导致异重流初始动能下降，两部分因素同时存在时，初始动能下降影响更大，导致相交点提前。此外，对比N3、S3和E3可知：相同层结环境下，植被越高，异重流沿程演化过程中背景势能占总势能的比例就越小，说明异重流与环境流体间不可逆掺混引起的背景势能越不占优势。

图6 异重流无量纲总势能、背景势能和可用势能随头部位置变化关系Fig. 6 Variation of the dimensionless total potential energy, background potential energy and available potential energy with head position of gravity current

3.5 动能峰值

动能作为直接驱动异重流运动的能量来源，是异重流水平运动强烈程度的直接度量。图7给出植被区域前（P1）、后（P3）0.2 m和植被区域中间（P2）这3个特征断面处的异重流动能与时间的关系。特征断面上流体的动能[30]：

式中：Ω为积分断面；u¯和w¯分别为某时刻单位质量流体在主流方向和垂直方向上瞬时速度平均值。其中，平均值是指某一计算时刻前后各0.05 s（即0.1 s内）的平均。

图7 不同工况下异重流特征断面处动能峰值变化Fig. 7 Kinetic energy profile at the characteristic section of density currents of different cases

从图7可以看出，无植被工况N0、N1、N2（图7(a)、(d)、(e)）下在P1和P2断面处容易出现多个波峰，而P3则不会。这是因为当异重流的头部运动至P1和P2断面时，使得该断面的流体动能增大，但由于和环境流体的掺混导致浮力损失，速度下降，即出现第1个波峰。随后，异重流后方的补充流体到达该区域时，再次激活该断面处流体的动能，于是出现第2个波峰。但随着异重流流经更远的P3断面，由于和环境流体掺混较为完全，后方的流体无法及时补充头部流体，于是便不会出现多个波峰。而相同的无植被工况N3（图7(f)），由于层结度大，对异重流的掺混抑制强烈，便不足以出现产生“波谷”的浮力损失。同时，对比所有的N系工况（图7(a)、(d)、(e)、(f)）可以发现：层结环境会抑制多个波峰现象的出现，具体表现为3个特征断面处（P1、P2和P3）波峰的差值随着层结度的增大而减小，以及P3断面波峰值：N2工况＞N1工况＞N0工况（N3工况由于初始驱动力太小无法比较）。对比工况N0、S0和E0（图7(a)、(b)、(c)）可以发现：植被的存在会使异重流产生较大的速度损失，且随植被高度的增加速度损失增大，具体表现为3个特征断面波峰处的差值：E3工况＞S3工况＞N3工况。非浸没式植被工况E3在断面P1处会产生如图7(c)所示的“二次小波峰”现象，其原因为：当异重流头部刚到达植被起始边缘时，由于非浸没式植被强烈的阻力作用，速度下降明显，于是异重流后方有一小部分补充流体能够及时到达断面P1处，造成二次波峰。