风力发电机二级平行轴齿轮啮合的有限元分析

2022-03-05韦洪新王智森

南阳理工学院学报 2022年6期

韦洪新，王智森，吴云

(景德镇学院江西景德镇 333000)

0 序言

一般来说，大型的风力发电机采用一级行星齿、两级平行轴机构进行传动[1]。行星齿轮最明显的优点是具有功率分流特性，能够降低各支流传递的功率。另外，使得输出轴平行于输入轴，并且在同一直线上，能够有效减小齿轮箱的体积。由于行星齿轮传动系统具有较高的承载能力和传动比，所以被广泛应用于各种变速装置，包括增速器和减速器在内的各种大中型机械传动中[2]。风力发电机组齿轮箱输入段为行星架，经过齿轮的逐级增速，从第三级平行轴齿轮输出力矩。一般由行星轮、太阳轮、行星架和内齿轮等来组成风力发电机的行星齿轮组，在大型风力发电机中，内齿圈是固定不动，太阳轮是围绕自身的几何中心转动，而行星轮不仅围绕自身的几何中心转动，还要围绕太阳轮公转[3]。所以行星齿轮既要啮合内齿圈，又要啮合太阳轮。本文研究的风力发电机的额定功率为1.5 MW，总传动比i≈1∶88.5。其齿轮箱运动简图如图1所示。

1 模型的建立

1.1 基本参数设置

二级平行轴中大齿轮为主动轮，小齿轮为从动轮，其主动轮的齿数为100，模数为8，齿宽为180，从动轮的齿数为23，模数为8，齿宽为180，其压力角为20°，传动比≈1∶4.35。

图1 齿轮箱运动简图注：1-太阳轮，2-行星架，3-行星轮，4-内齿圈，5-三级平行轴小齿轮，6-三级平行轴大齿轮，7-二级平行轴小齿轮，8-二级平行轴大齿轮

1.2 齿轮的受力分析

齿轮的受力分析对之后的有限元分析起到决定性的作用[4]。为了减少不必要的受力分析，假定各级齿轮受到的载荷均匀，忽略摩擦力和重力，在齿轮组中二级平行轴齿轮与三级平行轴齿轮受力的类型是一样的，图2为二级齿轮受力分析图。

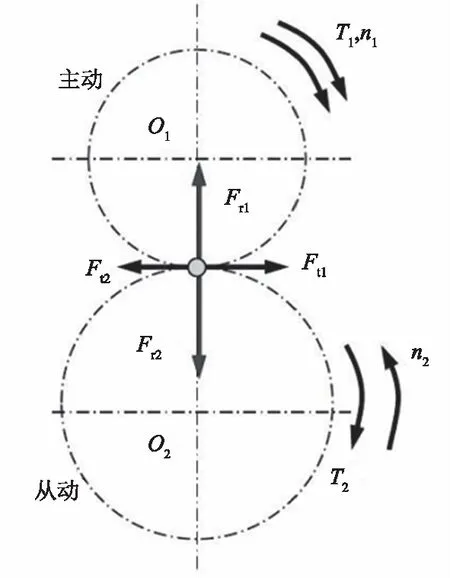
图2 二级平行轴齿轮受力分析

在机械设计中齿轮受力分析可知，轴传递的转矩

(1)

齿轮的圆周力

(2)

齿轮的径向力

(3)

齿轮的轴向力

Fa=Fttanβ

(4)

以上式中：α为法面压力角；β为螺旋角；d为节圆直径；Fr为径向力；Fa为轴向力[5]。

由风力发电机齿轮原始数据，经过实际计算可得到各个齿轮的受力分析结果如表1所示。

表1 各齿轮受力分析结果

1.3 有限元建模

在做齿轮有限元分析前需要建立齿轮的三维模型，同时对齿轮基本的受力进行分析，确保所建立的模型没有干扰或不确定的区间[6]。先利用UG建立齿轮的三维模型，建立后选中三维模型，在文件中导出选择Parasoild文本文件即“X_T”文件格式，将其导入ANSYS进行数据计算和分析。齿轮用的材料为20CrMnMo，屈服强度为1180 MPa，抗拉强度为885 MPa，泊松比为0.254，弹性模量为2.07×108GPa，密度为7870 kg/m3。

在ANSYS Workbench 环境下网格的划分，网格划分是有限元结构分析关键的一步，网格划分具有原则性，一是要保证计算精度，二是要具有一定的效率。网格划分精度越高，其计算精度也越高，随着精度提高，带来的是计算量大幅度增加，如果计算量过大，会导致计算求解自动终止。在本次分析中自动划分网格可以满足设计要求，故选择Generate Mesh生成网格。其二级齿轮的有限元模型如图3所示，共生成16260个单元，86460个节点。

图3 二级齿轮的有限元模型

2 齿轮静态和模态分析

2.1 静态分析

为了保证计算结果更精确，给两个齿轮分别加上只能绕Z轴旋转的约束，之后在二级齿轮有限元模型主动轮和从动轮间施加力和力矩, 施加力的大小已在表1中列出，最后求解，得出二级齿轮的位移分布如图4所示，应变分布如图5所示，应力分布如图6所示。

图4 二级齿轮位移分布云图

图5 二级齿轮应变分布云图

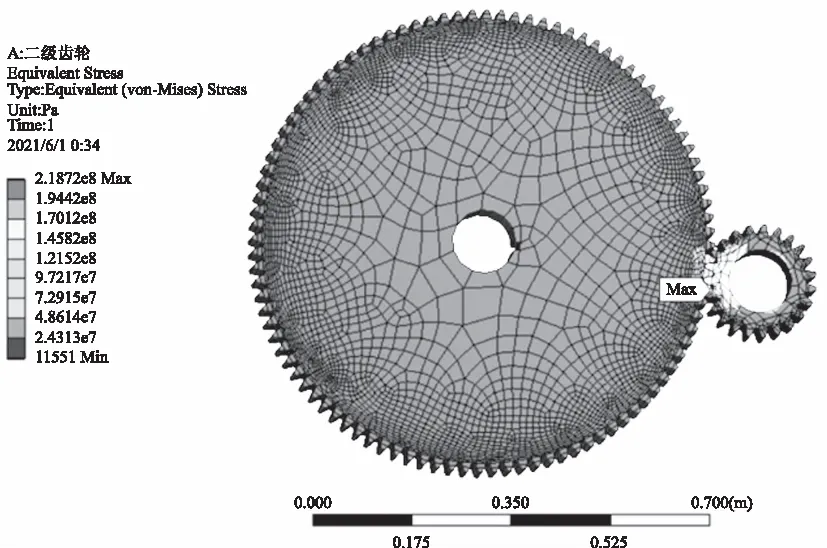
图6 二级齿轮应力分布云图

从图4可知最大变形为0.20 mm，从图5和图6中可以看出，二级齿轮应力最大值为218.72 MPa，20CrMnMo材料的屈服许用应力为1180 MPa，抗拉许用应力为885 MPa，二级齿轮的最大应力远远小于材料的屈服极限应力值，即使考虑应力集中的情况，二级齿轮强度依然满足要求。

通过模拟计算分析可知，当二级齿轮仅有静力载荷作用下，齿轮的强度是足够的。由于在实际的工作中，齿轮还受到外部载荷的影响，如齿轮箱振动冲击载荷等，在复杂多轴载荷瞬时冲击作用下，二级齿轮会产生共振。仅分析静态特性是不够的，因此需要对二级齿轮进行模态分析，分析该结构在易受影响的频率范围内的模态特性，预测该结构在各种振动源下产生的振动响应。

2.2 模态分析

模态分析主要用于确定结构的振动特性，不随载荷发生改变，用它可以确定结构的振型和固有频率。模态分析是将线性定常系统振动微分方程组解耦，从计算的角度上讲，模态分析是通过求解特征值和模态变换方程，将耦合运动方程变换到模态空间的一个过程[7]。模态分析的最终目的是获得阻尼、振型和频率等模态参数。为后续结构动态设计、设备故障预测与诊断提供指导和参考。

在导入ANSYS Workbench的模型中基本的参数不变，利用Model模块对其网格进行重新划分：二级齿轮共有16260个单元，86460个节点。再添加约束，分别对齿轮的径向自由度进行约束，对于行星齿轮需要对内齿圈进行全约束求解，得到不同齿轮的不同振型下的固有频率值(见表2)。

表2 二级齿轮的前十阶啮合状态下的固有频率

图7至图10是不同阶次的振型图，由于篇幅的原因，只取其中的几阶振型图附上。

图7 一阶振型图

图8 三阶振型图

图9 七阶振型图

图10 九阶振型图

根据前十阶振型图可知，在1阶振动时，沿小齿轮圆心向外膨胀；2、3、4、5、8、9、10阶时，大齿轮前后摆动；6阶时，大齿轮上下移动，沿齿轮圆心向外膨胀；7阶时，大齿轮左右移动。对于风力发电机，发电机转速一般为3000 r/min，振动频率为50 Hz，齿轮在受扭作用下的一阶频率为259.6 Hz。综合分析，齿轮与发电机的频率没有重叠，不会产生共振，满足设计需要。