一类含有两个(n-1)-圈的三色有向图本原指数

罗美金, 卢钰松, 韦玉程

(河池学院 数理学院, 广西 宜州 546300)

1 预备知识

若D是包含红弧、黄弧和蓝弧的有向图，则称D是一个三色有向图.若D中每一对顶点(i,j)都存在从i到j的途径，则称D是强连通的.给定D中的一条途径ω，若用r(ω)，y(ω)和b(ω)分别表示ω中红弧、黄弧和蓝弧的数目，称ω为一条(r(ω),y(ω),b(ω))-途径，则ω这条途径的分解是向量(r(ω),y(ω),b(ω))或(r(ω),y(ω),b(ω))T[1].

一个三色有向图D是本原的，当且仅当存在非负整数h，k和v，且h+k+v>0，使得D中的每一对顶点(i,j)都存在从i到j的(h,k,v)-途径，h+k+v的最小值即为三色有向图D的本原指数，记为exp(D)[1].

设C={γ1,γ2,…,γl}是D的圈集合，定义D的圈矩阵M是一个3×l矩阵，它的第i列是γi的分解.M的content(记为content(M))定义为0如果M的秩小于3，否则定义为M的所有非零3阶主子式的最大公因数[2].

引理1[2]一个至少包含一条红弧、一条黄弧和一条蓝弧的三色有向图D是本原的，当且仅当D是强连通的，且content(M)=1.

非负本原矩阵簇指数的研究是矩阵组合理论中一个崭新的研究课题，是非负本原矩阵对指数问题的深化，更是单个非负矩阵概念的推广，是国内外研究的热点问题.当前，关于传统单个非负本原矩阵、本原矩阵对的指数已经取得了不少成果[1,3-4]，而对于具有代表性的非负本原矩阵簇指数的研究因情况复杂，可能性多，计算量大等因素造成大部分问题都未得到解决，成果甚少[2,5-9].

本文将非负矩阵簇与其伴随有向图建立关系，在文献[6]的基础上，进一步讨论至少包含一条红弧、一条黄弧和一条蓝弧的三色有向图D，给出了a=c时的本原情况，并借助maple计算指数上界及刻画极图.该三色有向图D的未着色图如图1所示.

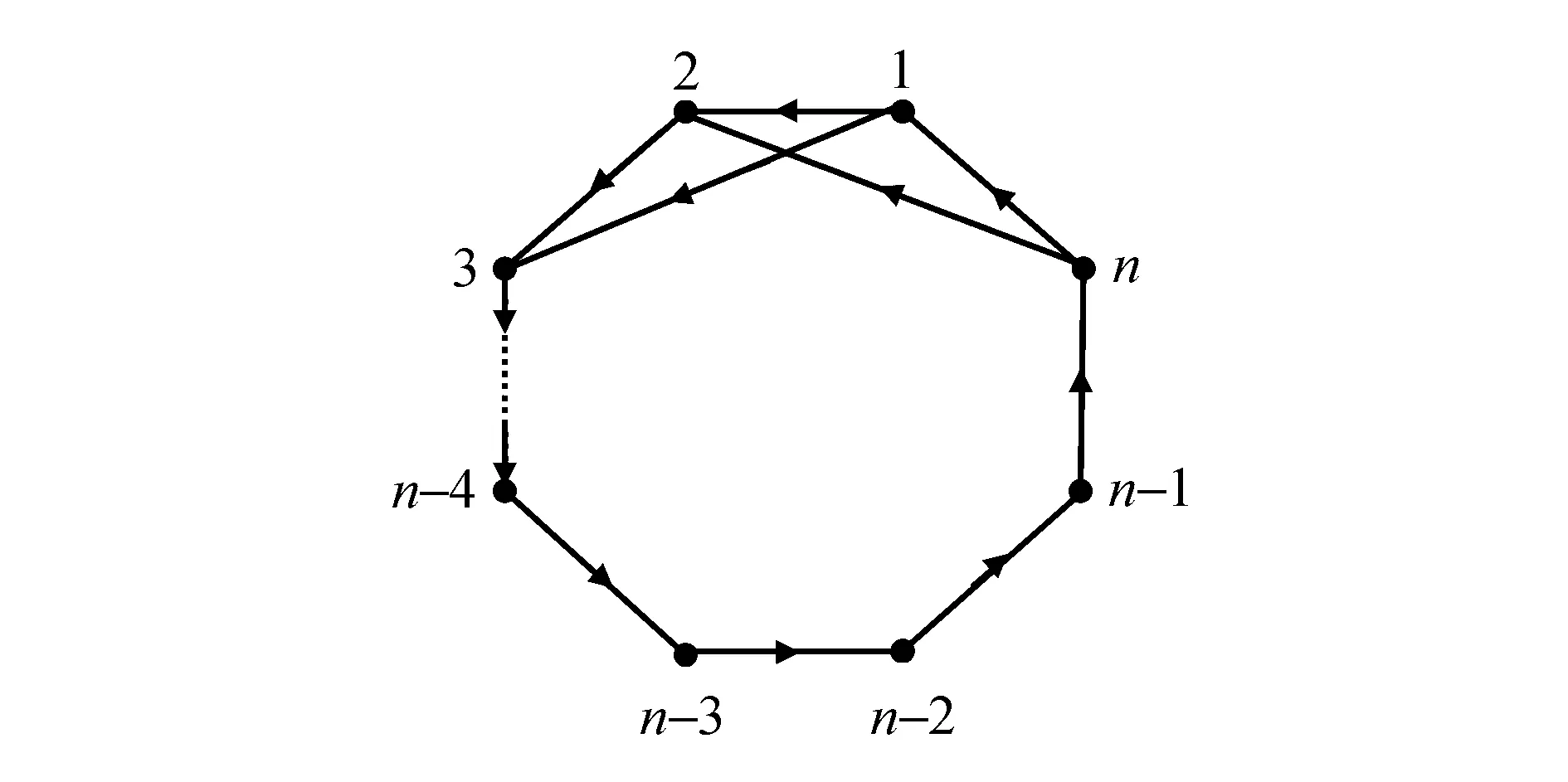
图1 未着色有向图DFig.1 Uncolored digraph of D

由图1可知，D中含有n(n≥3)个顶点，一个n-圈和两个(n-1)-圈，且三圈有一条n-3长的公共弧3→4→…→n.不妨设D的圈矩阵为

(1)

式中:a，b，c，d，e，f都为非负整数，且a，b，c，d，e，f满足关系式：

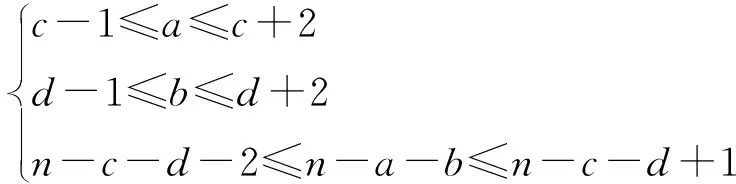
(2a)

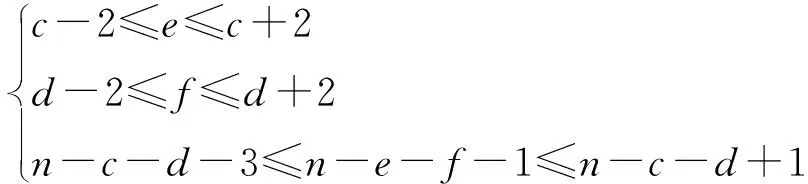
(2b)

2 a=c时的本原条件

定理1若a=c，b=d-1时，三色有向图D是本原的，当且仅当x=0，y=±1，c=1.

证明由图1可知D是强连通的.不防设e=c+x,f=d+y，代入式(2a)和式(2b)则有-2≤x≤2，-2≤y≤2，-2≤x+y≤2.若a=c，b=d-1时，结合式(1)有c+d≤n-1，det(M)=x(-n-d+1)+cy.由引理1可得，D是本原的当且仅当content(M)=1，即x(-n-d+1)+cy=±1.分以下5种情况讨论D在a=c，b=d-1时的本原情况：

1) 若D是本原的，且x=-2，则c≥2，0≤y≤2，-2(-n-d+1)+cy=±1.容易验证，y=0或2时，-2(-n-d+1)+cy为偶数；y=1时，-2(-n-d+1)+c=2n+2d+c-2>1；显然-2(-n-d+1)+cy≠±1.故x=-2时，D是不本原的.

2) 若D是本原的，且x=-1，则c≥1，-1≤y≤2，-(-n-d+1)+cy=±1.容易验证，y=-1或0或1或2时，-(-n-d+1)+cy=n+d-1+cy>1；显然-(-n-d+1)+cy≠±1.故x=-1时，D是不本原的.

3) 若D是本原的，且x=0，则c≥0，-2≤y≤2，cy=±1.容易验证，y=-2或0或2时，cy为偶数；y=±1时，则必有c=1成立.故x=0，y=±1，c=1时，D是本原的.

4) 若D是本原的，且x=1，则c≥0，-2≤y≤1，-n-d+1+cy=±1.容易验证，y=-2或-1或0或1 时，-n-d+1+cy<-1；显然-n-d+1+cy≠±1.故x=1时，D是不本原的.

5) 若D是本原的，且x=2，则c≥0，-2≤y≤0，2(-n-d+1)+cy=±1.容易验证，y=-2或-1或0时，2(-n-d+1)+cy<-1；显然2(-n-d+1)+cy≠±1.故x=2时，D是不本原的.

综上所述，若a=c，b=d-1时，三色有向图D是本原的，当且仅当x=0，y=±1，c=1.定理得证.

类似定理1的证明，可得定理2～定理4.

定理2若a=c，b=d时，三色有向图D是本原的，当且仅当满足以下条件之一:

1)x=y=-1，d-c=±1；

2)x=-1，y=0，d=1；

3)x=-1，y=c=1，d=0；

4)x=0，y=±1，c=1；

5)x=d=1，y=-1，c=0；

6)x=d=1，y=0；

7)x=y=1，c-d=±1.

定理3若a=c，b=d+1时，三色有向图D是本原的，当且仅当满足以下条件之一:

1)x=-1，y=1，c+d=n-2；

2)x=-1，y=0，c=1，d=n-2；

3)x=-1，y=2，-n+d+2c+1=±1；

4)x=0，y=±1，c=1；

5)x=1，y=-2，n-d-2c-1=±1；

6)x=1，y=-1，c+d=n-2；

7)x=1，y=0，c=0，d=n-2.

定理4若a=c，b=d+2时，三色有向图D是本原的，当且仅当x=0，y=±1，c=1.

3 指数上界

以下对定理1～定理4中的所有本原情况，分别讨论找到对应的指数上界，将所得指数上界进行比较，找到所有本原情况下，a=c，b=d，x=y=1，c-d=±1时，D的本原指数最大.以下只给出a=c，b=d，x=y=1，c-d=±1时的指数上界证明过程，其他本原情况不再赘述.

定理5若三色有向图D是本原的，且a=c，b=d，x=y=1，c-d=±1，则

证明对任意的顶点(i,j)，记pij是从i到j的最短路r(pij)=s，y(pij)=t，b(pij)=w.分a=c，b=d，x=y=1，c-d=1和a=c，b=d，x=y=1，c-d=-1两种情况讨论D的本原指数上界.

1) 当a=c，b=d，x=y=1，c-d=1时

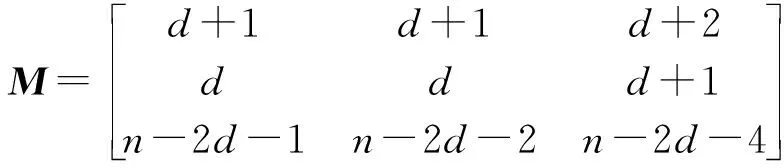
只需证明对D的任意一对顶点y都有一((d+1)(nd+2n-2d-4)+(d+1)(nd+d2+2n+d-2)+(d+2)(d2+2d+1)，d(nd+2n-2d-4)+d(nd+d2+2n+d-2)+(d+1)(d2+2d+1)，(n-2d-1)(nd+2n-2d-4)+(n-2d-2)(nd+d2+2n+d-2)+(n-2d-4)(d2+2d+1))-途径.取ρ1=nd+2n-2d-4+(n-2)s-nt-w，ρ2=nd+d2+2n+d-2-(n+d-1)s+(n+d+2)t+w，ρ3=d2+2d+1+ds-(d+1)t.因此，从顶点i出发，沿pij到顶点j，转n-圈ρ1次，转其中一个(n-1)-圈ρ2次，转另一个(n-1)-圈ρ3次的途径有分解

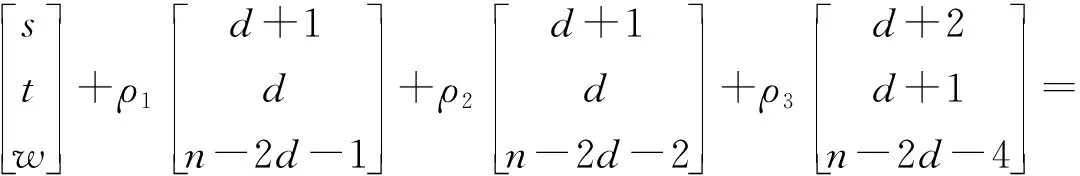
此时，结合图1，可得0≤s≤d+2，0≤t≤d+1，0≤w≤n-2d-1.当s=d+2时，t≥0，w≥0；当t=d，w=n-2d-1或t=d，w=n-2d-2或t=d+1，w=n-2d-4时，s≥0;当w=n-2d-2或w=n-2d-1时，pij至少转其中一个(n-1)-圈1次.容易验证，ρ1≥0，ρ2≥0，ρ3≥0.所以，

exp(D)≤(d+1)(nd+2n-2d-4)+(d+1)×

(nd+d2+2n+d-2)+(d+2)(d2+

2d+1)+d(nd+2n-2d-4)+d(nd+d2+2n+d-2)+(d+1)(d2+2d+1)+

(n-2d-1)(nd+2n-2d-4)+(n-

2d-2)(nd+d2+2n+d-2)+(n-

2d-4)(d2+2d+1)=n(nd+2n-2d-4)+(n-1)(nd+d2+2n+d-2)+

(n-1)(d2+2d+1)

显然，exp(D)是关于d的函数，利用maple对上式合并计算得

exp(D)≤2dn2+4n2+2d2n-2d2-7n-3d+1

对exp(D)关于变量d求导得

exp′(D)=2n2+4nd-4d-3

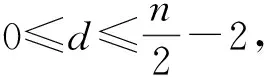
2) 当a=c，b=d，x=y=1，c-d=-1时

只需证明对D的任意一对顶点(i,j)都有一((d-1)(nd-2d+n-2)+(d-1)(nd+d2+n-d-2)+d3，d(nd-2d+n-2)+d(nd+d2+n-d-2)+(d+1)d2，(n-2d+1)(nd-2d+n-2)+(n-2d)(nd+d2+n-d-2)+(n-2d-2)d2)-途径.取ρ1=nd-2d+n-2-ns+(n-2)t-w，ρ2=nd+d2+n-d-2+(n+d+1)s-(n+d-2)t+w，ρ3=d2-ds+(d-1)t.因此，从顶点i出发，沿pij到顶点j，转n-圈ρ1次，转其中一个(n-1)-圈ρ2次，转另一个(n-1)-圈ρ3次的途径有分解如下：

此时，结合图1，可得0≤s≤d，0≤t≤d+1，0≤w≤n-2d+1.当t=d+1时，s≥0，w≥0；当s=d-1，w=n-2d+1或s=d-1，w=n-2d或s=d，w=n-2d-2时，t≥0；当s=d，w=n-2d+1或w=n-2d时，pij至少转其中一个(n-1)-圈1次.容易验证，ρ1≥0，ρ2≥0，ρ3≥0.所以，

exp(D)≤(d-1)(nd-2d+n-2)+(d-1)×

(nd+d2+n-d-2)+d3+d(nd-

2d+n-2)+d(nd+d2+n-d-2)+(d+1)d2+(n-2d+1)(nd-2d+n-2)+(n-2d)(nd+d2+n-d-2)+

(n-2d-2)d2=n(nd-2d+n-2)+

(n-1)(nd+d2+n-d-2)+(n-1)d2

显然，exp(D)是关于d的函数，利用maple对上式合并计算得

exp(D)≤2dn2+2n2+2d2n-2d2-

4dn-5n+d+2

对exp(D)关于变量d求导得

exp′(D)=2n2+4nd-4d-4n+1

因0≤d≤n/2-1，则exp′(D)>0，exp(D)在闭区间[0，n/2-1]上为增函数，因此

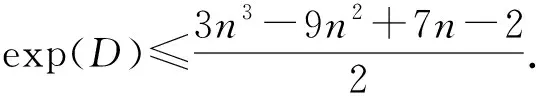
其他本原情况，寻找指数上界的方法与a=c，b=d，x=y=1，c-d=±1时相同，证明过程相似，故只给出结果不再赘述.当a=c时，三色有向图D的所有本原情况和本原指数上界，见表1所列.

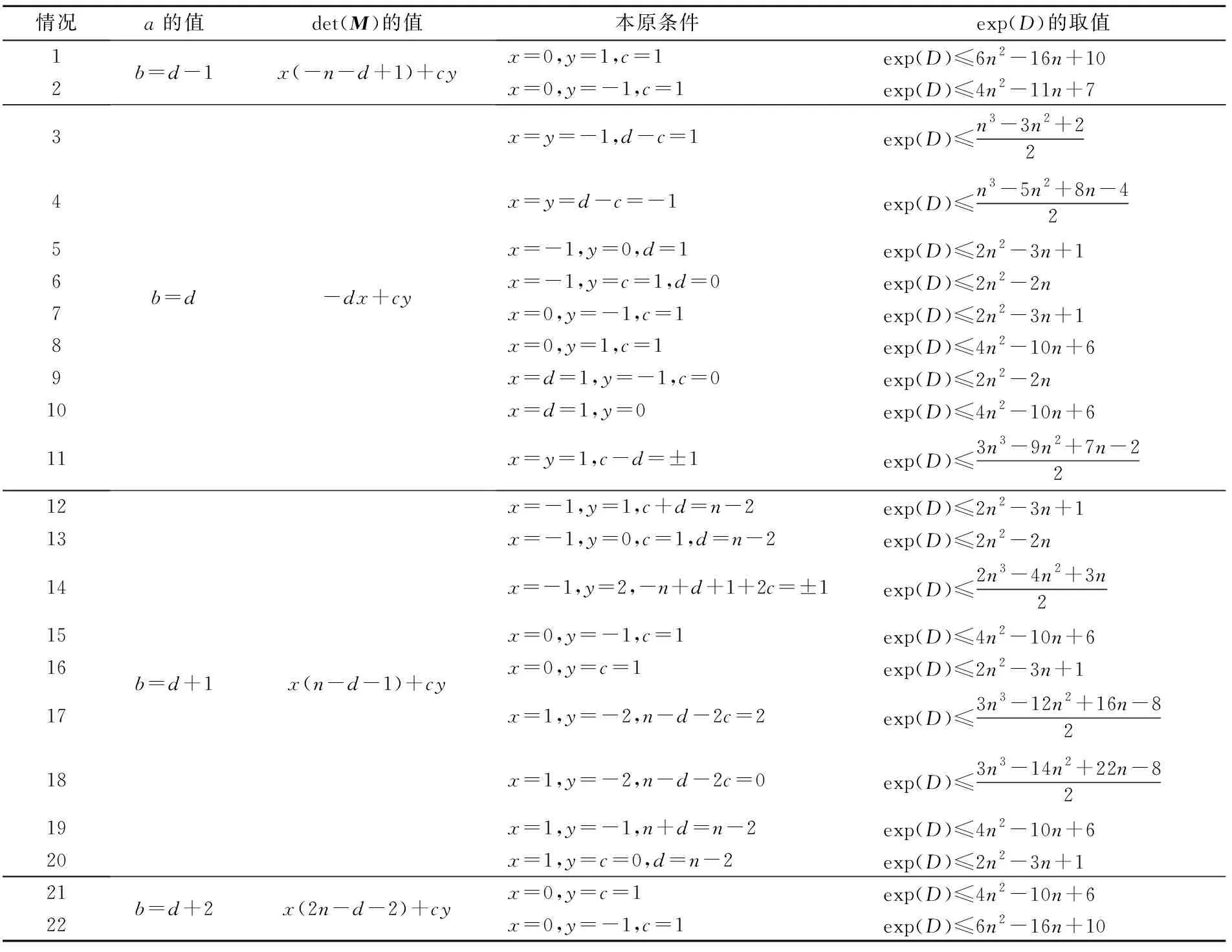
表1 a=c时，D的本原条件和指数上界

4 极图刻画

定理6若a=c，b=d，x=y=1，c-d=1时，三色有向图D是本原的，则

当且仅当D中恰有d+2长的连续红路.

证明充分性) 结合定理5，要证明

exp(D)=n(nd+2n-2d-4)+(n-1)(nd+

d2+2n+d-2)+(n-1)(d2+2d+1)

只需证明

exp(D)≥n(nd+2n-2d-4)+(n-1)(nd+d2+2n+d-2)+(n-1)(d2+2d+1)

即可.

设存在一对非负整数(h，k，v)，使对D中所有顶点对(i,j)，都有一条从i到j的(h，k，v)-途径.取i=j=n，则存在非负整数u1，u2和u3，使得

结合图1，不难发现三色有向图D若存在d+2长的连续红路，则d+2长的连续红路必在(n-1)-圈上.取i，j分别为d+2长连续红路的起点和终点，则从i到j的路分解为(d+2，0，0)，因此

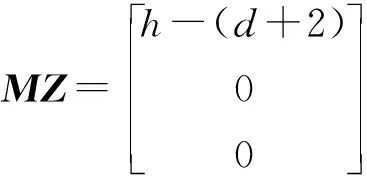
有非负整数解，即

故u2≥nd+d2+2n+d-2.

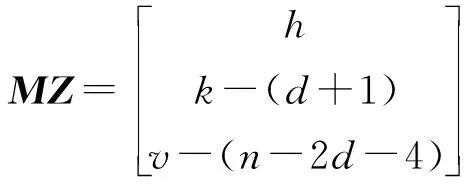
故u1≥nd+2n-2d-4，u3≥d2+2d+1.从而

所以

exp(D)≥n(nd+2n-2d-4)+(n-1)(nd+d2+2n+d-2)+(n-1)(d2+2d+1)

必要性) 若三色有向图D是本原的，D中不存在d+2长的连续红路，只需证明exp(D)

对D中的任意一对顶点(i,j)都有一((d+1)(nd+n-2d-2)+(d+1)(nd+d2+2n+d-3)+(d+2)(d2+2d+1)，d(nd+n-2d-2)+d(nd+d2+2n+d-3)+(d+1)(d2+2d+1)，(n-2d-1)(nd+n-2d-2)+(n-2d-2)(nd+d2+2n+d-3)+(n-2d-4)(d2+2d+1))-途径.取ρ1=nd+n-2d-2+(n-2)s-nt-w，ρ2=nd+d2+2n+d-3-(n+d-1)s+(n+d+2)t+w，ρ3=d2+2d+1+ds-(d+1)t.因此，从顶点i出发，沿pij到顶点j，转n-圈ρ1次，转其中一个(n-1)-圈ρ2次，转另一个(n-1)-圈ρ3次的途径有分解

此时，结合图1，可得0≤s≤d+2，0≤t≤d+1，0≤w≤n-2d-1.当s=d+2时，t≥1或w≥1；当s≤d+1时，t≥0且w≥0；当t=d+1，w=n-2d-4时，s≥1.容易验证，ρ1≥0，ρ2≥0，ρ3≥0.所以，

exp(D)≤(d+1)(nd+n-2d-2)+(d+1)(nd+

d2+2n+d-3)+(d+2)(d2+2d+1)+

d(nd+n-2d-2)+d(nd+d2+2n+

d-3)+(d+1)(d2+2d+1)+(n-

2d-1)(nd+n-2d-2)+(n-2d-2)×

(nd+d2+2n+d-3)+(n-2d-4)×

(d2+2d+1)=n(nd+n-2d-2)+

(n-1)(nd+d2+2n+d-3)+

(n-1)(d2+2d+1)

2d-4)+(n-1)(nd+d2+2n+

d-2)+(n-1)(d2+2d+1)

因此，a=c，b=d，x=y=1，c-d=1时，若D中不存在d+2长的连续红路，则

exp(D)

(nd+d2+2n+d-2)+(n-1)(d2+2d+1)

结合定理5，定理得证.

类似定理5、定理6的证明，可得定理7.

定理7若a=c，b=d，x=y=1，c-d=-1时，三色有向图D是本原的，则

exp(D)=n(nd-2d+n-2)+(n-1)×

(nd+d2+n-d-2)+(n-1)d2

当且仅当D中恰有d+1长的连续黄路.