板状结构Lamb波频散补偿与聚焦接收成像检测∗

阚婷婷 阎守国 张碧星

(1 中国科学院声学研究所 北京 100190)

(2 中国科学院大学 北京 100049)

0 引言

板状结构在航空航天、民生设施中的应用越来越广泛。这些板状结构在生产制造以及使用过程中会出现疲劳、裂纹等损伤，这存在极大的安全隐患。为了确保工程结构的安全稳定，避免经济财产的损失以及灾难事故的发生，对板状结构进行无损检测是非常重要的[1−5]。

超声导波具有传播距离远、衰减小、对微小损伤敏感的特性，非常适用于大型板状结构的无损检测。因此，很多基于导波的成像方法被发掘出来，如时间反转法[6]、拓扑成像法[7]、频域波束形成[8]等。这些方法大部分是从传统体波检测的成像方法中转移过来的，但是由于导波的频散和多模式限制，通常选择低频窄带的单一模式导波检测方法，因此限制了Lamb 波在结构缺陷检测中的应用。对于导波频散的克服方法，目前一般可采用时间反转法或主动相位补偿的方法来实现。Ing 等[9]首先使用时间反转镜技术补偿了Lamb 波的频散效应，实现了Lamb波的聚焦和板内缺陷的检测。张海燕等[10]结合时间反转法，使用分布式传感器网络对铝板中存在的缺陷进行检测与成像。近年来随着对导波频散特性的深入研究，学者们提出一种主动消除频散的方法。Sicard 等[11]提出一种频域频散补偿算法，在频率域结合频散曲线和传播距离，调节每个频率分量的相位，实现钢板的导波信号频散补偿及损伤检测。Xie 等[12]提出了单一模式导波聚焦方法，以及一种基于虚拟时间反转的宽频带多模式导波聚焦的方法。对于导波的多模式问题，陈晓等[13]提出一种分数阶微分理论，实现了对时频重叠的S1模式和A1模式信号的分离。许凯亮等[14]提出了基于时频分析的导波多模式分离和重建算法，实现多模式导波的分离。以上工作主要是为了实现导波聚焦发射的过程，应用聚焦导波对结构进行扫描，从而提高对缺陷的检测能力。对于缺陷散射的导波在传到换能器后又发生了频散与模式转换的问题，常规成像算法通常只提取某一模式的导波信号进行成像，而忽略了模式转换之间蕴含的有用信息，并且未考虑接收过程中的频散，造成了成像分辨率的不足。

针对这一问题，本文在理论分析的基础上，结合有限元仿真方法，对与缺陷作用后的回波信号进行聚焦接收处理，提出一种基于频散补偿的缺陷定位成像算法，并利用该方法对二维和三维模型板中的缺陷进行检测成像，验证了此方法的有效性。

1 Lamb波频散补偿理论

Lamb 波是指在上下表面自由的板中传播的波，是由边界及纵横波经过多次反射所耦合出来的。对于厚度为2h的各向同性的板，频散方程[15]表示为

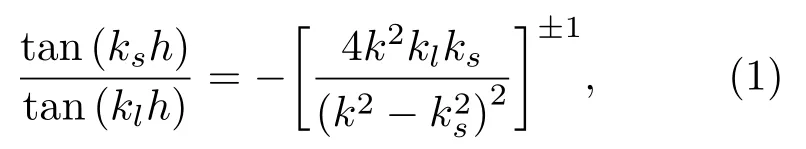
其中：k=ω/cp，k2l=ω2/v2l −k2，k2s=ω2/v2s −k2。式中k为波数，ω为角频率，cp为板的相速度，vl和vs分别为板的纵波速度和横波速度。式(1)中右上角取+1时代表对称模式，取−1时代表反对称模式。对式(1)求解得如图1所示导波相速度cp和群速度cg的频散曲线，模型参数如表1所示。

表1 模型参数Table 1 The parameters of model

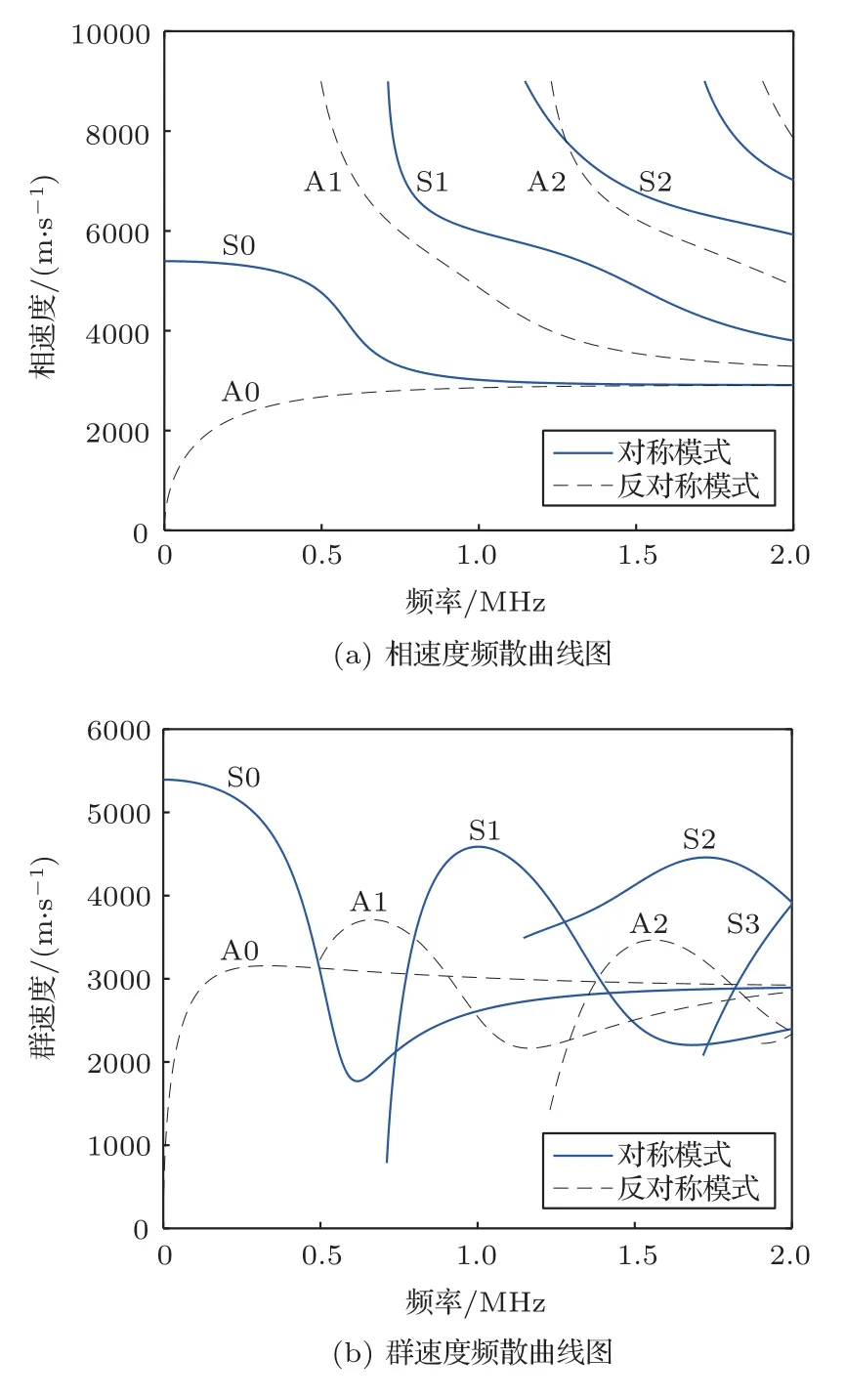
图1 铝板频散曲线图Fig.1 Dispersion curves for aluminum

从图1所示的频散曲线可以看出，不同频率的波传播速度是不同的，缺陷回波信号从缺陷传播到接收点时会发生频散。设在接收点x处接收的缺陷回波信号为r(x,t)，运用傅里叶变换将其变换到频率域可表示为

其中，t为时间，其中缺陷相当于一个被动声源位于坐标原点O处，x表示缺陷与接收点之间的距离，记录与缺陷作用后缺陷处的信号为S(0,ω)。为了方便说明频散补偿求解过程，先假设缺陷回波中只包含一个模式，R(x,ω)可表示为

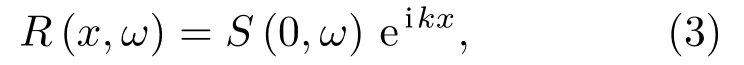
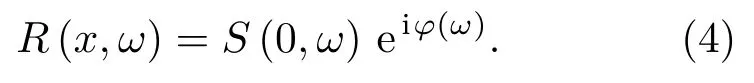
由相速度的频散方程可知导波的相速度cp是随频率f的变化而变化的，在式(4)中，当x≠0 时，不同频率的波的相移便不同，并且随着x的增加，相位差就越大，变到时域波形将会展开，导致能量不集中。在已知导波频散特性和导波传播距离的基础上，相位因子φ(ω)是可以通过计算得到的。通过引入补偿因子−φ(ω)，就能够对不同频率的波进行频散补偿，对接收信号R(x,ω)施加频散补偿后得

不同频率的波经频散补偿后相位是相同的，对式(5)进行反傅里叶变换得到聚焦接收信号rf(t)为

经过频散补偿后，缺陷散射信号变为O位置处未发生频散的信号。

2 多模式Lamb波信号的聚焦接收

在应用Lamb 波进行板状结构的缺陷检测时，在给定的频率下至少存在两个模式(A0 模式和S0模式)在板中传播，如图1所示。实际应用中为了避免导波的频散和多模特性，降低信号分析难度，通常在低频范围选择性激发单一模式的Lamb 波(如S0模式)，但是当Lamb 波与缺陷相互作用时，会发生模式转换现象，因此Lamb 波检测时频散和多模式现象不可避免，为了提高缺陷检测的精度，本文提出对缺陷的多模式回波信号进行聚焦接收处理。

假设回波信号中包含两个模式，即

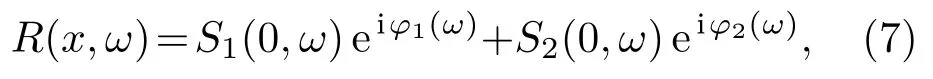
其中，φ1(ω)和φ2(ω)分别为两个模式的相位因子。与单模式频散补偿类似，引入频散补偿因子−φ1(ω)和−φ2(ω)，由式(7)可得

其中，Δφ(ω)=φ1(ω)−φ2(ω)，反傅里叶变换到时域得

其中，前两项s1和s2表示得到完全频散补偿的两个模式，s′1、s′2表示未被完全补偿的干扰项。前两项时域上恢复为原始无频散形式，应用窗函数截取O位置处的信号，得到聚焦接收信号：

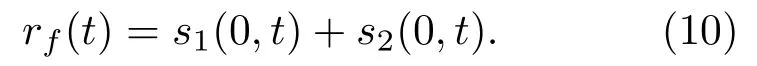
当回波信号中包含多个模式时，可采用同样的方法引入补偿因子后截取即可得到聚焦接收信号。

在缺陷检测时，声波遇到缺陷发生了反射，在接收点接收到缺陷回波信号，通常接收点与缺陷之间的距离x是未知的，在对接收的缺陷回波信号进行频散补偿时，应用预设相位来对信号进行补偿，x′为该相位对应的传播距离，式(5)改写为

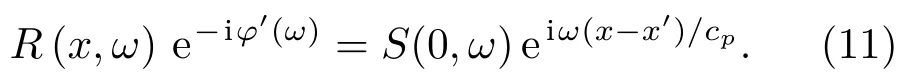
从式(11)中可以看到，当x′=x时，频散的波得到完全频散补偿，对应得到的rf(t)的峰值将达到最大。当回波信号中包含两个模式时，采用类似的补偿方法，将对缺陷的定位问题转化为寻找补偿后信号的峰值问题，当信号补偿的距离等于缺陷与换能器之间的实际距离时，信号的峰值达到最大。

应用有限元软件对含有缺陷的铝板进行模拟，二维板状模型如图2所示，设置铝板的长度为2 m，厚度为0.004 m，材料参数如表1所示。在板中心位置上下表面施加法向力源，以此激发Lamb 波的对称模式，激励信号为5 个周期汉宁窗调制的正弦波，中心频率为250 kHz。在距离激励源0.5 m 处设置凹槽类缺陷，缺陷大小为2 mm×2 mm。接收点位于铝板上表面，分别距离激发点0.2 m、0.3 m、0.4 m、0.5 m。

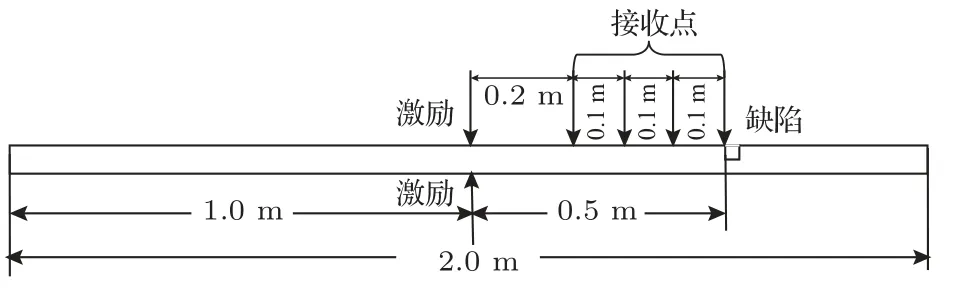
图2 计算模型示意图Fig.2 Diagram of simulation model

为了保证计算的精度和速度，网格的划分也是一个重要的环节。通常网格的尺寸应小于最小激励模式波长的1/10，对应的时间步长应小于速度最快的模式导波通过一个网格所用的时间。依据此标准，在声源中心频率为250 kHz时，设置网格大小为0.5 mm，时间步长为20 ns。

图3为各个接收点接收到的时域波形，其中第一个波包为直达波，后面的波包为与缺陷作用后的散射回波。由波速法判定导波的模式，计算得到第一个波包的速度为5040 m/s，与S0 模式的理论群速度5119 m/s 接近，故对称方式激励时，板中只存在S0 模式。在与缺陷作用后，缺陷回波在传播过程中发生模式转换，分为两个波包，计算波包的速度分别为5025 m/s 和3024 m/s，分别对应为S0 模式和A0 模式(A0 模式理论群速度3137 m/s)。当接收点与缺陷的距离逐渐增大时，缺陷回波信号在时间上不断被拉长，并且由于频散效应，每个波包也被拉长，幅值降低，在实际检测过程中将增加信号分析过程中的难度，接着截取在0.2 m 处接收的缺陷回波进行频散补偿处理。

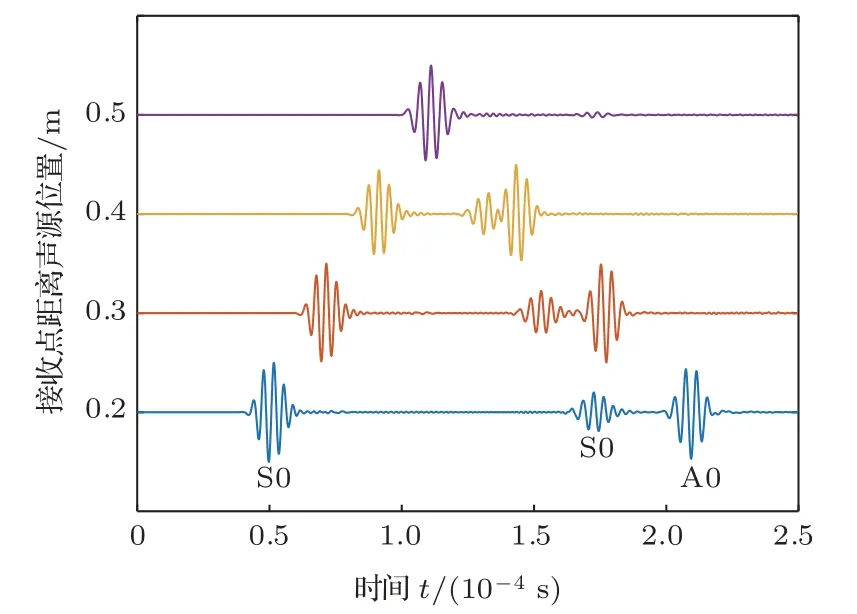
图3 不同位置的时域波形Fig.3 Temporal waveforms at different locations

应用公式(8)的方法对回波信号中的两个模式进行频散补偿，补偿后的结果如图4(a)所示，其中下方蓝色曲线是截取的缺陷回波信号，上方黑色曲线是对频散补偿后的结果。虚线中截取的是经过完全频散补偿的两个模式的叠加信号，对应公式(9)中的前两项信号，第一个波包和第三个波包分别对应公式(9)中的s′1和s′2，是频散没有被完全补偿的干扰项，截取O位置处的信号得到聚焦接收信号，如图4(b)中红色曲线所示。聚焦接收处理克服了导波检测中的频散和模式转换现象，信号在时域上的持续时间由原来的61 µs 减少到23 µs，在幅度上聚焦接收信号的峰值是普通接收信号峰值的1.938倍，从图中也可以明显看出聚焦效果是比较好的。

从以上的分析中可知，当两个模式的信号得到完全频散补偿时，信号的峰值将达到最大。在应用缺陷回波信号对缺陷进行定位时，通过在一定距离范围内对信号进行频散补偿，寻找补偿后信号峰值达到最大时对应的补偿距离即为缺陷与传感器的实际距离。

应用图4(a)中的在距离缺陷0.3 m 接收的回波数据来判断缺陷位置，结合图1中群速度频散曲线以及声源的中心频率，判断缺陷的位置在0.1～0.5 m 的范围内，以0.001 m 的间隔递增按照聚焦接收的方法对信号进行频散补偿，得到补偿后信号幅值的最大值随补偿距离x的变化如图5所示，随着补偿距离的增加，信号的峰值整体上先逐渐增大，在x=0.297 m时达到最大值，随后又逐渐减小。由此得到缺陷与接收点的距离为0.297 m，实际上缺陷距离接收点0.3 m，误差为1%，在误差允许的范围内。

图4 导波聚焦接收Fig.4 Focused reception of guided waves

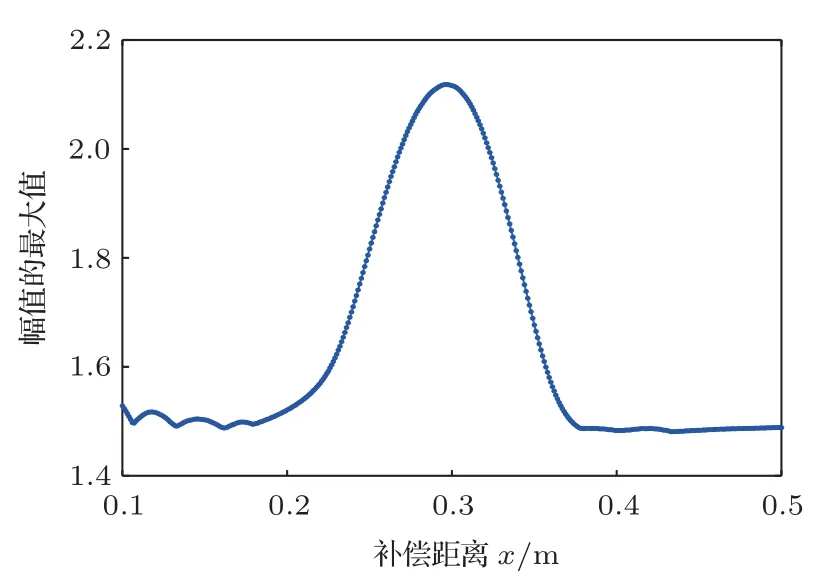
图5 幅值的最大值与补偿距离关系曲线Fig.5 Relationship between maximum amplitude and compensation distance

为了验证此方法的有效性，分别在距离接收点0.2～0.8 m 的范围内，每隔0.1 m 设置一个缺陷进行有限元模拟。对得到的回波数据进行补偿从而对缺陷位置进行定位，计算结果如表2所示，误差范围都在2%以内，结果是比较准确的。通过频散补偿，将补偿后信号的峰值达到最大时对应的补偿距离视为计算得到的缺陷位置，利用这个方法可以对缺陷位置进行准确判断。

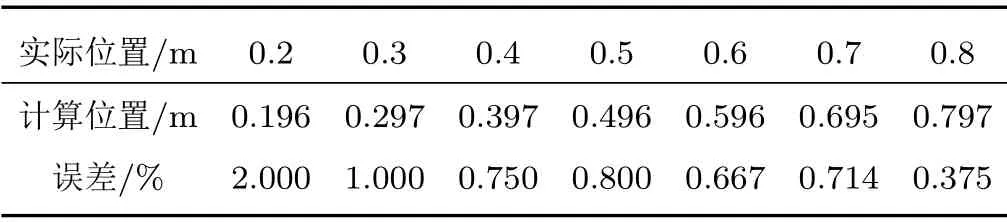
表2 缺陷计算位置及实际位置Table 2 The calculated location and actual location of defects

3 缺陷成像算法

三维模型中，信号不再以平面波形式传播，而是以柱面波形式传播，当声传播距离远大于波长时，公式(3)可改为

其中，r表示缺陷与接收点之间的距离，在对信号进行归一化处理后分析过程与平面波的处理一样。通过频散补偿的方法可以找到缺陷与接收点之间的距离，根据得到的距离提出一种基于频散补偿的缺陷检测算法。在对三维板中缺陷进行定位时，传感器布置和缺陷位置如图6所示，对感兴趣的缺陷区域布置N个传感器，Lamb 波经其中一个传感器激励，与缺陷相互作用后产生的缺陷回波被各个传感器接收，将带有缺陷板与健康板中测得的信号做差来获取缺陷散射信号。应用聚焦接收的方法计算得到接收传感器与缺陷的距离，提出基于频散补偿的缺陷成像算法：

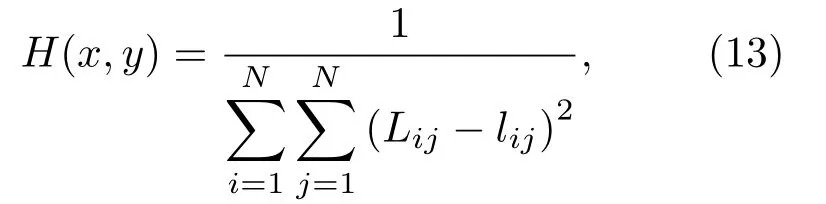
其中，H(x,y)是像素点(x,y)处的对比度值，lij代表应用频散补偿法对第i个驱动器激励、第j个传感器接收的信号进行计算得到的缺陷与传感器j的距离，Lij代表像素点(x,y)与传感器j的距离。为了对比成像结果，将上述方法与常用的延时叠加算法[16]得到的结果比较，延时叠加算法：

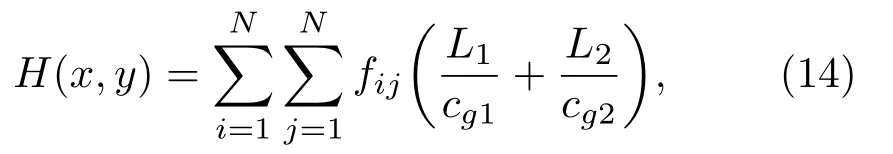
其中，fij(t)代表第i个驱动器激励、第j个传感器接收的散射信号，L1和L2分别代表像素点(x,y)与传感器i、j的距离，cg1为激励的Lamb 波模式的群速度，cg2为缺陷回波中主要传播模式的群速度。

建立如图6所示的三维板有限元模型，板的尺寸为1 m×1 m×0.004 m，模型的材料、激励信号以及激发方式与二维模型建模方法一样，其中中心传感器的坐标为(0.500, 0.500)m，水平方向和竖直方向传感器的间隔均为0.15 m，缺陷为10 mm的半通孔，中心位置坐标为(0.575, 0.425)m。

图6 传感器布置和缺陷位置示意图Fig.6 Diagram of sensor placement and defect location

图7给出了阵元4 激发、其余各个传感器接收的缺陷回波波形。从图中可以看出由于导波的模式转换和频散现象，缺陷回波信号中包含两个波包，并且每个波包的时间宽度变长。应用聚焦接收的方法对数据进行处理，得到缺陷与各个传感器之间的距离如表3所示。更换激发阵元，对各组缺陷回波数据处理得到式(13)中的lij。

表3 传感器与缺陷之间距离Table 3 Distance between sensor and defect

图7 各传感器接收的缺陷回波信号Fig.7 Defect echo signal received by each sensor

利用仿真得到的缺陷回波信号用上面两种方法进行成像，得到的损伤成像结果如图8所示，图8(a)是延时叠加成像结果图，可以大致判断缺陷的区域，取信号峰值点(0.587, 0.418)m作为损伤位置，由于算法本身的限制以及Lamb 波的频散和模式转换现象，使得缺陷周围区域杂波较多，成像结果的精度较差。图8(b)是基于频散补偿的成像结果图，在缺陷位置处能量集中，可以清楚地判断缺陷的位置，其中信号的峰值位置位于(0.591, 0.408)m，而缺陷的准确位置位于(0.575, 0.425)m，产生误差的原因是缺陷具有一定的尺寸，信号经多次反射使得接收信号的持续时间变长，影响了对缺陷位置识别的精度。对比两种成像方法，为了提高延时叠加成像的分辨率，只能通过增加传感器的数量来抑制其他位置波的干扰，增加了检测的计算量与复杂度。而基于频散补偿的成像方法的精度与检测时传感器的数量多少无关，只需要少数的传感器就可得到分辨率较高的图像，更有利于对缺陷做出正确的评估。

图8 缺陷检测成像Fig.8 Defect detection imaging

4 结论

Lamb 波检测在大型板状结构的无损检测中发挥着重要作用，但是导波的频散和多模式特性使得Lamb 波检测的信号变得比较复杂。本文通过理论分析对与缺陷作用后的回波信号进行聚焦接收，聚焦接收可有效抑制缺陷回波信号的频散和模式转换问题，在此基础上提出缺陷定位成像算法。应用有限元仿真软件建立含有缺陷的铝板声学仿真模型，获取缺陷回波数据，结合铝板的频散曲线在一定距离范围内对各个模式的信号进行频散补偿，提取补偿后信号的峰值，将寻找缺陷位置的问题转化为寻找信号的峰值问题。结果表明当信号补偿距离等于缺陷与换能器之间的实际距离时，得到的信号幅值达到最大，并在二维模型板中验证了此方法在缺陷定位中的准确性。进一步根据频散补偿方法计算得到的缺陷与传感器之间的距离，对三维模型板中缺陷进行成像，成像结果与延时叠加成像结果相比，可以在传感器数量较少的情况下准确地显示缺陷的位置，得到分辨率更高的结果，从而更有望应用于实际缺陷检测中。