基于扰动的结合Off-grid目标的层析SAR三维成像方法

杜 邦 仇晓兰 张 柘 雷 斌 丁赤飚

①(中国科学院空间信息处理与应用系统技术重点实验室 北京 100190)

②(中国科学院空天信息创新研究院 北京 100190)

③(中国科学院大学 北京 100049)

④(苏州空天信息研究院 苏州 215123)

1 引言

层析合成孔径雷达(Synthetic Aperture Radar Tomography,TomoSAR)作为干涉合成孔径雷达技术(Synthetic Aperture Radar Interfemetry,InSAR)的扩展，通过获取斜高向上不同位置的观测数据形成斜高向的合成孔径，具有高程向的分辨能力[1,2]。TomoSAR能够解决由于SAR成像几何带来的叠掩问题，实现真正意义上的三维分辨。近年来，随着星载SAR、机载SAR系统技术水平的提升，分辨率、信噪比等指标不断提高，通过星载或机载SAR层析观测，已可实现观测区域高精度三维点云的生成，甚至获得建筑形变等更高维度的信息[3–5]。

TomoSAR在斜高向的分辨，本质上是信号处理领域常见的谱估计问题，近年来已经有许多相关研究成果。受到系统复杂度或观测周期的制约，TomoSAR的基线数目一般是比较有限的，并且基线分布大多是非均匀的，这些问题限制了传统谱估计算法的应用。由于城区人造建筑设施通常具有较强的散射强度，并且在斜高向上的分布往往是稀疏的，因此，压缩感知(Compressive Sensing,CS)方法[6,7]成为TomoSAR第三维重建时经常采用的有效方法，它能够突破瑞利分辨率的限制，有效降低对观测次数的需求。其中，基于L1范数最小化的方法[8–14]具有很高的分辨能力和鲁棒性，已成为Tomo-SAR三维成像的经典方法。

然而，为了应用压缩感知理论，需要对连续的高程向进行离散化处理，同时假定目标正好位于离散化后的网格上。实际上，无论划分多精细的网格，都无法保证目标正好位于所划分的网格上，也即必然存在离网格(Off-grid)的效应，从而引起压缩感知中的基失配(Basis Mismatch)的问题。文献[15]考虑了观测矩阵为傅里叶矩阵的情况，分析了基失配对压缩感知算法恢复信号的影响，结果表明Off-grid目标的能量会泄露到其邻近网格上，导致重构性能的下降。针对这个问题，一种常见的思路是划分足够密集的网格，但这一方面会导致计算复杂度的增加；另一方面，过于密集的网格[16–18]也会使得观测矩阵中包含大量相干性较高的字典集，严重情况下会导致压缩感知算法的失效。

近年来，也有文献[19–21]针对压缩感知理论的缺陷，提出了最小原子范数优化(Atomic Norm Minimization,ANM)方法重构连续域的值，彻底避免了网格效应，这一类方法也被称为无网格压缩感知(Gridless Compressive Sensing,GCS)。然而ANM采用了全新的信号框架，存在运算量大的挑战，目前在TomoSAR实际数据处理中还少有应用。

另一种降低Off-grid对重构性能影响的思路是将目标偏离网格的误差纳入待估计的参数中[22,23]。例如文献[24]和文献[25]将网格偏离误差建模为一个加性扰动。其中文献[24]方法采用贝叶斯压缩感知的框架，同样面临运算量较大，在TomoSAR实际数据处理应用较少的问题。而文献[25]中提出的方法可以与TomoSAR中常采用的L1范数最小化进行结合[24]，文章在单站雷达一维聚焦和SAR二维成像上验证了所提出算法的有效性。然而，TomoSAR三维成像观测矩阵与上述一维和二维成像的理想傅里叶观测矩阵存在较大差别，不能直接应用。

本文首先考虑了在TomoSAR的基失配问题，首先推导了TomoSAR中针对Off-grid目标的1阶扰动模型，并进一步将结合L1范数最小化的求解方法应用到求解Off-grid TomoSAR模型中，最后用仿真数据和实测机载数据对所提方法进行了验证，证明了方法的正确性和有效性。

本文后续内容安排如下：第2节给出了传统的TomoSAR成像模型及求解方法；第3节推导并分析了Off-grid目标对三维成像的影响，给出了适用于Off-grid目标的TomoSAR三维成像模型，以及结合L1最小范数优化的求解方法；第4节进行实验，通过点目标仿真和中国科学院空天信息创新研究院的8通道机载阵列干涉SAR数据验证了所提方法的有效性；第5节进行总结与展望。

2 TomoSAR信号模型

图1给出了TomoSAR三维成像坐标系下距离-斜高平面内的成像几何关系。假设对某个区域有N个相干的观测，相当于在斜高向上形成了等效合成孔径，采用连续信号模型可以表示为

图1 TomoSAR成像几何关系Fig.1 The geometry of TomoSAR imaging

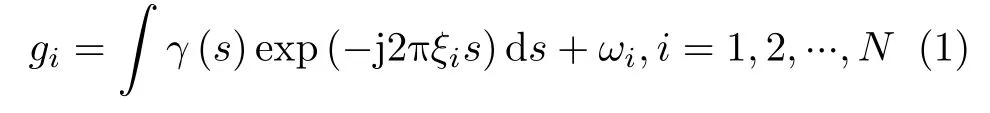
其中，gi表示第i个观测采集到的复数观测值，γ(s)是垂直斜距的高程向(也即斜高向)上散射体的散射系数分布，ξi=2bi/(λr)是 由等效基线bi，雷达波长λ和 斜距r决定的等效空间频率。对上述连续信号模型进行离散化后，表达为矩阵形式如式(2)。

其中，A是N×L大 小的观测矩阵，L为s轴上划分的网格数量，矩阵中第i行 第k列的元素为Aik=exp(-j2πξisk) ,sk是第k个预先划分的网格位置，ε是噪声向量。

在上述模型下，TomoSAR三维成像的目标是通过求解式(2)获得目标的高程s及其后向散射系数γ(s)。L1范数最小化的方法能够较好地处理该问题，其核心思想在于求解以下约束以获得尽可能稀疏的估计。

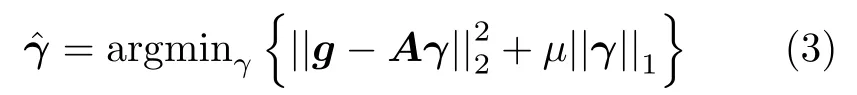
其中，μ是拉格朗日系数[26]，其与观测数量及噪声水平相关。式(3)可以进一步转化为凸优化的问题，利用现有的工具箱如CVX,L1-LS,SPG-L1等进行求解。

3 Off-gird TomoSAR

3.1 一阶差分扰动模型

上述离散网格模型下，如目标恰好均位于离散网格上，则可以得到很好的求解结果，但如果目标不恰好位于网格上，则会存在误差，下面我们分析该误差。传统处理通常将网格均匀划分，网格间距可以用Δs=smax/L进 行表示，其中smax表示斜高向上的最大范围，L代表被划分的网格数。现假设目标与其最近的第k个网格存在偏差 Δk，也即目标的真实位置为sk=(k+Δk)Δs，使用泰勒展开不难得到

其中，o(Δk2)包含了高阶项。整理式(2)和式(4)，本文用组稀疏的形式表示Off-grid目标的TomoSAR模型。

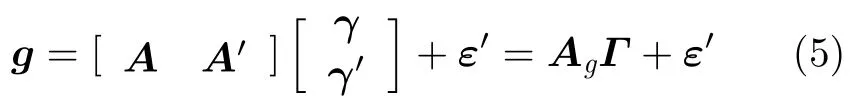
其中，A′可以看成是网格偏差引起的扰动矩阵，矩阵A′和 向量γ′的元素可分别表示为

新的噪声向量ε′中除了原始噪声ε之外，还包含了忽略的高阶展开项。通过求解式(5)，不难进一步通过式(7)求解出k。

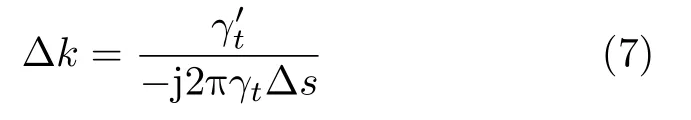
3.2 局部阈值优化

式(5)通过引入扰动项实现了比式(2)更加准确的TomoSAR成像建模，然而，由于网格依然存在，如文献[14]中分析指出，对于Off-grid的目标，求解式(5)恢复的信号与真实信号相比，能量仍会以包络的形式泄露到邻近的网格之上，距离目标真实位置近的网格获得能量多，而距离目标真实位置较远的网格获得能量少。如图2所示，实线表示真实位置上的目标信号，虚线表示恢复出的信号，这会对后续的处理步骤产生影响。为了解决这个问题，本文引入局部阈值优化(Local Optimizing Thresholding,LOT)[27]方法来选择接近真实峰值的网格，判断依据为

图2 高程向目标重建结果的简单示意图Fig.2 Sketch map of the reconstruct results in the elevation direction

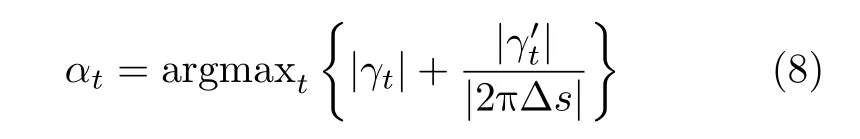
通过式(8)可以得到由αt构成的支撑集。

3.3 算法流程

基于上述模型构建和支撑集确定方法，本文以基追踪降噪(Basis Pursuit De-Nosing,BPDN)进行L1范数最小化求解为例，结合局部阈值优化方法，给出整个算法(Basis Pursuit Local Optimizing Thresholding,BPLOT)的流程，如表1所示。

表1 BPLOT的流程Tab.1 The process of BPLOT

4 实验结果与分析

为了证明本文提出的Off-grid TomoSAR模型和所提求解方法的有效性，下面分别进行点目标仿真实验和实际数据三维成像实验。文中所采用的实际数据为中国科学院空天信息创新研究院机载阵列干涉SAR实验系统获得的山西运城地区的8通道阵列干涉SAR数据[28]。

4.1 点目标仿真

首先本文进行理想点目标仿真实验，仿真参数参考了实测机载阵列干涉SAR飞行实验参数，见表2。在仿真中，本文将斜高向均匀划分为128个网格，同时随机生成目标位置，目标散射系数幅度均归一化为1，相位设置为相互正交，为了方便显示，将高程向s归一化至( 0,1]之间。此处以城市地区常见的叠掩目标稀疏度K=2和K=3的情况为例[29,30]。图3展示了采用本文方法和传统方法的点目标仿真实验结果，蓝色表示真值，红色表示采用L1范数最小化求解式(3)的结果，黄色表示采用本文方法的结果。表3给出了点目标位置的真值以及位置估计结果，其中L1范数最小化方法选取了离真值最近的估计结果(本文后续均采用该评价方法)。由仿真结果可见，采用本文方法得到了更加准确的目标位置估计结果，并且目标的幅度也得到了更好的重建。

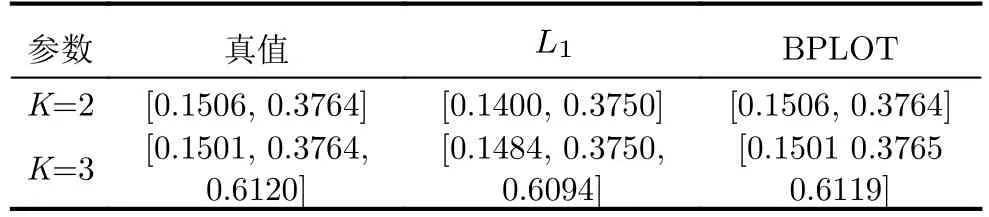
表3 图3对应的位置计算结果Tab.3 Point calculation results corresponding to Fig.3

图3 点目标仿真结果Fig.3 Point target simulation results

表2 仿真参数Tab.2 Simulation parameters

随后，本文通过蒙特卡洛实验评估BPLOT在Off-grid TomoSAR中的统计性能。在每次随机实验中，首先采用估计位置与真实位置的曼哈顿距离来比较本文方法与传统方法对目标位置的估计精度，曼哈顿距离的标准计算公式为

其中，sk表 示第k个散射点的真实位置，表示该散射点的估计位置。当时，本文将该次随机实验作为本文方法优于传统方法的一次抽样，最后通过大量独立重复实验，统计在不同信噪比下本文方法优于传统方法的概率。并且，为了更加严格地进行比较，当K＞1时，本文还分别计算和比较了每个散射点的位置估计精度，统计了本文方法每个散射点位置估计精度均优于传统方法的概率。

本文分别对城市地区常见的稀疏度K=1～3的情况进行了测试，在仿真中添加信噪比为5 dB至20 dB的加性噪声，进行了1000次的独立重复实验，得到的结果如图4和图5所示。图4给出了每个散射点估计位置与真值位置的偏差的统计平均值随信噪比的变化，图中虚线为本文方法结果，实线为传统L1范数最小化的结果，可见在不同稀疏度和不同信噪比下，本文方法对每个散射点都能得到更加准确的位置估计结果。当信噪比大于10 dB时，本文方法对目标位置估计精度能达到0.2个网格间距以内。图5给出了本文方法优于传统方法的概率随信噪比的变化曲线，可以看出：如以总曼哈顿距离来比较，当信噪比为5 dB时，本文方法有约70%的概率优于传统方法；如当每个散射点的估计精度均优于传统方法时才统计为一次更精确的估计，则当信噪比大于13 dB时，本文方法有50%以上的概率能够更精确地估计出每个目标的位置。上述结果验证了本文方法相对于传统On-grid假设L1范数最小化方法的优越性。

图4 散射点位置估计值与真值距离的统计平均值Fig.4 The average distance between the estimated scattering point position and the true value

图5 本文方法优于传统方法的概率与SNR的关系Fig.5 Probability of the proposed algorithm providing better estimation versus SNR

需要说明的是，受到观测数量只有8个的限制，本文方法信噪比较低且稀疏度较大(如K=3)时，估计精度也会受到较大影响。为了考察本文方法在TomoSAR三维成像中的成功概率与观测数量的关系，本文固定SNR=10 dB，在观测数量为8～20的条件下分别进行蒙特卡洛实验，仿真时基线总长度不变，基线间隔随着观测数量的增多而均匀变小。本文将每个散射点DBPLOT＜DOn-gridL1且DBPLOT小于1/8网格间距的随机实验作为一次“成功”且本文方法获得更高精度的概率抽样，从而统计本文方法更精确重建的概率。实验结果如图6所示，可见在信噪比为10 dB时，对于K=2的情况，观测次数为8时本文方法就有50%以上的概率更精确地实现“成功”重建；K=3的情况，观测次数大于11时，本文方法有50%以上的概率更精确地实现“成功”重建。上述仿真结果为本文方法的工程应用提供了参考。

图6 获得更精确估计的概率与观测数量的关系Fig.6 Probability of the proposed algorithm providing better estimation versus number of acquisitions

为进一步评估本方法在重建目标幅度和相位方面的优越性，本文比较了BPLOT和传统L1范数最小化得到的散射系数与仿真设置目标散射系数的均方误差(Root Mean Square Error,RMSE)：

其中，Nt代表了进行独立仿真实验的次数。在该仿真实验中，我们固定观测数量为8，并且只统计本方法每个散射点的位置估计精度均优于传统方法时的散射系数估计结果，从而与图4和图5结果相对应。实验结果如图7所示，方形标记代表K=1，菱形标记代表K=2，叉号标记代表K=3的情况。仿真结果可见，本文方法对于Off-grid目标可以更精确地恢复目标散射系数。

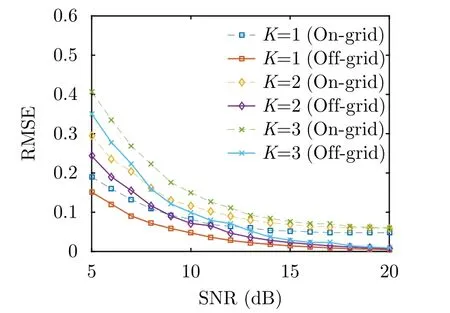
图7 RMSE的计算结果Fig.7 RMSE results

4.2 机载飞行数据

为验证本方法的实用性，本文将其应用于实测机载数据的三维成像处理中。图8(a)给出了整个实验场景的谷歌地球影像，图8(b)为机载SAR获取的该区域的二维图像，场景中的主要目标为人造建筑。

在整个观测场景中，本文选择图8中红框标记的最后一排建筑物的一个局部(图9红框标记所示)作为实验对象，采用本文方法和L1范数最小化方法进行三维成像处理。图10显示了本文方法对所选建筑物的 3-D 点云重建结果，实地考察该楼的高度在53 m左右[31]，重建结果与真值比较接近。为了清晰显示本文方法和传统方法的结果差异，我们截取一个方位向的距离-斜高向切片，如图11、图12所示，蓝色点为直接使用L1范数最小化方法的结果，红色点为采用本文方法的结果。可见，直接采用L1范数最小化时，很难保证目标位于预设网格之上，导致原本只有1个目标的周围会出现错误的多个估计；当采用本文方法后，这些“虚假”目标消失了，并且散射点的位置分布在视觉上更加自然，验证了本文方法的有效性。

图8 从谷歌地球获取的实验地区于2015年的光学影像和对应的SAR图像Fig.8 Optical image of the experiment area obtained from Google Earth in 2015 and SAR image of the corresponding area

图9 图8(a)中最后一排建筑光学影像Fig.9 Optical image of the last row of buildings Fig.8(a)

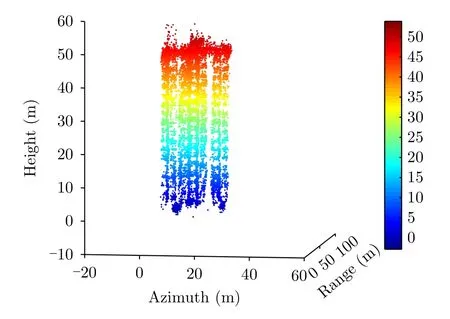
图10 图9中红框建筑的三维重建结果Fig.10 TomoSAR results of the building marked in Fig.9

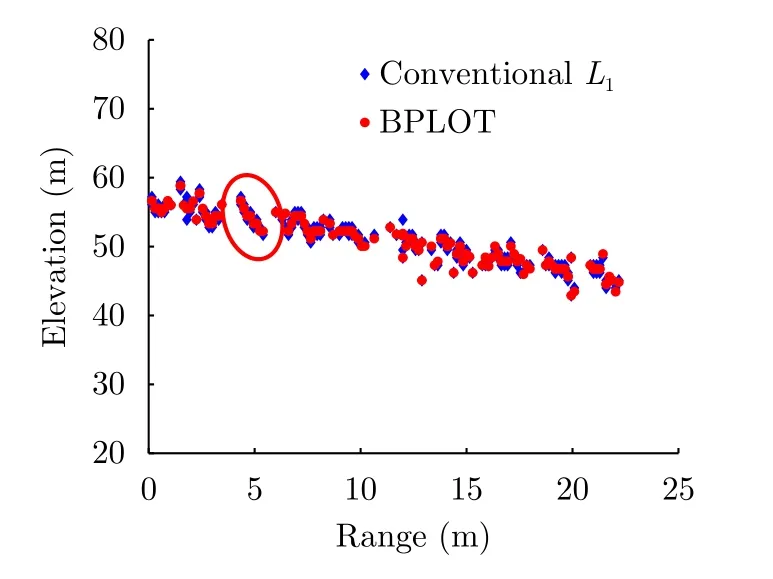
图11 本文方法与传统L1范数最小化的方法对图8中红线标记的方位向切片的成像结果比较Fig.11 Comparison of our method and the conventional process of L1 minimization in the slant range plane for the azimuth-bin marked in Fig.8

图12 图11中区域的放大图Fig.12 Zoom in of the circled area in Fig.11

5 结束语

本文探讨了现有基于压缩感知的TomoSAR处理算法中很少考虑的由Off-grid目标所引起的网格失配问题，提出了基于扰动项的Off-gird TomoSAR成像模型，并采用结合局部阈值的L1最小范数优化方法求解所提出的模型。最后通过点目标仿真，以及在实测机载阵列干涉SAR数据，验证了所提模型的正确性及所提方法的有效性，通过与传统L1范数最小化的处理结果进行对比，证明本文方法能够更精确地估计目标位置，并得到更准确的目标散射系数估计值。