Influence of physical parameters on the collapse of a spherical bubble

Bo-Hua Sun

School of Civil Engineering & Institute of Mechanics and Technology, Xi’an University of Architecture and Technology, Xi’an 710055, China

Keywords:Bubble collapse Rayleigh’s modeling Physical parameters Numerical simulation Maple

ABSTRACT This paper examines the influence of physical parameters on the collapse dynamics of a spherical bubble filled with diatomic gas (κ =7/5). The problem is formulated by the Rayleigh–Plesset dynamical equation, whose numerical solutions are carried out by Maple. Our studies show that each physical parameter affects the bubble collapse dynamics in different degree, which reveals that bubble collapse dynamics must considers all the parameters including liquid viscosity, surface tension, etc, else the outcome cannot be trusted.

In liquid format, bubble cavitation is the formation of vapor cavities when a liquid is subjected to rapid changes of pressure.When subjected to higher pressure, these cavities implode, and generate intense shock waves [1–11]. Although collapsing bubbles generally do not remain spherical, nevertheless, it is often argued that the spherical analysis represents the maximum possible consequences of bubble collapse in terms of the pressure, temperature, noise, or damage potential [2]. Under this understanding, the Rayleigh’s modeling is used in this study, where Rayleigh’s spherical modeling that assumes the bubble remains spherical as shown in Fig. 1.

Fig. 1. Bubble collapse.

Assuming that a bubble in oscillating surroundings is spherical and remains so as it collapses, the bubble radius isR0at timet=0 andR(t), subsequently. With the assumption of polytropic behavior and neglecting of thermal and acoustic dissipation, the Rayleigh–Plesset dynamical equation takes the following form in an oscillating pressure field [5]

the fluid density around the bubble isρ, the fluid surface tension isσ, the fluid viscosity isμ,p∞is the average ambient pressure,pi,eqis internal pressure of bubble,ωis the sound frequency, andηis the dimensionless amplitude of the pressure perturbation which is supposed to be small, in general, the dimensionless pressure amplitudeηis not necessarily small [5].

If the pressure–volume relationship is taken to be adiabatic,then the polytropic exponentκequalsγ, which is the ratio of the specific heats of the gas, henceκ=5/3 for a monatomic gas andκ=7/5 for a diatomic gas.

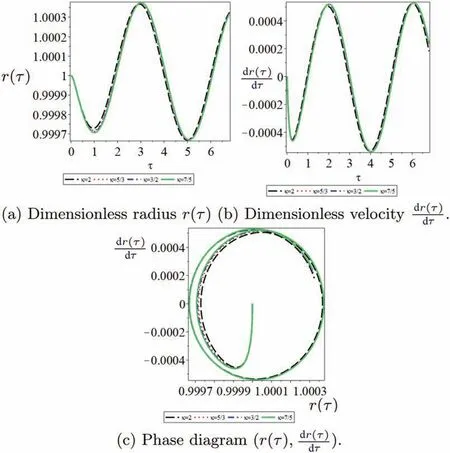
Fig. 2. M=(κ,σ,μ,η,λ,ρ,R0)=(κ =(k+3)/(k+1),σ,μ,η,λ,ρ,R0), k=1,2,3,4.

When both the surface tensorσand liquid viscosityμare neglected. Eq. (1) is still a nonlinear differential equation, merely an analytical solution is obtained for the cases atκ=4/3 [10]. However, if keeping bothσandμ, no analytic solutions have been obtained for bubbles filled with diatomic gas (κ=7/5). The numerical studies that can be found in the literature have shown the extreme richness of Eq. (1) which appears to lie beyond the capabilities of the available analytical techniques [5], therefore numerical method has to be applied [1–11].

If you read the literature [1–11] carefully, it is not difficulty to find that there are no comprehensive numerical solutions for the Eq. (1), and no published computational code as well. Even for some cases do have some curves, however, the curves are plotted in improper scaling which makes the comparison study impossible.In particular, no any dynamics phase diagram of bubble dynamics has even be reported in the literature.

To refine a study of bubble dynamics, this paper revisits the spherical bubble dynamics and writes a general Maple code,which allows all readers can investigate the influence of different physical parameters for their own problems. With our general user-friendly Maple code, we firstly studied bubble dynamics for both monatomic gas (κ=5/3) and diatomic gas (κ=7/5)and their comparisons studies. After that, variational parameter analysis was carried out on different combinations of parameters and their dynamics phase diagram are presented for the first time.

In this paper, after briefly introduce the bubble collapse problems and challenges, we transform the Rayleigh–Plesset dynamics equation into a system of two 1st order differential equations, with our own Maple code different numerical results with discussions are carried. In order to make it easier for readers to reproduce the numerical calculations of this article and to be able to calculate their own problems, a complete Maple code is specially provided in the appendix.

Transformation of bubble dynamics equation and Maple code:

For numerical comparison studies, let us introduce dimensionless variables

Fig. 3. M=(κ,σ,μ,η,λ,ρ,R0)=(κ,σ =0.0725(k −1)/k,μ,η,λ,ρ,R0), k=1,2,3,4.

The full Maple code for solving Eq. (8) under the conditions Eq. (9) is provided in the appendix.

Numerical investigations of Rayleigh collapse dynamics of gas-filled bubble:

In the following numerical results, for simplicity, we introduce a physical parameter vector

(1) Rayleigh collapse dynamics of gas-filled bubble with parameters:M=(κ,σ,μ,η,λ,ρ,R0)=(κ=(k+3)/(k+1),σ,μ,η,λ,ρ,R0), k=1,2,3,4.To observe the effect of the polytropic exponentκon the bubble dynamics, here we only change the exponentκ. The results in Fig. 2 indicate that the polytropic exponent,κ, has small influence on the bubble collapse.

Fig. 4. M=(κ,σ,μ,η,λ,ρ,R0)=(κ,σ,μ=0.001(k −1)/k,η,λ,ρ,R0), k=1,2,3,4.

(2) Rayleigh collapse dynamics of gas-filled bubble with parameters:M=(κ,σ,μ,η,λ,ρ,R0)=(κ,σ=0.0725(k−1)/k,μ,η,λ,ρ,R0), k=1,2,3,4.To observe the effect of the surface tensionσon the bubble dynamics, here we only change the surface tensionσ.The results Fig. 3 confirm that the surface tension,σ, also has small influence on the bubble collapse ifσ/=0, while change dramatically if the surface tensionσ=0,the reason behind this huge change is that there is no resistance in the absence of surface tension.It must noted that the different values of liquid surface tensionσare used here are not real and only for parametrical study, since water surface tension isσ=0.0725 kg/s. This also applies to other parameters.

(3) Rayleigh collapse dynamics of gas-filled bubble with parameters:M=(κ,σ,μ,η,λ,ρ,R0)=(κ,σ,μ=0.001(k−1)/k,η,λ,ρ,R0), k=1,2,3,4 To observe the effect of the liquid viscosityμon the bubble dynamics, here we only change the liquid viscosityμ.The results in Fig. 4 show that the liquid viscosity,μ, has an obvious influence on the bubble collapse. In particular,the bubble collapse forμ=0 is dramatically different. The physics behind this phenomena is that zero viscosity offers little damping, which is unrealistic since a liquid always has a certain viscosity. This study reveals that bubble collapse dynamics must considers liquid viscosity, else the outcome cannot be trusted.Particularly noteworthy, as the viscosityμincrease, because the bubble dynamics is damped by viscosity, the bubble dynamics loses energy. As the amplitudes of the velocity and radius decrease, the phase trajectory spirals inwards as shown in the phase diagram of Fig. 4. In classical mechanics, this is described as an “attractor” and shows that the system is trapped in a potential well from which it cannot escape. Other cases in this paper have similar situation.

(4) Rayleigh collapse dynamics of gas-filled bubble with parameters:M=(κ,σ,μ,η,λ,ρ,R0)=(κ,σ,μ,η=0.02(k−1),λ,ρ,R0), k=1,2,3,4.To observe the effect of the oscillation amplitude parameterηon the bubble dynamics, here we only change the oscillation amplitude parameterη. The results in Fig. 5 show that the oscillation amplitude,η, of the surrounding liquid has a strong impact on the bubble collapse dynamics.

(5) Rayleigh collapse dynamics of gas-filled bubble with parameters:M=(κ,σ,μ,η,λ,ρ,R0)=(κ,σ,μ,η,λ=ωk/ω0,ρ,R0), k=1,2,3,4.To observe the effect of the oscillation frequencyωon the bubble dynamics, here we only change the oscillation frequencyω. The results in Fig. 6 reveal that the oscillation frequency,ω, of the surrounding liquid also has a strong impact on the bubble collapse dynamics’magnitude. Together with the amplitude influence, it is concluded that the bubble collapse is sensitive to any change in the surrounding liquid environment.

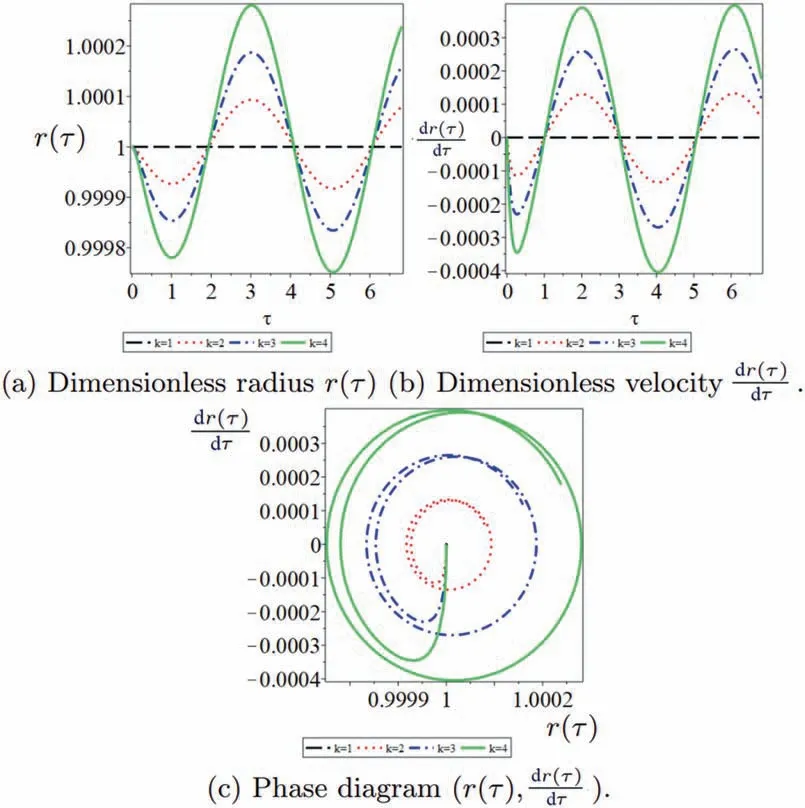
Fig. 5. M=(κ,σ,μ,η,λ,ρ,R0)=(κ,σ,μ,η =0.02(k −1),λ,ρ,R0), k=1,2,3,4.

(6) Rayleigh collapse dynamics of gas-filled bubble with parameters:M=(κ,σ,μ,η,λ,ρ,R0)=(κ,σ,μ,η,λ,ρ=ρ0(k+1)/k,R0), k=1,2,3,4.To observe the effect of the fluid densityρon the bubble dynamics, here we only change the fluid densityρ.The results in Fig. 7 demonstrate that the fluid densityρhas a moderate degree of impact on the bubble dynamics.

(7) Rayleigh collapse dynamics of gas-filled bubble with parameters:M=(κ,σ,μ,η,λ,ρ,R0)=(κ,σ,μ,η,λ,ω0,ρ,R0=0.001k), k=1,2,3,4.To observe the effect of the initial radiusR0on the bubble dynamics, here we only change the initial radiusR0. The results in Fig. 8 show that the initial radius,R0, has a strong influence on the bubble dynamics as the smaller theR0, the less energy in the bubble.

(8) Rayleigh collapse dynamics of gas-filled bubble with parameters:M=(κ,σ,μ,η,λ,ρ,R0)=(κ,σ=0.001(k−1)/k,μ=0.0725(k−1)/k,η,λ,ω0,ρ,R0), k=1,2,3,4.

To observe the combined effect of the surface tensionσand fluid viscosityμon the bubble dynamics, here we change both of them simultaneously. The results in Fig. 9 clearly show that the bubble radius has strong impact on bubble dynamics.

The results in Fig. 10 clearly show that the bubble radius, without surface tension and viscosity, is much larger when gases are included, which means that the surface tension and viscosity play a important role to inhibit bubble dynamics processes. In particular, in the absence of an extreme case of the surface tension and viscosity, the bubble dynamic is very intense.

In conclusion, the comprehensive numerical investigations show that bubble collapse dynamics are influenced by the combined effects of surrounding liquid environment, surface tension,viscosity, as well as the initial bubble radius. However, each parameter affects the bubble collapse dynamics in different degree.No parameters should be omitted on studying bubble dynamics investigation.

Fig. 6. M=(κ,σ,μ,η,λ,ρ,R0)=(κ,σ,μ,η,λ=ωk/ω0,ρ,R0), k=1,2,3,4.

Fig. 7. M=(κ,σ,μ,η,λ,ρ,R0)=(κ,σ,μ,η,λ,ρ =ρ0(k+1)/k,R0), k=1,2,3,4.

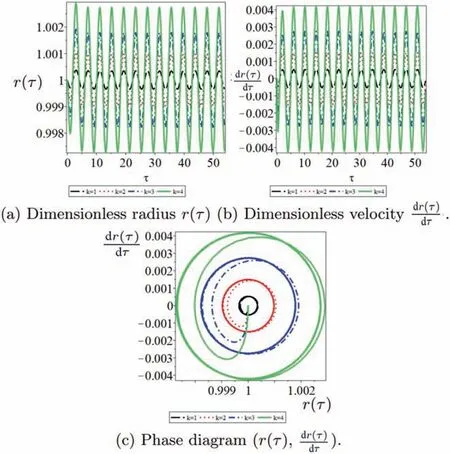
Fig. 8. M=(κ,σ,μ,η,λ,ρ,R0)=(κ,σ,μ,η,λ,ρ,R0 =0.001k), k=1,2,3,4.

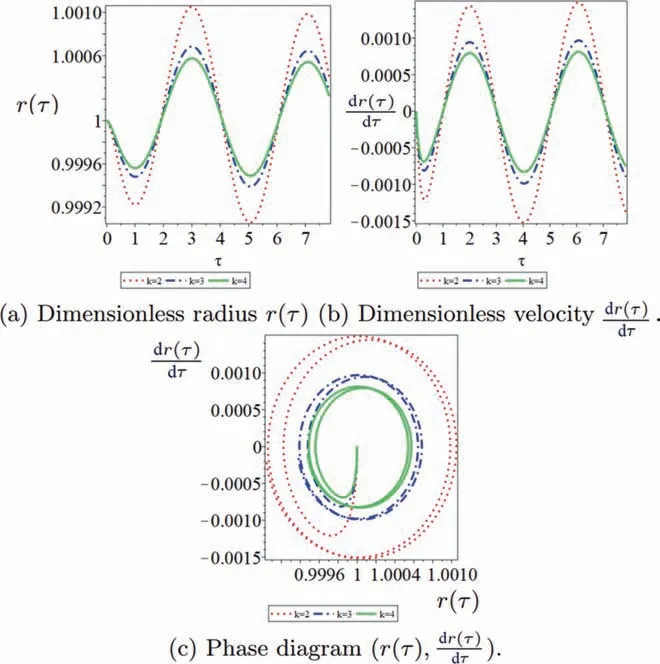
Fig. 9. M=(κ,σ,μ,η,λ,ρ,R0)=(κ,σ =0.001(k −1)/k,μ=0.0725(k −1)/k,η,λ,ρ,R0), k=2,3,4.

Fig. 10. M=(κ,σ,μ,η,λ,ρ,R0)=(κ,σ =0.001(k −1)/k,μ=0.0725(k −1)/k,η,λ,ρ,R0), k=1,2,3,4.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Maple code of bubble dynamics

with(student); with(DEtools); with(plots); restart; for k from 0 to 4 do kappa := (k + 3)/(k + 1); mu := 0.001; sigma :=0.0725; rho := 0.001; R0 := 0.001; p1 := 1.00000*1.01971621;p0 := 2*sigma/R0 + p1; omega0 := sqrt(p0/(rho*R0∧2)); omega:= 1.54*omega0; eta := 0.8; alpha := sigma/(R0*p0); beta :=mu/(R0*sqrt(rho*p0)); delta := p1/p0; lambda := omega/omega0;Q := r(tau)∧(-3*kappa) - 2*alpha/r(tau) - 4*beta*y(tau)/r(tau)- delta*(1 + eta*cos(lambda*tau)); eq1 := diff(r(tau), tau) =y(tau); eq2 := r(tau)*diff(y(tau), tau) + 3/2*y(tau)∧2 = Q; sol:= dsolve([eq1, eq2, r(0) = 1, y(0) = 0], numeric, output =listprocedure); rr[k] := rhs(sol[2]); dr[k] := rhs(sol[3]); print(k);end do;

Plotting dimensionless radiusr(τ)command is: with(plots):plot([seq(rr[k](tau), k = 0 ... 4)], tau = 0 ... 2.6*10∧6/omega 0, legend = [”k=0”, ”k=1”, ”k=2”, ”k=3”, ”k=4”], linestyle = [3, 2, 4, 1,5], color = [”black”, ”red”, ”blue”, ”green”, ”brown”], thickness = 3,axes = boxed).