基于遗传算法的复合材料进气道铺层角度优化及分析验证

赵博伟，赖 辉

（成都飞机工业（集团）有限责任公司 技术中心，四川 成都 610092）

复合材料由于具有高的比强度、比模量及可设计性等优点，在航空领域得到广泛应用，使结构承载能力得到保证的同时减轻结构重量。近年来，复合材料在飞机结构中的使用量逐步提高，从一般构件、次承力构件到主承力构件都有复合材料替代金属材料的实例。

提高结构承载能力，是飞机结构设计的重要目标之一。结合复合材料的可设计性，可对复合材料铺层进行优化，使之在结构重量不变的前提下，提高结构承载能力。

通过几十年的技术发展，复合材料优化方法有了很大的进步。目前常用的优化方法包括遗传算法[1]、神经网络法[2]、图表法优化[3]及其他基于各自不同的设计目标和约束所形成的工程处理方法。

本文采用HYPERWORKS软件为平台，采用遗传优化算法对某型飞机的S型复合材料进气道，以提高承载能力为目标对复合材料铺层角度进行优化设计，提供工程中可靠的优化方法及在HYPERWORKS中的具体表现方式。这种优化方法在工程中已得到充分应用，并对承载能力通过了有限元分析及试验验证，得到了满意的结果。

1 优化模型概述

结构应变能是决定结构承载能力的重要指标之一，对于复合材料进气道结构，在既定载荷及边界条件的情况中，结构承载能力越强，其相应的应变及位移就越小，外力做功及结构应变能也就越小。在不考虑体力的情况下，结构应变能的有限元形式如下所示：

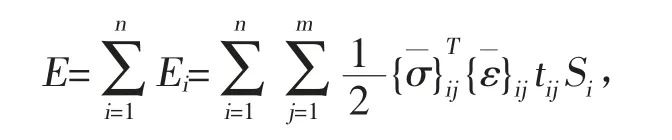
式中：{σ}ij是第i个单元第j层的应力；{ε}ij是第i个单元第j层的应变；Si是第i个单元的面积；tij是第i个单元第j层的厚度；n是结构的单元数；m是第i个单元的层数。其中：

[K]ij为第i个单元第j层刚度矩阵，对复合材料：

式中：c=cosθj，s=sinθj。

铺设角优化模型如下。

1.1 目标函数

优化铺设角过程，就是以进气道整体结构的应变能最小为目标：

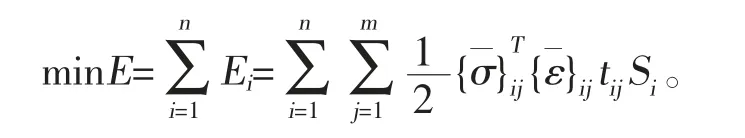
1.2 设计变量

复合材料进气道铺层共有12层，由于进气道采取对称铺层，所以只需优化一半铺层角度，因此设计变量为6个铺层角度，根据工程实际情况，各铺层的铺设角是在规定范围内选取的，因此要对铺设角设定上限θm及下限θl：

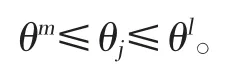
1.3 约束条件

约束条件包括强度约束、刚度约束，以及损伤容限约束。这里采用Tsai-Hill失效准则；

强度约束保证进气道复合材料均满足失效判据，即F.I＜1；刚度约束为进气道的位移约束△i＜[△i]；根据损伤容限设计原则，复合材料表面采用建议铺层角度。

优化过程采取遗传算法。Bagley[4]于1967年首次提出遗传算法（Genetic Algorithm）的概念，之后，该算法成为求解系统优化问题的框架，逐渐成熟并被广泛应用于多个学科领域，它具有不依赖于问题的具体领域和鲁棒性强的优点。优化通过调用HYPERWORKS软件进行分析，并对HYPERWORKS的输入初始铺层文件和输出分析数据文件进行读写操作。通过分析数据文件中读取的结果数据进行分析，通过优化程序改写初始铺层文件进行迭代优化，具体流程如图1所示。

图1 遗传算法优化流程

1.4 收敛准则

当两次迭代循环的结构k区域的应变能之差绝对值小于给定值或迭代次数达到给定值时，终止迭代。

2 计算及优化结果

进气道采用二维层合壳单元，赋予PCOMP单元属性，筋条表面材料采用二维层合板壳单元，筋条内部填充物为泡沫材料，采用三维实体（C3D8）单元。唇口均采用二维单元，进气道上的网格总数为36 846个，进气道剖面及有限元模型如图2所示。

图2 进气道结构

从进气道初始铺层角度设计为“[45°/-45°/0°/55°/-55°/0°]s”，边界条件设置为进气道两端固支，取吸力载荷-22 444 Pa进行有限元分析，安全系数为1.3。

从进气道静力计算结果可以看出，进气道最大应力值发生在进气道端口上端，此处曲率较大。最大应力为153.5 MPa，如图3（a）所示；最大变形发生在右进气道左边，靠近端口部位。最大变形值为1.851 mm，如图3（b）所示。

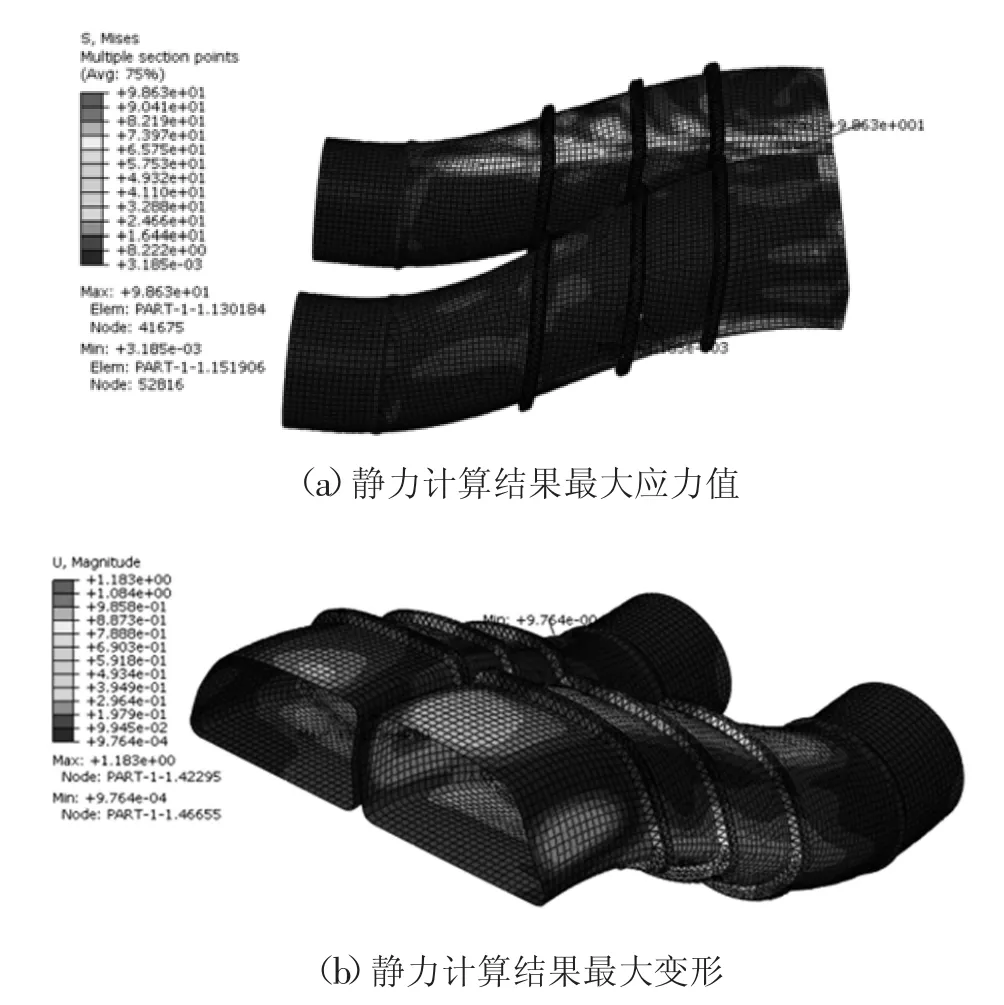
图3 静力计算结果最大应力值及最大变形

在初始铺层优化模型及力学分析的基础上，对结构的铺层进行优化。保持进气道的总厚度不变，共12层，单层厚度为0.125 mm。根据实际要求，铺设角度范围为-65°～65°。刚度约束中的位移约束[Δi]=1.8 mm，同时根据损伤容限要求，复合材料表面采用±45°铺层。

通过优化模型，计算得到的优化铺层角度为“[45°/-45°/0°/65°/-65°/0°]s”。对优化后的进气道进行静力计算，工况与上同，得到应力云图如图4（a）所示，最大应力为148.6 MPa，对比初始铺层减小3.2%；位移云图如图4（b）所示，最大位移为1.827 mm，对比初始铺层减小1.3%。

图4 铺层优化后最大应力值及最大变形

试验方案及试验现场如图5所示。在吸力载荷-22 444 Pa下，各测点位移模拟值和试验值对比如图6（a）所示，应变测点1上0°应变对比如图6（b）所示。试验结果与理论计算结果吻合情况良好，工况卸载后，进气道能恢复初始状态，未出现有害变形、损伤、裂纹及破坏。

图5 试验方案及现场

图6 模拟值和试验值对比

3 结论

（1）本文描述的优化模型是建立在有限元分析软件HYPERWORKS的基础上，有限元模型及分析由HYPERWORKS完成，软件用特定的优化方法操作输入文件，且不影响模型完整性，该优化过程具有较高的实用性及通用性。

（2）各区域应变能减少，说明文中铺层优化方法有效，在铺层总厚度及单层厚度不变的情况下，提高了结构承载能力。

（3）本文采用遗传算法，迭代次数较少，优化效率较高。

（4）该优化过程可以灵活应用，不仅可以以应变能最小为目标优化，也可以以结构刚度最大为目标进行优化。