火灾下四种不同边界双向板的极限承载力计算
2022-03-04朱三凡董毓利张大山段进涛
朱三凡,董毓利,张大山,段进涛
(1. 华侨大学土木工程学院,福建,厦门 361021;2. 健研检测集团有限公司,福建,厦门 361004)
钢筋混凝土板在火灾下发生大挠度时的承载力比塑性铰线理论计算值大得多,这是因为在混凝土板内产生了受拉薄膜效应[1-8]。目前,国内外学者根据各自提出的薄膜效应产生机理,推导出了一些计算方法,但存在计算过程比较复杂、假设条件太多等问题[9-15]。作者所在的课题组也在这方面进行了深入研究:董毓利[16]用变形和分解原理求解了混凝土板的受拉薄膜效应,给出了没有水平约束的矩形、方形双向板极限承载力计算公式,杨志年[17]、朱崇绩等[18-19]、张大山等[20-21]在此基础上提出了考虑受拉薄膜效应的火灾下钢筋混凝土四边简支双向板、四边固支双向板、邻边简支、邻边固支双向板、仅在柱上有梁的双向板楼盖和平板无梁楼盖单向板的极限承载力计算公式。
本文在课题组原有工作的基础上,对三边简支一边固支、三边固支一边简支、两长边固支两短边简支、两长边简支两短边固支四种不同边界钢筋混凝土双向板极限承载力计算作进一步研究。
1 塑性铰线理论
基本假定[17-18,21]:适筋板的破坏起始于受拉钢筋的屈服。发生破坏时,在塑性铰线处发生塑性变形及受拉钢筋屈服。钢筋未出现硬化。
基于经典塑性铰线理论,火灾下三边简支一边固支、三边固支一边简支、两长边固支两短边简支、两长边简支两短边固支四种不同边界双向板的破坏模式见图1~图4。

图1 三边简支一边固支双向板的塑性铰线模式Fig. 1 Plastic hinge line configuration of the slab with simply supported on three sides and clamped on one side

图2 三边固支一边简支双向板的塑性铰线模式Fig. 2 Plastic hinge line configuration of the slab with simply supported on one side and clamped on three sides

图3 两长边固支两短边简支双向板的塑性铰线模式Fig. 3 Plastic hinge line configuration of the slab with simply supported on two long sides and clamped on two short sides

图4 两长边简支两短边固支双向板的塑性铰线模式Fig. 4 Plastic hinge line configuration of the slab with simply supported on two long sides and clamped on two long sides
在双向板中心位移达到v时,钢筋合力方向不再保持水平,而是与水平向形成了一个角度θ,产生了竖向分力Tsinθ,如图5 和图6 所示。随着板中竖向位移的继续增大、板底钢筋温度的持续升高,混凝土压力C和钢筋的合力T均不断减小,钢筋竖向分力Tsinθ不断增大,薄膜效应不断增强板的极限承载力也相应提高[16]。,

图5 塑性铰线截面的受力Fig. 5 Forces at the yield hinge section of the slab

图6 竖向位移及转动角示意图Fig. 6 Diagram of vertical displacement and rotation angle
2 基于塑性铰线理论的承载力计算
2.1 板块平衡法
以三长边固支一短边简支双向板为例,常温下:
板块①绕AD轴转动的平衡方程为:

板块②绕AB轴转动的平衡方程为:

板块③绕BC轴转动的平衡方程为:

板块④绕CD轴转动的平衡方程为:

式(1)~式(4)中:mx、my分别为常温下塑性铰线处x、y两个方向的截面抵抗矩;mxe、mye分别为x、y两个方向固支边轴线处的负弯矩;q为混凝土板的承载力,包括板的恒载及板面活荷载。
由板块几何关系可知:y1=y2=l/2
由式(1)~式(4)可以解得:

混凝土板形成塑性铰线后,塑性铰线的位置就已确定,并且随着挠度的增大,位置不再发生变化,故常温下计算得到的xi、yi可用于高温下双向板极限承载力计算。
高温下,受拉钢筋竖向分力参与受力,板内产生薄膜效应后,式(1)~式(4)应变化为:


其中:


三边固支一边简支双向板的极限承载力为:

基于板块平衡法同样可以对三边简支一边固支、两长边固支两短边简支及两长边简支两短边固支三种边界的双向板进行求解。
三边简支一边固支双向板:

两长边固支两短边简支双向板:

两长边简支两短边固支:


将本文所提出的四种边界双向板求得的极限承载能力计算公式与文献[17 - 18]所提出四边简支、四边固支、邻边简支邻边固支三种边界双向板极限承载力计算公式进行汇总,汇总结果见表1。其中,式(23)~式(26)为四边简支双向板各板块极限承载力计算公式。由表1 及板块平衡方程式(1)~式(4)可知,基于板块平衡法双向板各板块的极限承载力计算公式仅与各自板块的边界条件有关,与其他板块的边界条件无关;不同边界条件双向板中相同边界条件的板块极限承载力计算公式相同,但塑性铰线位置xi、yi不同。


表1 火灾下不同边界双向板极限承载力(板块平衡法)Table 1 Load-carrying capacity of two-way slabs with different boundary (plate balance method)

在表1 基础上整理得到可适用于各种边界条件的双向板极限承载力计算通用公式:

式中:k=0,1为所属板块有固支边时为1,无固支边时为0;i=1,2为q1和q3计算时,i分别取为2 和1,q2和q4计算时,i分别取为1 和2。
2.2 能量法
以两长边固支两短边简支双向板为例,大挠度情况下,板的张拉薄膜效应在塑性铰线出现后产生,且产生薄膜效应的原因是塑性铰线截面处屈服钢筋伸长所做塑性功[16]。塑性铰线BE绕AB、BC转动时钢筋伸长所做功为:

塑性铰线AE绕AB、AD转动钢筋伸长所做功为:


塑性铰线CF绕CD、BC转动钢筋伸长所做功为:

塑性铰线DF绕轴线CD、AD转动时钢筋伸长所做功为:

塑性铰线EF绕AB、CD轴转动时钢筋伸长所做功为:
上述法律人士同时表示,在司法实践中,罚金刑经常会遇到执行难问题,为了解决这一问题,有不少法院会以从轻处罚作为交换条件,促使被告人在正式宣判之前先缴纳罚金,从而解决“判了白判”的问题。所以,开庭前催罚金也就成了不少法院(尤其是基层法院)的普遍做法。

截面弯矩转动做功为:

钢筋伸长所做的功为:

外力做功与内力做功相等,W=D1+D2,由式(39)~式(41)可以得到两长边固支两短边简支双向板的极限承载力:


将本文所提出的基于塑性铰线理论能量法的四种边界双向板极限承载力计算公式与文献[17 - 18]所提出三种边界双向板极限承载力计算公式进行汇总,汇总结果见表2。式(47)为四边简支双向板极限承载力计算公式。从表2 可知,基于塑性铰线理论能量法计算不同边界双向板承载力极限计算公式与所有板块的边界条件均相关,各种边界条件下承载力均可在四边简支板计算公式的基础上加上固支边弯矩产生的承载力分量得到。

在表2 基础上整理得到可适用于各种边界条件双向板极限承载力计算通用公式为:

表2 火灾下不同边界双向板极限承载力(能量法)Table 2 Load-carrying capacity of two-way slabs with different boundary (energy method)

式中,k=0,1——所属板块有固支边时为1、无固支边时为0。
3 试验验证
为了验证以上双向板承载力计算公式,本课题组进行了四种边界条件类型的足尺钢筋混凝土双向板的火灾性能试验[23-24],每种边界条件均有两个试件(本文各选取一个试件进行验证),表3为各试件主要参数表,各板的外加荷载均为5.0 kN/m2(含自重3.0 kN/m2)。

表3 试件的主要参数Table 3 Main parameters of specimens
选取双向板中心竖向位移和底层钢筋温度的试验结果,根据表1 中计算公式可以得到各试件承载力。图7 和图8 分别为基于板块平衡法和基于能量法的ES1~ES3 试件火灾作用下承载力计算值与底层钢筋温度变化关系曲线(图中传统方法为不考虑薄膜效应的塑性铰线理论公式),表4 为各板在火灾下双向板极限承载力结果对比。

表4 火灾下双向板极限承载力结果对比Table 4 Comparison of ultimate bearing capacity of two-way slabs under fire
从图7 和图8 可以看出:传统计算方法与本文计算方法,在下层钢筋温度超过400 ℃时,板的极限承载力出现快速下降,这是因为钢筋的屈服强度在高于400 ℃的温度下会出现大幅度的折减[22]。根据本文公式计算的极限承载力值,在板中挠度小于v0时,承载力为常值;在板中挠度大于v0后,板的承载力开始变大,这是因为板的薄膜效应开始显现。

图7 承载力随温度的变化(板块平衡法)Fig. 7 Curve of bearing capacity with temperature(plate balance method)

图8 承载力随温度的变化(能量法)Fig. 8 Curve of bearing capacity with temperature(energy method)
根据基于传统板块平衡法计算,试件ES1~ES3在底层钢筋温度为603 ℃、650 ℃、628 ℃时出现破坏,即极限承载力小于5.00 kN/m2,而此钢筋温度对应各板中心竖向位移分别为l/24、l/23、l/27,均尚未达到l/20[25-26]的双向板破坏准则,板仍具有一定的抗火能力。可见传统计算方法因为未考虑高温下双向板薄膜效应对承载力的提高作用,而导致计算结果偏于保守。根据本文提出计算公式,试件在关火时的极限承载力分别为5.31 kN/m2、5.00 kN/m2和5.27 kN/m2,相对应的板中心竖向位移分别为l/22、l/20、l/25,与试验结果基本吻合。
根据基于传统能量法计算,试件ES1~ES3 在底层钢筋温度为656 ℃、690 ℃、680 ℃时出现破坏,而此钢筋温度对应各板中心竖向位移分别为l/22、l/22、l/25 ,同样未达到l/20的破坏准则,可见传统计算能量法与传统板块平衡法存在的问题,计算结果仍偏于保守,但偏离程度低于板块平衡法。根据本文提出计算公式,试件在关火时的极限承载力分别为5.40 kN/m2、5.09 kN/m2和5.35 kN/m2,比本文提出的板块平衡法计算值略大,存在2%左右的偏差,与试验结果基本吻合。
图9 是板中竖向位移分别为l/15、l/20、l/25、l/30时,通过式(27)、式(28)得出的ES1~ES3 板承载力计算结果对比(ES1~ES3 板底钢筋温度取试验结果,板块平衡法)。从图9(b)可以看出停火时,竖向位移为l/20板承载力计算结果为5.00 kN/m2,与试验结果吻合;竖向位移为l/15、l/25、l/30时的计算结果与试验均存在不同程度的偏差;验证了选取l/20作为破坏准则的正确性。从图9(a)和图9(c)可以看出,在停火时,ES1 和ES3 板在给定竖向位移为l/20~l/30之间时承载力计算结果接近5.00 kN/m2,与竖向位移l/20的破坏准则存在一定偏差。分析产生偏差的原因是,与ES2 板相比,ES1 和ES3 板板底钢筋温度低了很多,而钢筋的屈服强度随温度升高将出现大幅度的降低。

图9 板的极限承载力随竖向位移变化Fig. 9 Ultimate bearing capacity of slab varies with vertical displacement
需要指出的是,在根据式(21)对两长边简支两短边固支双向板ES4 进行计算时发现:x1>L/2,即该双向板的塑性铰线模式与图4 不符合,故本文不对其进行验证。根据ES4 板的轴线尺寸、配筋及边界条件进行测算,只有在L/l>1.74的情况下,该板的塑性铰线模式才会与图4 相符合,表1中的计算公式才适用。在L/l≤1.74的情况下,可按方形板进行计算。
此外,利用表1 和表2 中公式进行双向板承载力计算时,板底钢筋温度将对最终计算结果产生较大的影响。图10 为ES1 板中热电偶布置图,图11 为ES1 板中部T3~T6 等4 个板底钢筋温度测点的实测钢筋温度-时间曲线。从图中可以看出,尽管处于同一火场内,但不同位置处板底钢筋温度仍存在较大的差异:受火210 min 时,T3~T5 测点钢筋温度分别为664.0 ℃、626.4 ℃、658.4 ℃、823.2 ℃,最大温差达196.8 ℃;与此相对应的钢筋屈服强度折减系数分别为0.316、0.407、0.330、0.098,差异很大。在表4 的双向板极限承载力计算中,本文根据各参数所代表的物理意义及其所处位置的不同,选取不同测点板底钢筋实测值作为其计算过程中对应的温度。图12 为板底钢筋温度测点布置与塑性铰线破坏模式关系,表5 为双向板极限承载力计算值各参数温度取值表。

表5 双向板极限承载力计算时各参数温度取值Table 5 Temperature value of each parameter in the calculation of ultimate bearing capacity of two-way slab

图10 热电偶布置图 /mmFig. 10 Arrangement of thermal couples
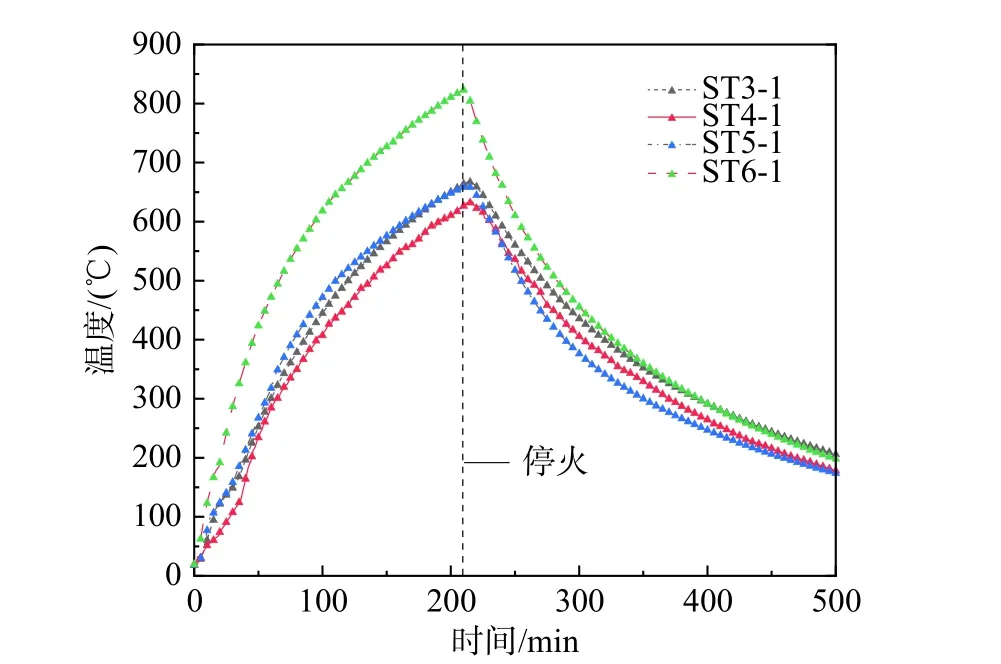
图11 板底钢筋温度-时间曲线Fig. 11 Temperature time curve of bottom reinforcement

图12 板底钢筋温度测点布置与塑性铰线破坏模式 /mmFig. 12 Arrangement of temperature measuring points and plastic hinge line configuration of the slab
4 结论
本文通过对三边简支一边固支、三边固支一边简支、两长边固支两短边简支、两长边简支两长边固支四种不同边界钢筋混凝土双向板极限承载力计算进行研究,主要得出以下结论:
(1) 本文基于塑性铰线的板块平衡法与能量法给出了四种不同边界双向板极限承载力计算公式,计算结果与试验结果较吻合,传统塑性铰线理论公式因未考虑薄膜效应,计算结果偏保守。
(2) 在整合其他边界双向板计算公式的基础上,提出了火灾下基于塑性铰线理论板块平衡法和能量法各种边界双向板极限承载力计算的通用公式。
(3) 火灾下矩形双向板的塑性铰线理论破坏模式存在与传统塑性铰线理论破坏模式不一致的可能性,在使用本文提出计算公式前需先进行确认。
