麻城黄山松天然林直径分布
2022-03-04侯梅胡剑民张琴琴汪洋
侯梅, 胡剑民, 张琴琴,, 汪洋,
麻城黄山松天然林直径分布
侯梅1, 胡剑民2, 张琴琴1,*, 汪洋1,*
1. 湖北生态工程职业技术学院,武汉 430200 2. 麻城市职业技术教育集团, 湖北麻城 438300
为研究黄山松天然次生林直径分布特征, 以麻城市黄山松天然次生林为研究对象, 采用标准样地调查, 计算林分直径的偏度、峰度, 林分直径分布的Shannon-Weiner和Simpson指数, 运用负指数分布、normal分布、lognormal分布、logistic分布和Weibull分布等5种概率密度函数对黄山松天然次生林林分直径分布进行拟合, 对拟合结果进行2检验。结果表明: 1)黄山松直径分布主要为左偏山状, 较高径阶林分直径分布为右偏山状。2)黄山松直径分布的多样性和均匀度指数与林分径阶的大小变化一致。3) Weibull分布函数拟合接受率为75.0%, 适宜解释黄山松天然林林木直径分布。研究结果可为黄山松天然林分直径分布和生长动态提供参考依据, 指导黄山松天然林的经营与管理。
黄山松; 天然次生林; 直径分布; Weibull分布
0 前言
黄山松()为中国特有树种, 是中国亚热带中部海拔800—1800 m低山或中山森林的主要建群种[1]。在湖北东部、河南南部大别山区海拔700—1600 m的山地, 大部分黄山松天然次生林因封山育林径级增大, 逐步演变为以黄山松为优势种的纯林。长期以来, 由于黄山松自身生物学特性、密度效应与环境适应策略, 导致种群优势地位持续增强[2], 导致出现黄山松天然次生林群落层次简单、乔木层树种单一、生物多样性较低和生态系统稳定性弱等问题, 黄山松天然林应有的生态功能难以发挥[3]。
林分结构的特性是决定森林能否充分发挥其功能的前提[4], 林木大小分布规律是林分结构的基本属性, 与森林生物量、碳储量和总生产量等特征密切相关[5-6]。林分直径分布反映了林分群落结构和生长规律, 能够反映出森林动态和过去所受干扰的持续影响, 适宜的直径分布模式是诊断森林结构是否稳定的一个重要指标, 也是林分独特生长模式的结果[7], 因而是最重要和最基本的林分结构[8], 历来受到国内外学者的关注[9]。
直径分布模型选择可以指导调节林分直径结构, 使林分植株在中小径级时获得足够资源, 促使小径级林木的正常生长和林下更新[10], 从而提高生物多样性、提高生态服务功能和群落保护。近年来, 直径分布研究中应用较多的主有要Weibull分布、Logistic分布、负指数分布、正态分布以及对数正态分布等[7, 11-13]。由于森林类型、分布区域和立地条件的差异, 相应林分直径分布模型可能不同[11], 有针对性地研究具有代表性的林木直径分布模型十分重要。
本文以湖北省麻城市三河口镇狮子峰林场隘门关村不同林龄的黄山松天然次生林为对象, 研究黄山松天然次生林林分直径分布规律。在充分了解黄山松林分不同发育阶段直径结构特性的基础上, 确定黄山松林分发展阶段, 为造林设计[14-15]、建立林分生长和收获模型[16-17]提供依据, 促进黄山松群落健康发展, 维护生物多样性和生态系统稳定性。
1 研究地概况
研究地位于湖北省东北部麻城市三河口镇狮子峰林场隘门关村。地理坐标为115°17'23"—115°21'41"E, 31°22'34"—31°23'32"N, 平均海拔735 m, 为低山地区。该区属亚热带大陆性湿润季风气候, 江淮小气候区, 为南北兼有气候特征。该地具有雨量充沛、雨热同季、日照较长、积温较高等特点。太阳年辐射总量96.9—112.5 kcal·m-2, 为湖北全省最高值[18]; 年日照时数1634.4—2153.0 h, 年平均温度16.1℃, 无霜期238—270 d, ≥10℃积温4700—5162℃; 年降雨量多年为1156.2—1688.7 mm。研究区土壤为黄棕壤和黄壤[19]。群落乔木优势树种为黄山松(), 其数量占乔木的40.45%, 生物量占全部乔木的90.00%以上。标准地内还有少量乔木种, 如短柄枹栎()、野漆()、麻栎()和黄檀()等。
2 材料与方法
2.1 标准地设置与数据收集
2016年7月开展标准地调查。选择人为活动干扰程度相对较轻, 且具有代表性的典型黄山松天然次生林4块, 在每个样块设置1个面积为20 m× 20 m的标准地; 对标准地内的木本植物(DBH≥5.0 cm)每木检尺。记录样地地理位置和环境因子(见表1)。记录样地起测木本植物的胸径、树高和冠幅; 记录灌木层和草本层基本情况。
2.2 指标计算方法
2.2.1 偏度和峰度
直径分布的形状可以用偏度与峰度来评价[7]。表示非对称的偏斜方向与偏斜程度,的绝对值越大则表明偏斜程度愈大;>0为左偏;<0为右偏。表示分布曲线的尖峭或平坦程度,>0表示尖峭;<0表示曲线较正态分布平坦。表达式为:

表1 不同标准地黄山松天然林基本情况

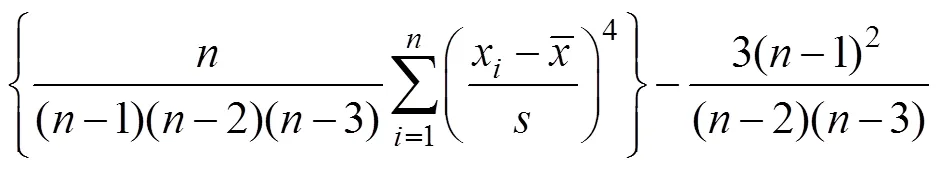
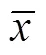
变异系数是直径标准差与算术平均直径的比值。其值越大, 表明直径分布范围越大。

2.2.2 林分直径分布多样性
采用Shannon指数和Simpson指数研究林分直径分布的多样性[20], PieLou指数用于描述群落物种均匀度, 表示物种个体数目在群落中分配的均匀程度, 可用于林木直径在不同径阶的分布状况。
Shannon-Weiner指数:

PieLou 均匀度指数:

Simpson指数:
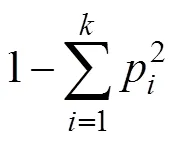
式中:为Shannon指数;为Simpson指数;为林分直径分布均匀度指数;p为每个径阶林木株数n占总株数的百分比;为标准地林木分布径阶数。
2.2.3 林分直径分布模型与检验
根据学者们对不同天然林相关研究结果和黄山松天然次生林的特点, 本研究选择负指数分布、normal分布、lognormal分布、logistic分布和Weibull分布等5种概率密度函数。
2.2.4 数据统计分析
本研究按2 cm标准整化径阶并分级, 数据采用Excel 2013和SPSS 22处理。
3 结果与分析
3.1 偏度与峰度
从表2可以看出, 1—4号标准地黄山松林分起测径级分别为5.00 cm、5.50 cm、5.30 cm和22.00 cm。标准地1林木直径的为0.026, 分布形态接近正态但略左偏, 说明林木分布偏向中间径阶。标准地2和标准地3的为0.078和0.050, 径阶分布形态接近正态但略向左偏, 林木直径也偏向中间径阶; 标准地4的为-0.609, 林木主要分布在较大径阶, 林木直径分布右偏。标准地1直径分布的为0.135, 接近正态; 标准地2和标准地3的分别为-1.366和-1.383, 直径分布形态较标准正态分布更平坦; 标准地4的为1.197, 林分直径分布曲线明显高于正态分布,呈尖峰态, 表明林分中等直径林木的分布相对比较集中[6]。

表2 黄山松标准地乔木统计

表3 SK、KT与林木因子相关分析
注: *<0.05; **<0.01。
3.2 多样性指数分析
由表4可知, 林分直径分布的Shannon指数值为2.200—2.836; Pielou均匀度指数值为0.885—0.947; Simpson指数值为0.871—0.932。多样性指数、均匀度指数和林木径阶数变化趋势完全一致, 即随着林分径阶数的增大, 林木在不同径阶分布的多样性也增大, 各径阶林木分布的数量也更均匀。黄山松林木分布径阶的数量与林木直径分布的多样性变化趋势一致, 径阶越高, 林木分布的多样性也越高, 林木在不同径阶分布的均匀程度也越高。
3.3 直径分布拟合与检验
利用5种概率密度函数, 拟合黄山松天然次生林林木直径分布, 其参数估计值见表5。由于标准地1、2和3林木的形状参数值范围为1<< 3.6, 说明三块标准地林分直径分布为左偏山状曲线; 标准地4黄山松林分的形状参数= 3.669≥3.6, 观测值接近于正态略向右偏山状分布, 与标准地林分直径分布系数的研究结果一致。

标准地1、2和3的径阶范围分别为6—42 cm、6—32 cm和6—46 cm, 标准地4林木直径分布在23—45 cm间。由图1可知, 标准地1、2和3为左偏山状曲线。标准地1林分直径主要分布在16—20 cm范围, 较符合异龄林直径分布特征; 标准地2的林分直径在20 cm分布最集中; 标准地3林分直径分布集中在8 cm和30—36 cm两个区间范围; 标准地4林分直径集中在较高径阶范围, 为37—41 cm, 黄山松林分直径分布为略右偏山状曲线。
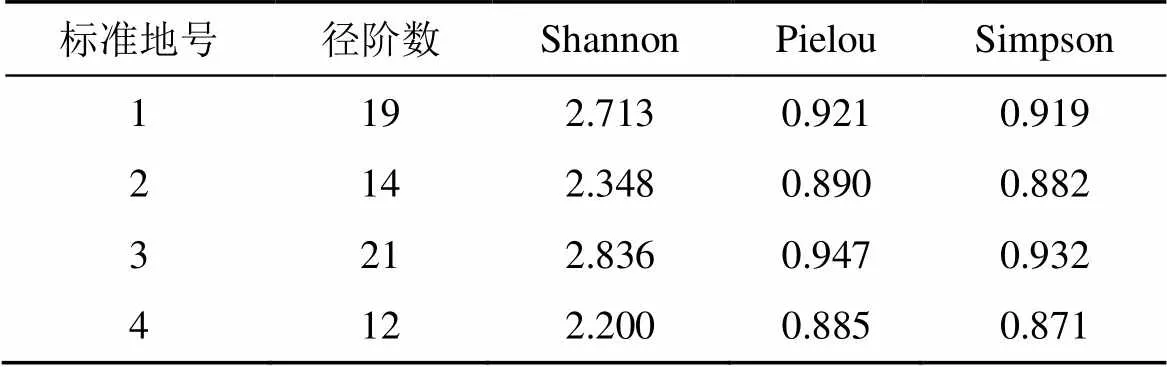
表4 黄山松林木直径分布多样性

表5 黄山松标准地林分直径分布参数估计与检验

表6 黄山松林分直径分布函数检验统计结果
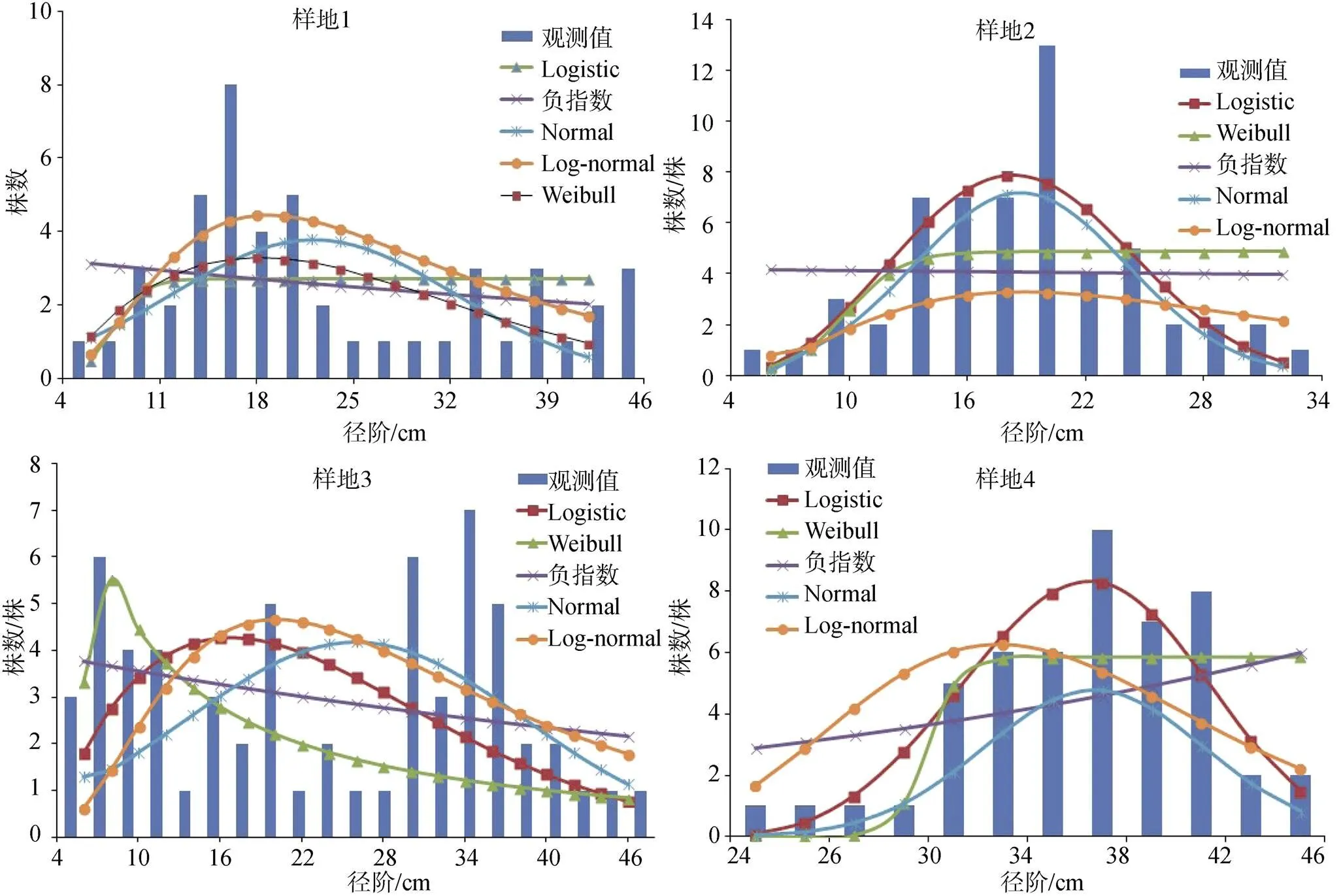
图1 林分直径分布观测值与分布拟合
Figure 1 Observed values and fitting values of diameter distribution of
4 讨论
4.1 峰度与偏度
黄山松天然林林分平均直径较小时,>0, 直径分布主要呈单峰左偏山状, 与陈明久[21]关于黄山松直径分布研究结果一致。林分处于中老龄时,<0, 更多林木集中在较高径阶区间, 直径分布呈右偏山状。在自然状态下, 林分直径的和会随着林分年龄的增长而呈规律性变化[22]。随黄山松天然林林分平均直径D减小, 直径分布更趋于左偏; 林分平均直径D增加, 分布的尖峰态趋势更显著, 林分直径分布离散程度更小, 与石振威等[12]对栎类直径分布的、与林分平均直径分布变化的研究结果一致。
4.2 林分直径分布多样性
Shannon-Weiner指数可用来描述在不同径阶林木个体出现的不确定性。不确定性越高, 分布的多样性也就越高。Pielou指数是基于Shannon-Weiner指数为基础的均匀度, 可以反映林分中不同径阶林木的个体数的分布格局。在研究不同径阶林木数分布格局时, 我们认为Pielou指数可以用以解释林木各径阶个体数目在全部径阶分配的均匀程度。本研究表明随黄山松林分径阶数目增多, Shannon-Weiner指数值升高, 不同径阶之间林木个体分配的Pielou指数增加。Simpson指数越高, 林木直径分布的多样性也越高。本研究中, Simpson多样性指数主要表达黄山松林木直径分布的多样性, 同时也作为不同径阶上黄山松个体数量的多度指标。
群落中的黄山松幼树分布较少, 其分布以黄山松大树和成熟树为主, 这是黄山松采取以大量成年大树提高种群级间失稳率V值以加强竞争的结果[2], 但对于黄山松林分在未来的更新是不利的。根据黄山松林分特征, 利用多样性分布指数变化, 调节林木直径结构, 使林内中小径级林木获得足够资源, 促使小径级林木的正常生长和林下更新[10], 监测林分更新过程中林木直径分布的多样性, 有利于最优林分结构的构建。
4.3 林分直径分布拟合
麻城黄山松天然次生林的恢复中, 随着林木径级结构增大, 黄山松进入群落上层, 对环境中的光照资源的占据能力最大, 需要的其他环境资源也最大, 主宰着群落环境的非对称竞争, 逐渐使得群落结构简单。同时, 郁闭度也是影响天然林下层植物多样性的主要因子[23], 这与其他强阳性树种群落结构特征相同[24]。这种以光环境主导的林内环境, 使得黄山松林分径级差异下降。因此, 江蓝等[25]研究黄山松海拔分布格局时, 按5 cm胸径划分黄山松林分径阶, 显然不能满足不同径阶对分布林木数量上的要求[26]。本研究针对标准地林分直径分布特点, 按2 cm标准整化径阶并分级, 使黄山松直径分布和变化特征更为准确反应林分直径分布特征, 结合Weibull概率函数的高度适应性和灵活性, 得到较好的拟合效果。这也说明了Weibull密度函数可被广泛应用于不同物种的多度分布[27]和林分直径分布拟合[16]。本研究Weibull概率函数能够较好地拟合林木直径不同、不同的山状分布曲线。研究结果与相关学者利用Weibull概率函数对不同林分直径分布拟合结果[16, 28-29]相近, 与陈明久[21]对黄山松天然林林分直径分布Weibull函数拟合的结果一致。
林分直径结构研究, 需要兼顾异龄林对分布函数的适应性和拟合精度的差异性。本研究Weibull函数直径分布拟合精度, 表现出受林分平均直径因素的影响, 其影响可能来自于Weibull函数自身, 也可能来自对直径差异较大林分的取样不足。因此, 可针对黄山松林分直径连续径阶变化, 采用Weibull函数对直径分布进行拟合检验, 并建立林分直径分布预测模型, 为确定林分发展阶段、后期造林设计、建立林分生长和收获模型提供依据。
5 结论
黄山松天然林林分直径主要呈左偏山状分布; 林分直径较大时呈右偏山状分布。黄山松林分径阶数目增多时, 不同径阶林木直径分布的均匀性增加, 林木直径分布的多样性也越高。Weibull分布函数能够较好地拟合黄山松天然林直径分布。
根据黄山松天然次生林林木直径分布特点, 可采取不同的森林经营措施: 第一、对缺乏更新层的大径级林分, 补充黄山松苗木, 提升小直径林木竞争潜力, 合理扩大径阶数, 使直径分布多样性和均匀性得到改善, 避免其单纯林和老龄化。第二、开展科学森林经营,制造有利于天然更新的林窗, 为黄山松林分更新层个体的发育创造良好生境, 以合理的林分密度改善物种多样性, 使大径阶林木的直径分布趋于合理。第三, 在近成熟林阶段, 伐除不良木, 改变大径级纯林高和右偏趋势, 加大直径分布范围, 降低林分, 使黄山松林分更趋于自然化。
[1] 苏松锦, 刘金福, 兰思仁, 等. 黄山松研究综述(1960- 2014)及其知识图谱分析[J]. 福建农林大学学报(自然科学版), 2015, 44( 5): 478–486.
[2] 邢聪, 江蓝, 何中声, 等. 戴云山不同海拔黄山松群落的高度级结构研究[J]. 森林与环境学报, 2019, 39(4): 380– 385.
[3] 李克之. 黔中喀斯特山地森林灌木层结构与功能研究[D]. 贵阳: 贵州大学, 2008.
[4] 惠刚盈, 胡艳波, 徐海. 结构化森林经营[M]. 北京: 中国林业出版社, 2007.
[5] STEPHENSON N L, VAN MANTGEM P J, BUNN A G, et al. Causes and implications of the correlation between forest productivity and tree mortality rates[J]. Ecological Monographs, 2011, 81: 527–555.
[6] 巢林, 洪滔, 李键, 等. 中亚热带不同林龄杉木人工林径级结构与林下物种多样性分析[J]. 植物资源与环境学报, 2015, 24(2): 88–96.
[7] 惠刚盈, 盛炜彤. 林分直径结构模型的研究[J]. 林业科学研究, 1995, 8(2): 127–131.
[8] 汪求来. 广东省针阔混交林直径分布规律研究[J]. 林业调查规划, 2014, 39(6): 28–34.
[9] OBIANG N L E, NGOMANDA A, HYMAS O, et al. Diagnosing the demographic balance of two light-demanding tree species populations in central Africa from their diameter distribution [J]. Forest Ecology and Management, 2014, 313: 55–62.
[10] 李超, 裴顺祥, 张连金, 等. 北京油松人工林竞争指数的适用性评价[J]. 浙江农林大学学报, 2019, 36(6): 1115–1124.
[11] 褚欣, 潘萍, 李琦, 等. 闽楠天然次生林直径分布模拟研究[J]. 江西农业大学学报, 2019, 41(2): 273–280.
[12] 石振威, 曾思齐, 龙时胜, 等. 湖南针栎混交林直径分布及演替动向[J]. 西北林学院学报, 2019, 34(5): 172–178.
[13] 雷娜庆, 铁牛, 刘洋, 等. 兴安落叶松天然林林分直径分布和树高分布[J]. 东北林业大学学报, 2017, 45(1): 90– 93.
[14] MEYER H A. Structure, growth, and drain in balanced uneven-aged forests[J]. Journal of Forestry, 1952, 50(2): 85–92.
[15] LEAK W B. An expression of diameter distribution for unbalanced, uneven-aged stands and forests[J]. Forest Science, 1964, 10(1): 39–50.
[16] BORDERS B E, SOUTER R A, BAILEY R L, et al. Percentile-based distributions characterize forest stand tables. Forest Science, 1987(33): 570–576.
[17] BORDERS B E, PATTERSON W D. Projecting stand tables: a comparison of the Weibull diameter distribution method, a percentile-based projection method and a basal area growth projection method. Forest Science, 1990, 36(2): 413–424.
[18] 董敏. 麻城市生态保护与建设规划研究[D]. 武汉: 华中农业大学, 2013.
[19] 刘力萍, 雍军, 汪洋, 等. 五脑山枳椇天然种群分布格局研究[J]. 林业调查规划, 2019, 44(4): 97–102.
[20] 李超, 闾妍宇, 胥辉, 等. 思茅松天然林林分直径大小多样性及环境解释[J]. 东北林业大学学报, 2016, 44(11): 24–30.
[21] 陈明久. 基于胸径分布模型的黄山松树高分布模型的构建[J]. 宁德师范学院学报(自然科学版), 2018, 30(4): 397–401.
[22] 巢林, 洪滔, 林卓, 等. 中亚热带杉阔混交林直径分布研究[J]. 中南林业科技大学学报, 2014, 34(9): 3l–37.
[23] RIVAIE A. The effects of understory vegetation on P availability inforest stands: a review [J]. Journal of Forestry Research, 2014, 2(3): 489–500.
[24]袁继池, 邱军, 蔡京勇, 等. 红椿天然群落多样性与环境因子的关系[J]. 森林与环境学报, 2017, 37(1): 16–21.
[25] 江蓝, 何中声, 刘金福, 等. 戴云山黄山松种群径级结构的海拔分布格局[J]. 福建农林大学学报(自然科学版), 2019, 48(5): 585–590.
[26] 孟宪宇. 测树学[M]. 北京: 中国林业出版社, 2006.
[27] WANG Y, ZHU S J, LI J, et al. Species abundance distribution patterns of acommunity in Xingdoushan Nature Reserve[J]. Journal of Resources and Ecology, 2019, 10(5): 494–503.
[28] HAARA A, MALTAMO M, TOKOLA T. The-nearest- neighbor method for estimating basal-area diameter distribution[J]. Scandinavian Journal of Forest Research, 1997(12): 200–208.
[29] 陈昌雄, 黄宝龙, 林立法. 南平市延平区天然阔叶林直径分布的研究[J]. 福建林业科技, 2014, 31(1): 1–4.
Diameter distribution of a natural secondaryforest in Macheng City
HOU Mei1, HU Jianmin2, ZHANG Qinqin1,*, WANG Yang1,*
1.,430200,2.,438300,
The target is to study the diameter distribution characteristics and diameter distribution diversities of the natural secondary forest ofin Macheng City, Hubei Province and to establish suitable fitting distribution models. A sample plot survey was made of the natural secondary forest of, and the skewness and kurtosis of the stand diameters (the diameter at breast height or DBH) were researched to explore the traits of diameter distribution curves. Shannon-Weiner index and Simpson index were counted to study the diversity characteristics of stand diameter distribution. 5 probability density functions involving negative exponential function, normal distribution function, lognormal distribution function, logistic distribution function and Weibull distribution function were used to fit the distributions of the stand diameters of, and the fitted functions were verified with chi-square test (2). The result showed that 1) the diameter distribution curves were mainly positively skewed, while the diameter distribution curves were negatively skewed as the diameter class was larger. 2) The diversity and evenness indices of diameter distributions ofwere consistent with the size change of stand diameter classes. 3) The goodness-of-fit of Weibull distribution function had an optimal fitting effect and the acceptance rate of it was 75.0%. The research result can provide references to the prediction of the diameter distributions and growth dynamics ofstands and the guidance of the management offorests.
; natural secondary forestry; diameter distribution; Weibull distribution function
10.14108/j.cnki.1008-8873.2022.01.020
侯梅, 胡剑民, 张琴琴, 等. 麻城黄山松天然林直径分布[J]. 生态科学, 2022, 41(1): 179–185.
HOU Mei, ZHANG Qinqin, WANG Yang. Diameter distribution of a natural secondaryforest in Macheng City[J]. Ecological Science, 2022, 41(1): 179–185.
S791.259
A
1008-8873(2022)01-179-07
2020-06-08;
2020-06-21
湖北省教育厅科学研究计划指导性项目(B2018481, B2018482); 中德技术合作林业科研项目(ZDJSHZ202001)
侯梅(1980—), 女, 湖北潜江人, 硕士, 副教授, 主要从事林业技术研究, E-mail: 36245421@qq.com
张琴琴, 女, 硕士, 讲师, 主要园林技术教学科研, E-mail: 307555802@qq.com
汪洋, 男, 硕士, 教授, 主要从事植物生态学教学科研, E-mail: 13296698026@163.com
