双拉撑矩形截面容器的设计及优化
2022-03-04蒋宾伟
蒋宾伟*
(中海油石化工程有限公司)
0 引言
矩形截面容器的结构较为平整,被广泛应用于储存和运输中低压粉末材料。当容器的长侧边较长时,通常采用增加拉撑的方式来降低侧板的挠度和应力。目前,双拉撑矩形截面容器设计时主要参考GB/T 150.3—2011《压力容器 第3部分:设计》附录A以及ASME Ⅷ-1标准。但二者均规定了标准中的方法仅适用于双拉撑板沿长边侧均布,且拉撑板不承受横向压力作用的双拉撑矩形截面壳体结构,这样限制了拉撑板的设计空间。
某环氧丙烷及丙烯酸酯一体化项目聚醚生产装置中粉末颗粒的捕集器采用双拉撑矩形截面壳体,其设计载荷情况可见表1。本文在GB/T 150.3—2011 附录A 推荐方法的基础上,利用有限元分析方法[1-2]对双拉撑矩形截面壳体进行了设计及结构优化。

表1 设备计算条件
1 设计计算
目前,国内外对于壳体正应力的计算方法大多是基于直梁法的基本假设。设计计算时将侧板的计算模型简化为两端约束受均布载荷的梁[5-6],再通过受力平衡计算出各个关键点处的应力。在双拉撑矩形截面壳体结构中,壳体的轴向力为最大正应力。因此,在设计计算时只需要计算出壳体中的轴向力并加以限制。双拉撑矩形界面容器关键部位的薄膜应力和弯曲应力可按照式(1)计算:
短边薄膜应力:

长边薄膜应力为:
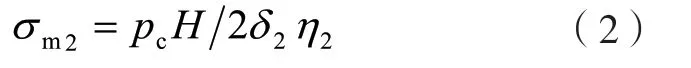
拉撑板薄膜应力为:

短边N 点内壁弯曲应力为:
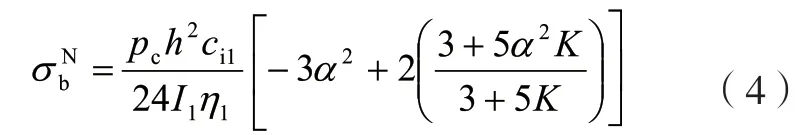
短边Q 点内壁弯曲应力为:
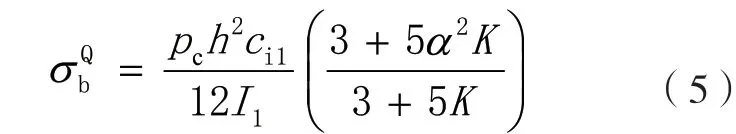
长边M 点内壁弯曲应力为:
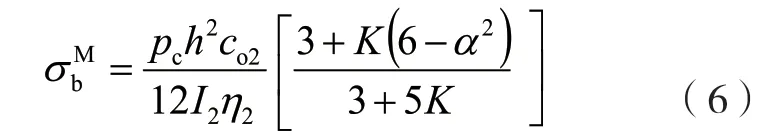
长边Q 点内壁弯曲应力为:
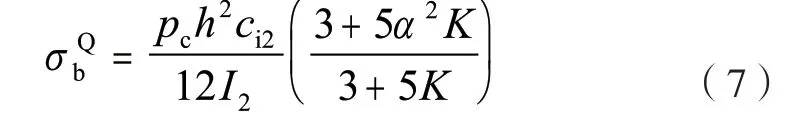
短边N 点外壁弯曲应力为:

短边Q 点外壁弯曲应力为:
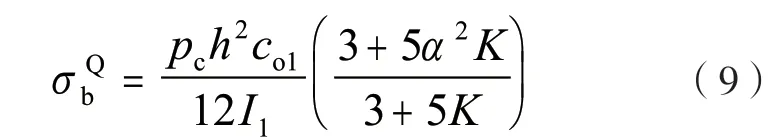
长边M 点外壁弯曲应力为:
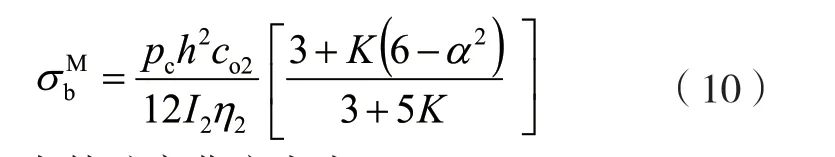
长边Q 点外壁弯曲应力为:

式中:pc——计算压力,MPa;
H——容器内侧短边长度,mm;
h——容器内侧长边长度,mm;
δ1——短边计算厚度,mm;
δ2——长边计算厚度,mm;
δ3——拉撑板计算厚度,mm;
I1——短边单位长度截面惯性矩,mm4;
I2——长边单位长度截面惯性矩,mm4;
ci1——短边板截面中心轴至内壁距离,mm;
ci2——长边板截面中心轴至内壁距离,mm;
co1——短边板截面中心轴至外壁距离,mm;
co2——长边板截面中心轴至外壁距离,mm;
K——系数,K=(I2/I1)。
2 数值模拟
2.1 基本模型及约束情况
双拉撑矩形界面容器为比较规则的容器,具有明显的对称性。在数值模拟计算时应采用二维平面并建立1/4 模型,这样可以显著提高计算效率,同时保证计算精度。计算模型的详细尺寸可见图1,建模时考虑了钢板的负偏差为0.3 mm。

图1 计算模型尺寸详图(单位:mm)
该设备采用奥氏体不锈钢材料,其杨氏模量为195×103MPa,泊松比为0.247。
在矩形截面壳体内侧边施加压力载荷0.7 MPa,在两侧板及拉撑板的对称线上施加位移约束,分别约束对应截面的法向位移。
2.2 网格划分及网格无关性验证
选用带中间节点的四边形面网格(PLANE183),设置厚度值为1 mm。由于计算模型尺寸较为规整,进行网格划分时采用总体网格尺寸作为网格划分控制依据。表2 列出了总体网格控制尺寸分别为1 mm(模拟一)、2 mm(模拟二)、3 mm(模拟三)时3 种网格划分形式的模拟计算结果。网格无关性验证结果显示:当网格尺寸小于2 mm 时,壳体的薄膜应力(最大正应力)基本不再变化,相对于计算值误差的绝对值达到了1.65%,可以满足工程设计需要。

表2 网格无关性验证

图3 应力云图(单位:MPa)
2.3 结果分析
根据数值模拟结果以及理论计算情况,按照图4选择应力线性化路径。从线性化结果中提取最大正应力,最大正应力的提取规则如下(1)薄膜应力取远离结构不连续处,即图4 中路径C1-C2、D1-D2、F1-F2;(2)一次加二次组合应力取在距离内侧线交点2 个节点处。应力强度的最大值发生在Q 和M 点内侧线交点处,但是此处结构不连续造成应力集中较严重,应力线性化过程中,峰值应力对此处最大应力强度的影响较大。峰值应力的特点是衰减较快,其对设备的影响程度有限,在应力评定时安全系数也不同于其他应力。应力线性化结论中,在距离内侧线交点2 个节点处的一次加二次组合应力最大。
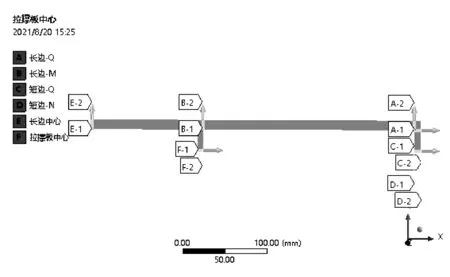
图4 线性化路径
表3 为常规计算和数值模拟得到的两种结果的对比情况。根据表3 可短暂:(1)除了拉撑板薄膜应力外,数值模拟结果均低于常规设计计算值,说明GB/T 150—2011标准附录A中公式的计算结果是比较安全的;(2)在远离结构不连续处,两种结果符合性较好,在结构不连续的拐角附近,数值模拟和理论计算的结果误差较大。这是由于GB/T 150—2011标准附录的计算结果未考虑结构不连续处应力集中情况以及拐角处面积对两侧加强作用的影响。
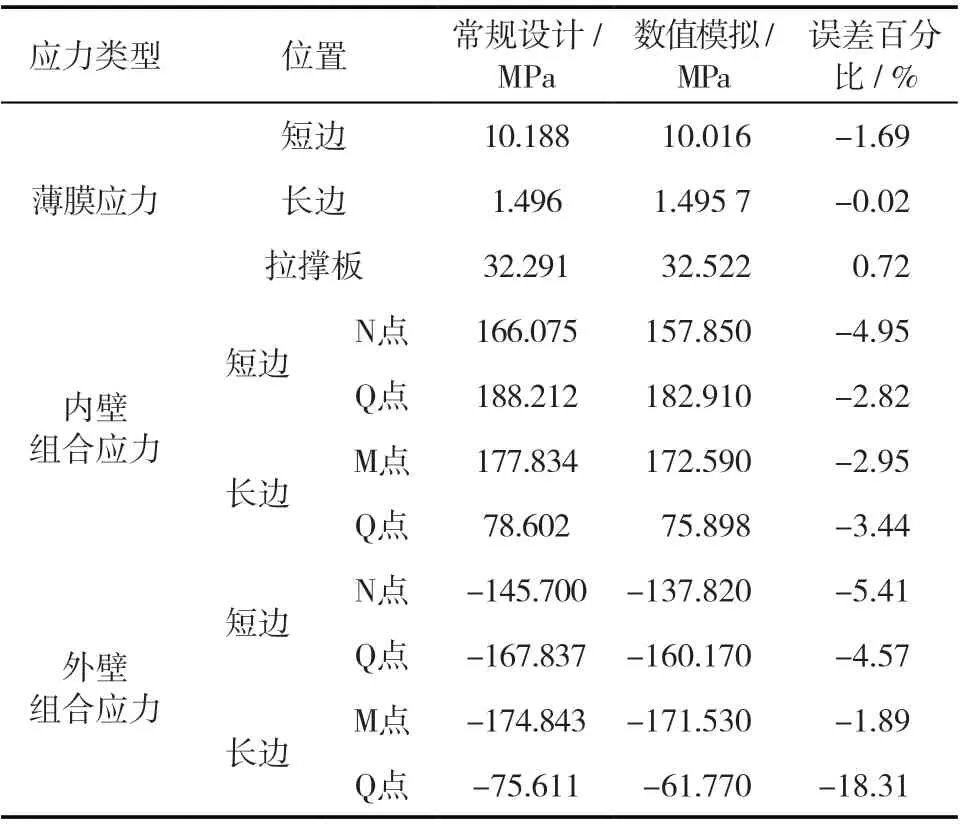
表3 两种计算结果对比
3 结构优化
从原设计的应变及应力云图分析可知原设计存在两个弊端:(1)长边两侧腔体中间部分的应变量达到了0.56 mm,约等于中间腔体部分应变量(即0.17 mm)的3 倍;(2)拉撑板两侧应变不等,导致了拉撑板与长边焊接部位受到弯曲应力作用。基于以上两个特点,在不改变壳体设计总体尺寸的情况下,设计者提出向外移动拉撑板的优化方案:(1)拉撑板外移5 mm;(2)拉撑板外移10 mm,并通过数值模拟的方法进行了分析。表4 给出了拉撑板外移优化后的分析结果。数值模拟结果得到的规律如下:随着拉撑板的外移,Q 点组合应力显著下降,M 点的组合应力增大;随着拉撑板外移,长边两侧腔体中间部分最大应变值显著下降。在保持原设计最大组合应力的情况下,拉撑板向外移动5 mm 时,壳体各个结构的应变较为平衡,材料能够充分发挥其作用;但外移10 mm时,M 点组合应力超出了原设计最大组合应力,因此不建议采用。
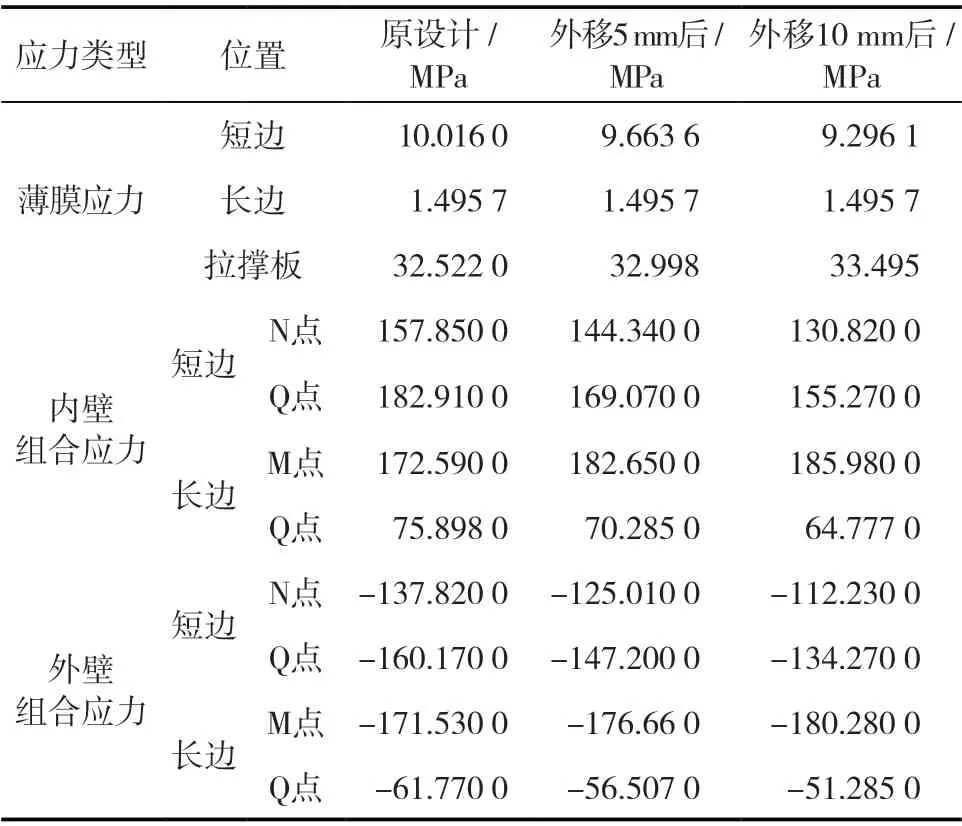
表4 拉撑板外移优化后分析结果
4 结论
本文结合双拉撑矩形截面容器的设计以及数值模拟得出如下结论:
(1)根据GB/T 150.3—2011 附录A 得到的设计计算结果能够较好地反应双拉撑结构的受力情况,得到的应力水平较为准确,可以较好地指导设计。
(2)在原拉撑板均布的基础上,适当调整拉撑板的位置能够有效调节长侧边的受力情况。随着拉撑板外移,边界处的Q 点组合应力显著下降,拉撑点附近的M 点组合应力增大,长边两侧腔体中间部分最大应变值显著下降。
(3)采用ANSYS Workbench 软件进行有限元分析后得到了较为合理双拉撑矩形容器结构。这种方法可以为GB/T 150.3—2011 附录A 使用范围之外的非圆界面壳体设计提供合理化的参考方法。
