基于三维坐标开发的弯管加工程序

杨 林，刘 浩，黄 运

(中车成都机车车辆有限公司，四川 成都 610051)

由于弯管相对于中心线对称，所以可将其看成是由直线段和圆弧段组成[1]，在矢量弯管中，简化成若干条线段进行研究分析。如果将其放入笛卡尔坐标系中，并将各直线延长至相交，相交点用三维坐标(x,y,z)表示，并将各段进行矢量表示，然后利用矢量运算的基本概念和运算法则，研究三维坐标与弯管之间的关系，从而可推导出弯管转化程序的数学公式。并通过编程将数学公式转化为弯管转化程序，实现弯管加工数据的程序化转换，很好地解决弯管设计图样信息不能直接用于车间弯管加工的问题，降低工艺转化错误率，有效提高管路加工准确性与效率。

弯管由若干直线段和圆弧段(弯曲部分)组成，管路四周各点关于中心线(即管子轴线)对称，因此，利用弯管中心线及其弯曲半径[2]，就可以完整描述其三维形状[3]。

1 弯管形状的几何描述

1.1 弯管的模型概述

把弯管两相邻的中心线两端延长至相交，形成交点[4]，通过各点的三维坐标(x,y,z)以及不同管径对应的弯曲半径，就能决定弯管形状，并求出弯管各段的长度、旋转角、折弯角、总长等。管子的弯曲半径是常数，决定管子形状的几何参数主要是弯管两端点与相邻直线段的交点坐标，因此只需找出各直线段相交点的三维坐标，就能通过一系列数学公式计算出弯管程序各项数据。

1.2 弯管的矢量描述

数控弯管机进行弯管加工，通常是从弯管的一端开始，到另一端结束[5]，因此，不考虑弯管的折弯角度，弯管可以看作是几段直线段首尾连接而成，弯管的每一段直线段都可以用代表大小和方向的矢量来表示，空间中的矢量可以用三维坐标(x,y,z)表示，利用矢量的运算原则和计算方法，即可求出弯管的几何参数，如各段的长度、旋转角、折弯角等。矢量示意图如图1所示。

1.3 管路几何坐标表示

假设有1根3段的车下制动弯管，设各直线段相交点依次为P1、P2、P3和P4(见图2)，并规定各点坐标为P1(x1，y1，z1)、P2(x2，y2，z2)、P3(x3，y3，z3)、P4(x4，y4，z4)，可根据相邻直线段交点的空间坐标计算出相邻两点的长度。

2 弯管理论计算过程

2.1 弯管模型代数表示

2.1.1 各段矢量大小

各段矢量计算式如下：

(1)

2.1.2 相邻各段长度计算

每一段直线的长度为：

(2)

式中，i，j=1，2，3，4，j>i。

2.1.3 各段矢量的方向余弦

各段矢量的方向余弦如下：

(3)

(4)

(5)

式中，i，j=1，2，3，4，j>i，k=1，2，3；cosαk、cosβk、cosγk表示各段矢量的方向余弦。

2.2 弯管加工参数计算

弯管加工过程需要管路的各直线段长度、折弯角度、旋转角度和总长度数据。通过矢量的方向余弦，计算出弯管的折弯角；通过矢量长度计算公式，计算出弯管直线段长度；通过面与面的法向量，计算出弯管的旋转角，通过三向量共面的定律，根据值的正负判断旋转角的正负；通过弧长公式L=Rθ，计算出弯管各段圆弧长度。

以图2为例，计算过程如下。

2.2.1 折弯角的计算

δ1=arccos(cosα1cosα2+cosβ1cosβ2+cosγ1cosγ2)

(6)

δ2=arccos(cosα2cosα3+cosβ2cosβ3+cosγ2cosγ3)

(7)

2.2.2 直线段长度的计算

通过图2可知，直线段的距离为相邻两点之间的距离减去切点到交点之间的距离，各段直线在图2中分别为P1B1、B2C1、C2P4，设管路对应的折弯半径为R，具体计算式如下：

(8)

(9)

(10)

2.2.3 弯管旋转角的计算

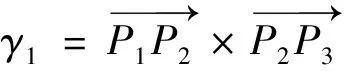
(11)

弯管的旋转角为：

θ1=arccosθ1

(12)

除了计算出旋转角，还应该判定旋转角的正负号，弯管的旋转角分为正向旋转和负向旋转。在弯管机上，顺时针弯管时旋转角为负，逆时针弯管时旋转角为正(0°≤θ≤180°)。而从人的方向看，则方向相反。旋转角的方向通过三向量共面的定律，根据判定值的正负判断旋转角的正负。数值为正为负向旋转，数值为负为正向旋转，计算式如下：

(13)

2.2.4 弯管总长度的计算

弯管是由直线段和圆弧段组合而成，因此弯管的总长度是直线段的总长加上圆弧段而得，计算式如下。

圆弧段长度：

li=Rδi

(14)

总长：

L=|P1B1|+|B2C1|+|C2P4|+∑li

(15)

3 转化程序的实现方式

数学公式在使用时仅仅是一种介质，必须依附于载体才能进行展现，要么依附于表格，要么依附于程序。程序相较于表格，具有可视化、操作性、方便性、快捷性等方面的优势。为便于使用，提高工作效率，笔者利用C语言对数学公式进行编程处理[6]，得到界面简洁、使用方便的“弯管加工程序.exe”。

4 转化程序的使用

“弯管加工程序.exe”界面如图3所示，包括输入区、显示区、结果区3部分。输入区为可输入管路各点的三维坐标(x,y,z)，不同管径对应的弯曲半径R，不同弯管机型号D(用于计算补偿角)[7]，以及设置小数点位数；显示区可显示当前已输入的三维坐标及数值；结果区可显示管路各项几何参数，包括直线段长度、旋转角度、弯曲角度、补偿角度以及下料长度。

应用CAD软件在管路工作图中找到相交点的三维坐标，然后在“弯管加工程序.exe”中输入区输入管路各点三维坐标，填写不同管径对应的弯曲半径，以及不同弯管机型号(用于计算回弹量)，然后点击计算，即可在结果区显示出管路各几何参数(见图4)。显示区、结果区提供复制、粘贴功能，如果需要修改数据，可在显示区直接对数据进行修改，方便快捷，显示区可从Excel表格中复制三维坐标数据，直接粘贴在该区域，结果区的数据也可直接进行复制，粘贴在Excel表格中。

5 转化程序的优势

以往绘制弯管图大多借助工作图，通过不同视图观察以获取弯管长度、角度等信息[8]。这样具有一定的局限性，当弯管折弯处与各正交视图不平行时，通过各个正交视图无法准确确定弯管旋转角，不仅在效率上得不到保证，并且容易出现弯管图绘制错误，导致最后弯管加工程序错误的现象。由于弯管图的绘制具有一定的技术含量，必须经过专业培训才能绘制，所以这种方式不具有普遍性。

而使用弯管转化程序，将弯管三维坐标转化为弯管加工程序，并通过编程的方式实现了弯管加工数据的程序化转换，很好地解决了弯管设计图样信息不能直接用于车间弯管加工的问题，避免了工艺转化的错误率。后续类似的问题均可以通过这种分析方法，实现数据的程序化转换。工艺人员打开程序后可以直接输入弯管三维坐标和弯曲半径，即可得到相应的加工信息，从而很好地解决了工艺转化时费时费力、容易出错的问题，既能提高正确率，又能节省时间[9-10]。

6 结语

弯管加工程序作为弯管加工最重要的载体，而行之有效、准确度高的弯管转化程序可有效保证试制工作的顺利进行。本文通过对管路问题的剖析，将空间三维坐标(x,y,z)与数学中矢量计算相结合，提出一种能够实现高效转换的弯管转化程序，在实践中可省去繁琐的绘图过程，实现弯管加工的程序化计算，提高弯管加工程序的正确率，将在后续项目实施过程中有效提高生产效率。