基于μ综合的弹性体导弹鲁棒控制系统设计

史籍宇 崔颢 陈星阳

摘 要：基于鲁棒控制理论，针对弹性体导弹气动伺服弹性问题开展控制系统研究，通过建立导弹刚性弹性耦合全参数不确定性模型，在传统三回路控制结构的基础上设计了μ综合鲁棒控制系统。 频域分析表明所设计的控制系统具有强鲁棒性，足以应对弹性体导弹的强不确定性。 时域仿真结果表明，μ综合鲁棒控制系统在保证时域指标的同时，相比于经典PID控制系统，弹体一阶振动幅值约为其10%，衰减时间缩短至约0.5 s，有效抑制了弹体的弹性振动。

关键词：μ综合;鲁棒控制;弹性体导弹;气动伺服弹性;振动抑制

中图分类号：TJ765; V211.47  文献标识码：   A 文章编号：1673-5048（2022）01-0047-05[SQ0]

0 引  言

近年来，对导弹速度、射程、机动性等性能的要求越来越高。  设计导弹时只能减小横截面积并增大长度，弹体外形越来越细长化，飞行过程中在气动力和舵面控制力等的作用下，就会产生高频弹性振动[1]。 若设计时不考虑导弹的弹性振动，敏感元件将弹性振动信号引入控制系统，则会产生严重的气动伺服弹性现象，影响导弹的正常使用，甚至发生安全事故[2]。 因此，设计控制系统时考虑弹体的减振控制有着至关重要的意义。

国内外已有大量学者展开了对弹性体导弹的研究。 Choi等[3]討论了气动伺服稳定性问题，在反馈通道中添加自适应滤波器。 张公平等[4]采用模态自适应结构滤波技术，设计了滑模变结构策略。 王雨等[5]提出通过反馈测量信号对弹性振动频率进行实时估计更新的自适应陷波器的设计方法。 李良等[6]基于广义最小二乘法在线估计弹性模态参数，设计了幅值滤波器。 上述研究都将振动看作是一种噪声干扰，在导弹振型频率处引入滤波器对振动信号进行滤除，但导弹的振动模态会受到多种因素的影响，在飞行过程中发生无法预知的变化。 即使采用了在线辨识技术，在有色噪声的干扰下，仍然无法保证在所有情况下得到理想的效果。 Jimenez[7]通过线性二次型高斯回路传递恢复方法设计LQG控制器。 Bibel等[8]采用μ综合设计技术以满足系统的鲁棒性要求。 朴敏楠等[9]提出一种综合相位稳定与线性自抗扰控制的姿态控制器。 上述研究把弹体的弹性振动完全当作系统建模的不确定性来设计控制器，保守性相对较大，在导弹弹性模态剧烈变化的情况下，鲁棒性仍然较差，无法得到满意的效果。

针对上述问题，本文首先建立了弹性体导弹数学模型，将导弹各状态点的弹性振动作为已知，将飞行过程中弹性振动模态大范围无法预知的变化视作有界干扰，基于μ综合鲁棒控制技术设计了控制器，并通过仿真验证了控制器的有效性。

3 仿真验证及结果分析

选取导弹在高度3 km、马赫数1.2的特征点进行仿真设计，各气动参数、弹性模态参数取值如表2所示。

3.1 鲁棒性能分析

对于所设计的鲁棒控制系统，首先应用结构奇异值理论评价其性能，频段选择为0.001～100 rad/s。

3.1.1 标称性能

标称性能是指系统不确定性摄动取0时，控制系统的响应性能，用奇异值来衡量，如图5所示。 奇异值峰值为0.228 01，在此频段内远小于1，满足性能指标。

3.1.2 鲁棒稳定性

鲁棒稳定性是指控制系统在不确定性摄动作用下的稳定性，如图6所示。 峰值为0.399 34，表明当不确定性摄动满足Δ∞<10.399 34时，控制系统满足鲁棒稳定。

3.1.3 鲁棒性能

鲁棒性能是指控制系统在参考信号、外部干扰噪声和不确定性摄动一起作用下的响应性能，如图7所示。 奇异值峰值为0.772 94，控制系统的鲁棒性能达到要求。

3.2 时域仿真分析

在所设计特征点作为标称系统的基础上， 对导弹气动参数和弹性模态参数进行全参数摄动仿真，过载响应如图8所示。 在参数发生大范围变化时，控制系统依然能稳定跟踪控制信号，达到时域性能指标要求，对弹性振动抑制效果明显。

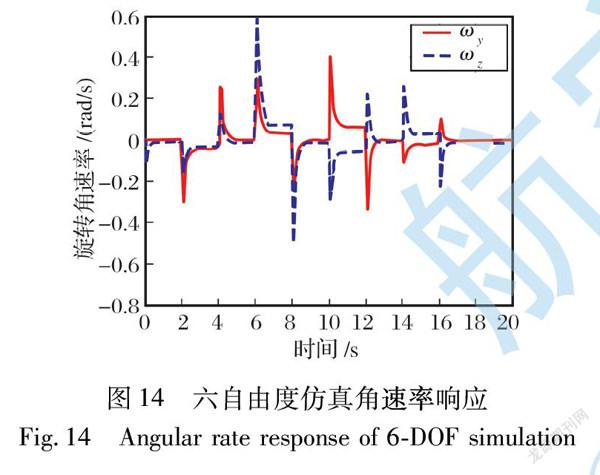
为了进一步对比验证μ综合鲁棒控制系统的控制效果，针对标称系统设计了经典PID控制器，并进行了对比仿真和全弹道六自由度仿真，如图9～14所示。

由图9～12可以看出，由于气动伺服弹性的影响，PID控制系统的过载响应产生了较为严重的振动，舵偏用量更大，控制品质低下，且其激发起的一阶振动响应幅值较大，衰减时间较长。 而本文所设计的μ综合鲁棒控制系统时域指标更优，对弹性振动的抑制效果明显，一阶振动幅值大幅度减小且衰减时间减小到1 s左右，在快速稳定跟踪指令的同时，有效抑制了弹体的弹性振动。 从图13～14中可以看出，μ综合鲁棒控制系统有效抑制了弹体高频振动，全弹道过载跟踪达到设计要求，控制系统达到了优秀的鲁棒性能。

4 结  论

本文针对大长细比导弹弹性振动减振控制问题，提出将各特征点的弹性振动参数作为已知，将弹性参数与其他气动参数在飞行过程中发生的不确定性变化视为摄动，在此基础上建立导弹不确定性数学模型。  基于经典Raytheon三回路结构，优化设计了九摄动鲁棒控制系统，解决了传统控制方法控制效果差且鲁棒性严重不足的问题。 仿真结果表明，μ综合鲁棒控制系统在所有参数摄动的情况下仍能保持稳定，控制效果明显优于经典PID控制，对弹性振动有明显的抑制效果。 但鲁棒控制器的阶次达到了28阶，需进行进一步的降阶研究，在保证控制效果的同时降低系统阶次，解决工程实际应用的难题。

参考文献：

[1] 赵艳辉， 张拥军， 李海峰， 等. 近Nyquist频率情况下的数字化陷波器设计方法研究[J]. 航空兵器， 2021， 28（1）： 104-108.

Zhao Yanhui， Zhang Yongjun， Li Haifeng， et al. Research on Design Method of Digital Notch Filter when Notch Frequency Approa-ching Nyquist Frequency[J]. Aero Weaponry， 2021， 28（1）： 104-108.（in Chinese）

[2] 李越群， 王建. 典型空空导弹弹性伺服控制系统稳定性研究[J]. 兵器装备工程学报， 2018， 39（5）： 35-38.

Li Yuequn， Wang Jian. Research on Stability of Typical Air-to-Air Missile Elasticity Servo Control Sytem[J]. Journal of Ordnance Equipment Engineering， 2018， 39（5）： 35-38.（in Chinese）

[3] Choi H D， Bang H. An Adaptive Control Approach to the Attitude Control of a Flexible Rocket[J]. Control Engineering Practice， 2000， 8（9）： 1003-1010.

[4] 张公平， 段朝阳， 赵艳辉， 等. 战术导弹气动伺服弹性滑模控制技术[J]. 导航定位与授时， 2019， 6（2）： 52-57.

Zhang Gongping， Duan Chaoyang， Zhao Yanhui， et al. Sliding Mode Control Technology of Aeroservoelasticity for Tactical Missiles[J]. Navigation Positioning and Timing， 2019， 6（2）： 52-57.（in Chinese）

[5] 王雨， 崔茅， 张公平， 等. 气动伺服弹性系统的自适应陷波器算法设计[J]. 航空科学技术， 2020， 31（3）： 73-78.

Wang Yu， Cui Mao， Zhang Gongping， et al. Adaptive Notch Filter Design Approach for Aeroservoelastic System[J]. Aeronautical Science & Technology， 2020， 31（3）： 73-78.（in Chinese）

[6] 李良， 李友年， 陈星阳. 基于广义最小二乘法的空空导弹幅值滤波器设计方法[J]. 航空兵器， 2020， 27（1）： 46-51.

Li Liang， Li Younian， Chen Xingyang. Amplitude Filter Design of Air-to-Air Missile Based on the Generalized Least Square Method[J]. Aero Weaponry， 2020， 27（1）： 46-51.（in Chinese）

[7] Jimenez F. Linear Quadratic Gaussian Controller Design Using Loop  Transfer Recovery for a Flexible Missile Model [D].Monterey：Naval Postgraduate School， 1993.

[8] Bibel J， Stalford H. Mu-Synthesis Autopilot Design for a Flexible Missile[C]∥29th Aerospace Sciences Meeting， 1991.

[9] 朴敏楠， 杨志红， 孙明玮， 等. 弹性静不稳定高超声速飞行器姿态综合控制[J]. 中国科学： 技术科学， 2019， 49（7）： 825-839.

Piao Minnan， Yang Zhihong， Sun Mingwei， et al. Attitude Control Synthesis of Unstable Hypersonic Vehicle with Aeroservoelastic Effect[J]. Scientia Sinica Technologica， 2019， 49（7）： 825-839.（in Chinese）

[10] 钱杏芳，林瑞雄，赵亚男. 导弹飞行力学[M]. 北京：北京理工大学出版社，2012：36-45.

Qian Xingfang， Lin Ruixiong， Zhao Yanan. Missile Flight Mechanics[M]. Beijing：Beijing Institute of Technology Press， 2012： 36-45. （in Chinese）

[11] 王潤驰. 弹性飞行器姿态运动建模及控制研究[D]. 哈尔滨： 哈尔滨工业大学， 2017.

Wang Runchi. Attitude Dynamic Modeling and Control for Flexible Flight Vehicle[D]. Harbin： Harbin Institute of Technology， 2017. （in Chinese）

[12] 杨延丽， 陈阳. 基于μ综合方法的导弹鲁棒自动驾驶仪设计[J]. 计算机仿真， 2019， 36（10）： 75-78.

Yang Yanli， Chen Yang. Design of Robust Missile Autopilot Based on μ Synthesis Method[J]. Computer Simulation， 2019， 36（10）： 75-78.（in Chinese）

[13] Zarchan P. Tactical and Strategic Missile Guidance[M]. Washington： Progress in Astronautics and Aeronautics，1994.

[14] 刘慧， 张佳梁， 邵长兴， 等. 基于μ综合的新型空空导弹稳定控制系统控制律设计研究[J]. 上海航天， 2017， 34（2）： 134-143.

Liu Hui， Zhang Jialiang， Shao Changxing， et al. Control System Study for New Air-to-Air Missile Based on μ-Synthesis Method[J]. Aerospace Shanghai， 2017， 34（2）： 134-143.（in Chinese）

[15] Zhu M Y， Wang X， Dan Z H， et al. Two Freedom Linear Parameter Varying μ Synthesis Control for Flight Environment Testbed[J]. Chinese Journal of Aeronautics， 2019， 32（5）： 1204-1214.

Design of Robust Control System for Flexible

Missile Based on μ-Synthesis

Shi Jiyu*，Cui Hao，Chen Xingyang

（China Airborne Missile Academy，Luoyang 471009，China）

Abstract： Based on the robust control theory， aiming at the pneumatic servo elastictiy problem of flexible missile， this paper carries out the control system research. By establishing the missile rigid-elastic coupling full parameter uncertainty model， the μ-synthesis robust control system is designed based on the traditional three-loop control structure. Frequency domain analysis shows that the designed control system has strong robustness and is enough to deal with the strong uncertainty of flexible missile. Time domain simulation results show that， comparing with the classical PID control system， the μ-synthesis robust control system ensures the time-domain index， the first-order vibration amplitude of the missile body is reduced to 10%， and the attenuation time is shortened to about 0.5 s， which effectively suppresses the elastic vibration of the missile.

Key words： μ-synthesis;robust control;flexible missile;pneumatic servo elasticity;vibration suppression

收稿日期：2021-07-14

作者簡介：史籍宇（1996-），男，河南洛阳人，硕士研究生。