低功耗设备常用储能元件的Peukert模型适用性分析

代红丽，张 潇，谢 健，刘 伟，胡顺仁

(重庆理工大学电气与电子工程学院，重庆 400054)

近年来，随着半导体、计算机和无线通信等技术的不断进步，无线传感器网络和物联网技术的应用日益广泛[1]。这类网络的节点通常由低功耗、低成本的无线收发器、微控制器和传感器等元件构成，具有计算能力低、能量开销小等特点。这些低功耗设备可以由储能元件提供正常运行所需的电量，因此更能满足大规模现场部署的需求，特别是在一些难以维护的应用场景[2]。此外，这类设备的工作电流较低，通常小于100 mA，同时为了有效延长使用时间，设备需要在工作/休眠状态之间频繁切换，因此其工作电流并不是恒定的[3]。

低功耗设备常用的储能元件包括碱性电池、锂亚电池和超级电容等。文献[3]指出考虑到部署成本，以碱性电池为主要代表的一次电池往往是无线传感器节点供电的首选。对于环境较为恶劣且对工作时间要求较高(通常以年为单位)的应用场景，锂亚电池更有优势，因为这种电池具有极低的自放电率和极宽的工作温度范围[4]。此外，对于能够从环境中收集太阳能、风能等的应用场景，超级电容由于在充放电次数上的优势已成为可充电电池不可或缺的补充[5]。

为了降低与储能元件维护相关的成本，需要确保每个节点具有尽可能长的工作寿命。为了实现上述目标，有必要根据剩余电量对节点工作进行调度，以充分利用储能元件，从而降低系统的维护开销[6]。常用的剩余电量估计方法包括开路电压法、安时积分法、卡尔曼滤波法以及神经网络法等。然而，这些方法不是需要中断节点的正常工作，就是计算量较大，难以满足节点的实际需求。由于Peukert 模型能够建立储能元件使用时间与放电速率之间的关系，经过适当变形和处理，其亦可用于剩余电量的估计[7-9]。同时，由于Peukert 模型较为简单，这类估计方法非常适合无线传感器节点等低功耗设备。

目前，基于Peukert 模型的估计方法已经被推广到各种储能技术中，比如铅酸电池、氢镍电池[7]、锂电池[8]、超级电容器等[10]。文献[7-9]分别针对氢镍电池、锂电池和超级电容进行了基于Peukert 模型的恒流放电时间估计。在适用性研究的基础上，文献[11]分析了超级电容Peukert 常数与端电压、老化条件和工作温度的依赖关系。然而，现有研究存在三个比较明显的问题：(1)主要面向电动汽车等大电流应用场景和恒定电流(或恒定功率)工况，未考虑低功耗设备所面对的工作模式频繁切换的小电流工况；(2)未考虑碱性电池、锂亚电池等常用的一次储能元件，特别是锂亚电池这种在恶劣环境中常用的储能元件，现有研究几乎没有涉及；(3)主要面向单一类型的储能元件研究Peukert 模型的估计准确性，没有针对常用储能元件进行横向对比分析。

基于此，本文以小电流工况下Peukert 模型对于常用储能元件的适用性为研究目标，通过实验，对比分析了碱性电池、锂亚电池和超级电容的Peukert 模型适用性，所得结果对进一步研究Peukert 模型在小电流工况下的性能具有重要的指导意义。

1 Peukert 模型

Peukert 模型最早用来描述铅酸电池的放电容量随放电电流的变化趋势[9]，指出当放电电流减小时，所释放的电荷量增加。Peukert 模型描述了电池有效工作时间随等效放电电流的变化过程，在放电过程中，等效放电电流I的k次方与有效工作时间t的乘积是一个常数，如公式(1)所示：

式中：I为等效放电电流；t为从初始电压放电至截止电压所用的放电时间；k为Peukert 常数，其取值与储能元件的电化学体系、材料和结构有关；C为一个经验常数。为了得到Peukert常数k与经验常数C，对公式(1)取对数并适当处理，可得：

这意味着，放电时间的对数和等效放电电流的对数成线性关系。因此，通过实际测量储能元件的等效放电电流和放电时间，就可以通过线性回归方法拟合得到Peukert 常数k和经验常数C，从而得到目标储能元件的Peukert 模型。已知经验常数C和Peukert 常数k后，即可根据等效放电电流计算出目标储能元件的有效放电时间。

2 实验

考虑到低功耗设备所面对的工作模式频繁切换的小电流工况，本文选择将储能元件串联不同阻值的电阻进行恒阻放电实验，如图1 所示，利用NI USB-6361 数据采集仪进行数据采集，采样率设置为1 Hz。NI USB-6361 是一款具有16 位精度且支持多通道输入的数据采集仪，其在单通道输入时的最大采样率能达到1 MHz[12]。

图1 恒阻放电实验电路设置

碱性电池、锂亚电池和超级电容三类常用储能元件的主要参数如表1 所示。碱性电池和超级电容的截止电压均设置为0.9 V，以满足节点正常工作的电压要求[3]。考虑到锂亚电池的安全性要求，其截止电压按照数据手册的要求设置为2.0 V[13]。对于超级电容，在每次放电实验之前，使用直流稳压源对其进行足够长时间的充电[9]。

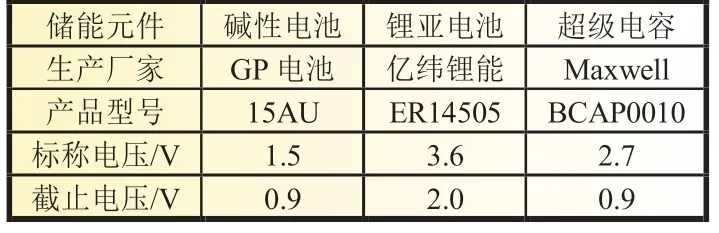
表1 各电路结构的关键指标

为了减小储能元件制造容差的影响，所测试的每类储能元件均选择同一厂家生产的同一批次产品。在放电过程中，NI USB-6361 数据采集仪记录储能元件的端电压变化并传输至PC 端。使用LabView 软件实时显示采集数据，并以TDMS格式的文件进行保存。

对于每类储能元件，选择8 种不同阻值的电阻进行放电实验。由于这三类储能元件的标称起始电压和最大放电电流不同，因此所选择的阻值亦不相同，如表2 所示。锂亚电池可承受的最大持续放电电流为50 mA，因此选取的放电电阻不能低于72 Ω，而超级电容和碱性电池并无此条件限制。在8 组恒阻放电数据中，选择5 组数据用于模型训练，拟合得到对应储能元件的Peukert 常数k和经验常数C，而剩余3 组数据用于对拟合得到的Peukert 模型进行验证。

表2 用于拟合和验证的恒阻放电电阻 Ω

3 实验结果与分析

分别对超级电容、碱性电池和锂亚电池的恒阻放电数据进行处理，得到其等效放电电流与放电时间的关系，如图2 所示，对于三种储能元件而言，随着等效放电电流的增大，放电时间均呈指数下降趋势。

图2 三类储能元件等效放电电流与放电时间的关系

使用Matlab 对所选择的训练数据取对数后进行线性回归，超级电容、碱性电池、锂亚电池的Peukert 模型参数拟合结果如图3 所示，对所得线性模型的斜率取反即可得到Peukert常数k，而线性模型的截距即为经验常数C的自然对数。

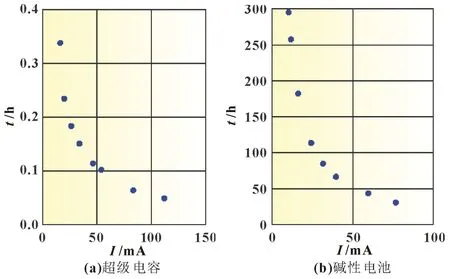
图3 三类储能元件的Peukert模型参数拟合

为了量化拟合效果，分别计算上述线性回归的拟合优度R2。拟合优度R2表示回归方程对观测值的拟合程度，可以取0～1 的任何值，其值越接近1，表示拟合效果越好。超级电容、碱性电池和锂亚电池的拟合优度分别为0.996 0、0.999 4 和0.993 5，均非常接近1，表明拟合效果均很好。根据式(1)和拟合得到的参数，可得超级电容、碱性电池和锂亚电池的Peukert 模型，分别如式(3)～(5)所示：

使用剩余3 组数据对拟合得到的Peukert 模型进行验证，即根据Peukert 模型和等效放电电流计算得到放电时间的估计值，并与实测值进行对比。通过绝对误差和相对误差来评价Peukert 模型的适用性，其计算公式如式(6)～(7)所示，其中，tp是放电时间估计值，tm是放电时间实测值。此外，还计算了两种误差的平均值，如表3 所示，其中，#1、#2 和#3 分别对应表2 中用于Peukert 模型验证的三种放电电阻的阻值。

由表3 可知，就单一储能元件而言，虽然训练数据的等效放电电流范围涵盖了验证数据的等效放电电流范围，但Peukert 模型对不同放电电流的估计误差仍存在较大的差异。从整体来看，在目标工况下，Peukert 模型对这三类储能元件均是适用的。然而，对于超级电容，使用Peukert 模型的估计准确性要低于碱性电池和锂亚电池，其平均相对误差为5.891%，而后两者的平均相对误差分别只有2.898% 和2.931%。超级电容的误差较大，主要是由于自放电的影响。与碱性电池和锂亚电池相比，超级电容的自放电更为显著[11]。当放电电流较大时，放电时间较短，因此自放电的影响可以忽略不计。然而对于小电流恒阻放电工况，由于放电时间较长，因此放电阶段由于自放电而产生的能量损失明显增加。由于Peukert 模型无法描述自放电效应，因此必然会带来较大的估计误差。

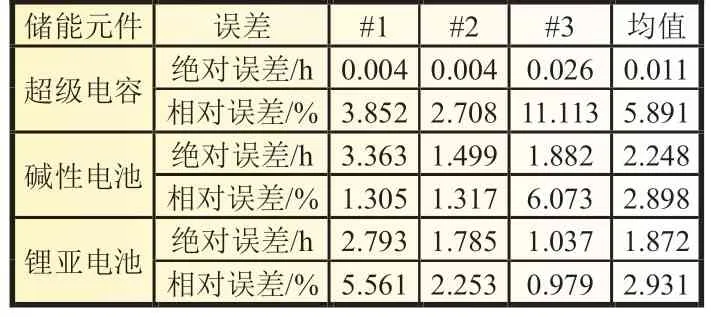
表3 Peukert 模型的验证误差

4 结论

本文通过在小电流工况下对超级电容、碱性电池和锂亚电池进行恒阻放电实验，研究并对比了Peukert 模型对这三种储能元件的适用性。实验结果表明，对三种储能元件进行恒阻放电时，放电时间和等效放电电流之间存在较为明显的指数关系。进一步验证可以发现，使用拟合得到的Peukert 模型对放电时间进行估计时，碱性电池的平均相对误差最小，为2.898%，锂亚电池次之，为2.931%，而超级电容的稍大，为5.891%。这意味着在目标工况下，Peukert 模型对超级电容、碱性电池和锂亚电池均适用。所得结果对进一步研究Peukert模型在小电流工况下的性能具有重要的指导意义。