大规模MIMO系统多用户PSK调制方案的优化*

,

(1.郑州大学 信息工程学院，郑州450001；2.广东省新一代通信与网络创新研究院,广州 510700)

0 引 言

目前机器类通信(Machine Type Communication,MTC)主要包括大规模机器类通信和超可靠低时延(Ultra-reliable Low-latency Communication,URLLC)通信。其中，与4G相比较而言，URLLC被认为是第五代(5G)无线通信最大的创新特征。URLLC主要应用于关键任务场景，它要求链路可靠性能要达到99.999%,端到端时延低于1 ms[1]。在无线通信背景下，如何同时满足系统的低时延与高可靠性能尤其重要。在物理层，为满足超低时延，URLLC的主要特征是进行短数据包传输[2]，此时控制数据(如导频等)的开销不可忽略。如何在较少控制数据开销的前提满足链路的超高可靠性吸引了大量研究者的关注。

大规模多天线技术以其较大的空间分集增益和阵列增益，能够在时延约束下提高无线链路的可靠性；另一方面，大规模多输入多输出(Multiple-Input Multiple-Output,MIMO)的空间复用特点能够实现大规模连接，从而提高系统容量。因此，大规模MIMO被认为是URLLC的使能技术之一[3]。在传统的非相干MIMO通信系统中，酉空时调制在高信噪比(Signal-to-Noise Ratio,SNR)被认为是最优的，但在低SNR中酉星座的可达误差性能有限[4]。Li 等人[5]针对多用户空时调制大规模MIMO系统中，引入绝对加性唯一可分解星座对的概念，提出基于PSK星座的非相干传输方案设计，并说明了当天线数量较大时，在无噪声的情况下发射信号和大尺度衰落系数均是可以唯一确定的，这解决了大规模非相干星座的系统性设计问题。然而，上述方案并没有考虑信号传输对系统超高可靠性的要求。Gao等人[6]为了实现URLLC，在瑞利信道模型下设计出一种基于幅度调制的单用户能量检测框架，并提出一种快速的非相干最大似然解码算法。Popovski等人[7]提出一种大规模MIMO系统上行链路能量检测机制，指出在低信噪比和高移动性情形下，非相干检测相比于相干检测机制具有一定的优势。在不完美信道状态信息(Channel State Information,CSI)下，Zeng等人[8]通过最小二乘信道估计方法对CSI进行估计，并利用估计的CSI对发送信号进行检测，验证了大规模MIMO可支持多个用户实现URLLC。Ren等人[9]研究了上行链路大规模MIMO系统的资源分配问题，提出了低复杂度的迭代算法来解决数据速率最大化问题。需要注意的是，文献[8]与文献[9]中的方案均建立在正交导频开销的基础上，这在短包传输过程中将造成显著的频谱效率损失。本文将利用非正交的导频序列，在大规模MIMO系统下，实现无线信号的超可靠传输方案。

1 系统模型

1.1 多用户大规模MIMO上行链路系统非相干传输方案

本文考虑大规模MIMO上行链路系统，其中在发送端有两个单天线的用户。需要指出的是，大规模MIMO系统中的服务用户数取决于系统可利用的信道次数，本文主要针对5G Node B协议下的两时隙短数据包帧结构来设计多用户空时调制方案。在传统的相干传输方案中，需要首先发送正交导频序列来对信道进行估计，而导频的长度与用户数呈正比。因此，在短包传输方案中，服务用户数将受到极大限制。图1为本文两用户大规模MIMO上行链路系统模型。

图1 系统模型

现假设接收端基站的天线数目为M根，且M≫2；H=[h1,h2]∈M×2为发射端到接收端之间的信道矢量。为实现短数据包传输，假设H每两个符号周期变化一次，且H的具体实现对于发射端与接收端均是未知的，而其概率密度分布是已知的。具体地，本文假设信道hi(i=1,2)服从莱斯分布[9]，即

(1)

式中：Ri代表第i个用户无线信道的莱斯因子;hi,LOS=[1,e-jπsin θi,…,e-jπ(M-1)sin θi]T为天线间距是信号波长一半时的直射路径分量，θi∈(0,π)为第i个用户的波达方向角；hi,NLOS为第i个用户的非直射路径分量，假设其元素是独立同分布的复高斯变量，且均值为零，方差为1。在式(1)中，当Ri=0时，此时的莱斯信道模型则等价于瑞利信道模型。

接收端在两个时隙内的接收信号矩阵Y∈M×2可表达为

Y=HS+N。

(2)

式中：S=[s1,s2]T∈2×2为发送符号矩阵；N服从独立同分布的复高斯分布，其均值为零，方差为

在这里，简要分析莱斯信道下的大规模MIMO系统的有利传播条件。

当θ1=θ2时，可得到

(3)

此时多用户间的有利传播条件不再存在。

而当θ1≠θ2时，

jsin(mπ(sinθ1+sinθ2))}。

(4)

在式(4)中根据三角函数求和性质，在θ∈[0,π]下且θ1与θ2不靠近0与π时满足

(5)

利用式(5)，对式(4)推理可以得到

(6)

因此，只有θ1≠θ2时θ1与θ2不靠近0与π。基于上述分析可以得出结论：在莱斯信道下，为确保多用户信道间的渐进正交特性，可依赖于用户直射路径波达方向角的先验信息对用户进行分组。为不失一般性本文假设θ1≠θ2，然后利用多用户信道的渐近正交特性对接收信号矩阵Y进行运算可得到

(7)

在式(7)中，根据最小欧式距离准则可建立式(8)中的信号检测器：

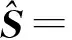
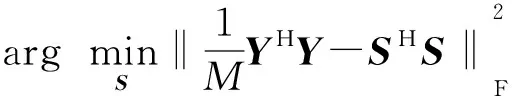
(8)

1.2 基于PSK调制的发射信号矩阵构造

由上文可知发送信号矩阵S包含两用户在连续两时隙内的发送符号。由于PSK星座拥有降低噪声和改善频谱扩展的优势，文献[5]也说明了利用PSK星座进行空时调制可提高系统的通信性能并降低信号估计的复杂度。这里给出本文采用的发射信号矩阵S的具体形式：在第一时隙两个用户同时发送符号1，而在第二时隙两用户分别发送s1与s2，其中s1与s2是基于PSK调制符号，p1、p2与q1、q2分别代表连续两个时隙第一个用户和第二个用户所需要的发射功率。

(9)

(10)

(11)

式中：k代表调制阶数，例如k=2表示4PSK调制符号。基于上述发射信号矩阵以及检测器模型可以得出，要想使系统的误差性能提高，可设计S让不同发送信号相关矩阵的最小距离最大。根据式(8)检测器还可以看出基于欧式距离的非相干检测器模型与S中的五个参数p1、p2、q1、q2、θ有关。为此，下文将针对发射功率与PSK星座结构中的旋转角度θ，建立优化模型以求解最优参数结构。

2 PSK调制方案优化

1.2节中建立的非相干检测器模型，其误差性能取决于信号相关矩阵间的最小欧式距离。本节在此基础上，将优化信号传输方案使星座信号之间的最小欧式距离最大化，以此来提高系统的可靠性能。

2.1 发送信号矩阵之间的最小欧式距离

根据发送信号相关矩阵之间的最小欧式距离最大化的思想，当S1≠S2时，针对五个参数p1、p2、q1、q2、θ建立优化模型:

st. 0≤q1+q2≤2ρu1,

0≤p1+p2≤2ρu2,

(12)

根据1.2中S矩阵中s1与s2的PSK星座结构可以知道，优化模型式(12)中的发送信号分别为

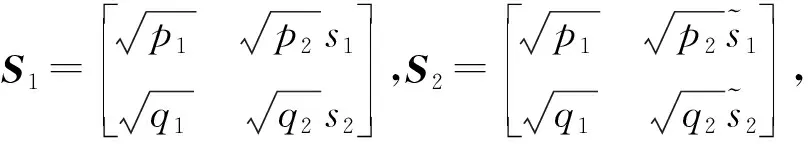
(13)

此时根据发送信号满足S1≠S2可分三种情况进行讨论。

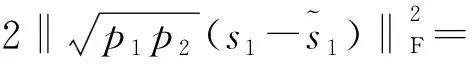
(14)

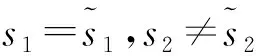
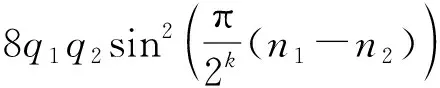
(15)

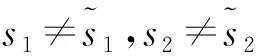
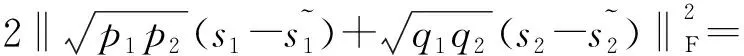
(16)

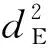
2.2 联合功率分配和旋转角度求解

上节优化模型主要联合发射功率p1、p2与q1、q2和PSK星座结构中旋转角度θ共同优化求解,为了简化优化问题求解，本节将引入四个新的参数对优化问题进行转换。具体地，ρu1与ρu2分别代表用户1和用户2在两个时隙中总的发射功率，让η1与η2分别表示p1与q1占总功率ρu1、ρu2的比例，可以得出p1=ρu1×η1，q1=ρu2×η2，p2=ρu1×(1-η1)，q2=ρu2×(1-η2)。此时，式(12)建立的优化问题模型可等价于

st. 0≤ρu1≤1,0≤ρu2≤1,

0≤η1≤1/2,0≤η2≤1/2,

(17)

对于式(17)，在p1、p2、q1、q2和旋转角度θ的取值范围内利用计算机进行线性搜索，即可得出ρu1、ρu2以及η1、η2和旋转角度θ的最优值。具体线性搜索求解流程如下：

Step1 设置参数ρu1与ρu2，η1与η2和θ取值范围以及步长λ=0.05。

Step2 对五个参数进行五重for循环，得到三种情况下的最小欧式距离。

Step3 在同一个循环空间内从三个距离值中比较出最小值，即mind={d1,d2,d3}。

Step4 对于所有参数取值情况下的最小值进行比较得出最大欧式距离。

Step5 再通过功率转化公式求出p1、p2、q1、q2以及θ值。

根据上述过程利用计算机进行线性搜索仿真，得出了当k=1与k=2时PSK调制方案的最优功率与角度分配的结果，如表2所示。

表2 功率分配与旋转角度结果值

本文重点研究如何构建信号优化目标函数，对于目标函数求解本文初步使用线性搜索算法。然而，需要指出的是，使用群体智能优化算法将加快收敛的速度。

3 仿真与分析

本节通过计算机仿真结果来分析文中所提PSK调制优化方案的误差性能。表3给出了仿真参数设置数据。天线数目M=128的仿真结果如图2所示，可以看出随着信噪比(Signal-to-Noise Ratio,SNR)增大，系统的误符号率(Symbol Error Rate,SER)减小。而且，对比方案文献[5]中的BPSK，当SNR=-10 dB时SER约10-1，此时优化方案SER超过10-3。同时本文提出的4PSK优化方案在SNR=0 dB时，SER约为10-3，而对比方案刚约超10-1，所以优化方案性能要比文献[5]的方案性能有所提高。图3给出了天线数目M=128与M=256(虚线)时各方案的SER，可见在低SNR情况下其四个仿真结果彼此相当，基于BPSK星座的优化方案下SER可达到10-7。

表3 仿真参数设置

图2 M=128的SER和SNR关系图

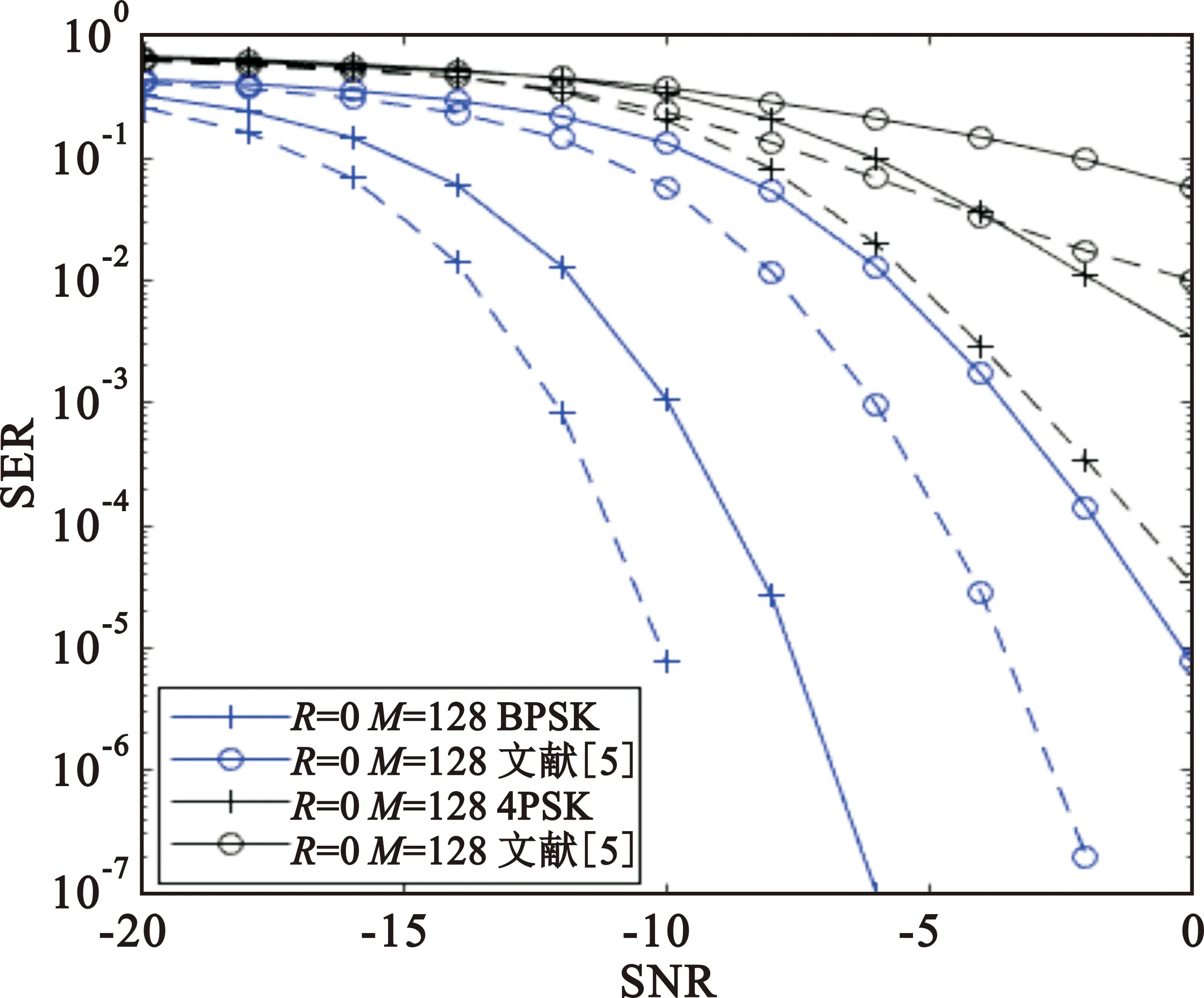
图3 M=128和M=256的BER和SNR关系图

在图4中添加的正交机制方案的具体工作原理是基于正交导频传输方案包含三个传输时隙。首先，在前两个时隙发送正交导频P∈2×2，满足PHP=PPH=I2；第三个时隙发送信号其中x、y是标准PSK调制符号。此时的发送传输矩阵S=[P,s]∈2×3，通过的信道H后，接收端接收信号Z∈M×3可表达为Z=HS+N。标记接收信号矩阵Z的前两列为M×2，基于最小二乘估计方法可得信道估计值为为信道估计矩阵；标记接收信号矩阵的第3列表示为Z3，则基于最大似然准则可建立信号检测器为图3呈现出了上述正交方案的误差性能。

图4 SNR=0 dB时SER和M关系

当SNR值为固定值时，在接收端的天线数目越多系统的性能越好，性能的差距也越明显。如图4所示,在正交机制下的仿真结果要优于非正交机制，但本文提出的优化方案是针对URLLC中短数据包传输通信，只需要两个时隙，适用于信道快速变化的背景。同时图4还给出了SNR=0 dB时四种方案下的SER仿真结果，其中对比文献[6]则是采用PAM星座的非相干ML检测机制，当调制阶数为1时与本文中BPSK星座方案做对比，调制阶数为2时与4PSK星座映射对比参考。根据仿真结果可以分析出在BPSK中SER达到10-3只需要16根天线，而对比文献[5]则至少需要将近40根天线才可达到，文献[6]中2PAM则需要32根天线；在4PSK方案中,优化方案在M=128时SER可达约10-3，而对比文献[5]只能达到约10-2，文献[6]还未到10-2。

图5显示了SNR分别等于0 dB与-5 dB的情况下当天线数目M变化时SER的趋势图。可以观察到，在文献[5]中天线数目为16根时，BPSK星座的误差性能增益可达到约11 dB，4PSK中天线数目达到128根时，本文提出的方案比对比方案约有10 dB的误差性能增益。

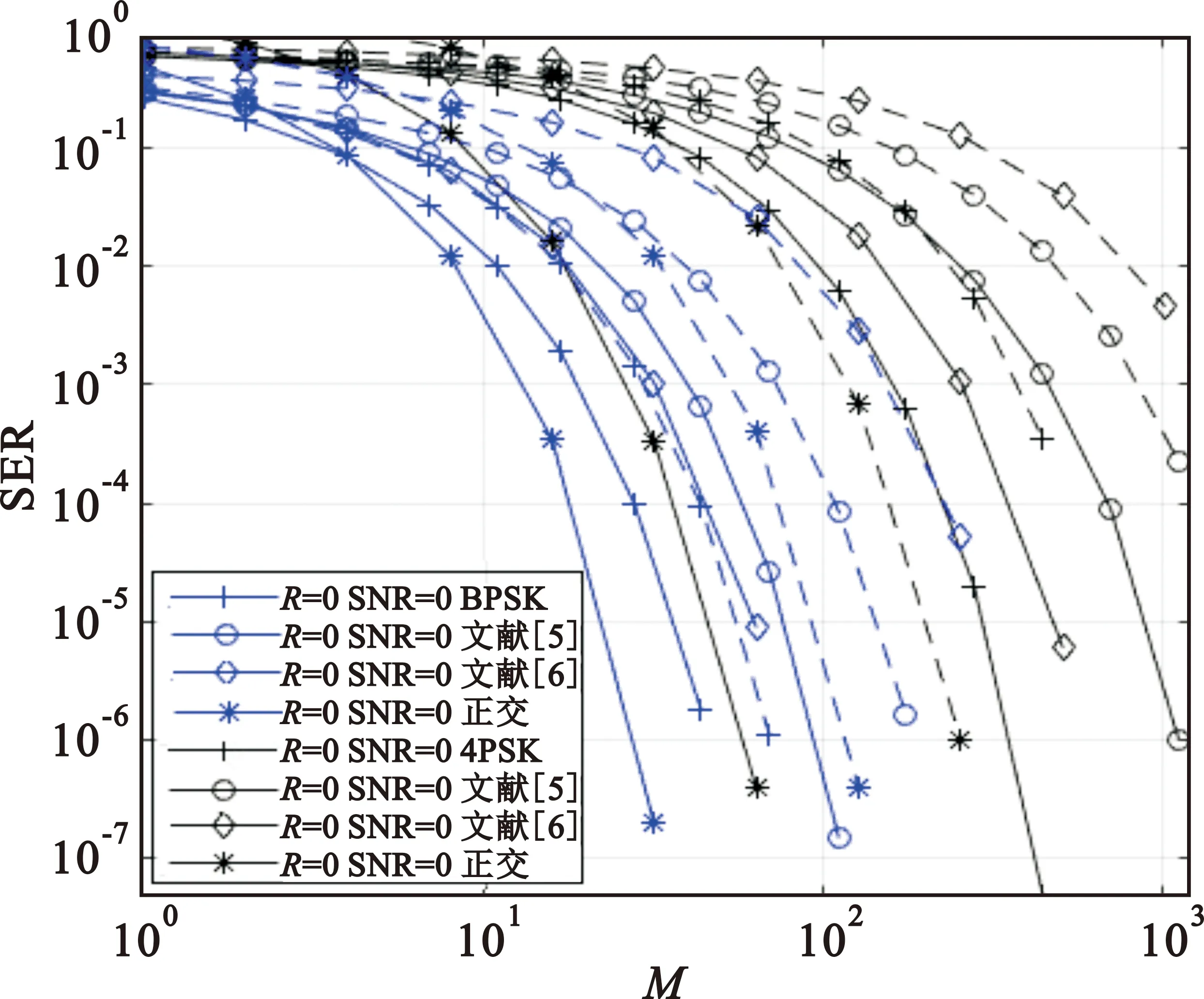
图5 SNR=0 dB与SNR=-5 dB的M和SER关系

图6给出了莱斯信道下不同的莱斯因子对其性能的影响，Ri=0时信道模型为瑞利信道。从图中也可以得出随着莱斯因子Ri(R1=R2)的增大，本文提出的基于4PSK星座优化方案下的性能会提高。

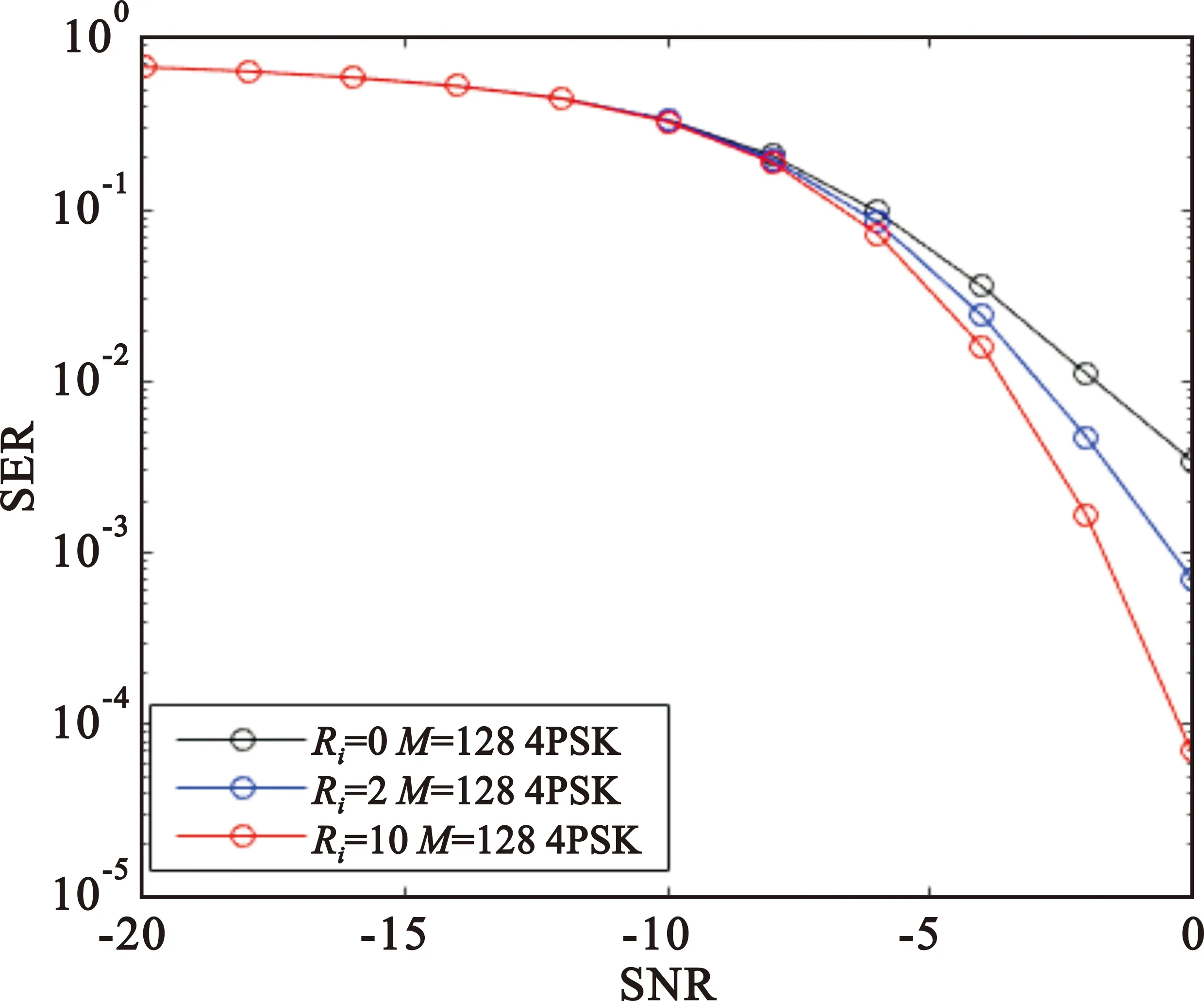
图6 莱斯信道M=128时SER和SNR关系

4 结 论

为了满足URLLC低时延与高可靠性能两大性能指标，本文研究了一种大规模MIMO系统下的非相干信号检测模型。首先针对接收端提出基于欧式距离测度准则的非相干检测器，其中用户端的发射信号是由PSK调制方案来设计信号结构;然后根据信号矩阵间最小欧式距离最大化的思想建立联合优化功率与旋转角度模型，再根据优化模型利用计算机进行线性搜索，计算出传输方案的最优参数值；最后通过计算机仿真分析和验证了所提方案的可行性。