水下绞笼式挖沟机机械开挖数值分析

王 亮，李军营，卢正超，尚智敏，季春光，张其一

1.海洋石油工程股份有限公司，天津 300456

2.天津市精研工程机械传动有限公司，天津 300409

3.中国海洋大学工程学院，山东青岛 266100

海底管道是海洋油气田开发中输送油气资源的重要设施，为维持其自身安全和在位稳定性，免遭拖网渔具等的损害，必须埋设到预定的深度[1]。根据海床的开沟成型方式，常用的挖沟机技术主要有四种类型：机械挖沟法、水力喷冲法、机械和水力结合法、管道自埋法。欧美国家在海床挖沟方面积累了大量的工程经验，比如SMD公司、IHC公司、Forum Perry公司等[2]。我国在海床挖沟设备的研发上起步较晚，目前以挖沟犁和喷冲式挖沟机为主，大部分挖沟机自身无动力，需要拖船辅助施工，很难完成深水区域硬质海床的挖沟任务[3]。随着我国海洋强国战略的推进，海底管道挖沟设备将迎来巨大的挑战。

Bang等人对二维平面定点射流问题进行了研究，结合黏塑性理论得到水流相与泥沙相的通用控制方程[4]。钱忠东等采用了欧拉多相流模型，开展了大量的冲刷研究[5]。孟然利用Flow-3D软件对喷冲式挖沟机挖沟过程进行数值模拟，得到冲刷时悬沙浓度分布及底沙冲刷情况[6]。顾磊等采用耦合的欧拉-拉格朗日方法 （ALE）计算了射流冲刷砂土和黏土的问题[7]。Huang等采用离散单元法开展了三维流体力学计算，分析了射流规律对海床冲刷坑的影响[8]。Machin对海底挖沟机的设计现状进行了总结，指出目前对射流侵蚀深度的预测方法主要是根据土力学中的承载力理论，在土体性质分析中，除剪切强度外，土体的抗拉强度和液塑性质也对其有很大的影响[9]。

本文采用非线性流固耦合理论，利用Abaqus的CEL数值方法，对水下绞笼式挖沟机进行了详细的计算，其一求解挖沟过程中绞笼对土体的切削作用与破土机理；其二给出简洁、高效的绞笼切削阻力计算公式；其三给出准确的拖轮横向拖曳力计算公式。

1 数值模型

1.1 欧拉大变形数值算法

在数值计算过程中，传统的拉格朗日分析法适用于小变形情况，材料与网格节点绑定并充满网格，计算过程中节点与材料绑定，外部荷载作用下网格单元发生变形；当荷载突变或量级较大时，单元网格将会发生畸变，从而导致数值计算无法收敛。

采用欧拉-拉格朗日算法时，计算过程中网格节点在空间中固定，物质材料能够在网格内部流动，即使材料发生过大扭曲，单元网格也不会发生变形，所以数值计算过程中具有较好的收敛性。非线性有限元软件Abaqus结合了二者的优点，采用了耦合的欧拉-拉格朗日（CEL）方法，可以通过分析欧拉材料的体积分数（EVF）来跟踪其流经网格的情况，克服了传统有限元分析方法在处理大变形问题上的困难。两种计算方法示意图如图1所示。

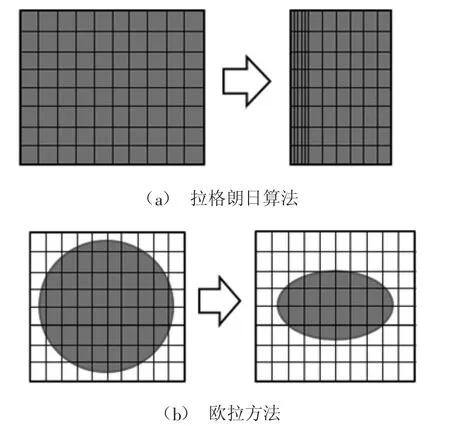
图1 拉格朗日法和欧拉法的变形分析

数值计算过程中采用能量守恒方程，CEL算法采用空间导数的形式描述，而拉格朗日算法则采用物质导数来描述，空间导数与物质导数间映射关系如下：

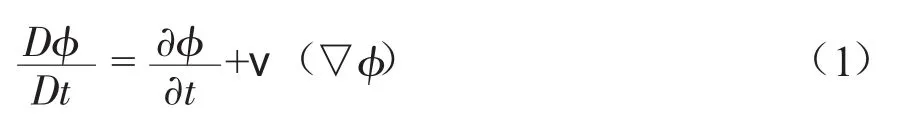
根据式（1）应用于物质导数表示的连续、动量、能量守恒方程，可以推导出空间导数表示的Euler方程组：

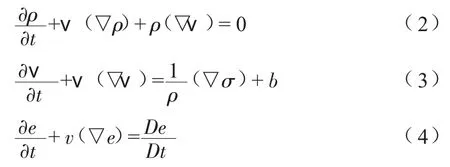
式中：ρ为密度；σ为柯西应力；b为体力；e为单元体积内能。

1.2 模型建立

绞笼式挖沟机有限元网格模型如图2（a）所示，包括：前置6个机械式绞笼切削装置、后置大口径喷冲装置、尾部抽吸扬泥臂。数值计算过程中，绞笼式挖沟机采用小变形的拉格朗日弹性材料进行模拟。

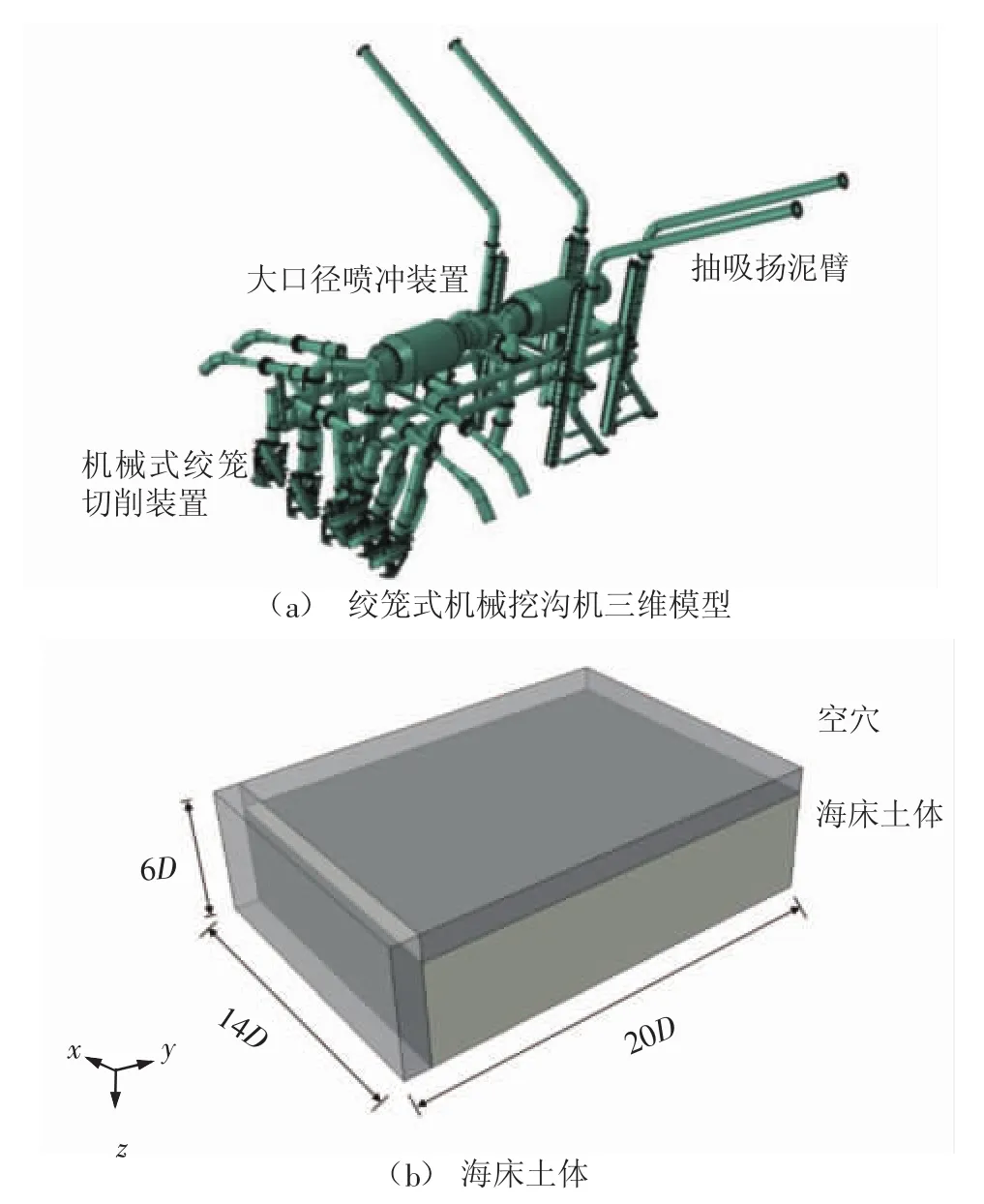
图2 绞笼式挖沟机有限元模型

海床土体设定为欧拉体，如图2（b）所示，采用上述CEL算法进行求解，土体本构关系采用Mohr-Coulomb模型，土体参数如表1所示。在挖沟过程中，由于绞笼的旋转切削作用，绞笼周围土体会发生隆起与扩散，故在海床土体顶部设置空隙层，以避免土体的边界流出；土体模型宽度取为14倍的绞笼直径D，长度取为20倍的绞笼直径，高度取为6倍绞笼直径。数值计算过程中，采用速度边界条件对海床土体施加速度约束，在绞笼旋转轴上施加既定的角速度来实现绞笼对土体的切削作用，欧拉材料与拉格朗日体之间的相互作用使用通用接触对来定义。

表1 海床土体模型参数

1.3 模型验证

为了确保数值求解结果的准确性，需要对数值模型的网格类型与节点数量进行对比试算，同时合理调整数值模型的边界条件。本文计算过程中，通过多次调整单元类型、节点数量与网格密度，最终选择了网格单元数目为2 985 618，单元类型为EC3D8R来进行数值仿真计算。试算过程如表2所示。

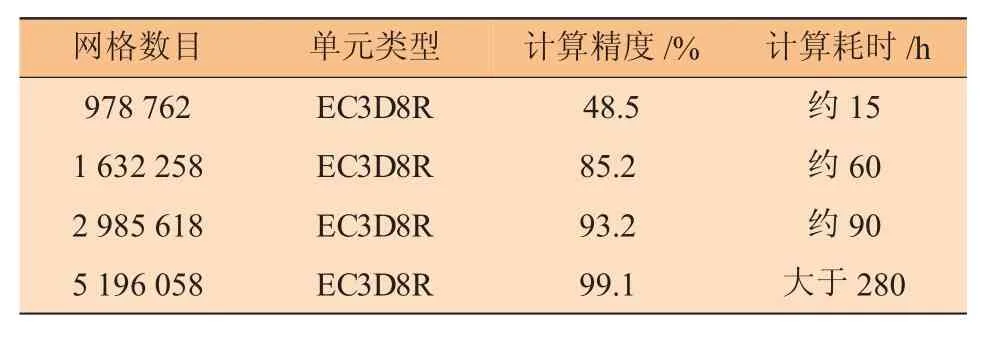
表2 数值网格验证

2 数值计算

为了较为准确地对绞笼挖沟过程进行模拟，分析土体的变形规律与绞笼的切削阻力，本文采用了图3所示的4套绞笼模型进行计算。

图3 三维绞笼

图3所示的4组绞笼中，图3（a）包含了升料螺旋板、弧形导料板、螺旋刀臂和连续刀刃；图3（b）包含了弧形导料板、螺旋刀臂和连续刀刃；图3（c）由螺旋刀臂和连续刀刃构成；图3（d）为卸除了螺旋升料板优化后的绞笼。

2.1 土体变形规律

在绞笼旋转切削作用下，绞笼钭齿前方土体被切削破碎，切削土层塑性应变如图4所示。

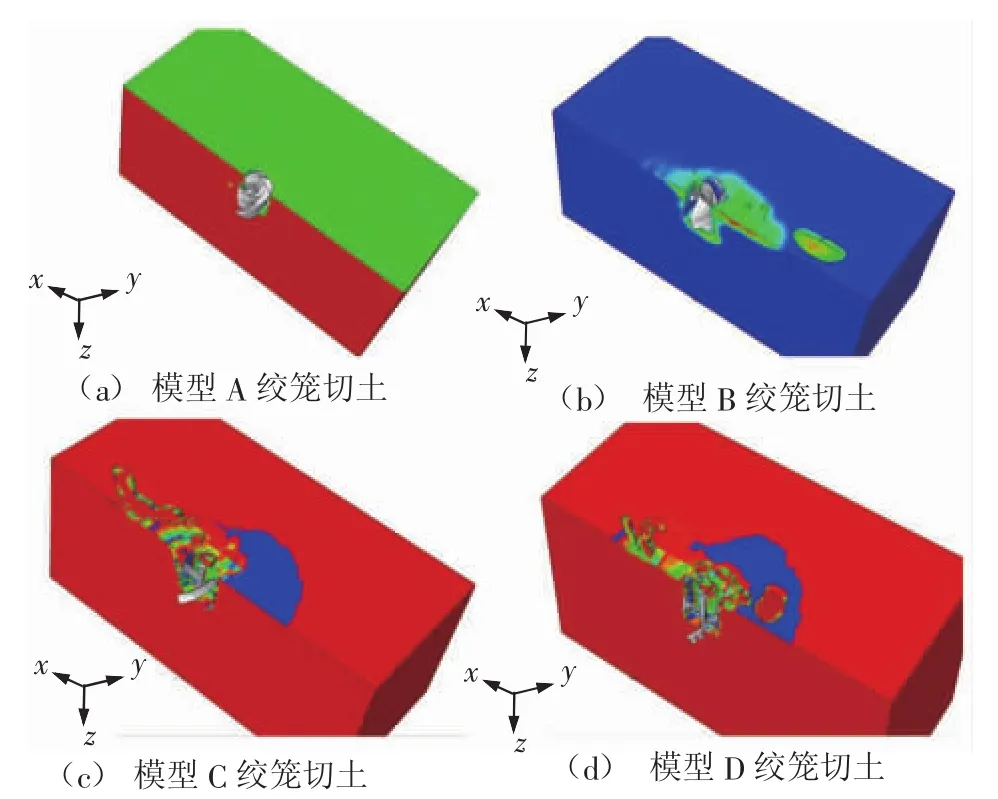
图4 绞笼切削土层塑性应变

根据图4（a）计算结果发现，在绞笼升料板存在较大摩擦系数的情况下，容易出现切削土料堵塞绞笼的情况；大量计算结果表明，当将升料板的摩擦系数降低（极限值为切向摩擦系数设为0），绞笼的水平切削力降低比较明显。根据图4（b）计算结果发现，当拆除升料板后，绞笼切削下来的土体不再受到升料板的摩擦约束，切削土料能够顺利地从绞笼排出，这种情况下的绞笼挖沟过程所需要的水平切削力较小。由图4（c） 计算结果可见，当同时去除升料板和导料板后，绞笼切削后的土体成条状，对土体产生的破碎效果较弱，所以绞笼中的导料板需要保留，用于进一步破碎土体。图4（d）计算结果显示，将连续的一字刀刃更换为离散的刀齿后，绞笼挖沟过程中破碎土体的效果更为明显；相比一字刀刃而言，离散刀齿更适合破碎较为坚硬的海床。当采用模型D绞笼，海床中的挖沟效果如图5所示，图5给出了绞笼切削土体的塑性米塞斯（Mises） 应力。

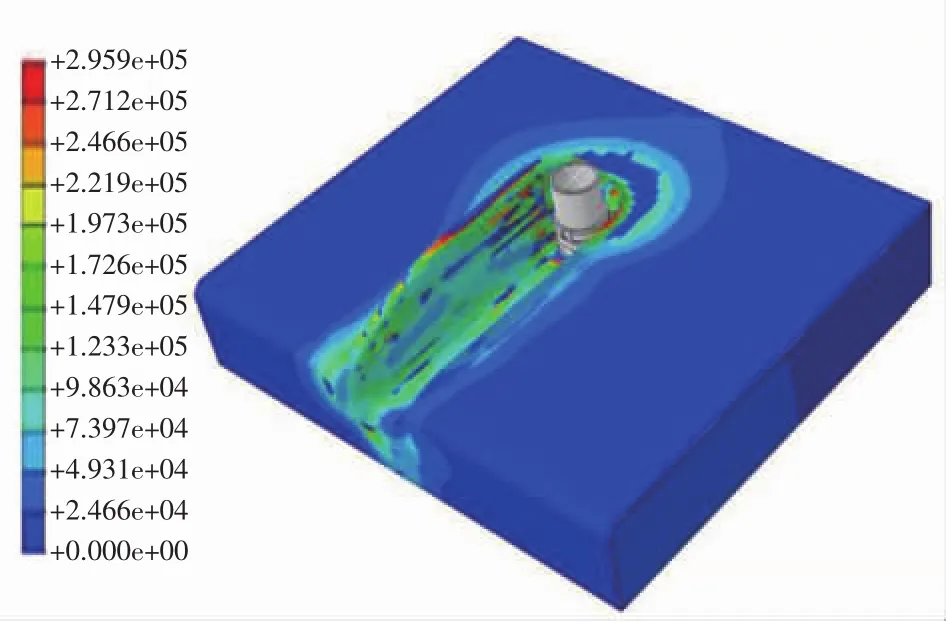
图5 单绞笼开沟米塞斯应力/Pa

2.2 绞笼切削阻力

为了研究绞笼切削转速、挖沟机横移速度(水平行进速度)对切削阻力的影响规律，针对绞笼挖沟机5种水平行进速度和7种不同的绞笼转速，开展了35个工况的数值求解，数值求解结果如图6所示。为了更为方便地计算绞笼的水平切削力，对计算结果进行了归一化处理，即将水平切削力除以海床土体强度抗剪Su和绞笼横截面面积A（水平切削力单位为N、横截面面积单位为m2、海床土体抗剪强度单位为Pa），所以图6纵坐标表示无量纲的数值。

图6 绞笼切削阻力计算曲线

大量数值计算结果表明，绞笼的旋转角速度直接影响着绞笼切土过程中的切削荷载，也影响着拖船对挖沟机的水平拖曳力，本文给出绞笼切削荷载经验计算公式：

式中：Q为绞笼切削阻力，N；Vx为绞笼挖沟机横移速度（水平行进速度），m/s；n为绞笼旋转速度，r/min；A为绞笼横截面积，m2；Su为土体抗剪强度，Pa。

将式（5）给出的计算值与本文数值计算结果进行对比，对比结果如图7所示，对比结果显示本文给出的经验公式能够较为准确地求解绞笼式挖沟机的切削荷载。

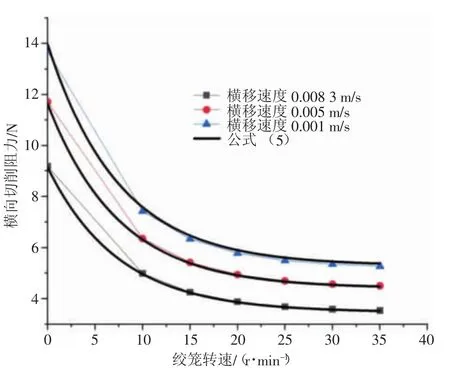
图7 经验公式与数值计算结果对比

3 结论

本文基于欧拉-拉格朗日大变形算法，对绞笼式机械挖沟机在海床的作业过程进行了数值求解，分析了绞笼开沟过程中钭齿前端土体的变形规律，同时求解了土体对绞笼的切削阻力，得出的主要结论如下：

（1）绞笼式挖沟机作业过程中，绞笼转速越快，刃板上的钭齿切削土层厚度越小，所产生的切削阻力越小，同时绞笼的水平拖曳力也越小。

（2）本文给出的绞笼切削阻力经验计算公式，能够快速、准确地预估绞笼切削阻力，能够为工程实际提供参考。