波致海底边坡稳定性影响研究
2022-03-03靳嵩
靳 嵩
中国石油大港油田对外合作项目部,天津 300451
海底滑坡是严重影响海洋油气及海上风电等海洋开发活动的地质灾害之一。促使海底边坡失稳的因素比较复杂,其触发因素包括重力、波浪、地震、快速沉积、水合物分解等。其中波浪会使海床产生周期性变化的瞬态应力场,当它足够大时,就会引起海底土层的滑移;而周期性变化的剪应力会引起海床中残余孔压的升高,导致非黏性土海床的液化和黏性土强度的衰减。波浪不仅减弱海工结构物基础的强度,还增加海工结构物的横向荷载与倾覆力矩。在固定式海洋平台、防波堤设计、海底管道铺设中,都要考虑海床对波浪的响应问题。波浪和海流引起的海床变形及其稳定性是海洋工程设计中必须考虑的重大问题[1]。
上世纪70年代美国因卡米尔飓风产生的波浪诱发了海底滑坡,造成墨西哥湾Southpass70区块多座油气平台不同程度的破坏,因而波浪动态载荷影响下的海床稳定性问题才逐渐得到重视。目前国际上已在海床波压力计算、超孔隙水压力变化规律、边坡稳定性分析[2]等方面取得了一定的成果。对于考虑波浪影响的海洋边坡分析通常按照无限坡进行分析,这与海底滑坡的大部分形态是相适应的,尤其与深水边坡失稳规律类似,然而这并不适用于浅水大坡角边坡,例如因地层沉降、海洋基坑开挖及海底采砂形成的边坡。
1 边坡稳定性评价方法
与陆上滑坡不同,海底尤其是深水海底滑坡通常发生在非常平缓的斜坡上,如挪威Storegga滑坡坡角为0.55°~1.32°,我国南海北部陆坡(存在较多滑坡发育)坡角为3.0°左右。对于海底小坡角斜坡,大部分文献按照无限坡模式利用极限平衡法进行稳定性分析。
无限坡模式为较简单的边坡稳定性分析模型,通常当滑动面近似平行于坡面,且滑坡体的厚度远小于其滑动长度(一般滑坡体的长度与厚度之比大于10)时,可将其作为无限坡进行分析[3],波致无限坡边坡稳定性计算示意如图1所示,计算公式见式(1)。

图1 波致无限坡边坡稳定性计算示意

式中:F为滑坡稳定性安全系数,无量纲;R为土抗力,N;Tw为波浪产生的土剪应力部分下滑力,N;为重力产生下滑力,G为重力,N;Cu为土体抗剪强度,Pa;τ′为波浪产生的土剪应力,Pa;γ′为土浮容重,N/m3;zs为滑裂面土深度,m;β为斜坡坡角,(°)。
因人为挖沙、基坑开挖等因素导致的海底斜坡,其坡角通常较大。当坡角较大时,波浪产生的土体竖向及水平向应力都会对滑移力产生影响,促进海底滑坡发生,因此大坡角斜坡不仅考虑波浪产生的土体剪切应力,同时要考虑土体竖向及水平向应力的影响。可采用两种方法进行计算:一是理论分析方法,采用Yamamoto的理论结果[4],将横向、竖向和剪切应力添加到条块上按照极限平衡方法进行计算;二是有限元方法,直接将海床波压力施加到海床上采用强度折减法进行稳定性分析。
Yamamoto将海床视为均质多孔弹性介质,通过理论分析得到无限深海床应力场的如下简化计算公式:
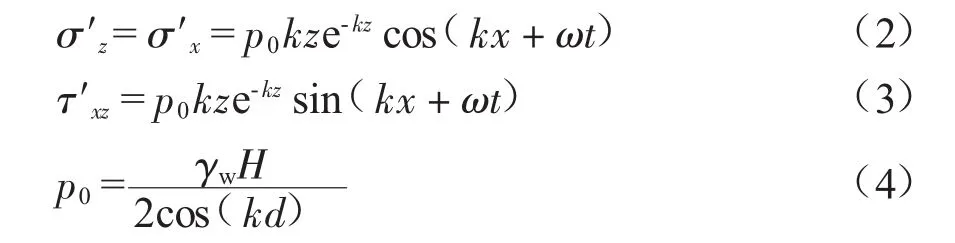
式中:σ′z、σ′x、τ′xz分别为海床面以下某深度处土体的波致竖向正应力、水平正应力以及波致剪切应力,Pa;p0为海床表面波浪压力幅值,Pa;k为波数,m-1;z为海床下深度,m;x为水平向坐标,m;ω为波浪角频率,rad/s;t为时间,s;γw为水的容重,N/m3;H为波高,m;d为水深,m。
从以上公式可以发现在波峰处出现最大竖向正应力,而此时水平向正应力最小;在波谷处出现最大水平正应力和最小竖向正应力。可见在一定坡角情况下,同一时刻水平及竖向正应力对边坡稳定性的影响是不同的,需要分析不同时刻边坡的稳定性,尤其是波峰、波谷等工况下的边坡稳定性,寻找最小安全系数作为边坡稳定性的安全系数。
以强度折减法为代表的有限元法是近些年逐渐流行起来的边坡稳定性计算方法。

其中:CF为折减后的黏聚力,Pa;C为土的实际黏聚力,Pa;Fs为折减系数;φF为折减后的内摩擦角,(°);φ为实际土体摩擦角,(°);τF为折减后的抗剪强度,Pa;σ为法向应力,Pa。
除此之外,强度折减法的边坡稳定性分析还可以以云图的形式给出滑裂面及滑坡体的形态和位置,如图2所示。

图2 强度折减法计算出的滑移面
2 基于强度折减法的波致边坡稳定性分析
采用强度折减法进行波致边坡稳定性计算时,可以采用2种方法处理波浪载荷的影响:一是将Yamamoto波致海床土体应力场以土应力场(水平应力场、竖向应力场及剪应力场)的方式施加到土层中,同时需要计算从波峰到波谷不同时刻安全系数以确定稳定性安全系数;二是将海床波压力施加到海床表面,直接计算不同时刻的安全系数。
从上述分析可看出,极限平衡法及强度折减法都可以进行波致边坡稳定性分析,但强度折减法可对分层土进行稳定性分析,应用范围更广,因此本文采用有限元的第二种方法探讨波致边坡稳定性及不同坡角、土层参数和波浪参数下的边坡稳定性。
海床波压力计算公式见式(8)。根据波高、水深和周期值,可通过牛顿迭代法计算出波长[4-11],计算公式见式(9)。
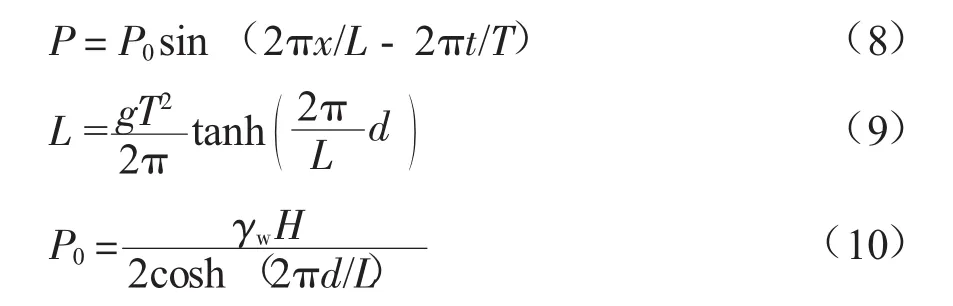
式中:P为海床波压力,Pa;P0为波浪引起海底压力变化的幅值,Pa;L为波长,m;T为波浪周期,s;g为重力加速度,m/s2;d为水深,m;γw为海水容重,N/m3;H为波高,m。
从式(8)、式(10)中可以看出,海床波压力随水深和位置而变化,在不同位置的值是不同的,而且深度越深值越小,有限元模型需按照波压力公式(8)、(10)进行施加,施加结果如图3所示,其中箭头越长值越大,从图中可见同一深度处波压力值在波峰波谷间变化,而且深度越深压力值越小,其分布与理论结果一致。

图3 波压力分布
3 算例
以我国某海域实际工程地质条件进行波致边坡稳定性分析,该斜坡坡角最大接近23°,最小坡角2°,分析采用摩尔-库伦土体本构模型,黏性土按照不排水条件下的总应力进行分析。模型中所有的单元均采用平面应变实体单元,土参数选取该海域边坡土参数,部分土参数如表1所示,波浪选取该海域某台风季实际波高及波周期。所建立有限元模型如图4、图5所示,其中图4坡角为23°,图5坡角为4°。

表1 我国某海域边坡土参数

图4 有限元模型(坡角23°)

图5 有限元模型(坡角4°)
计算坡角为23°时的安全系数曲线如图6(a)、(b)所示,可以发现,在考虑波浪情况下,边坡安全系数明显降低。同时从图6(c)、(d)可看出滑坡体大小虽有差异,但差异不明显,主要是因为该地层存在砂层,滑裂面位于黏土与砂层交界面,坡体大小主要受土体分层及土体物理力学特性影响。

图6 坡角23°时边坡稳定性计算结果
从强度折减方法计算波致小坡角斜坡(4°)失稳的结果可发现安全系数由2.56降低到1.54,虽然在该波浪载荷作用下斜坡失稳风险较低,但安全系数大大降低,可见波浪对边坡的稳定性有非常大的影响。坡角4°时的滑坡体如图7所示,可以看出坡角较小时,滑裂面同样位于黏土与砂层交界面上,但滑坡体体积明显增大。
通过对同一土质特性及波浪条件下不同坡角的波致边坡稳定性分析,可以发现:安全系数FOS随着坡角增大而降低,但并非呈线性关系,而近似为双曲余弦倒数分布,这与不考虑波浪情况下的边坡稳定性不同,分析其主要原因是海床波压力与水深是双曲余弦倒数关系,因而安全系数随着深度降低会急剧降低,当坡角较大时,水深变化梯度更显著,安全系数变化会更明显一些,如图8所示。

图7 坡角4°时边坡稳定性计算结果

图8 波浪作用下不同坡角安全系数
4 结束语
海底滑坡对海洋油气、海上风电等工程开发会产生巨大影响。波浪产生的海床波压力是导致边坡发生失稳的重要因素之一,本文通过对无限边坡及大坡角边坡的稳定性方法适应性对比分析,得到如下结论:
(1)当考虑波浪载荷影响时,无限坡的边坡稳定性方法只考虑了波浪产生的土体剪切应力,而忽略了其产生的土体竖向及水平向应力的影响,这在坡角较小情况下可行,但不适用于大坡角的边坡稳定性分析。
(2)坡角较大时,波浪产生的土体竖向及水平向应力都会对滑移力产生影响,促进海底滑坡发生,因此对于大坡角斜坡不仅要考虑波浪产生的土体剪切应力,同时要考虑土体竖向及水平向应力的影响。
(3)可采用两种方法进行计算,一种是基于Yamamoto的理论结果,将横向、竖向和剪切应力添加到条块上按照极限平衡方法进行计算;另一种是采用有限元方法,直接将海床波压力施加到海床上,采用强度折减法进行稳定性分析。
(4)通过工程实例计算发现,在考虑波浪情况下边坡安全系数明显降低,滑坡体没有明显差异,主要是因为该地层存在砂层,滑裂面位于黏土与砂层交界面,坡体大小主要受土体分层及土体物理力学特性影响。
(5)安全系数随着坡角增大而降低,但并非呈线性关系,而近似为双曲余弦倒数分布;安全系数随着深度降低会急剧降低;当坡角较大时,水深变化梯度更显著,安全系数变化会更明显一些。
