长输供热管网摩擦阻力系数的计算方法研究

刘雪萌，谢英柏

（华北电力大学 动力工程系，河北保定 071003）

0 引言

随着供热规模的扩大，长输供热管网已经在石家庄、银川等城市得到了工程实施和应用［1］。管网规模的扩大，意味着管网复杂性的增加，管网输送能量损失的变化也更为繁杂。因此，如何保障管网的水力安全［2-8］具有重要的现实意义。

长输管网输送的能量损失主要用于克服摩擦阻力［9］。摩擦阻力损失的准确计算，对于合理确定管道设计流量和相关配套措施极为关键［10-11］。Colebrook-White公式是湍流状态下，沿程阻力损失中摩擦阻力系数公认最为准确的计算方程［12］，但Colebrook-White公式是隐式方程，求解过程极为繁琐［13］，因此，众多学者针对Colebrook-White公式的近似解，提出了几十种改进方法。

ĆOJBAŠIĆ 等［14］使用遗传算法改进了摩擦阻力系数的计算模型，提出的2个显式公式其最大误差分别为0.008 3%和0.002 6%。BRKIĆ等［15］利用比Lambert函数更加精确且高效的Wright ω函数得出了一种显式求解方法，其误差不超过0.009 6%。BIBERG［16］则使用截断级数展开法代替Lambert函数解中的数值不稳定项，该方法的最大误差为0.153%。PRAKS等［17］结合Padé逼近和符号回归提出了一种有理逼近方法，计算结果与Colebrook-White公式结果的相对误差不超过0.866%，且计算速度约为利用Wright ω函数求解速度的2倍。长输供热管网与常规供热管网相比，具有输送距离远、管径大、供回水温差大等特点。长输供热管网从热源到主要负荷区的输送距离超过20 km，主要为输送干线，摩擦阻力损失大部分来自于沿程损失。考虑到规模经济性以及管道材料的耐高温特性，长输供热管网的设计供水温度通常为120～130 ℃，设计回水温度为20～40 ℃，供回水温差在80～100 ℃之间。管径一般选用DN1 200～DN1 600，管内流速一般在0.5～3.5 m/s，处于湍流区。NIAZKAR等［18］将56个Colebrook-White公式的近似公式应用于常规管网摩擦阻力系数的计算，研究公式的精确度和收敛问题，结果表明有15个公式精度较高且不存在收敛问题。但是目前对于这种超长距离输送管道摩擦阻力损失的研究还很少。

因此，本文研究Colebrook-White公式其近似公式在长输供热管网的应用，以方便、准确计算摩擦阻力损失。在设计阶段，有助于分析建设中继泵站、隔压换热站的数量和位置，保证管网的可靠性。在运行阶段，有助于判断水击、汽化、超压等危险工况，规避损失，保证管网安全运行。

1 Colebrook-White公式及其近似公式

管道输送的沿程阻力损失采用Darcy-Weisbach公式表示。式中摩擦阻力系数λ的计算式，即Colebrook-White公式为：

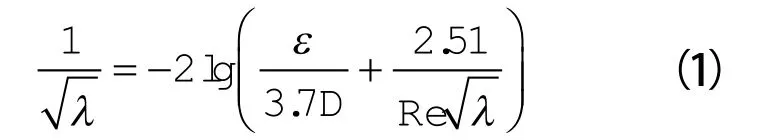
式中λ——摩擦阻力系数；

ε—— 管道内壁当量粗糙度，mm，取ε=0.5 mm；

D——管道直径，mm；

Re——雷诺数。

Colebrook-White公式适用于4 000＜Re＜108，0＜ε/D＜0.05的满流管道。

根据长输供热管网的特点，本文比较选取了文献［14-17，19-28］中的20个经验近似式。

上述方程均表明：摩擦阻力系数λ是雷诺数Re、当量粗糙度ε和管径D的函数。运动黏度υ和流速u是影响雷诺数Re的重要因素。对于长输供热管网，运动黏度随压力的变化见表1，随供回水温度的变化如图1所示。

表1 运动黏度与长输供热管网压力的关系Tab.1 Relationship between kinematic viscosity and pressure of long-distance heating network

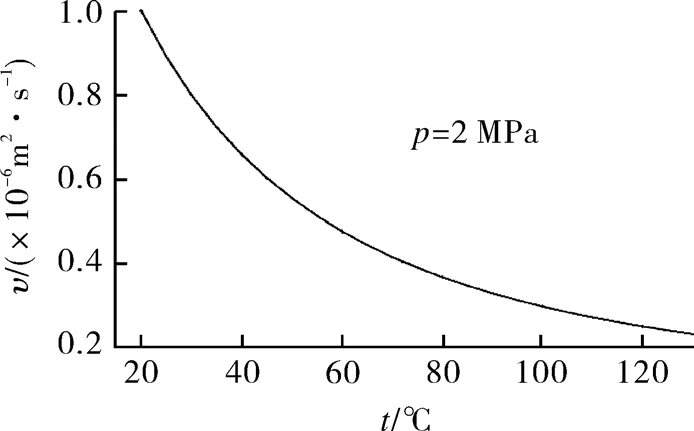
图1 运动黏度与长输供热管网温度的关系Fig.1 Relationship between kinematic viscosity and temperature of long-distance heating network

从图可见，在长输供热管网常见的20～130 ℃温度范围内，水的运动黏度随温度升高而单调下降。但如表1所示，在常见的0.5～2.5 MPa压力范围内，温度相同时，压力对运动黏度的影响极小。因此，本文只研究管道压力2 MPa时，最高供水温度130 ℃，最低回水温度20 ℃情况下的摩擦阻力系数。所有相关的计算参数取值范围见表2。

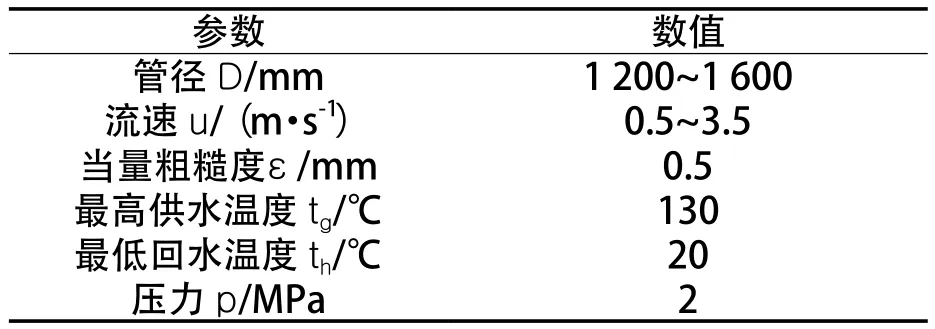
表2 计算参数的取值范围Tab.2 Value range of calculation parameters

2 结果分析

在表2计算参数范围内，得到的流动雷诺数分布情况如图2所示。可以看出，雷诺数分布在6×105～2.456×107之间，属于Colebrook-White公式的适用范围。

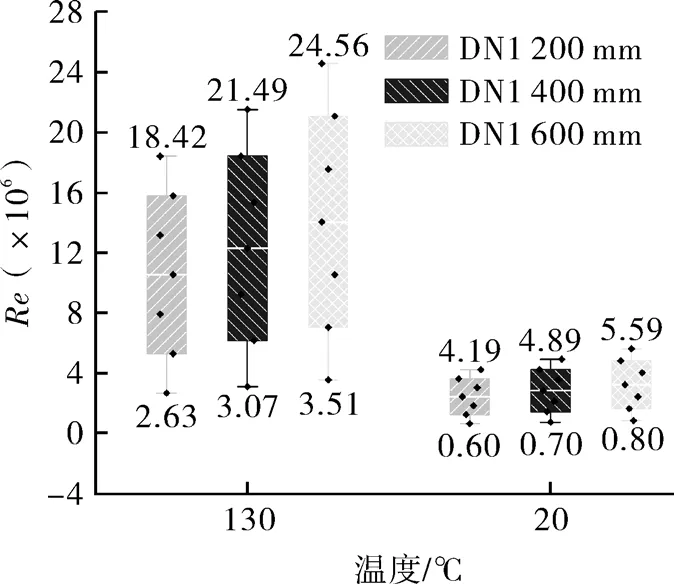
图2 雷诺数的分布范围Fig.2 The distribution range of Reynolds number

若将近似式的计算值记为λ，Colebrook-White公式的迭代值记为λ0，则每个近似式的相对误差计算公式如下：

在最高设计供水温度130 ℃下，改变管径、流速中20个近似式的相对误差分布如图3所示。其中约20%的公式误差非常接近0，约30%的公式误差集中在-0.06%附近，其余的公式误差点散落分布在-0.08%～0.38%之间。当流速越低，雷诺数越小时，个别公式的误差出现了较明显的变化。

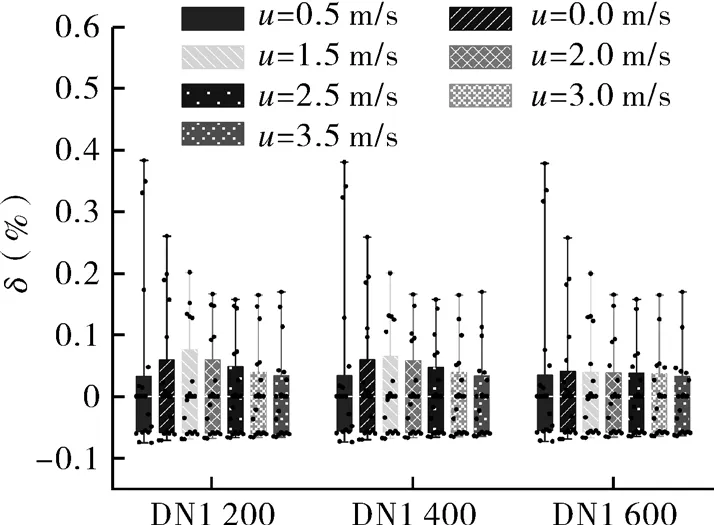
图3 130 ℃时各近似式的相对误差Fig.3 Relative error of each approximation formula at 130 ℃

在最低设计回水温度20 ℃下，改变管径、流速，计算并观察20个近似式的相对误差。误差的分布情况如图4所示，总体上看，误差的分布区间大于130 ℃时的分布区间，20个公式的误差点散落在-0.48%～0.78%之间。约25%的公式误差集中在-0.06%附近，约20%的公式误差集中在0附近。其中，流速在3～3.5 m/s时，仅有3个公式的误差非常接近0。

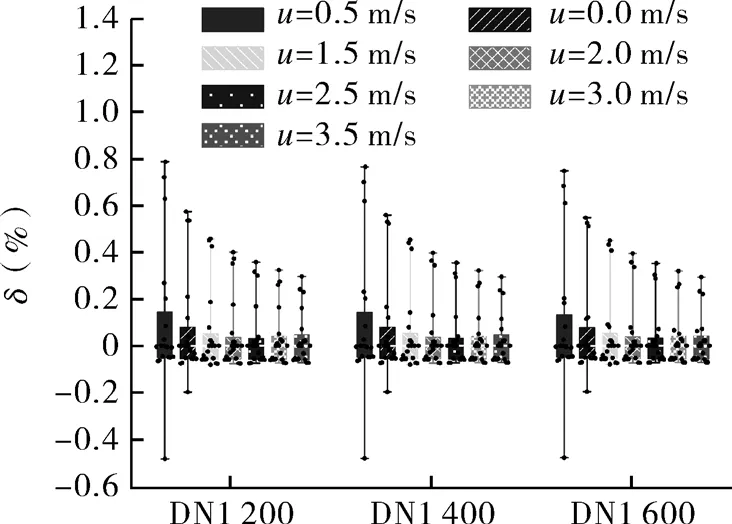
图4 20 ℃时各近似式的相对误差Fig.4 Relative error of each approximation formula at 20℃

综合图3～4可以发现，在长输供热管网的设计供回水温度20～130℃之间，有部分近似式的相对误差受温度变化的影响较小，受管径、流速变化的影响也不明显，始终与Colebrook-White公式的迭代值非常接近。

最后，本文选取这3个相对误差最小的近似式，分别在1/3 200≤ε/D≤1/2 400（即管径为DN1 200～DN1 600），5×105＜Re＜2.5×107的范围内，计算各个近似式与Colebrook-White公式的相对误差。

如图5～7所示，管内相对粗糙度ε/D相同时，各近似公式的误差绝对值随雷诺数增大而减小。在不同相对粗糙度下，Serghides-b的最大误差为0.006 6%，而Biberg公式和Serghides-a的精度始终非常高。

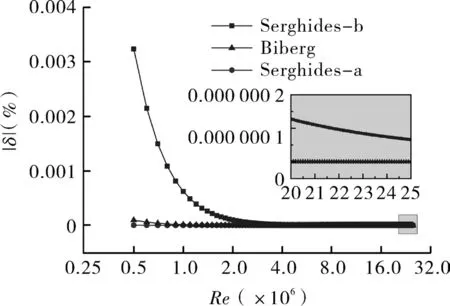
图5 ε/D=1/2 400误差随Re的变化Fig.5 Variation of error with Re for ε/D=1/2 400

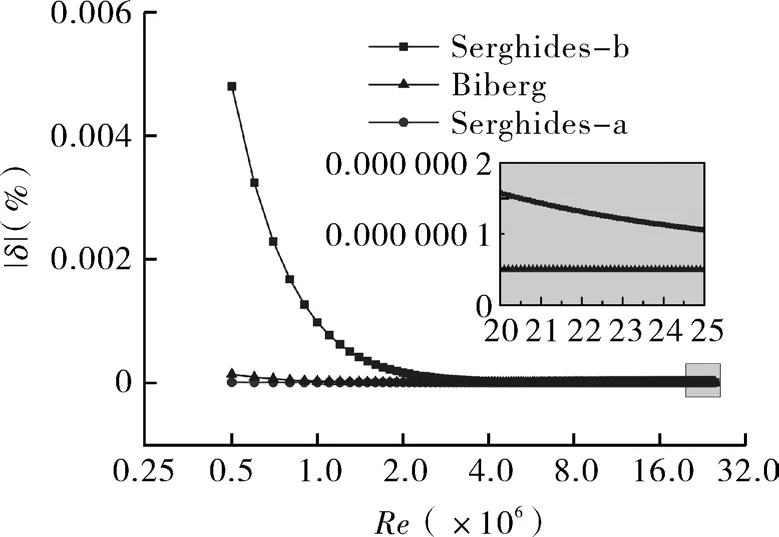
图6 ε/D=1/2 800误差随Re的变化Fig.6 Variation of error with Re for ε/D=1/2 800

图7 ε/D=1/3 200误差随Re的变化Fig.7 Variation of error with Re for ε/D=1/3 200

3 结论

（1）Colebrook-White公式适用长输供热管网计算。在常见的参数范围内，长输供热管网的雷诺数分布在6×105～2.456×107之间，属于Colebrook-White公式的适用范围。

（2）雷诺数对摩擦阻力系数的影响很大。在本文选择的20个近似式中，在雷诺数较小时，有部分近似式误差较大。管径和管道内壁当量粗糙度对摩擦阻力系数的影响相对较小。

（3）Biberg公式、Serghides-a适合作为长输供热管网的水力计算。在供回水温度为20～130 ℃、压力为0.5～2.5 MPa、管径为DN1 200～DN1 600，即1/3 200≤ε/D≤1/2 400的长输供热管网常见运行参数范围内，Biberg公式和Serghides-a的计算稳定性和精度极高，解决了Colebrook-White公式的隐式计算问题，适合作为长输供热管网的水力计算。