磁控溅射薄膜生长的模拟方法

王晓倩，赵晋，刘建勇

磁控溅射薄膜生长的模拟方法

王晓倩，赵晋，刘建勇

（天津工业大学 纺织科学与工程学院，天津 300387）

磁控溅射技术制备的薄膜膜层均匀，内部无气孔，密度高，与衬底的附着性良好，薄膜质量高，被广泛应用于科学研究和工业生产中，且适合应用计算机模拟来研究溅射过程和溅射结果，这样既可以检验模拟的准确性，又可以对实验现象的内在意义进行挖掘，为后续实验提供参考信息。在介绍磁控溅射薄膜生长常用模拟方法原理的基础上，详细讨论了第一性原理（First-principles calculations）、分子动力学（Molecular dynamics，MD）和蒙特卡洛（Monte Carlo，MC）等3种方法的适用条件和模拟结果，从3种方法适合解决的问题、相互之间的区别等方面，对国内外最新的研究进展进行总结与分析。发现3种方法在精确度和计算量上依次递减，在可模拟的时间和空间尺度上依次递增，在模拟对象上，第一性原理方法由于其高度的精确性被广泛应用于对薄膜本身的性质或对粒子间的运动等方面，且模拟结果可以是具体数值，从而对实验进行更加精确的预测和指导，分子动力学方法多用于模拟薄膜生长过程和原子间行为等方面，蒙特卡洛方法相较于前两者，用途更加广泛，可模拟的对象除了薄膜本身，也可以对电磁场等进行模拟。最后，对磁控溅射薄膜生长模拟未来的研究方向进行了展望。

磁控溅射；第一性原理方法；分子动力学方法；蒙特卡洛方法；数值模拟；薄膜

磁控溅射技术兴起于20世纪70年代，因其具有镀膜面积大，污染小，沉积快速，可制备多种类型的薄膜等优点，从而深受广大科研工作者和工业生产人员的欢迎。进入21世纪后，磁控溅射技术制备的薄膜由于其优异的物理和化学性能，很快在各个研究领域得到重视，其中也包括计算材料学。

为了提高溅射薄膜的质量和种类，得到科学研究中需要的特殊性能，对于薄膜生长微观层面的研究非常必要。薄膜生长是一个复杂的非平衡态过程，以实验来研究磁控溅射薄膜生长的原理及过程需要耗费大量的时间和实验材料，而且难以追踪原子的运动路径。计算机模拟作为研究凝聚态物理和材料科学的理论方法之一，是科学研究的重要工具，不仅可以降低研究成本和时间，还可以观察薄膜沉积的过程，追踪原子的运动路径，从原子角度研究薄膜生长的过程以及各因素对薄膜生长的影响，对薄膜生长的预测更加准确，对科学研究具有重要的指导意义。

磁控溅射过程中可进行模拟研究的对象包括薄膜沉积的过程及结果、电磁场和等离子体分布等。总结了近5年国内外在磁控溅射技术的模拟研究方面发表的文献情况（见图1），发现主要的研究集中在薄膜沉积的过程或结果的模拟，而与电磁场和等离子体相关的模拟在数量上相差不大，约占11%，而其他诸如靶材刻蚀、气体放电、流场相关的模拟近几年则研究得越来越少，关于薄膜沉积的模拟是近几年的主要研究趋势。

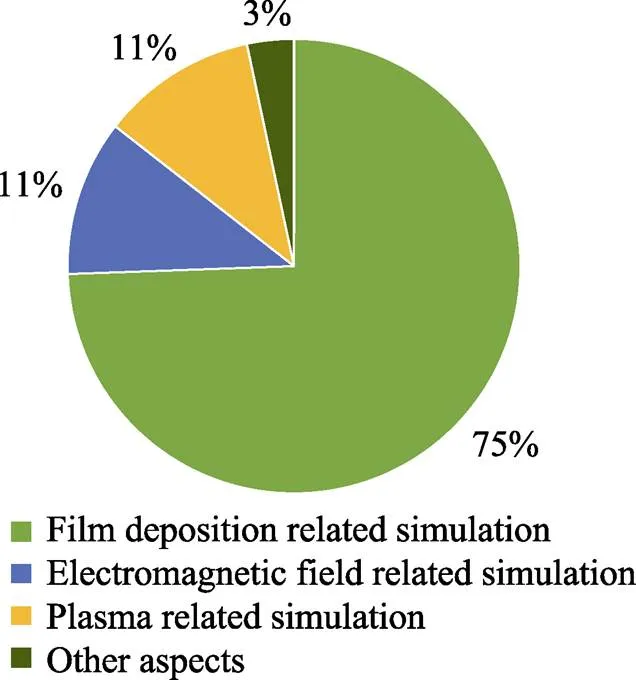
图1 近5年磁控溅射模拟对象的研究占比

1 模拟方法及其应用

随着计算能力和计算方法的不断发展，再加上高度创新的算法和理论模型，计算材料学已经从解释材料特性的工具发展成为性能预测，甚至结构和成分设计的重要方法。目前的模拟方法可以涵盖不同的时空尺度范围，在研究磁控溅射薄膜生长中应用较为广泛的主要有以下3种：第一性原理方法、分子动力学（MD）方法和蒙特卡洛（MC）方法。其中，第一性原理方法和分子动力学方法属于确定性方法，蒙特卡洛方法属于非确定性方法。

1.1 第一性原理方法

第一性原理计算[1]（First-principles calculations）指只以基本常数和研究对象的化学组成为基础求解薛定谔方程，进而对体系基态的电子结构进行计算的一种方法[2]，其理论基础为波恩-奥本海默（Born- Oppenheimer）绝热近似[3]和Hartree-Fock近似[4-5]。在此基础之上，霍恩伯格（Hobenberg）、科恩（Kohn）和沈吕九（Sham）等为更好求解多粒子体系Schrödinger方程，从而更精确地计算研究物质的电子结构和预测物质性质，提出了密度泛函理论（DFT），被广泛应用于凝聚态物理和材料科学领域中。

密度泛函理论（DFT）是一个计算固体材料、分子等电子结构和总能量的有力工具，该理论指出每个多粒子体系的电荷密度都有一个对应的外势场，体系的基态电荷密度决定了基态电子结构性质。随着密度泛函理论的不断发展，以霍恩伯格-科恩（Hohenberg- Kohn）定理[6]和Kohn-Sham定理[7]为基础，提出了交换关联泛函、局域密度近似（LDA）[8]、广义梯度近似（DDA）[9-10]、赝势方法[11]等理论，从不同方面完善了第一性原理方法。

构建模型的步骤：首先参考Born-Oppenheimer绝热近似[3]，将多粒子问题转化为多电子问题；其次再以Hartree-Fock近似[4-5]或密度泛函理论[12]为基础，把多电子问题转化为单电子问题；最后求解单电子方程，从而计算出想要的结果，其中包括赝势的假设和交换关联密度泛函的选取[13-14]。

目前第一性原理方法在磁控溅射薄膜生长上的用途主要有以下几方面。

1）从微观层面模拟粒子间的运动，预测薄膜性能，寻找最优方案，对实验进行指导，减少实验次数。国际上对于第一性原理在磁控溅射薄膜模拟方面的应用可以追溯到2001年，Gall.D等利用基于密度泛函理论的第一性原理计算方法模拟ScN（氮化钪）的能带结构，得出ScN是一种半导体而不是半金属的结论，实验结果与模拟结果一致[15]。该作者还计算了ScN和TiN（氮化钛）的能带结构[16]，用于模拟Sc1–xTiN中自由载流子对电场和磁场的响应，并结合测得的温度与电阻率的关系确定了低温载流子弛豫时间，得到的结果与光学测量结果吻合。在此之前，密度泛函理论因为具有各种局限性，更多地被当作对研究结果的辅助性论证。现在密度泛函理论除了可作为辅助验证实验结果的手段，还可作为从理论方面解释实验结果的有力工具。如Viktor Šroba等[17]采用第一性原理方法预测出在硼亚晶格中含有大量硼空位的六角α-TaB2相具有高稳定性的结果，并且进行了实验验证，实验结果与预测结果相吻合。国内早在2006年李喜峰[18]为揭示载流子的产生机理，分析掺杂原子对导带底部态密度的影响，以DFT为基础进行第一性原理计算，得到W和Mo掺杂的In2O3体系的能带结构和电子结构，采用GGA计算结果与LDA近似计算结果相一致，都为1.3 eV，而实验所得的禁带宽度为3.75 eV，实验结果与模拟结果不同表明，选择不同的近似方法无法修正模拟带偏低现象，但模拟结果仍可用于分析In2O3电子结构。近些年对于密度泛函理论的应用也集中于对薄膜本身的性能或对薄膜进行粒子层面的模拟。赵艳芳[19]利用密度泛函理论对ZnO薄膜进行模拟，分析了ZnO的n型掺杂和p型掺杂晶体结构、光电性质和掺杂机制，从理论上探究ZnO太阳能电池实现的可能性，在研究中分别计算了纯ZnO、In0.0625Zn0.9375O（In掺ZnO超晶胞）和Al0.0625Zn0.9375（Al掺ZnO的超晶胞）的晶格参数和能带结构，计算得出ZnO的带隙值为0.714 eV，与其他人的计算结果相符，虽然低于实验结果的3.37 eV，但并不影响此研究中的对比分析。

2）从宏观层面模拟薄膜本身的各项性能指标，如电导率、折射率、透射率等。马群超等[20]采用第一性原理方法计算了TiN的电子态密度，结合相关实验测试结果，说明了TiN能在集成电路充当电极及作为热反射涂层应用于低辐射薄膜的原因，又根据计算结果，结合经典的色散模型和已有的关于TiN色散模型的研究，提出了适合于TiN的Drude-3Lorentz色散模型。高伟[2]通过第一性原理方法模拟计算了本征ZnO，Al掺ZnO，Eu掺ZnO以及Al-Eu共掺ZnO的能带结构、态密度、反射率和透射率等，其中本征ZnO超晶胞在经过几何优化后，其结果与其他研究者计算的结果相一致，本征ZnO的带隙计算值为0.734 eV，与其他研究者的计算结果相一致。虽然与实验结果相差较大，但不会对定性分析体系的基本性质产生影响，最终分析得出Al、Eu掺杂过后ZnO的晶格常数及体积都有所增大，费米能级进入导带，体系呈现n型导电，带隙减小的结论。

3）从薄膜微观结构的层面，模拟引入某种物质，或者改变条件后会对薄膜造成何种影响，进而研究对薄膜性能的影响，通常采用模拟与实验相结合的方式研究。Aleksandra Szkudlarek[21]等研究了Cr掺杂对CuO和Cr掺杂CuO薄膜电子结构的影响，利用密度泛函理论计算了p型CuO和p型Cr掺杂CuO的电子结构，计算结果表明，在此工艺下，Cr缺陷形成的能量很低，结合实验分析表明，Cr掺杂可以有效地将电子贡献给导带，从而减少p型半导体中的空穴数量。徐文超[22]使用第一性原理方法，研究了改变衬底结构对Mn0.625Ga0.375薄膜晶格常数和磁各向异性能等的影响，定性分析了薄膜的性能变化，再结合实验加以论证，结果表明，随着衬底晶格常数的增大，晶胞体积逐渐增大，MnGa薄膜的值逐渐减小，/值线性降低，磁化强势度逐渐减小。由于计算只是模拟了MnGa薄膜在(001)方向上的生长，所以与实验中薄膜生长方向并不完全符合，后续还需优化溅射仪的真空条件，才能使计算结果与实验结果结合得更加紧密。

1.2 分子动力学方法

1957年分子动力学（MD）首先被Alder应用于硬球系统研究固液相变问题，之后应用于液态氩和水分子的模拟。1980年之后，随着控温方法的丰富，众多分子计算理论被提出，软件开发不断进步。目前分子动力学模拟在凝聚态物理、材料科学等领域都有着广泛的应用[23]，其原理是在假定原子的运动由牛顿方程决定，由此计算原子间的作用力，建立运动方程，并进行数值求解，确定原子的运动轨迹，进而计算体系的结构和性质，这是对平均时间的动态计算过程[23-24]。通常为了简化计算，引入了DFT，釆用经验势函数或者半经验势函数进行计算模拟[25-26]。

由于分子动力学方法的使用前提是假定所有原子运动遵循牛顿方程，并且求解牛顿运动方程，因此需要知道体系中粒子之间的相互作用。体系中粒子之间的相互作用由势能函数决定，所以分子动力学模拟的准确程度由势能函数的精确性决定。如果势能函数过于复杂，则会增加计算机的运算量，导致运算速率下降，因此势能函数的选择至关重要。目前常用的势能函数有对势中的LJ势和Morse势[27-28]，多体势中的EAM势[29]和AIREBO势[30]等。

目前分子动力学在磁控溅射薄膜生长上的应用主要集中在以下几方面。

1）对薄膜原子生长过程的模拟。Xuegang Zhu[31]等通过分子动力学模拟研究直流磁控溅射中以Be（0001）为基底，溅射Be原子的入射能量和入射角对Be薄膜生长形貌演化的影响，分析得出结论，当入射能量在1～20 eV之间时，表面粗糙度随着入射能量的增加而减小；当入射能量大于15 eV时，在表面下会形成间隙原子缺陷，随着入射角的减小，表面粗糙度减小且晶体比率增加，大的入射能量和垂直入射原子有助于形成均匀的晶体膜和光滑表面。Pascal Brault[32]等对Pd和PdO纳米团簇的生长进行了分子动力学模拟，并结合实验进行分析，在无氧的情况下形成Pd团簇时，团簇过程在模拟时间25 ns内完成，在溅射气体中添加O2时，团簇过程不完整且很小，且PdO和Pd2O之类的分子很多，而且溅射气体中的氧气有55%的分子没有反应，这导致PdO团簇生长的动力学比Pd团簇生长的动力学慢得多。Jean-Gabriel Mattei[33]通过分子动力学模拟，将生长过程分解为基本步骤，确定了Au/Pt与Pd生长动力学之间的根本区别：Au/Pt电子排列倾向于形成二聚核，而不是较大尺寸的团簇，从而大大减慢了其生长速度，相比之下，Pd的电子结构使其能够快速生长，因此较大的Pd颗粒形成的速度相当快，并通过飞行中的修饰和聚结的方式结合成小的Au和Pt团簇。Xuegang Zhu和Xinlu Cheng[34]通过分子动力学模拟，研究了Be膜在含有不同GBs（晶界）基底上的生长情况，研究表明，随着Be晶粒的取向差角从0°增加到30°，晶体比降低，位错密度增加，当入射能量低时，低角度GBs演化为非晶结构；当入射能量低于5 eV时，随着入射能量的增加，GBs的宽度减小，内部空隙缺陷的数量和表面粗糙度降低，大约5 eV的入射能量足以形成优质的Be膜。

2）模拟原子之间的行为。Zhixiang Liu[35]等基于分子动力学和第一性原理，建立并分析了Si/ZnO和Si在ZnO模型中的扩散，结果表明薄膜经热处理后一定量的Si原子（以间隙态）与O原子相互作用，而SiO32–（硅酸盐）是由于Si原子与Zn—O键相关的O原子之间的反应而形成的，且Si—O键很强，使靠近Si原子的Zn—O化学键断裂，在ZnO中留下氧空位，因此，Si与ZnO之间的界面相互作用取决于ZnO薄膜中的氧含量，有限的氧可以增加Si/ZnO界面相互作用的宽度，并因Zn—O键合使ZnO薄膜中的氧原子发生空位，这与实验结果相一致。Myung Eun Suk[36]采用非平衡分子动力学方法研究了薄膜/基底界面原子无序的影响，结果表明，通过直流溅射制备的薄膜具有比蒸发的电子束制备的薄膜更粗糙的表面和更高的热边界电阻，随着原子互混层厚度的增加，热边界电阻也增加，与实验所得结果相一致。Guo Zhu[37]等采用分子动力学方法研究了磁控溅射过程中温度对Si(001)上Cu薄膜生长的影响（见图2），图2a—c为薄膜横截面中铜和硅原子的分布，图2d—f显示了薄膜横断面的微观结构，图2中青色表示面心立方结构，黄色表示体心立方结构，绿色表示密排六方结构，红色表示金刚石结构，蓝色表示无定形结构，黑色线表示界面混合的宽度，红线代表初始基材表面。由模拟结果可知，非晶态结构出现在薄膜-基底界面的底部，并且非晶态结构的比例随着温度的升高而增加。

图2 在（a）300、（b）600和（c）900 K时垂直于膜表面的横截面中的铜原子和硅原子的分布以及（d）300、（e）600和（f）900 K时垂直于膜表面的横截面中的晶体微观结构

1.3 蒙特卡洛方法

蒙特卡洛方法（MC）最早出现在20世纪40年代末和50年代，是以概率为基础的方法，也是统计模拟方法的别称。关于蒙特卡洛方法模拟薄膜生长，由最早的扩散聚集模型（DLA）[38]，以及后来改进提出的TSK模型[39]、DDA模型[40]等，成功模拟了薄膜生长的过程和影响因素，且得到了实验证实。

蒙特卡洛方法模拟薄膜生长的思想是，首先建立一个随机模型，对粒子所有运动规定概率，然后用随机抽样法来确定每个原子的运动，最后统计求解[23]。计算过程中不需要求解原子的运动方程，因此计算量较小，适合模拟复杂随机过程。在研究“薄膜生长”这一典型的非平衡随机的原子聚集过程的问题上[41]，它集中表现了原子在表面的沉积、吸附、扩散、成核、生长等一系列复杂过程。蒙特卡洛方法为这样复杂的过程提供了一个有效、方便、快捷的模拟手段[23,42]，因此具有更加广阔的应用。

蒙特卡洛方法的适用范围主要有以下几方面。

1）模拟薄膜生长过程，研究实验条件对薄膜产生的影响。宋超群[43]利用蒙特卡洛方法在有缺陷的基底上构建三维模型，模拟Cu(100)面的薄膜生长过程，研究基底温度和粒子在基材沉积时的能量等因素对薄膜生长的影响，模拟结果表明，随着基底温度的增加，粒子由分散生长转变为凝聚生长，而岛的平均尺寸也逐渐变大，数目减少，但仍存在分散粒子，而粒子能量的增加对其生长过程的影响与基底温度的影响一样，模拟结果与实验结果相符合；郝国防[44]、王亭力[25]、李庆成[45]等分别运用蒙特卡洛方法对薄膜生长进行了模拟，探究了温度对薄膜生长的影响。王亭力采用蒙特卡洛方法模拟了Ag薄膜的生长过程，并且研究了温度对薄膜的岛的影响，由图3[25]可得出结论，在磁控溅射沉积薄膜的过程中，靶材粒子先形成核，核逐渐长大形成岛，岛之间相互连接形成薄膜；通过对不同温度下沉积相同原子数的模拟间进行比较，可以看出溅射温度越高，沉积粒子形成的岛尺寸越大，岛的数量和单个原子的数量减少。

2）模拟粒子的运动。Martin Evrard[46]等模拟了薄膜沉积过程，模拟了不同压强下不同靶材溅射薄膜的厚度，并与实验进行比较，得出结论，元素越轻，局部厚度的模拟越好；压强越低，预测越准确。R. Tonneau[47]等采用三维直接模拟蒙特卡洛（DSMC）技术模拟了溅射材料在真空室中的输运，模拟了3种压力下阴影和非阴影的表面上，动态和静态溅射铬、银和钽的沉积厚度，再将模拟值和实验值进行了比较，结果表明，无论表面、沉积的材料、压力和运动类型如何，都能准确模拟各个条件下的薄膜厚度。除此之外，蒙特卡洛方法还可用于磁控溅射过程中对电磁场的模拟[48]，计算入射粒子能量和角分布[49-50]等。

在蒙特卡洛方法的基础之上衍生出很多方法，如将分子动力学与蒙特卡洛方法相结合的分子动力学蒙特卡洛方法[47]、PIC/MCC方法[51-52]等，这些方法使计算机的模拟更加准确。

2 各种模拟方法的选择和适用性

通过上述分析可以看出，不同的模拟方法各有所长，在实际应用中，应该根据研究的目的、材料、条件等因素，参照图4选择不同的模拟方法。

由图4可以看出，每种方法各自的模拟尺度不同，模拟时间尺度越长，空间尺度越大，模拟结果的精确性越低，相对来说模拟所需的时间和计算量则越少，所以应根据具体研究的问题选择合适的计算方法，也可以将不同的方法结合起来更好地对模拟体系进行研究。第一性原理、分子动力学方法和蒙特卡洛方法是使用最为广泛的3种原子尺度模拟方法，是帮助理解材料科学中发生的基本物理过程的重要理论技术，它们提供了计算技术或工具来描述原子与电子之间的相互作用，计算电荷分布和电荷转移，获得电子基态及其本征值，监视原子运动并找出轨迹，最后从动力学或热力学的角度收集材料在原子水平上的物理和化学性质的所有数据或信息。根据这些基本数据或信息，可以更好地了解材料的基本物理和化学特性，从而找到修改和设计材料的方法。

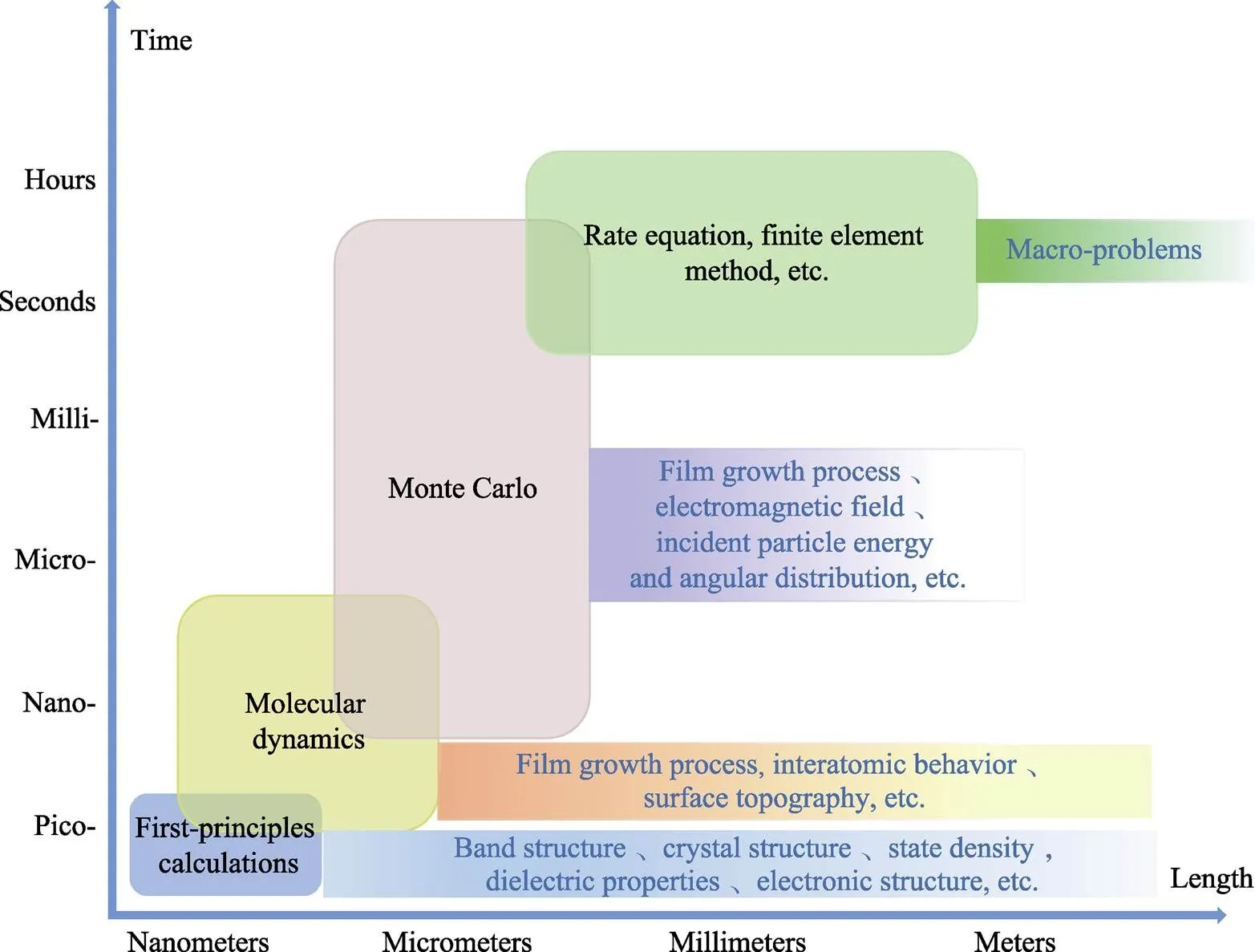
图4 各种模拟方法的适用性

粗略地统计了近5年应用3种主要模拟方法发表论文数量情况，见图5。由图5可以看出，由于近几年的研究越来越偏向于从微观层面模拟薄膜的各项性能，解释实验原理，因此对于第一性原理的应用较多。

除了磁控溅射之外，制备薄膜的方法还有化学气相沉积、原子层沉积法、溶胶-凝胶法、自组装和电化学沉积等，在模拟薄膜生长过程以及薄膜性能上，多用第一性原理方法[53]和分子动力学法[54-57]，蒙特卡洛方法使用得较少[58]。根据模拟对象的不同，可选用其他方法，如有限时域差分法(FDTD)[59]、耗散粒子动力学模拟方法[60-61]、流体力学方法（CFD）[62-63]等。

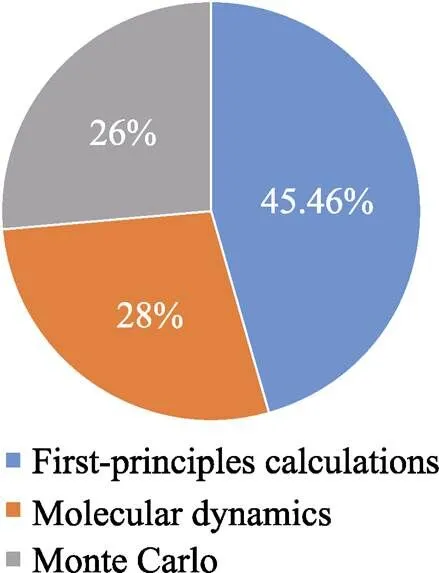
图5 近5年相关论文占比

3 结论

磁控溅射技术可应用于制备纳米级别的薄膜，且成膜均匀，具有良好的膜基结合力、光学性能、电学性能，适合进行微观层面的模拟。适合模拟小体系且准确性最高的第一性原理方法被广泛应用于模拟磁控溅射薄膜的原子及电子行为或薄膜性能。

此外，在磁控溅射薄膜沉积的过程中，原子的运动轨迹和原子间行为也是被广泛研究的对象，分子动力学方法可以较为精确地模拟这个过程，且计算量比第一性原理方法小。

除了以上2种方法，蒙特卡洛方法最早应用于磁控溅射薄膜的模拟，虽然准确程度不及前2种方法，但是除了可预测薄膜性能和原子、电子行为外，还可以针对磁控溅射过程中的电磁场分布、等离子体分布、磁控管放电进行模拟，用途更加广泛。

将磁控溅射技术与计算机模拟相结合已成为目前的研究趋势，在具体研究中可以根据研究的对象，模拟所需时间长短，要求的精确性和模拟的尺度来选择合适的模拟方法。目前在模拟计算中存在一些问题，例如模拟数值不准确，模拟条件多为理想状态，基底单一等问题。在未来的研究中，应更新算法，提出新的更适合研究磁控溅射薄膜生长的模拟方法，或者在已有方法基础上不断改进，以提高计算的精度和尺度，缩减计算时间和计算量，不断探究在缺陷基底甚至曲面和柔性基底上的模拟，以适应实际实验的需要。

[1] SEGALL M D, LINDAN P J D, PROBERT M J, et al. First-Principles Simulation: Ideas, Illustrations and the CASTEP Code[J]. Journal of Physics: Condensed Matter, 2002, 14(11): 2717-2744.

[2] 高伟. Al-Eu共掺ZnO薄膜的制备及其第一性原理研究[D]. 镇江: 江苏大学, 2019: 10-28.

GAO Wei. Preparation and First Principle Study of Al-Eu Codoped ZnO Thin Films[D]. Zhenjiang: Jiangsu Univ­ersity, 2019: 10-28.

[3] BORN M, HUANG Kun, LAX M. Dynamical Theory of Crystal Lattices[J]. American Journal of Physics, 1955, 23(7): 474.

[4] HARTREE D R. The Wave Mechanics of an Atom with a Non-Coulomb Central Field. Part I. Theory and Meth­ods[J]. Mathematical Proceedings of the Cambridge Phi­losophical Society, 1928, 24(1): 89-110.

[5] FOCK V. Näherungsmethode Zur Lösung des Quanten­mechanischen Mehrkörperproblems[J]. Zeitschrift Für Physik, 1930, 61(1/2): 126-148.

[6] WU Xiao-jun, YANG Jin-long, HOU J G, et al. Hydrogen Adsorption on Zigzag (8, 0) Boron Nitride Nanotubes[J]. The Journal of Chemical Physics, 2004, 121(17): 8481-8485.

[7] WU Xiao-jun, YANG Jin-long, HOU J G, et al. Deform­ation-Induced Site Selectivity for Hydrogen Adsorption on Boron Nitride Nanotubes[J]. Physical Review B, 2004, 69(15): 153411.

[8] KOHN W, SHAM L J. Self-Consistent Equations Include­ing Exchange and Correlation Effects[J]. Physical Review, 1965, 140(4A): A1133-A1138.

[9] PERDEW J P, CHEVARY J A, VOSKO S H, et al. Atoms, Molecules, Solids, and Surfaces: Applications of the Gen­eralized Gradient Approximation for Exchange and Corr­elation[J]. Physical Review B, Condensed Matter, 1992, 46(11): 6671-6687.

[10] HAMMER B, HANSEN L B, NØRSKOV J K. Improved Adsorption Energetics within Density-Functional Theory Using Revised Perdew-Burke-Ernzerhof Functionals[J]. Physical Review B, 1999, 59(11): 7413-7421.

[11] HAMANN D R, SCHLÜTER M, CHIANG C. Norm- Conserving Pseudopotentials[J]. Physical Review Letters, 1979, 43(20): 1494-1497.

[12] 张跃, 谷景华, 尚家香. 计算材料学基础[M]. 北京: 北京航空航天大学出版社, 2007: 26-30.

ZHANG Yue, GU Jing-hua, SHANG Jia-xiang. Funda­mentals of Computational Materials[M]. Beijing: Beijing University of Aeronautics & Astronautics Press, 2007: 26-30.

[13] 熊娜娜. 氧化物半导体的性能表征与电子结构的研究[D]. 广州: 华南理工大学, 2013: 6-11.

XIONG Na-na. Characterization and Electronic Structure Analysis of Oxide Semiconductor[D]. Guangzhou: South China University of Technology, 2013: 6-11.

[14] 车兴森. 叠层太阳能电池吸收层Ge1–xC薄膜的制备与性能[D]. 西安: 西北工业大学, 2014: 25-28.

CHE Xing-sen. The Preparation and Properties of the Ge1–xCFilms Used for Absorber Layer of Tandem Solar Cell[D]. Xi'an: Northwestern Polytechnical University, 2014: 25-28.

[15] GALL D, STÄDELE M, JÄRRENDAHL K, et al. Elect­ronic Structure of ScN Determined Using Optical Spec­troscopy, Photoemission, Andab Initiocalculations[J]. Ph­ysical Review B, 2001, 63(12): 125119.

[16] GALL D, PETROV I, GREENE J E. Epitaxial Sc1–xTiN(001): Optical and Electronic Transport Properties[J]. Journal of Applied Physics, 2000, 89(1): 401-409.

[17] ŠROBA V, FIANTOK T, TRUCHLÝ M, et al. Structure Evolution and Mechanical Properties of Hard Tantalum Diboride Films[J]. Journal of Vacuum Science & Techn­ology A, 2020, 38(3): 033408.

[18] 李喜峰. 新型透明导电氧化物薄膜的研究[D]. 上海: 复旦大学, 2006: 79-87.

LI Xi-feng. Study on New Transparent Conductive Oxide Films[D]. Shanghai: Fudan University, 2006: 79-87.

[19] 赵艳芳. 纳米ZnO薄膜掺杂改性及其在太阳能电池中的应用研究[D]. 镇江: 江苏大学, 2017: 17-35.

ZHAO Yan-fang. Doping Modification of Nano-ZnO Films and Its Application in Solar Cells[D]. Zhenjiang: Jiangsu University, 2017: 17-35.

[20] 马群超, 张水, 周强, 等. TiN薄膜光学性质与色散分析的第一性原理研究[J]. 材料科学与工艺, 2019, 27(3): 85-89.

MA Qun-chao, ZHANG Shui, ZHOU Qiang, et al. Study on Optical Properties and Dispersion Analysis of Titan­ium Nitride Films by First-Principle Theory[J]. Materials Science and Technology, 2019, 27(3): 85-89.

[21] SZKUDLAREK A, KOLLBEK K, KLEJNA S, et al. Electronic Sensitization of CuO Thin Films by Cr-Doping for Enhanced Gas Sensor Response at Low Detection Limit[J]. Materials Research Express, 2018, 5(12): 126406.

[22] 徐文超. 衬底对MnGa薄膜微结构和磁性能影响的研究[D]. 武汉: 华中科技大学, 2017: 9-16.

XU Wen-chao. Research on the Influence of Substrate on the Microstructure and Magnetic Properties of MnGa Thin Film[D]. Wuhan: Huazhong University of Science and Technology, 2017: 9-16.

[23] 朱永超. 金属石墨烯复合薄膜制备的分子动力学模拟研究[D]. 郑州: 郑州大学, 2019: 14-75.

ZHU Yong-chao. Molecular Dynamics Simulation Study on Preparation of Graphene-Metal Composite Films[D]. Zhengzhou: Zhengzhou University, 2019: 14-75.

[24] 吴笑天. 基于磁控溅射技术的典型零件复合加工方法研究[D]. 南京: 南京理工大学, 2011: 17-38.

WU Xiao-tian. Research on Compound Machining Met­hod of Typical Parts Based on Magnetron Sputtering Technology[D]. Nanjing: Nanjing University of Science and Technology, 2011: 17-38.

[25] 王亭力. 单原子及多原子薄膜生长的蒙特卡罗模型[D]. 大连: 大连理工大学, 2015: 2-44.

WANG Ting-li. Monte Carlo Model of Single Atom and Polyatom Thin Film Growth[D]. Dalian: Dalian University of Technology, 2015: 2-44.

[26] TAVAZZA F, NURMINEN L, LANDAU D P, et al. Hybrid Monte Carlo-Molecular Dynamics Algorithm for the Study of Islands and Step Edges on Semiconductor Surfaces: Application to Si/Si (001)[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2004, 70(3): 036701.

[27] MORSE P M. Diatomic Molecules According to the Wave Mechanics Ⅱ Vibrational Levels[J]. Physical Review, 1929, 34(1): 57-64.

[28] 陈强, 曹红红, 黄海波. 分子动力学中势函数研究[J]. 天津理工学院学报, 2004, 20(2): 101-105.

CHEN Qiang, CAO Hong-hong, HUANG Hai-bo. A Research on the Interatomic Potential in Molecular Dyn­amics (MD)[J]. Journal of Tianjin Institute of Technology, 2004, 20(2): 101-105.

[29] DAW M S, BASKES M I. Semiempirical, Quantum Mechanical Calculation of Hydrogen Embrittlement in Metals[J]. Physical Review Letters, 1983, 50(17): 1285-1288.

[30] BRENNER D W, SHENDEROVA O A, HARRISON J A, et al. A Second-Generation Reactive Empirical Bond Order (REBO) Potential Energy Expression for Hydroc­arbons[J]. Journal of Physics: Condensed Matter, 2002, 14(4): 783-802.

[31] ZHU Xue-gang, LU Yu-ping. Growth of Beryllium Thin Films on Beryllium (0001) Surface: Influence of Incident Energy and Incident Angle by Molecular Dynamics Sim­ulation[J]. Journal of Applied Physics, 2018, 124(17): 175304.

[32] BRAULT P, CHAMORRO-CORAL W, CHUON S, et al. Molecular Dynamics Simulations of Initial Pd and PdO Nanocluster Growth in a Magnetron Gas Aggregation Source[J]. Frontiers of Chemical Science and Engine­ering, 2019, 13(2): 324-329.

[33] MATTEI J G, GRAMMATIKOPOULOS P, ZHAO Jun- lei, et al. Gas-Phase Synthesis of Trimetallic Nanopart­icles[J]. Chemistry of Materials, 2019, 31(6): 2151-2163.

[34] ZHU Xue-gang, CHENG Xin-lu. Molecular Dynamics Study of Tilt Grain Boundary Evolution during the Gro­wth of Beryllium Thin Films[J]. Journal of Crystal Gro­wth, 2020, 531: 125366.

[35] LIU Zhi-xiang, TANG Yun-qing, LIAO Ning-bo, et al. Study on Interfacial Interaction between Si and ZnO[J]. Ceramics International, 2019, 45(17): 21894-21899.

[36] SUK M E, KIM Y Y. Influence of Deposition Techniques on the Thermal Boundary Resistance of Aluminum Thin- Films[J]. International Journal of Precision Engineering and Manufacturing, 2019, 20(8): 1435-1441.

[37] ZHU Guo, SUN Jiang-ping, ZHANG Li-bin, et al. Mole­cular Dynamics Simulation of Temperature Effects on Deposition of Cu Film on Si by Magnetron Sputtering[J]. Journal of Crystal Growth, 2018, 492: 60-66.

[38] WITTEN T A, SANDER L M. Diffusion-Limited Aggre­gation, a Kinetic Critical Phenomenon[J]. Physical Rev­iew Letters, 1981, 47(19): 1400-1403.

[39] ZHANG Z, LAGALLY M G. Atomistic Processes in the Early Stages of Thin-Film Growth[J]. Science, 1997, 276(5311): 377-383.

[40] JENSEN P, BARABÁSI A L, LARRALDE H, et al. Dep­osition, Diffusion, and Aggregation of Atoms on Surfaces: A Model for Nanostructure Growth[J]. Physical Review B, Condensed Matter, 1994, 50(20): 15316-15329.

[41] 冯兰胜, 过润秋, 张进成. GaN薄膜外延过程的动力学蒙特卡洛仿真[J]. 西安电子科技大学学报, 2016, 43(3): 167-171.

FENG Lan-sheng, GUO Run-qiu, ZHANG Jin-cheng. Kinetic Monte Carlo Simulation of GaN Epitaxy[J]. Journal of Xidian University, 2016, 43(3): 167-171.

[42] 戴传玮. 磁控溅射薄膜生长的计算机模拟研究[D]. 上海: 复旦大学, 2009: 2-64.

DAI Chuan-wei. Study on Computer Simulation of Magn­etron Sputtering Film Growth[D]. Shanghai: Fudan University, 2009: 2-64.

[43] 宋超群. 基底温度等因素对薄膜生长影响的Monte Carlo模拟研究[D]. 秦皇岛: 燕山大学, 2009: 8-49.

SONG Chao-qun. Study Effect of Substrate Temperature to Thin Film Growth by Monte Carlo Simulation[D]. Qinhuangdao: Yanshan University, 2009: 8-49.

[44] 郝国防. 用MC方法模拟PLD铁电体薄膜的生长过程[D]. 桂林: 广西师范大学, 2011: 11-46.

HAO Guo-fang. Using MC Simulate PLD Ferroelectric Thin Film Growth Proces[D]. Guilin: Guangxi Normal University, 2011: 11-46.

[45] 李庆成. 磁控溅射铜薄膜生长过程的蒙特卡罗模拟[D]. 合肥: 合肥工业大学, 2009: 22-50.

LI Qing-cheng. Monte Carlo Simulation for the Growth of Magnetron Sputtering Cu Films[D]. Hefei: Hefei University of Technology, 2009: 22-50.

[46] EVRARD M, BESNARD A, LUCAS S. Study of the Influence of the Pressure and Rotational Motion of 3D Substrates Processed by Magnetron Sputtering: A Com­parative Study between Monte Carlo Modelling and Exp­eriments[J]. Surface and Coatings Technology, 2019, 378: 125070.

[47] TONNEAU R, MOSKOVKIN P, PFLUG A, et al. TiOx­deposited by Magnetron Sputtering: A Joint Modelling and Experimental Study[J]. Journal of Physics D: Applied Physics, 2018, 51(19): 195202.

[48] 郭永棒. 直流磁控溅射中荷电粒子分布的模拟研究[D]. 沈阳: 东北大学, 2012: 28-65.

GUO Yong-bang. Simulation of Charged Particles Distri­b­ution in DC Magnetron Sputtering[D]. Shenyang: North­eastern University, 2012: 28-65.

[49] ABADIAS G, ANĞAY F, MAREUS R, et al. Texture and Stress Evolution in HfN Films Sputter-Deposited at Oblique Angles[J]. Coatings, 2019, 9(11): 712.

[50] OLIVEIRA J C, FERREIRA F, ANDERS A, et al. Redu­ced Atomic Shadowing in HiPIMS: Role of the Therm­alized Metal Ions[J]. Applied Surface Science, 2018, 433: 934-944.

[51] CUI Sui-han, WU Zhong-zhen, XIAO Shu, et al. Simula­tion Study on Plasma Discharge and Transport in Cylind­rical Cathode Controlled by Expanding Electromagnetic Field[J]. Acta Physica Sinica, 2019, 68(19): 195204.

[52] SCHERG-KURMES H, HAFEZ A, SIEMERS M, et al. Improvement of the Homogeneity of High Mobility In2O3: H Films by Sputtering through a Mesh Electrode Studied by Monte Carlo Simulation and Thin Film Anal­ysis[J]. Physica Status Solidi (a), 2016, 213(9): 2310-2316.

[53] 陈力. 化学气相沉积Nb/Re层状复合材料界面反应与性能研究[D]. 昆明: 昆明理工大学, 2019: 21-24.

CHEN Li. Study on Interfacial Reaction and Properties of Nb/Re Laminated Composites Deposited by Chemical Vapor Deposition[D]. Kunming: Kunming University of Science and Technology, 2019: 21-24.

[54] 向文军, 朱朝菊, 刘丹, 等. 分子动力学模拟研究两亲聚合物与疏水纳米粒子自组装核-壳结构[J]. 化工学报, 2019, 70(1): 345-354.

XIANG Wen-jun, ZHU Zhao-ju, LIU Dan, et al. Molec­ular Dynamics Simulations Core-Shell Self-Assembly from Amphiphilic Polymer and Hydrophobic Nanopa­rticle[J]. CIESC Journal, 2019, 70(1): 345-354.

[55] 陈昀钊. 印制电路镀铜添加剂调控铜沉积平整化的研究[D]. 成都: 电子科技大学, 2019: 11-18.

CHEN Yun-zhao. Investigation of Smooth Copper Depo­sition with Additive Regulation for Printed Circuit[D]. Chengdu: University of Electronic Science and Techn­ology of China, 2019: 11-18.

[56] 程东, 严立, 严志军. 薄膜沉积过程的分子动力学模拟[J]. 大连海事大学学报, 2004, 30(2): 82-85.

CHENG Dong, YAN Li, YAN Zhi-jun. Molecular Dynamics Simulations of Physical Vapor Deposition[J]. Journal of Dalian Maritime University, 2004, 30(2): 82-85.

[57] 杜涛. 水泥基材料的纳米改性机理研究[D]. 哈尔滨: 哈尔滨工业大学, 2019: 48-71.

DU Tao. Study on the Nano-Modification Mechanism of Cement-Based Materials[D]. Harbin: Harbin Institute of Technology, 2019: 48-71.

[58] 曹进军, 单彦广. 三维纳米液膜沉积结构的模拟研究[J]. 化学通报, 2018, 81(7): 641-645.

CAO Jin-jun, SHAN Yan-guang. Simulation on Three Dimensional Nanoscale Thin-Film Deposition[J]. Chem­istry, 2018, 81(7): 641-645.

[59] 杨开青, 刘越峰, 毛艳丽. 环己烷/水界面自组装纳米银膜及性能研究[J]. 光散射学报, 2017, 29(2): 114-118.

YANG Kai-qing, LIU Yue-feng, MAO Yan-li. The Prop­erties Researched Based on the Prepared Cyclohe­xane/ Water Interface Self-Assembly Nanometer Silver Film[J]. The Journal of Light Scattering, 2017, 29(2): 114-118.

[60] 郭浩, 宋先雨, 赵国林, 等. 双亲纳米颗粒在选择性溶剂中的自组装行为: 耗散粒子动力学模拟[J]. 化工学报, 2018, 69(11): 4887-4895.

GUO Hao, SONG Xian-yu, ZHAO Guo-lin, et al. Self- Assembly Behavior of Amphiphilic Nanoparticle in Sele­ctive Solvents: Dissipative Particle Dynamics Simul­ations[J]. CIESC Journal, 2018, 69(11): 4887-4895.

[61] 李达, 管洲, 王立权, 等. 图案化两亲性刚-柔嵌段共聚物薄膜的耗散粒子动力学模拟[J]. 功能高分子学报, 2018, 31(5): 446-453.

LI Da, GUAN Zhou, WANG Li-quan, et al. Dissipative Particle Dynamics Simulation of Patterns on Thin Film Formed by Amphiphilic Rod-Coil Block Copolymers[J]. Journal of Functional Polymers, 2018, 31(5): 446-453.

[62] 朱黎明. Co-Re化学气相沉积设备与控制系统设计[D]. 绵阳: 西南科技大学: 2019: 22-31.

ZHU Li-ming. Design of Co-Re Chemical Vapor Depos­ition Equipment and Control System[D]. Mianyang: Sout­h­west University of Science and Technology, 2019: 22-31.

[63] 周荣亚, 徐艳华, 张荣蓓. 化学气相沉积法制备碳化硅过程的三维数值模拟[J]. 工业加热, 2018, 47(6): 34-37.

ZHOU Rong-ya, XU Yan-hua, ZHANG Rong-bei. 3D Numerical Simulation of Chemical Vapor Deposition Proc­ess of Silicon Carbide[J]. Industrial Heating, 2018, 47(6): 34-37.

Simulation Method of Magnetron Sputtering Film Growth

,,

(School of Textile Science and Engineering, Tiangong University, Tianjin 300387, China)

The film prepared by magnetron sputtering technology is uniform and free from pores inside, with high density, good adhesion to the substrate and excellent quality and has been widely used in scientific research and industrial production. Such film is suitable for the simulation by computer to study sputtering process and sputtering results, which can not only check the accuracy of simulation, but also excavate the intrinsic meaning of experimental phenomena and provide reference information for subsequent experiments. Based on the introduction of the principles of the commonly used simulation methods for the growth of magnetron sputtering films, the applicable conditions and simulation results of the three methods, first-principles calculations, molecular dynamics (MD) and Monte Carlo (MC), were discussed in detail and the latest research progress at home and abroad was summarized and analyzed from the problems to be solved by the three methods and the differences between the three methods. It was found that the three methods were successively decreasing in accuracy and calculation amount, but increasing sequentially in the simulation time and space scales. For simulation object, first-principles calculations method is mostly used to simulate the properties of the film or the motion between particles due to high precision and the simulation results can be accurate to the value, so as to make more accurate predictions and guidance for the experiment. The molecular dynamics method is mostly used to simulate the film growth process and the behavior between atoms. Compared with the former two, the Monte Carlo method is more versatile and can simulate the film and the electromagnetic field. Finally, the future research direction of magnetron sputtering film growth simulation is forecasted.

magnetron sputtering; first-principles calculations; Molecular dynamics; Monte Carlo; numerical simulation; films

O484

A

1001-3660(2022)02-0156-09

10.16490/j.cnki.issn.1001-3660.2022.02.014

2020-09-02；

2021-07-12

2020-09-02；

2021-07-12

王晓倩（1995—），女, 硕士研究生,主要研究方向为纺织品功能整理。

WANG Xiao-qian (1995—), Female, Master, Research focus：textile functional finishing.

刘建勇（1964—），男，硕士，主要研究方向为生态纺织品加工技术和功能纺织品。

LIU Jian-yong (1964—), Male, Master, Research focus: ecological textile processing technology and functional textile research.

王晓倩, 赵晋, 刘建勇. 磁控溅射薄膜生长的模拟方法[J]. 表面技术, 2022, 51(2): 156-164.

WANG Xiao-qian, ZHAO Jin, LIU Jian-yong. Simulation Method of Magnetron Sputtering Film Growth[J]. Surface Technology, 2022, 51(2): 156-164.