常系数非齐次线性微分方程特解的新解法
2022-03-02方晓峰
张 辉,方晓峰,王 静
(火箭军工程大学 基础部,陕西 西安 710025)
0 引言
n阶常系数非齐次线性微分方程
y(n)+p1y(n-1)+p2y(n-2)+…+pn-1y′+pny=f(x)
(1)
通解的求解是高等数学中一个重要的知识点,也是难点问题之一。国内出版的大多数教材主要解决了f(x)在两种特定表达式情形下通解的计算问题。事实上,n阶非齐次线性微分方程(1)的通解等于对应齐次线性微分方程的通解与本身的一个特解之和,而对应的n阶常系数齐次线性微分方程的通解容易求得,因此关键是求解微分方程(1)的一个特解。大多数教材主要介绍了通过构造特解表达式(多个函数乘积)再利用待定系数法把特解求解出来的方法。事实上,在利用待定系数法求解过程中需要大量计算特解表达式的一阶导数、二阶导数、三阶导数直至n阶导数。一方面计算量较大,另一方面高阶导数的计算容易出错,带来了许多不便和困难。为了有效解决此类问题,本文研究了一种求微分方程(1)特解便捷有效的方法:待定多项式法。下面同样根据f(x)的表达式类型分两种情形讨论和研究。
1 f(x)=eλxPm(x)情形
已知m次多项式Pm(x)=a0xm+a1xm-1+…+am-1x+am(a0≠0),记n次多项式φ(r)=rn+p1rn-1+…+pn-1r+pn。利用指数函数与多项式乘积的导数仍为指数函数和多项式的乘积,教材[1]要求构造具有形如y*=xkeλxQm(x)的特解,其中Qm(x)为与Pm(x)次数相同的m次多项式b0xm+b1xm-1+…+bm-1x+bm(b0≠0),k按照λ不是特征方程φ(r)=0的根、是φ(r)=0的单根、是φ(r)=0的s重根,分别取0、1、s。事实上,在求特解y*过程中关键是确定Qm(x)表达式中m+1个系数b0,b1,…,bm-1,bm。教材[1]要求将y*=xkeλxQm(x)代入微分方程(1)中利用待定系数法求解出,计算量较大。如何便捷简单有效求出这m+1个系数?下面提出一种新的方法——待定多项式法求解。
记特解y*=eλxQ(x),其中Q(x)为一待定多项式,具体次数和系数待定。因为
y*′=Q′(x)eλx+λQ(x)eλx,
y*″=Q″(x)eλx+2λQ′(x)eλx+λ2Q(x)eλx,
…
将y*代入微分方程(1)中化简得
(2)
1)当λ不是特征方程φ(r)=0的根时,φ(λ)≠0。因为Pm(x)为m次多项式,则Q(x)也为m次多项式,取Q(x)=Qm(x),将其代入等式(2),通过比较多项式的系数就可以得到关于未知系数b0,b1,…,bm-1,bm的线性方程组,进而求得这m+1个系数并得到Qm(x)的表达式。
2)当λ是φ(r)=0的单根时,φ(λ)=0,φ′(λ)≠0,则Q′(x)为m次多项式,取Q(x)=xQm(x)=x(b0xm+b1xm-1+…+bm-1x+bm),将其代入等式(2)中可求得Qm(x)的系数b0,b1,…,bm-1,bm。
3)当λ是φ(r)=0的s(s≥2)重根时,φ(λ)=φ′(λ)=…=φ(s-1)(λ)=0,φ(s)(λ)≠0,则Q(s)(x)为m次多项式,取Q(x)=xsQm(x)=xs(b0xm+b1xm-1+…+bm-1x+bm),将其代入等式(2)中可求得Qm(x)的系数b0,b1,…,bm-1,bm。
以上3种情形得到了Qm(x)的表达式,进而可得Q(x)的表达式,最后再代入y*=eλxQ(x)即为微分方程(1)的一特解。通常把上述方法称为待定多项式法。此种方法的核心是求待定多项式Q(x)的表达式,其构造形式为Q(x)=xkQm(x),其中k按照λ不是φ(r)=0的根、是φ(r)=0的单根、是φ(r)=0的s重根分别取0、1、s,此时多项式Q(x)的次数分别为m、m+1、m+s。此时的关键是确定Qm(x)表达式中的m+1个系数。为了方便记住Q(x)的表达式,现总结出以下口诀:λ不是根幂(k)为0,是单根幂为1,是s重根幂为s。
若考察二阶常系数非齐次线性微分方程
y″+py′+qy=eλxPm(x),
(3)
则待定多项式Q(x)满足等式
Q″(x)+(2λ+p)Q′(x)+(λ2+pλ+q)Q(x)=Pm(x)。
(4)
表1给出了Pm(x)为不同类型多项式时待定多项式Q(x)的构造形式。

表1 待定多项式Q(x)的构造形式
特别地,若λ=0,则微分方程(3)的特解y*一定是一个多项式,也就是说待定多项式Q(x)即为特解y*。表2给出了3种情形下特解y*的构造形式。

表2 特解y*的构造形式
事实上,三阶常系数非齐次线性微分方程
y‴+hy″+py′+qy=eλxPm(x)
所对应的待定多项式Q(x)满足等式
Q‴(x)+(3λ+h)Q″(x)+(3λ2+2hλ+p)Q′(x)+(λ3+hλ2+pλ+q)Q(x)=Pm(x)。
2 f(x)=eλx(Pl(x)cos(ωx)+Pq(x)sin(ωx))情形
考虑n阶常系数非齐次线性微分方程
y(n)+p1y(n-1)+p2y(n-2)+…+pn-1y′+pny=eλx(Pl(x)cos(ωx)+Pq(x)sin(ωx)),
(5)
利用欧拉公式可以变形为
(6)
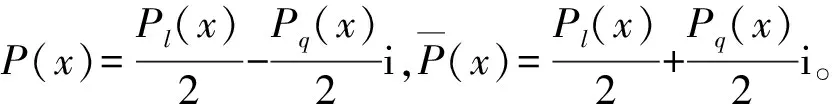
记
y(n)+p1y(n-1)+p2y(n-2)+…+pn-1y′+pny=P(x)e(λ+ωi)x,
(7)
(8)
y*=eλx((f(x)+g(x)i)eωxi+(f(x)-g(x)i)e-ωxi)=
eλx((f(x)+g(x)i)(cos(ωx)+isin(ωx))+(f(x)-g(x)i)(cos(ωx)-isin(ωx)))=
eλx(f(x)cos(ωx)+if(x)sin(ωx)+ig(x)cos(ωx)-g(x)sin(ωx)+
f(x)cos(ωx)-if(x)sin(ωx)-ig(x)cos(ωx)-g(x)sin(ωx))=
2eλx(f(x)cos(ωx)-g(x)sin(ωx))。
(9)
由上述分析可知,为了求微分方程(5)的特解y*,关键是确定Q(x)的实部函数f(x)和虚部函数g(x)的表达式。
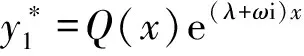
(10)
下面分3种情形分析。
1)当λ+ωi不是φ(r)=0的根时,φ(λ+ωi)≠0。因为P(x)为m次多项式,m=max{l,q},则Q(x)也为m次多项式,取Q(x)=Qm(x),其中Qm(x)为m次多项式,但不确定是Qm(x)实部多项式的次数还是Qm(x)虚部多项式的次数为m,也就是说Qm(x)实部多项式和虚部多项式中至少有一个次数为m。事实上,在实际问题求解过程中,记Qm(x)=fm(x)+gm(x)i,其中fm(x)和gm(x)都为次数不超过m的多项式。记
fm(x)=c0xm+c1xm-1+…+cm-1x+cm
和
gm(x)=d0xm+d1xm-1+…+dm-1x+dm,
则系数c0和d0至少有一个非零。将其代入等式(10)中,通过比较多项式的系数就可以得到关于未知系数c0,c1,…,cm-1,cm,d0,d1,…,dm-1,dm的线性方程组,进而求得这2m+2个系数。
2)当λ+ωi是φ(r)=0的单根时,φ(λ+ωi)=0,φ′(λ+ωi)≠0,则Q′(x)为m次多项式,取Q(x)=xQm(x),将其代入等式(10)中,可求得Qm(x)中的2m+2个系数。
3)当λ+ωi是φ(r)=0的s(s≥2)重根时,φ(λ+ωi)=φ′(λ+ωi)=…=φ(s-1)(λ+ωi)=0,φ(s)(λ+ωi)≠0,则Q(s)(x)为m次多项式,取Q(x)=xsQm(x),将其代入等式(10)中可求得Qm(x)中的2m+2个系数。
以上3种情形分别得到2m+2个系数c0,c1,…,cm-1,cm,d0,d1,…,dm-1,dm后便可确定多项式fm(x)和gm(x)表达式,从而可得Q(x)的表达式,又得到了f(x)和g(x)表达式,最后再代入式(9)即为微分方程(5)的一特解。通常把上述方法称为待定多项式法。
此种方法的核心是求f(x)和g(x)的表达式,其构造形式为f(x)=xkfm(x)和g(x)=xkgm(x),其中k按照λ+ωi不是φ(r)=0的根、是φ(r)=0的单根、是φ(r)=0的s重根分别取0、1、s。此时问题的关键是确定fm(x)表达式中的m+1个系数和gm(x)表达式中的m+1个系数,共有2m+2个系数。
特别地,考察二阶常系数非齐次线性微分方程
y″+py′+qy=eλx(Pl(x)cos(ωx)+Pq(x)sin(ωx)),
则待定多项式Q(x)=xk(fm(x)+gm(x)i)(其中m=max{l,q})满足等式
Q″(x)+(2(λ+ωi)+p)Q′(x)+((λ+ωi)2+p(λ+ωi)+q)Q(x)=P(x),
(11)
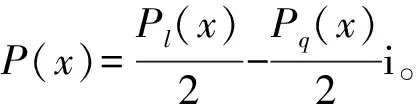
3 应用实例
例1求微分方程y″-5y′+6y=xe2x的通解。
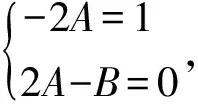
故所求的通解为
例2求微分方程y″+y=xcos(2x)的一个特解。
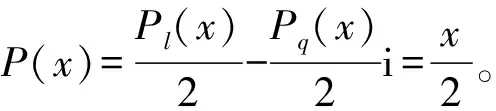
f1(x)=ax+b,g1(x)=cx+d,Q(x)=Q1(x)=f1(x)+g1(x)i=ax+b+(cx+d)i,
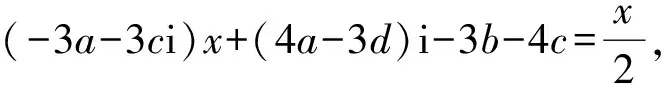
值得注意的是,Q(x)表达式中的f(x)是一次多项式,g(x)为零次多项式(常数),也就是说,多项式f(x)和g(x)的次数是不相同的。
以上两个例题都出自同济大学数学系编写的《高等数学》教材[1],通过计算比较可以发现,本文所提出的待定多项式法较为简单。事实上,待定多项式法最大的优势在于不再计算特解中涉及指数函数eλx的一阶导数和高阶导数,大大地减少了计算量,同时尽可能地避免出现计算错误。
需注意的是,对于常系数齐次或非齐次线性微分方程[3-8]通解的求解,可以利用MATLAB的函数dsolve完成。比如例1,在命令行窗口输入
dsolve(′D2y-5*Dy+6*y-x*exp(2*x)′,′x′)
点击run,运行结果为
C3*exp(3*x)-(x^2*exp(2*x))/2-exp(2*x)*(x + 1)+ C4*exp(2*x)
上述结果和例1所得结果是相同的,注意MATLAB的函数dsolve的功能是求解微分方程(包括线性微分方程)的通解,得到通解后便可以得到本身的一个特解。
