基于RJMCMC算法的Gamma分布形状参数多变点检测
2022-03-02程慧慧许淑月
程慧慧, 许淑月
(华北水利水电大学 数学与统计学院,河南 郑州 450046)
0 引言
所谓变点是指观测值在某一个位置或时间点发生了分布或数字特征的突然变化,这个位置或时间点称为变点。不考虑可能的变化点就进行统计分析很大可能会得到具有误导性的结果,因此变点问题的研究在金融学、医学、气象学和计算机科学等领域有着广泛的应用价值。众多学者对检测变点的方法进行了研究,如JAMES B J等[1]通过似然比方法检验多元正态分布变点是否存在;李拂晓等[2]使用Pearson卡方统计量的二元分割方法检验了多元Logistic回归模型中存在的变点;陈睿轩等[3]利用非参数极大似然方法对金融时间序列中的变点进行估计;CHERNOFF H等[4]应用贝叶斯方法检验正态分布中变点是否存在。
与经典统计学相比,贝叶斯方法不仅能对参数做出有效的估计,还使得变点检测变得更加简便,文献[5-9]都是基于贝叶斯方法解决多变点问题。尽管如此,贝叶斯变点问题中的计算仍是一大难点,尤其是在高维情形下与后验分布相关的一些积分很难用数值方法计算。对此,马尔可夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)算法作为一种重要的贝叶斯计算方法,将贝叶斯统计中复杂的计算简单化,在变点问题中得到广泛应用。如张晗等[10]在艾拉姆咖分布单变点模型中运用MCMC算法对变点位置做出了有效估计;石凯等[11]采用MCMC算法为多维混合分布数据的参数估计和识别提供了一种有效的解决途径。由于进行变点识别时贝叶斯后验计算会产生不同维数的多参数子空间,1995年GREEN P J[12]提出了可逆跳跃马尔可夫链蒙特卡洛(Reversible Jump Markov Chain Monte Carlo,简记为RJMCMC)算法。该采样器实现了抽样过程在不同维数的参数子空间之间跳跃,十分适用于多变点检测,如ZHAO X 等[13]在层次贝叶斯框架下利用RJMCMC算法识别极端事件序列中的多个突变状态;石永亮[14]利用RJMCMC算法对线性回归模型的异常点进行识别;刘鹤飞等[15]运用RJMCMC算法对隐状态个数未知的隐马尔可夫多元正态分布进行贝叶斯推断;李勇等[16]利用RJMCMC确定对隐状态个数未知的隐马尔可夫0-1分布进行贝叶斯推断;范元静等[17]利用RJMCMC算法确定泊松分布参数多变点模型中变点的个数,并在变点个数确定的基础上,结合MCMC方法进行参数估计。
Gamma分布经常出现在各种应用中,特别是在可靠性、生存分析和收入分配模型中。有关伽马分布形状参数ν的重要性也是毋庸置疑的,正如RAMANAYAKE A[18]所述:伽马分布是降低故障率、常数,还是增加故障率,都由ν-1的值所决定,并且形状参数ν在更新理论中也起着重要作用。关于Gamma分布参数变点的研究已有一些结果,如文献[19-22]考虑的是典型的伽马分布序列中的单变点问题;胡俊迎[23]在变点个数未知的情形下,利用RJMCMC算法对Gamma分布尺度参数进行多变点检测,并通过仿真模拟证明了在变点检测中RJMCMC算法显著优于S-N方法;但是有关Gamma分布的形状参数发生变化,以及形状参数和尺度参数同时发生变化的研究仍然较少。因此,在Gamma分布参数多变点模型中找到多个变点的数量及位置是一个重要且具有挑战性的统计问题。对比以往关于Gamma分布序列变点问题的研究,本文拟着重研究基于RJMCMC算法下的Gamma分布序列中形状参数的多变点检测,先利用算法确定变点个数,再通过MCMC算法估计变点位置和形状参数。
1 Gamma分布形状参数多变点模型
现有一组含有k个变点的观测值序列y1,y2,…,yn,yi独立且均服从Gamma分布。c1,c2,…,ck,将此观测值序列分成了k+1段,其中的第j段ycj-1+1,ycj-1+2,…,ycj,服从形状参数νj>0,尺度参数λj>0,j=1,2,…,k+1的Gamma分布。可将这个多变点模型表示为
(1)
为了方便,规定c0=0,ck+1=n。式(1)中,变点个数为k,变点位置分别在c1,c2,…,ck。现在先假定较为简单的一种情形:λj始终不发生变化,那么拟研究的变点模型(1)就是关于Gamma分布形状参数的多变点检测,需要估计的参数有2(k+1)个,分别是变点个数k;变点位置c1,c2,…,ck;形状参数ν1,ν2,…,νk+1。
2 推断原理及推断过程
2.1 贝叶斯估计原理
贝叶斯统计学是基于总体信息、样本信息、先验信息进行的统计推断。设参数θ的先验信息分布为π(θ),随机变量θ给定值时,总体的条件概率函数为p(x|θ)。样本X和参数θ的联合分布h(X,θ)=p(X|θ)π(θ),利用贝叶斯公式
(2)
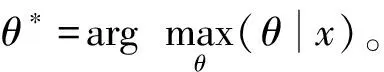
但是在实际问题中,上述后验密度分布(2)通常是比较复杂的未知形式,马尔可夫链蒙特卡洛(MCMC)方法可以解决这一难题,它以目标后验分布作为平稳分布的马尔可夫链生成随机数,代替从后验分布中直接抽取样本。
2.2 推断过程
在贝叶斯框架下的变点分析,需要确定各参数的先验分布,并推导出其后验分布。根据文献[12]可考虑各参数的先验分布。
1)变点个数k服从截断的泊松分布,
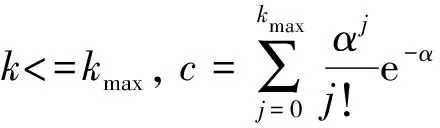
2)从离散的均匀分布{0,1,2,…,n}上产生2k+1个顺序统计量,c1,c2,…,ck作为其中的偶数阶统计量,
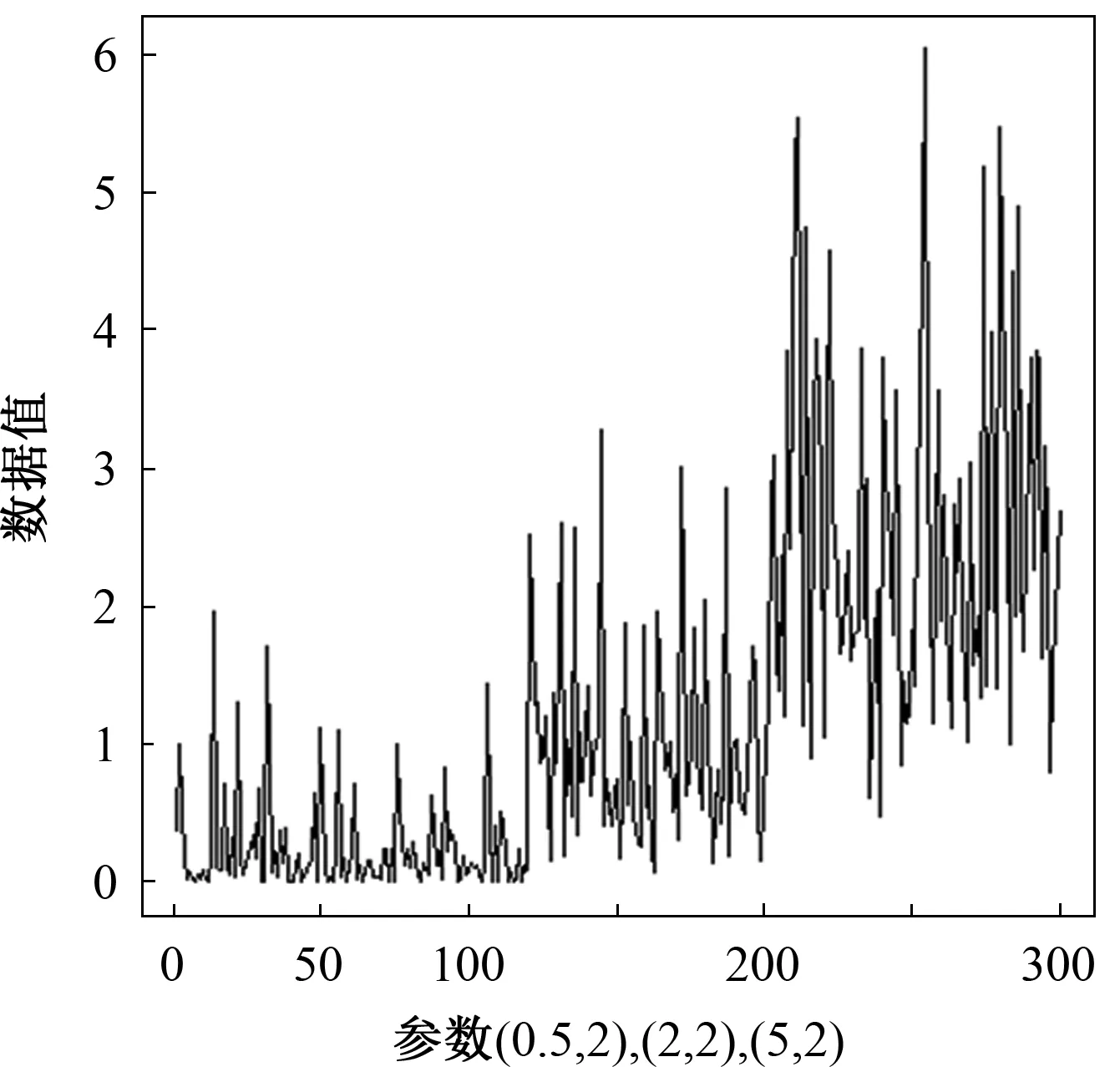
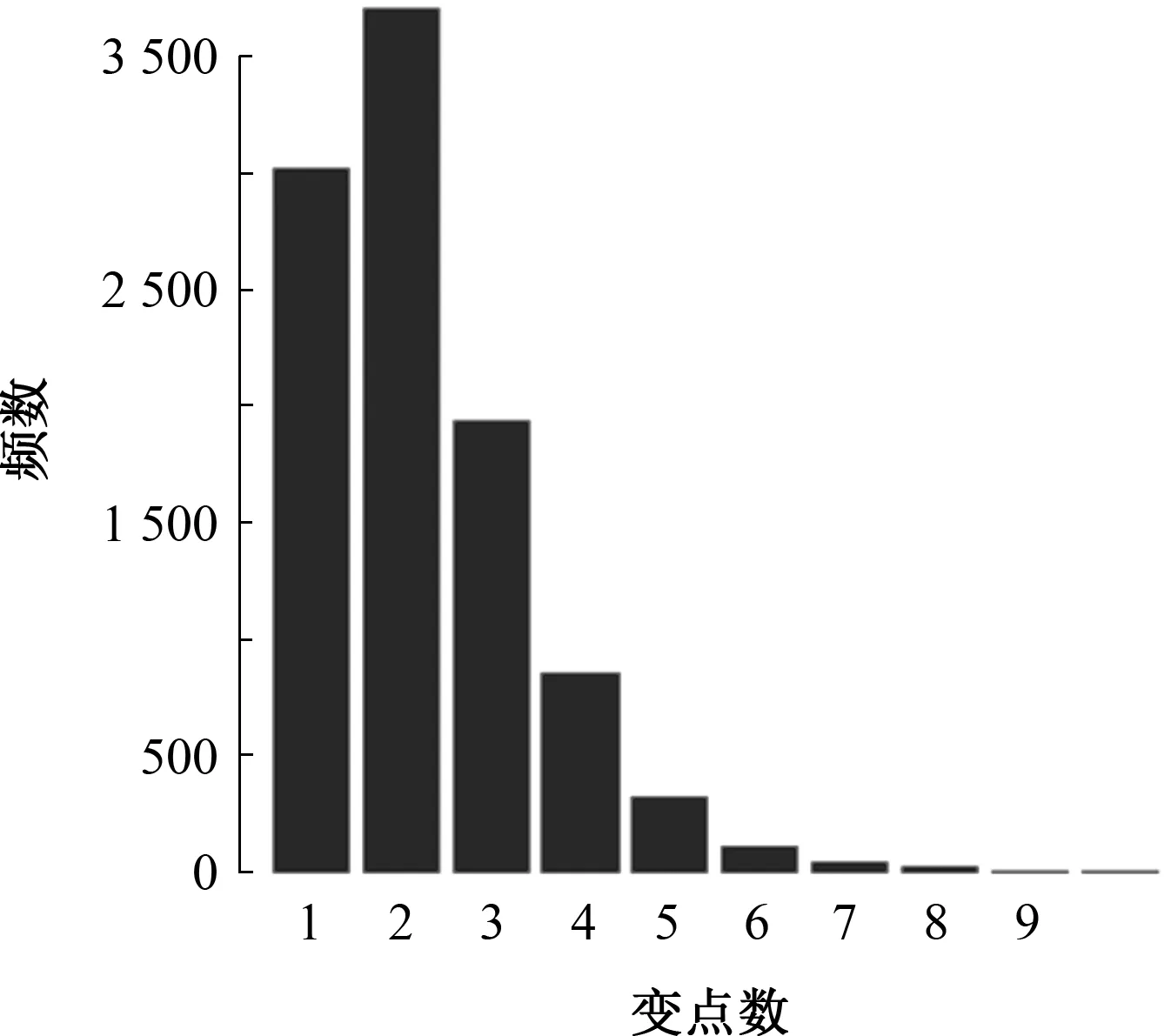
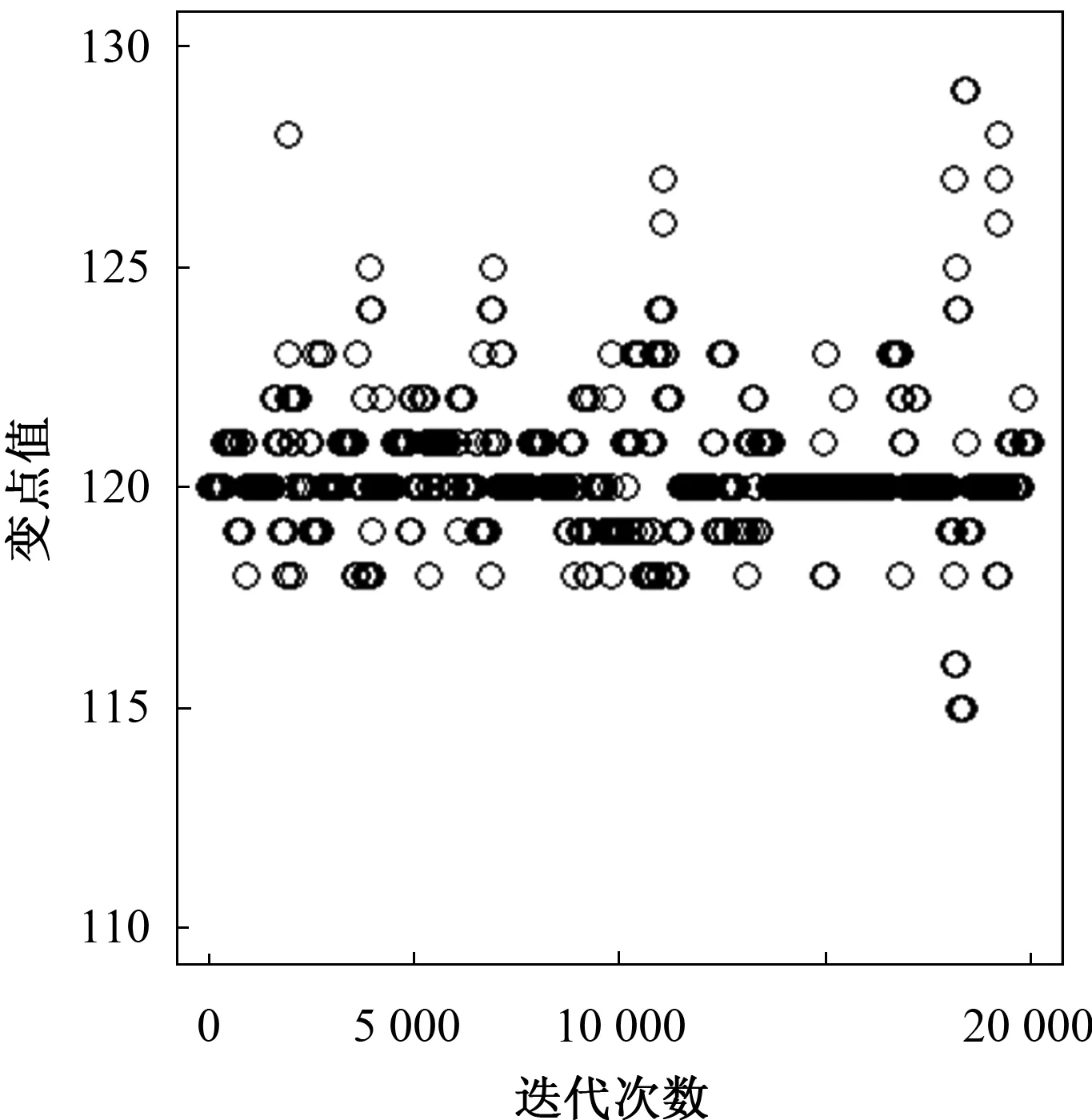
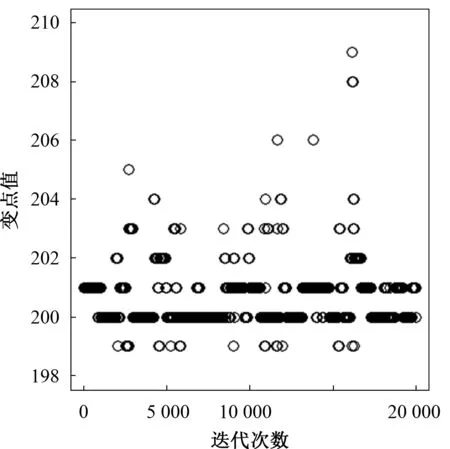
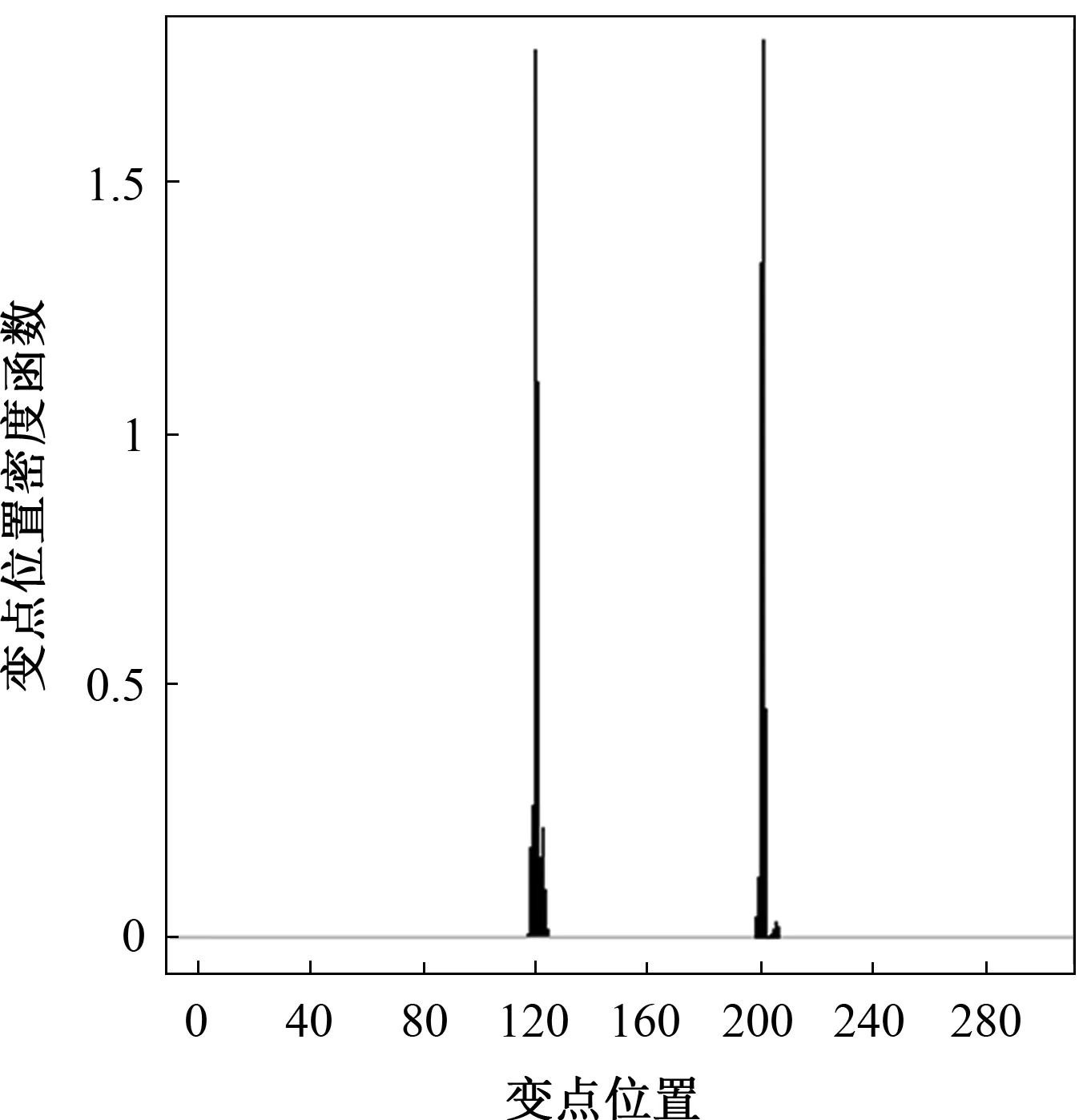
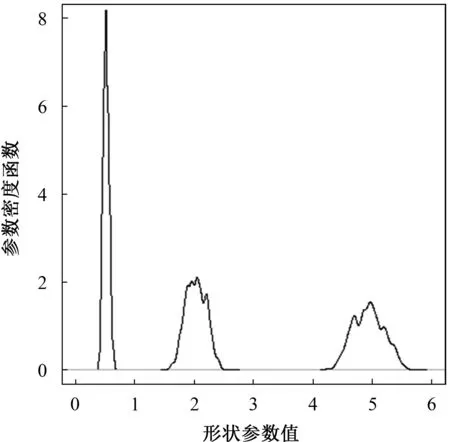
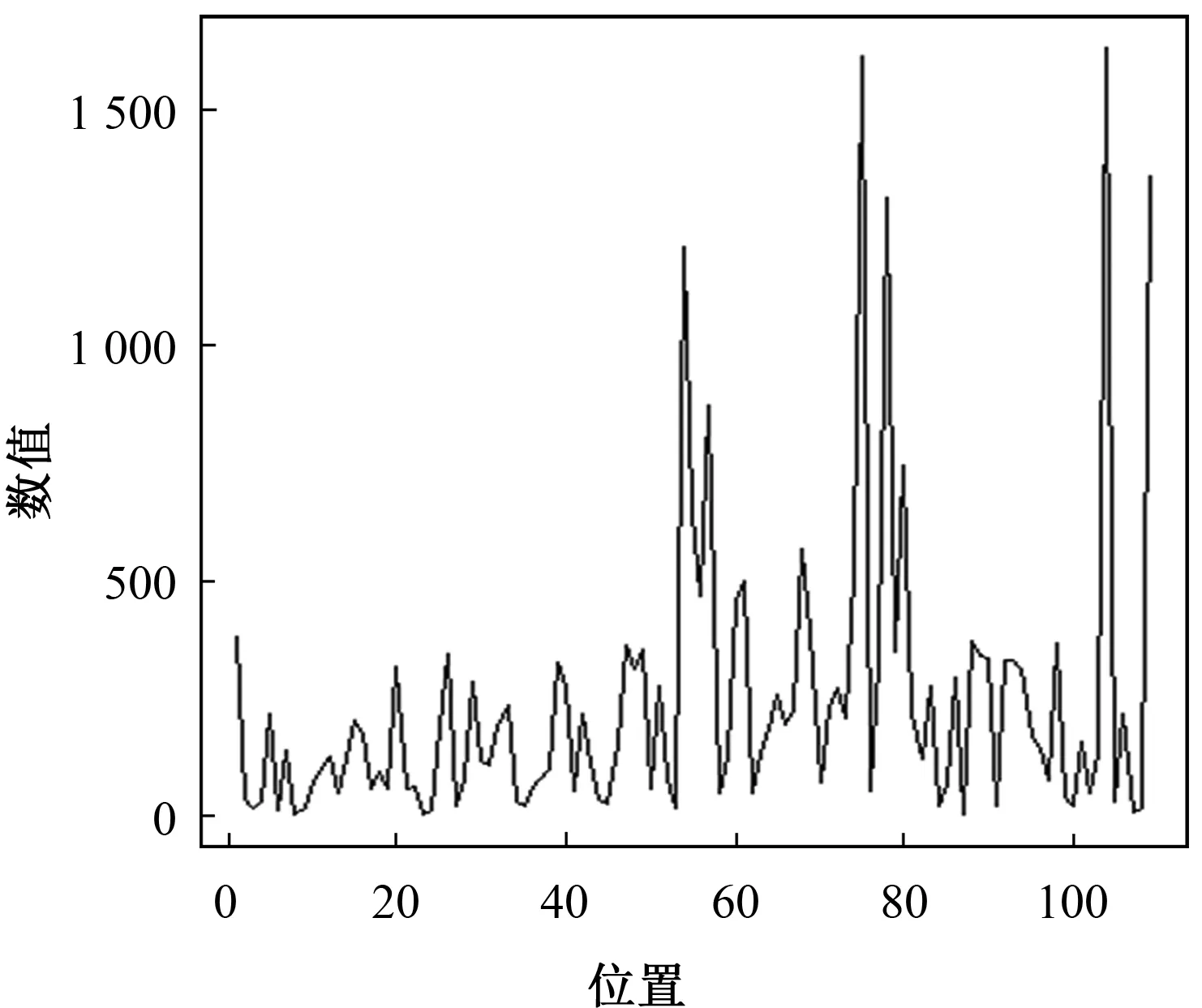
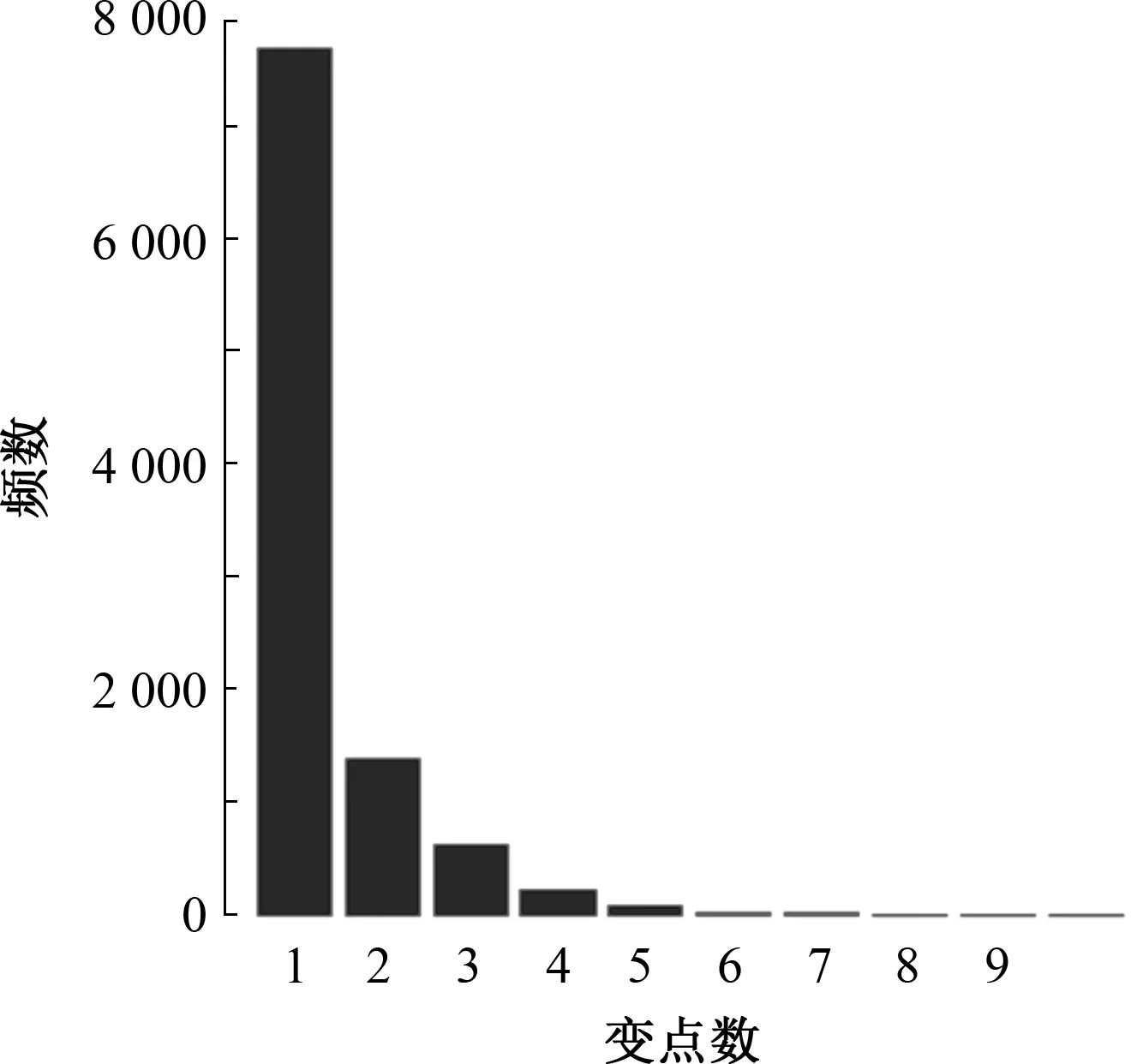
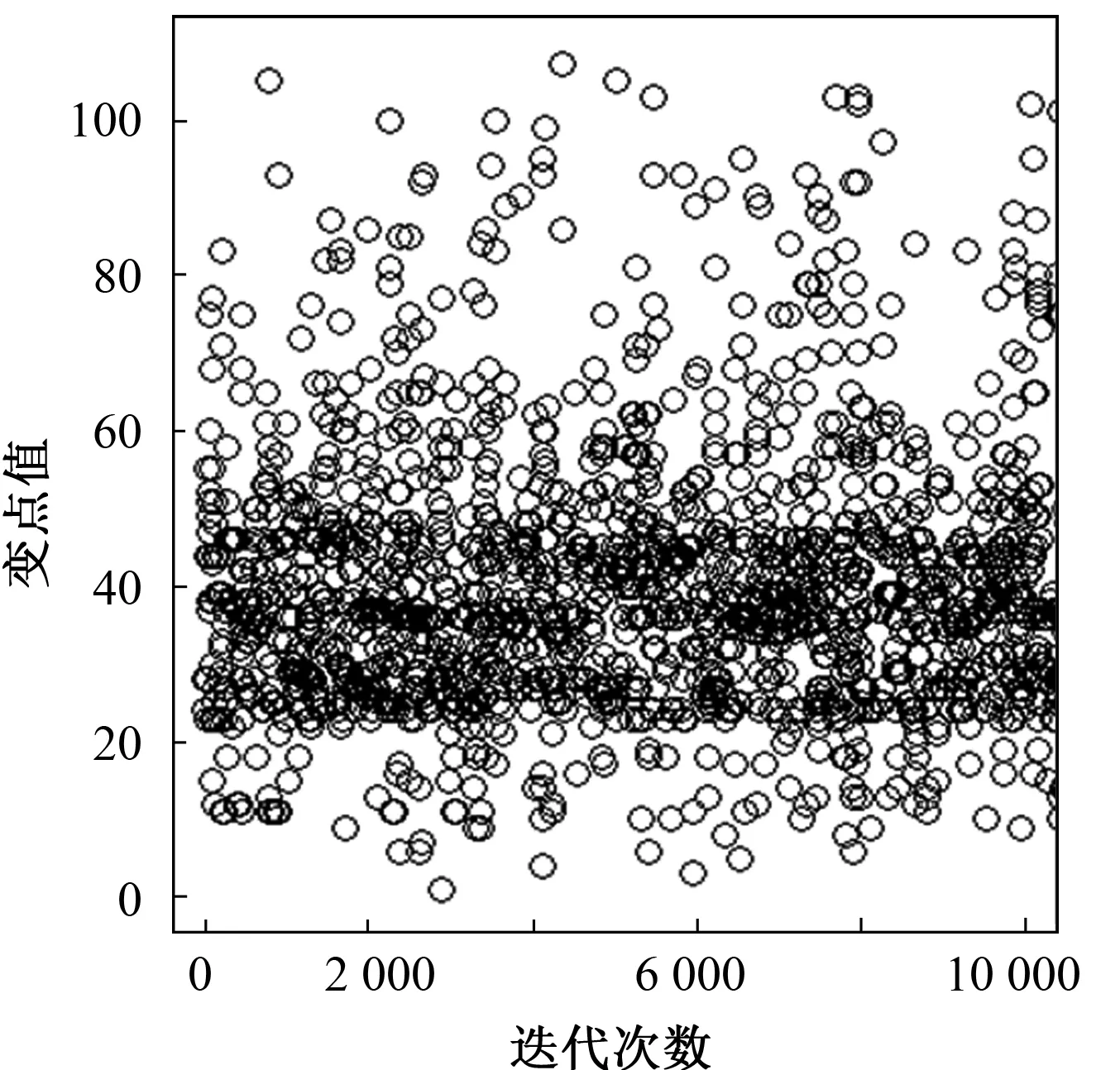
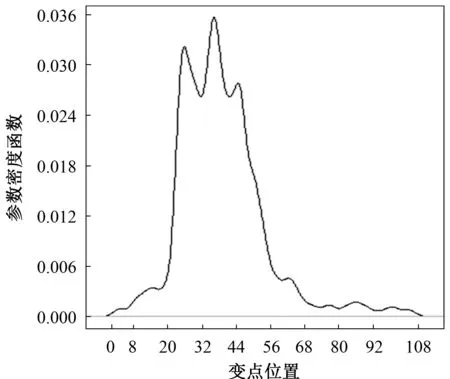
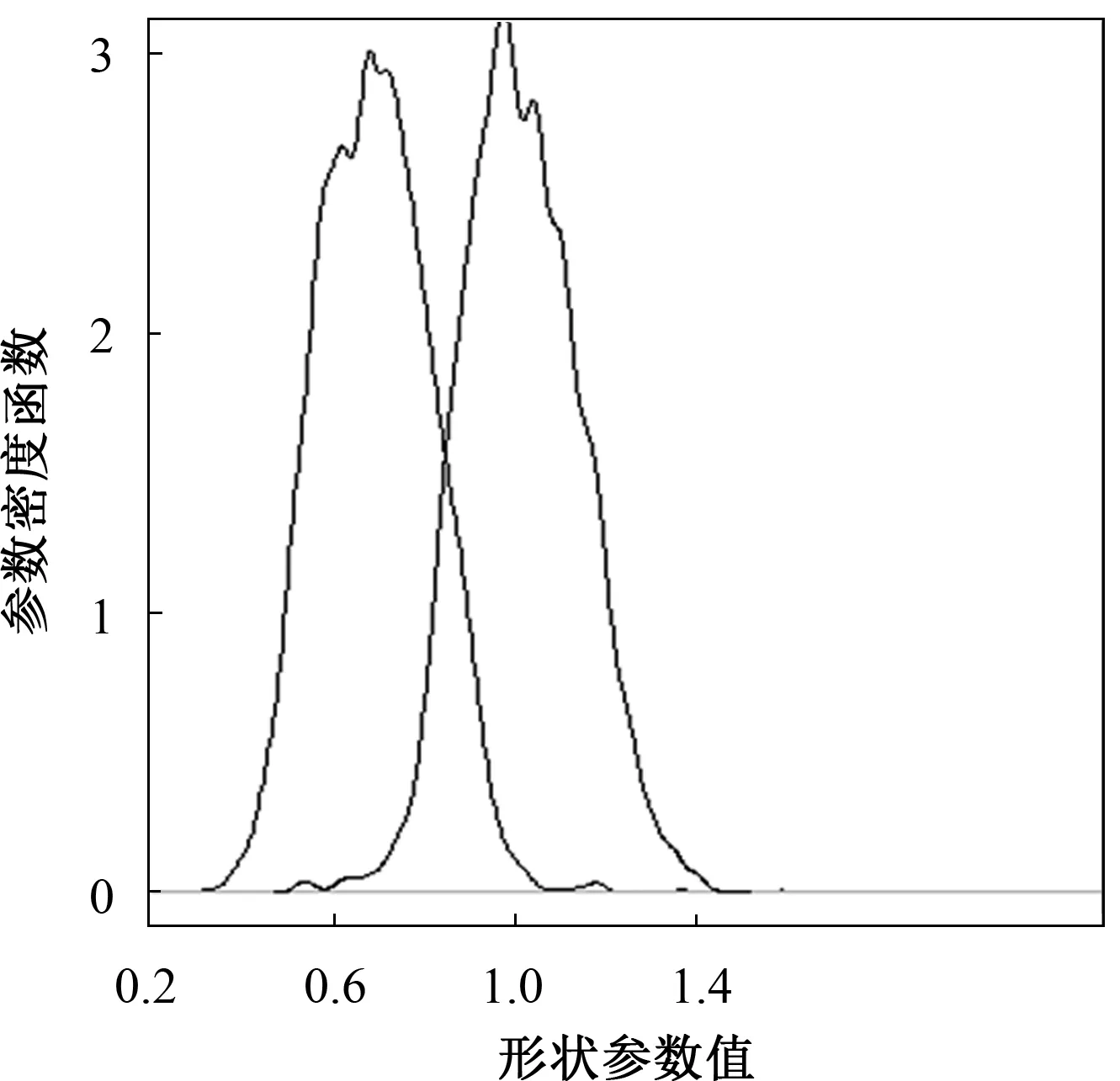
其中0 3)取形状参数{ν1,ν2,…,νk+1}独立同分布于形状参数a和尺度参数b的Gamma分布且均与变点位置相互独立,则 νj~Gamma(a,b),j=1,2,…,k+1。 由贝叶斯分层理论,可得所有未知参数的联合先验分布 p(k,c1c2…ck,ν1ν2…νk+1)=p(k)p(c1c2…ck|k)p(ν1ν2…νk+1|k), 再结合贝叶斯公式可得到样本与参数联合分布的密度函数 (3) 用π(ck|·)表示变点位置ck的满条件分布,同理π(νj|·)表示形状参数νj的满条件分布。由(3)式可得各参数的满条件分布 为获取可逆的蒙特卡洛样本,需要设计合适的移动类型来达到维数的平衡。当形状参数是一个阶梯函数时,本文可基于变点模型设计4种移动类型改变马尔可夫链的状态{k,c1,c2,…,ck,ν1,ν2,…,νk+1}, (a)任意改变一个形状参数值; (b)任意改变一个变点的位置; (c)在{1,2,…,n}{c1,c1,…,ck}上任意选择新增加一个; (d)在{c1,c1,…,ck}中任意选择减少一个。 显然,(c)、(d)的移动会使得马氏链的状态空间维数随着变点数量的改变而变化,因此传统的蒙特卡洛马尔可夫链理论无法适用。用{(a),(b),(c),(d)}表示这些移动的集合,且用m表示移动类型。假设当前状态为x,建议移动类型为m∈{(c),(d)},新状态为x′,通过获得一个独立于x的连续随机变量u且满足dim(x,u)=dim(x′),并利用可逆的确定性函数x′(x,u)设置x′后,可实现状态空间的可逆跳跃。 1995年,GREEN P J探索了4种移动类型的接受概率,并且证明了每个移动类型都能达到马尔可夫链细致平衡的既定目标。当移动类型m∈{(a),(b)}的接受概率 (4) 其中π(x)为状态x时参数后验分布的密度函数,qm(x′,x)为建议密度函数,为简化计算,(4)式中后验分布可分别用似然函数与先验分布的乘积项代替或由相应参数的满条件分布代替。当移动类型m∈{(c),(d)}的接受概率 (5) 下面探讨Gamma分布形状参数多变点模型在每种移动下的接受概率。 Pallow=min{1,A1}, 这里 Pallow=min{1,A2}, 这里,当c′j 当c′j>cj时 对于m=(c),不失一般性,我们假设在区间(cj-1,cj)上增加一个变点c*,则在区间(cj-1,c*)和(c*,cj)上会产生新的参数ν′j,ν′j+1,且νj在ν′j,ν′j+1之间,其关系用权重方式表示为 (c*-cj-1)logν′j+(cj-c*)logν′j+1=(cj-cj-1)logνj。 在此种移动类型的可接受概率表示为 Pallow=min{1,(l.r.b)×(p.r.b)×(pro.r.b)×|(Jaco.b)|}, 其中l.r.b,p.r.b,pro.r.b,Jaco.b分别表示似然比、先验比、建议比、雅可比行列式。 经计算,似然比可直接表示为 先验比 建议比 雅克比行列式 因此随机增加一个新变点c*的接受概率为Pallow=min{1,A3},这里 针对m=(d),同样不失一般性,假设随机选择被减去的变点为cj,则区间(cj-1,cj,cj+1)变为(cj-1,cj+1)。假设ν′j,ν′j+1为区间(cj-1,cj,cj+1)上的2个旧参数,νj为区间(cj-1,cj+1)上的新参数。同理可得,随机减少变点cj的可接受概率为Pallow=min{1,A4},这里, 首先利用RJMCMC算法确定模型中变点的个数。由于变点位置及形状参数的后验分布比较复杂,所以采用Metroplis-Hastings算法对其抽样,再根据前面推导出的相应移动的接受概率,得到模型参数的更新值,具体步骤如下: 1)初始化,给出参数k,ck,λ的初始值,给定超参数a,b,kmax,α的值。 2)利用Metroplis-Hastings算法更新参数{c1,c2,…,ck}。 3)利用Metroplis-Hastings算法更新参数{ν1,ν2,…,νk+1}。 4)每次以bk或dk随机增加或减少一个变点,参数发生相应的改变,最后以概率Pallow接受变点个数的跳跃,实现可逆跳跃过程,其中当0 重复以上迭代步骤,直到最大迭代次数。 随机生成含有300个数据的Gamma分布序列,分为3段: 1~120,121~200,201~300,数据分别服从Gamma(0.5,2),Gamma(2,2),Gamma(5,2)。根据3段形状参数ν不一致,可见存在2个变点,分别在120处和200处,3段Gamma分布参数分别为(0.5,2),(2,2),(5,2)。300个随机数据模拟图如图1所示。设定参数的初始值k=3,c1=50,c2=150,c3=180,ν1,ν2,…,ν4取初始分段上的均值,超参数kmax=10,α=5a=25/4,b=5/4。迭代20 000次算法,去掉前10 000次,用后10 000次的结果计算变点个数的后验概率,得出的变点个数估计如图2所示。 图1 两变点的Gamma分布数据模拟图 图2 变点个数估计直方图 由图2可知,变点个数为2的后验概率最大,因此确定300个Gamma分布序列的变点个数为2。进一步在变点个数的基础上利用MCMC算法估计变点位置参数和Gamma分布形状参数。通过R软件实现模拟,在模拟的过程中进行50 000次迭代抽样,为保证参数的收敛性,舍弃前30 000次抽样,根据后20 000次结果进行统计分析,20 000次变点位置参数和形状参数迭代过程如图3和图4所示。 图3 变点位置c1的迭代抽样过程 图4 变点位置c2的迭代抽样过程 两变点位置的后验密度分布如图5所示,两个变点下的形状参数的后验分布如图6所示。由图5可知,变点位置的后验密度分布有2个峰,分别在120,200附近;由图6可知,形状参数的后验密度分布有3个峰,分别在0.5,2,5附近。由众数后验估计可得变点位置c1,c2为120、200,3个形状参数ν1,ν2,ν3近似为0.5、2、5。这与真实的变点位置及Gamma分布形状参数相符,说明RJMCMC算法对Gamma分布形状参数多变点检测的有效性。 图5 两变点位置的后验密度分布 图6 两变点形状参数的后验密度分布 MAGUIRE B A等[24-25]对英国在1875年12月6日至1951年5月29日期间发生的造成10人以上死亡的煤矿爆炸的时间间隔进行了研究(如图7所示),得出结论:这组数据可能存在一个变点在1890年。随后RAMANAYAKE A[18]又验证了这109个数据服从Gamma分布,进一步证实了在第45个位置(即对应1890年)发生了突变并估计出突变前的形状参数为0.629,突变后的形状参数为1.036。 图7 英国煤矿爆炸数据折线图 现在根据RJMCMC算法对这组数据的变点个数进行检测,变点个数的估计如图8所示,109个数据中存在1个变点的后验概率最大,表明1875年至1951年间发生了一次明显的变化。接下来在变点个数为1的基础上估计变点位置c1及变点前后的形状参数ν1、ν2。 图8 变点个数估计直方图 变点位置c1的迭代抽样过程如图9所示,变点位置的后验密度分布如图10所示,变点前后的形状参数ν1、ν2的后验密度分布如图11所示。由图10和图11,利用最大后验估计法进行分析,可知变点的位置在44附近(即在1890年附近),变点前后的形状参数ν1在0.63附近且ν2在1附近。这与 RAMANAYAKE A[18]的研究结果基本相符,进一步表明了该方法对伽马分布参数变点检测的有效性。 图9 变点位置的迭代抽样图 图10 变点位置c1的后验分布图 图11 形状参数ν1、ν2的后验分布图 本文基于贝叶斯方法和RJMCMC算法对Gamma分布形状参数多变点模型进行变点检测。首先给出了Gamma分布形状参数多变点模型,确定各参数的先验分布,由贝叶斯分层理论将样本与参数的联合分布以乘积项的形式表示。然后针对变点模型设计4种移动,并分别得到其接受概率的表达式,建立RJMCMC算法。最后利用该算法和MCMC算法得到变点个数的确定以及变点位置和形状参数的后验估计。仿真模拟和实例的结果都说明了RJMCMC算法对Gamma分布形状参数多变点模型变点个数确定的有效性。 目前,研究还存在一些不足之处:①没有进一步研究RJMCMC算法的收敛性,可能会出现由于计算量较大,算法耗时较长的情形;②本文考虑的Gamma分布多变点模型有尺度参数不发生变化的假定,算法仅实现了变点位置和形状参数的估计,而实际数据往往与假定条件存在着些许偏差,所以如何利用RJMCMC算法更好地结合伽马分布的两个参数进行的多变点检测有待进一步研究。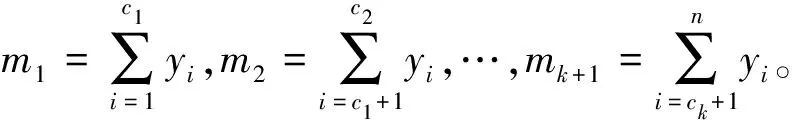
3 基于RJMCMC算法的参数估计
3.1 RJMCMC算法
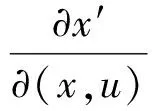
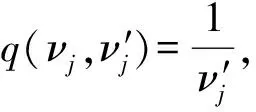
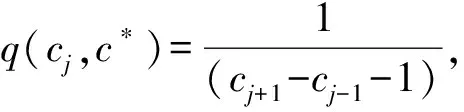
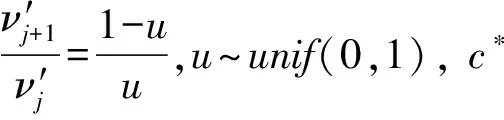
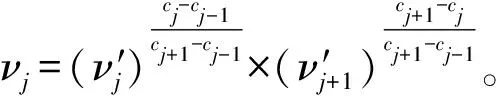
3.2 参数估计

4 实证研究
4.1 仿真模拟
4.2 英国煤矿灾害
5 总结
