基于演化博弈的政府鼓励条件下共享停车行为分析

贾富强，李引珍，杨信丰，马昌喜，代存杰

(兰州交通大学，交通运输学院，兰州730070)

0 引言

目前，停车难问题已是各大城市面临的主要问题，共享停车作为一种合理利用不同区停车位需求和空闲互补而缓解停车位难问题的有效措施被广泛利用[1]。季彦婕等[2]从出行成本入手通过出行者和停车场管理者之间的博弈来研究共享停车位效果。高良鹏等[3]对弹性停车激励机制下共享停车竞价行为演化机理进行了研究。张文会等[4]从停车需求、平均步行距离等方面对居住区共享停车泊位利用率的提升问题进行了研究。孙会君等[5]在考虑停车位租用成本的基础上，提出针对停车位租用和分配统一决策且平台利益最大化的整数规划停车位分配模型。段满珍[6]分析了驾驶人、停车位供应者和共享停车管理平台之间的博弈关系、博弈模型基本式和博弈均衡解。彭勇等[7]建立了两方博弈参与、三方博弈参与及三方合作参与的收益分配模型。王洪飞[8]建立政府、企业和停车位拥有者三方演化博弈模型，仿真探讨三方主体的演化路径及不同策略选择对共享停车产业推广的影响。

现有共享停车匹配问题更多关注于共享停车位和收益分配，鲜有考虑出行者和停车位共享者之间的博弈现象。引入演化博弈建立两方参与共享停车演化博弈模型，分析共享停车中行为主体的决策过程和演化趋势，揭示不同收益条件、不同决策行为选择及其影响下各参与方对共享停车的促进和抑制作用，为推进共享停车发展、缓解停车难问题寻求解决方法。

1 模型构建

1.1 符号说明

Cd——出行者驾车出行时的成本；

Cnp——出行者停车成本；

Cg——车位拥有者支出的固定成本；

Fs——出行者使用共享停车位时的节约成本；

Ce——出行者不使用共享停车平台停车时需要支付的额外费用；

Cf——车位拥有者让不使用共享停车平台的出行者选择共享停车位时额外支付费用；

B——政府反馈盈利，有B=Bd+Bs，其中，Bs表示政府分配给共享车位拥有者的费用，Bd表示政府分配给使用共享停车平台出行者的费用。

1.2 模型假设

为构建共享停车演化博弈模型，假设如下：

(1)假设出行者和停车位拥有者都是有限理性的，都能通过自主学习使共享停车演化博弈达到稳定状态，假定政府鼓励下平台自身盈利并能给出行者和车位拥有者带来反馈收益。

(2)已知出行者T,有“使用”“不使用”共享停车两种策略，记ST={su,snu}，且选择两种策略的比例分别为x和(1-x)，x∈[0,1]，出行者驾车成本为Cd，停车成本为Cnp。

(3)已知车位拥有者P有“共享”“不共享”停车位两种策略，记SP={ss,sns}，且选择两种策略的比例分别为y和(1-y)，y∈[0,1]，车位拥有者固定支出成本为Cg，选择共享停车位后会获利Bs。

(4)出行者选择使用共享停车会获得收益，该收益包括两部分，一部分为使用共享停车后的停车为节约成本Fs，另一部分为政府反馈的收益Bd。不使用共享停车，则不会获得节约成本；如果选择在共享停车位停车，则需要支付额外费用Ce。

(5)如果出行者不使用共享停车平台而在共享停车位停车，需要支付车位共享者停车费用；此时为了促进共享者与使用共享平台的出行者匹配，共享者在获得出行者停车费用的同时，需要额外支付一部分费用Cf。

(6)共享停车平台因为受政府支持等处于盈利状态，为了吸引出行者使用平台，政府将部分盈利B分配给出行者和车位拥有者，即B=Bd+Bs。

1.3 收益矩阵

根据问题描述和假设，构建共享停车双方演化博弈支付矩阵，如表1所示。

表1 共享停车演化博弈支付矩阵Table 1 Evolutionary game payoff Matrix for shared parking

2 演化博弈分析

2.1 复制动态方程

共享停车演化博弈系统中各主体策略的动态变化趋势和速度是有限理性博弈分析的核心，根据文献[9]并结合表1支付矩阵，构建共享停车双方演化博弈模型复制动态如下。

(1)出行者

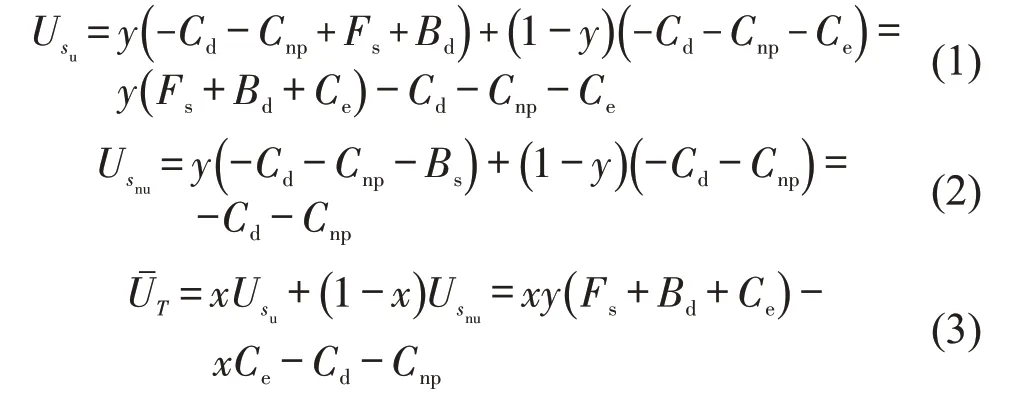
Usnu——出行者不使用共享停车平台时的收益；

(2)车位拥有者

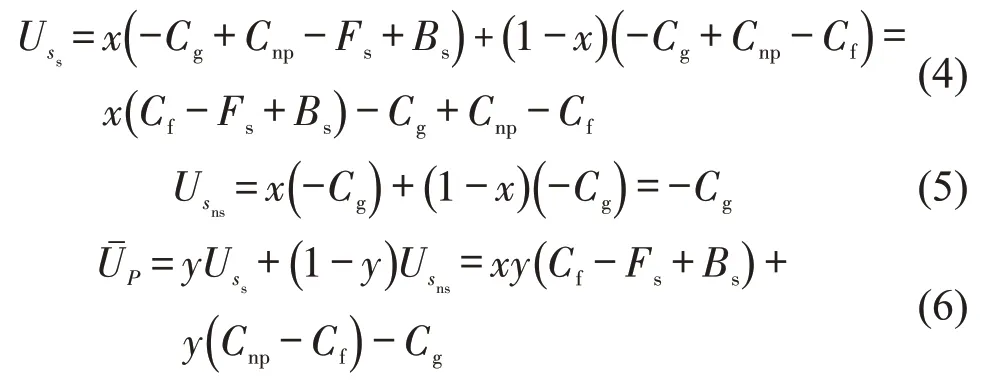
可得系统复制动态方式分别为

根据式(7)和式(8)，计算得雅克比矩阵J及其行列式det(J)和迹tr(J)分别为

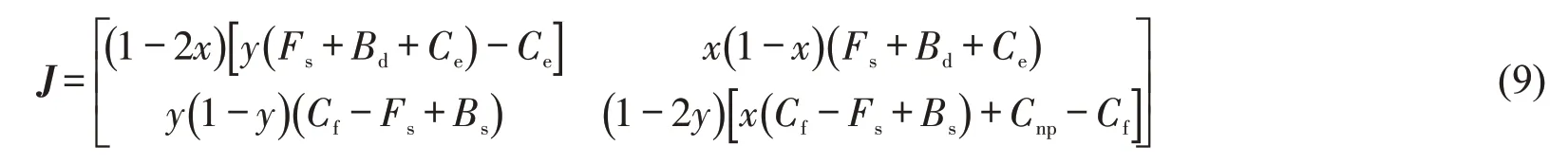
2.2 演化稳定性分析

根据演化博弈和Lyapunov稳定性理论[10]可知，要得到双方的演化博弈稳定策略(ESS)，则有F′(x)<0，F′(y)<0，存在(0,0)、(0,1)、(1,0)、(1,1)和(x∗,y∗)这5个均衡点，将上述均衡点分别带入式(10)和式(11)得行列式det(J)和迹tr(J)如表2所示。

表2 共享停车演化博弈各均衡点状态分析Table 2 State analysis of equilibrium points in evolutionary game of shared parking

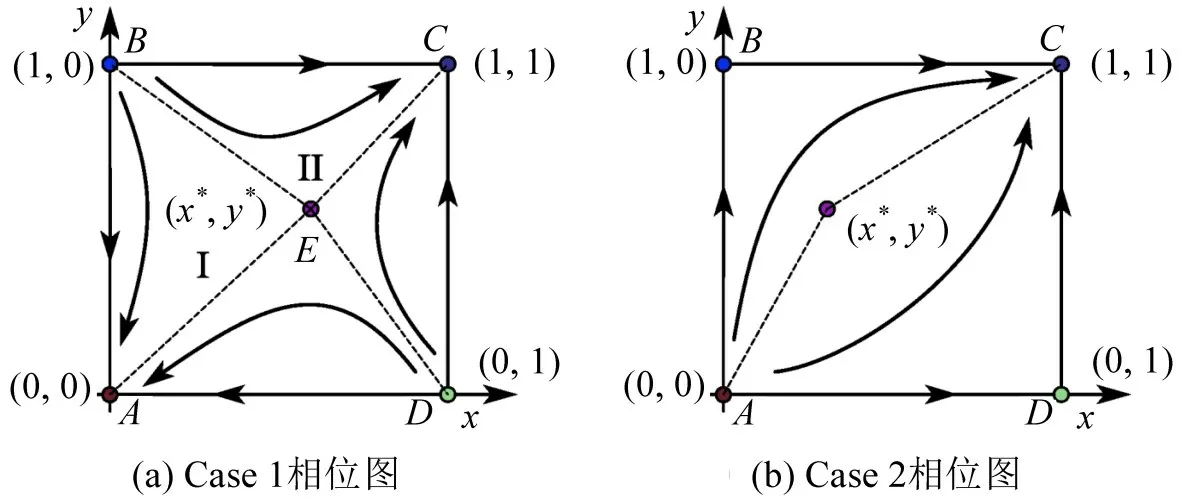
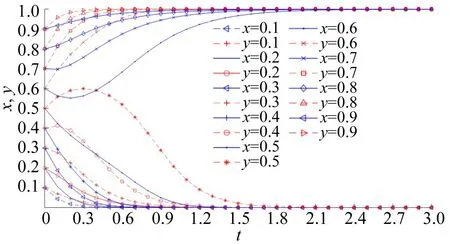
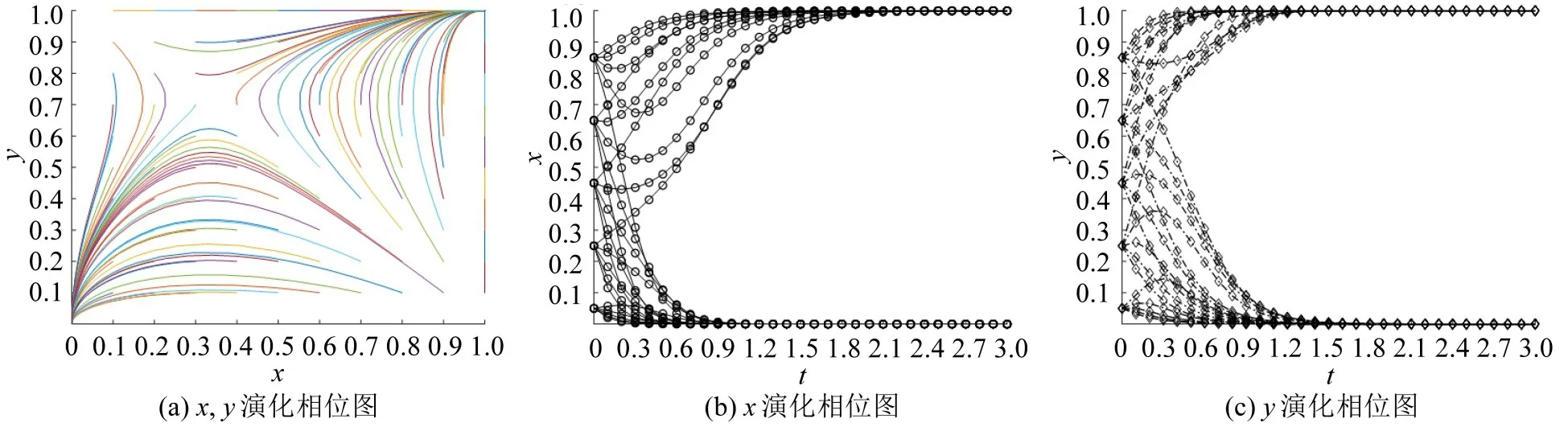
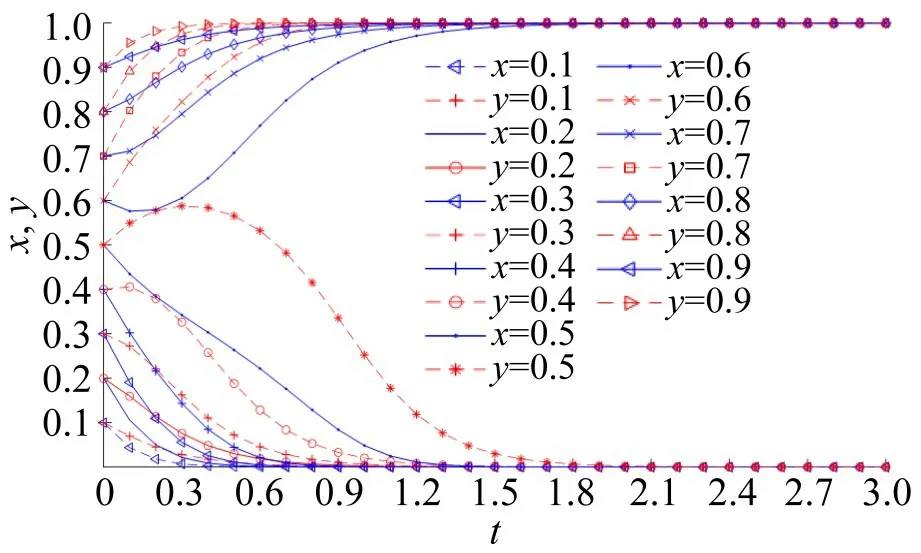
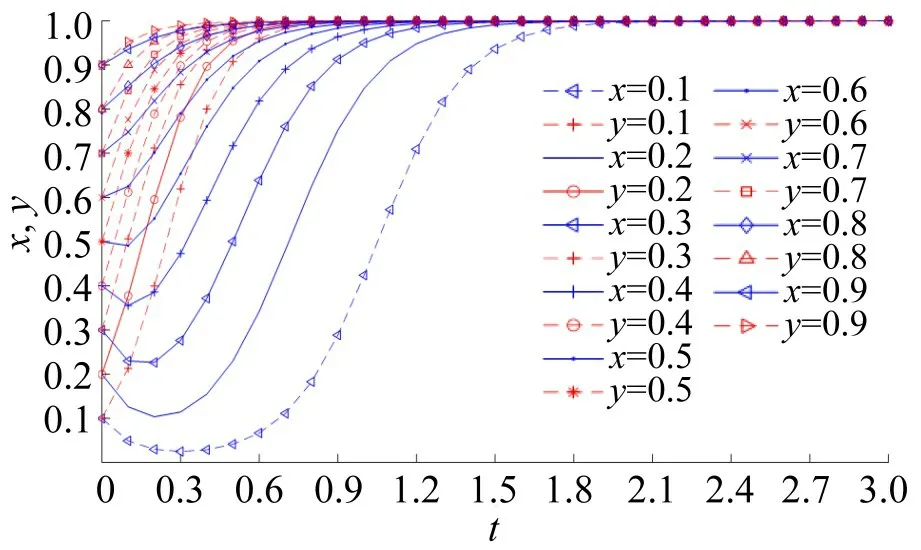
由于Cd>0，Cnp>0，Cg>0，Bs>0，Bd>0，Fs>0，Ce>0，Cf>0，达到均衡状态时有0 ≤x∗,y∗≤1，即，因Ce

Case 1 当Cf>Cnp，Cf>Fs-Bs，Cnp>Fs-Bs时，有。

Case 2 当CfFs-Bs且Fs>Bs时，有Cf-Fs+Bs<0，Cf-Cnp<0，。

Case 1和Case 2对应det(J)和tr(J)及演化博弈均衡状态情况如表3所示。

表3 共享停车演化博弈各均衡结果Table 3 Equilibrium results of evolutionary game of shared parking

由表3 演化均衡结果可知：Case 1 中当Cf>Cnp时，因车位拥有者共享停车位时的收益小于不共享时收益，故车位拥有者在出行者不使用共享停车平台前提下选择不共享，使博弈向(不使用，不共享)演化，如出行者使用平台则博弈将向(使用，共享)演化，此时存在两个ESS；Case 2中当Cf

图1 各情形演化相位图Fig.1 Evolutionary phase diagram of various scenarios

通过上述两种演化情形分析可知，参数变化对Cace 1中演化过程及结果影响较大。从图1(a)中可以看出，演化最终达到的稳定状态与图示区域I(四边形ABED)和区域II(四边形BCDE)的面积有关，记区域I 的面积为S1，区域II 的面积为S2。当S1>S2时，系统收敛于不使用不共享(0,0)状态的概率大；当S1

各参数变化对演化博弈过程影响详细情况如表4所示。

表4 参数对共享停车演化博弈均衡状态影响分析Table 4 Effect of parameters on equilibrium of evolutionary game of shared parking

表4中Cf、Cnp、Ce、Fs、Bs和Bd等6个参数变化对演化博弈结果有影响，当减少共享停车位匹配过程中出行者额外支付费用Ce、车位拥有者额外支付费用Cf或当停车费用Cnp、出行者获得反馈收益Bs和车位拥有者获得反馈收益Bd增加时，演化博弈均可以促使稳定点(使用、共享)的形成，反之演化博弈向(不使用、不共享)发展。同时，可通过调节共享停车节约成本Fs有效促使理想演化稳定点(使用、共享)的形成。

3 演化博弈数值仿真

为分析不同情形下出行者和车位拥有者演化动态及策略变化，进行数值仿真。

(1)对Case 1 进行仿真，当满足Cf>Cnp，Cf>Fs-Bs，Cnp>Fs-Bs时，令Fs>Bs，有(Cf-Fs+Bs)>(Cf-Cnp)>0，设置参数值为Cd=15，Cnp=10，Cg=15，Bs=2，Bd=2，Fs=4，Ce=10，Cf=15，此时双方演化相位如图2所示。

图2 Fs>Bs 演化相位图Fig.2 Evolutionary phase diagram of Fs>Bs

由图2 可知，随进程可达到稳定演化均衡状态，在不同的初始比例条件下系统演化的结果不同，存在混合均衡点(x∗,y∗)，且x∗=0.385,y∗=0.625，当初始比例小于混合策略时，随着演化时序最终稳定于ESS(不使用，不共享)；当初始比例大于混合策略时，随着演化时序最终稳定于ESS(使用，共享)。

为进一步分析出行者和车位拥有者在不同初始比例下的演化过程，对Fs>Bs时不同比例进行演化对比，其结果如图3所示。

由图3 可知，在等初始比例情况下，出行者和共享停车位演化步调一致，同时向(不使用，不共享)或(使用，共享)演化，最终达到演化均衡状态。

(2)对Case 1 进行仿真，当满足Cf>Cnp，Cf>Fs-Bs，Cnp>Fs-Bs时，令Fs(Cf-Cnp)>0，设置参数Cd=15，Cnp=10，Cg=15，Bs=2，Bd=2，Fs=1，Ce=10，Cf=15，此时双方演化相位如图4所示。

图4 Fs

由图4可知，随着演化进程可以达到稳定演化状态，在不同的初始比例条件下系统演化的结果不同，存在混合均衡点(x∗,y∗)，且x∗=0.313,y∗=0.769，当初始比例小于混合策略时，随着演化时序最终稳定于ESS(不使用，不共享)；当初始比例大于混合策略时，随着演化时序最终稳定于ESS(使用，共享)，但因x∗与y∗两者相差较大，随着初始比例的增加，演化波动性比较大，双方演化收敛到稳定状态的时间较长。

同样，按照不同比例对比Fs

图5 Fs

由图5 可知，在等初始比例情况下，出行者和共享停车位演化步调一致，同时向(不使用，不共享)或(使用，共享)演化，最终达到演化均衡状态。当初始比例较低时，出行者演化收敛速率比车位拥有者快，随着初始比例的增加车位拥有者的演化收敛速率明显快于出行者。

(3)对Case 1 进行仿真，当满足Cf>Cnp，Cf>Fs-Bs，Cnp>Fs-Bs时，令Fs=Bs，有(Cf-Fs+Bs)>(Cf-Cnp)>0，设置参数Cd=15，Cnp=10，Cg=15，Bs=2，Bd=2，Fs=2，Ce=10，Cf=15，此时双方演化相位如图6所示。

图6 Fs=Bs 演化相位图Fig.6 Evolutionary phase diagram of Fs=Bs

由图6可知，随着演化进程可以达到稳定演化均衡状态，在不同的初始比例条件下系统演化的结果不同，存在混合均衡点(x∗,y∗)，且x∗=0.333,y∗=0.714，整个演化过程中，演化波动性变化幅度介于FsBs之间。同样，按照不同比例对比Fs=Bs时双方动态演化过程，结果如图7所示。

图7 Fs=Bs 时不同初始比例情形下演化时序Fig.7 Evolutionary time series under different initial ratios of Fs=Bs

由图7可知，在等初始比例情况下双方演化步调一致，同时向(不使用，不共享)或(使用，共享)演化，最终达到演化均衡状态。随着初始比例的增加演化波动性比较大，双方演化收敛到稳定状态的时间较长。

(4)对Case 2 进行仿真。满足CfFs-Bs且Fs>Bs，有Cf-Fs+Bs<0,Cf-Cnp<0,(Cf-Fs+Bs)>(Cf-Cnp),设置参数Cd=15，Cnp=10，Cg=15，Bs=2，Bd=2，Fs=4，Ce=10，Cf=1，此时双方演化相位如图8所示。

由图8可知，随着演化进程可以达到稳定演化均衡状态(使用，共享)，但在整个过程中出行者演化收敛到稳定状态的速度较慢，且明显慢于车位拥有者演化收敛速率，说明在此种情形下，出行者对共享停车的敏感程度低于共享者。

图8 Case 2演化相位图Fig.8 Evolutionary phase diagram of Case 2

按照不同比例对比Fs=Bs时双方动态演化过程，结果如图9所示。由图9可知，在等初始比例情况下出行者和共享停车位演化步调不一致，但随着演化时序的增加两者都向(使用，共享)演化，最终达到演化均衡状态。同样，当出行者初始比例较小时出行者演化波动性较大，但随初始比例的增大波动性减少，最终向共享演化并趋于稳定。

图9 Case 2时不同初始比例情形下演化时序Fig.9 Time series under different initial ratios in case of Case 2

通过上述情形数值仿真对比发现，在不同的初始比例情形下出行者和车位拥有者均能通过不断学习最终演化至稳定均衡状态。如想演化至(使用，共享)状态，则需较高的初始比例。同时在上述4种仿真中假定Bd=Bs，为了进一步分析收益分配比例对两者演化动态的影响，在此设Bd=αB，Bd=(1-α)B，其中，α表示平台分配给出行者的收益比例，1-α表示平台分享给车位拥有者的比例，以第(1)种仿真情形为例，进行不同分配比例α的演化动态分析，详细变化如图10所示。

图10 不同分配比例α 演化时序图Fig.10 Time series of evolution at different allocative ratios α

通过图10 可知，分配比例α的变化不会影响最终的演化均衡状态，但会影响演化过程中达到演化稳定状态的时间。分配比例α的变化对初始比例较低时的演化趋势影响不大，普遍为出行者收敛速率快于车位拥有者演化收敛速率；说明因初始比例较低，双方群体中大多数选择策略为(不使用，不共享)，因为从众心理故分配比例对演化趋势影响不大。分配比例α的变化对高初始比例演化趋势和演化速率影响较大，且比例越大影响程度最明显；说明初始比例大时，双方群体中多数选择策略为(使用，共享)，因从众心理分配比例的大小影响演化趋势和演化速率。

综合考虑参数影响分析中无法定性分析使用共享停车后停车位节约成本Fs的变化对博弈演化方向的影响，在此从定量分析角度仿真分析不同共享停车节约成本Fs对演化趋势的影响，设置参数Cd=15，Cnp=10，Cg=15，Ce=10，Cf=15，B=4，α=0.5。分别对初始比例x=y=0.55 时，Fs=0、Fs=2、Fs=4、Fs=8、Fs=10、Fs=12 等6 种情形进行演化动态分析，详细变化如图11所示。

图11 不同节约成本Fs 情形下演化时序Fig.11 Evolutionary time series under different cost savings scenarios Fs

通过图11 可知，到最终演化均衡稳定状态为(不使用，不共享)时出行者选择“不使用”策略的收敛速度随共享节约成本的增加而加快，同样车位拥有者选择“不共享”策略的收敛速度随共享节约成本的增加而加快；当最终演化均衡状态为(共享，使用)时，出行者选择“使用”策略的收敛速度随共享节约成本的增加而加快，而车位拥有者选择“共享”策略的收敛速度随共享节约成本的增加而变缓。合理的共享停车节约成本可以促使稳定点(使用，共享)的形成，但当该节约成本大于某个值时，演化方向会向稳定点(不使用，不共享)突变，如Fs=10时最终的稳定均衡点为(不使用，不共享)。可见共享停车节约成本对出行者选择使用共享停车起促进作用，而对车位拥有者共享停车位起抑制作用，所以在共享停车运营管理中，除了适当增加共享停车节约成本吸引出行者使用共享停车平台外，还应该从增加共享反馈收益方面提升车位拥有者共享停车位的积极性。不能一味地通过增加共享停车节约成本来促使理性稳定点(使用，共享)的形成，而应该通过充分的市场调研确定最佳共享节约停车成本。

4 结论

本文构建了共享停车演化博弈模型，分析了双方博弈稳定性，着重研究了政府鼓励措施下不同策略选择比例和参数对共享停车演化博弈的影响，得出如下结论：

(1)在政府鼓励措施下，如车位拥有者处于相对收益状态，共享停车博弈会向(使用，共享)状态演化；如处于损失状态，则共享停车博弈会向(使用，共享)和(不使用，不共享)状态演化；政府对车位拥有者的激励和惩罚力度影响着共享停车的发展。

(2)不同初始比例情形下，双边演化博弈最终演化至稳定均衡状态，但要达到(使用，共享)状态则需要较高初始比例，可以通过提高收益和减少成本等措施诱导出行者和车位拥有者使用共享停车平台。

(3)政府的鼓励措施对共享停车政策影响较大，且平台收益分配比例对高初始比例共享停车演化过程影响较大，共享平台可通过制定合理的分配比例来促进演化达到理想状态。

本文在研究时将假定政府对共享停车持鼓励态度，没有细化考虑政府对共享停车不鼓励态度的影响，在今后的研究中将从出行者、车位拥有者和政府三方演化的角度深入研究。