基于秩最小化矩阵去噪的船舶轨迹重构方法

刘文，汪文博

(武汉理工大学，a.航运学院；b.内河航运技术湖北省重点实验室，武汉430063)

0 引言

船舶自动识别系统(AIS)是一种用于保障海上运输安全的船舶自动报告系统，可提供各种静态和动态信息，包括船舶位置、航速、吃水深度、装载状态等。这些数据可以被其他船舶及船舶交通服务中心(Vessel Traffic Service Center，VTS)接收，广泛用于船舶之间的避碰、风险评估、轨迹追踪等研究。根据国际海上人命安全公约(International Convention for Safety of Life at Sea，SOLAS)规定，客船及总吨位超过300的国际航船必须安装AIS系统。此外，中华人民共和国海事局(MSA)等相关部门也非常重视安全，为内河船舶配备AIS系统。随着在国际船舶和内河船舶的广泛应用，AIS数据在海上数据分析、航行安全和海上风险评估等方面发挥着不可或缺的作用[1]。

由AIS 数据显示的船舶轨迹数据是避碰研究的重要数据来源之一。SU 等[2]提出一种基于模糊逻辑理论的系统，利用AIS数据对被让路船进行最优舵转向决策。同时，通过与其他AIS 数据的比较，可提供用于船舶异常行为识别的实时数据[3]。此外，历史AIS数据对于船舶航行风险评估具有重要价值。例如，在新加坡海峡，通过AIS 数据可识别危险水域和船舶类型[4]。近年来，AIS 数据被广泛用于船舶轨迹预测，通过机器学习方法进行海上交通调查和安全管理。LI等[5]基于AIS数据开发了一种相似性分组引导的机器学习模型，用于海上时间序列预测。这些应用都依赖于准确的船舶轨迹。

然而，此前的研究表明，AIS 提供的轨迹数据在多数情况下是不准确和不可靠的，根据HARATI M.等[6]对AIS 误差的调查显示，大约30%的船舶曾有过AIS信息不准确的情况。AIS误差的产生受多种因素的影响：第一，由于海况复杂以及定位设备的限制，使得船舶轨迹会出现噪声数据；第二，当处于无定位信号的区域时，船舶轨迹会包含缺失数据；第三，由于AIS 传输时间间隔远低于IMO(International Maritime Organization)标准[6]，船舶轨迹采样率较低，导致轨迹稀疏。若此类数据用于需要依赖于高精度轨迹数据的海上风险评估或数据分析等问题，将影响海员的判断，极大地增加航行风险。因此，量化和重构实际船舶轨迹对于提高AIS的可用性，提高航行安全具有重要意义。

针对基于AIS的船舶轨迹重构问题，QU等[4]提出一种基于牛顿运动定律的数据清洗方法，可有效消除AIS 数据噪声。NGUYEN 等[7]提出一种基于时间序列的分析和校正AIS数据的方法，该方法结合时间序列特征识别和插值修复方法，对直线航行轨迹具有较好的自适应重构能力，但不适用于非线性航行轨迹。SANG等[8]提出一种用于内河船舶轨迹重构的曲线拟合方法。WANG 等[9]提出一种基于最小二乘支持向量机(LS-SVM)的AIS 数据修复方法。然而，上述方法无法在缺失点较多的轨迹上很好地完成轨迹重构。

为填补上述研究空白，本文提出了一种基于秩最小化矩阵去噪的船舶轨迹重构方法。由于内河船舶一般都有固定的航道，轨迹之间具有较强的自相似性，充分利用轨迹的自相似性，可实现高缺失率下更好的轨迹重构效果。研究的贡献在于以下两点：第一，构建了秩最小化矩阵去噪模型，利用轨迹的自相似性重构船舶轨迹，通过1个模型同时实现轨迹缺失补全与去噪；第二，提出的方法在不同缺失比例以及随机缺失和连续缺失两种缺失情境下具有鲁棒性和较强的稳定性。此外，该方法的性能明显优于HALRTC 等轨迹重构方法，并在高缺失率下表现较好的重构效果。

1 相关基本算法

1.1 2D-VMD分解算法

二维变分模态分解(2D-VMD)是在VMD 算法的基础上发展而来的一种非递归自适应分解算法[10]，常用于矩阵分解，可将不同形状或不同方向的多分量矩阵分解为中心频率附近的几个有限带宽，得到多个子模态函数分量(IMF)。其约束变分方程为

为解决上述约束性变分问题，引入二次惩罚因子α和拉格朗日乘子将约束变分问题转变为非约束变分问题，其增广拉格朗日表达式为

式中：λ为拉格朗日乘子；为模态集合；为中心频率集合。则问题转化为

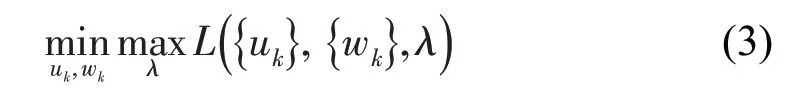
引入交替方向乘子算法(Alternate Direction Method of Multipliers，ADMM)解决上述变分问题，通过迭代更新优化uk，wk及λ求得扩展拉格朗日表达式的“鞍点”。

1.2 PLR去噪算法

基于数据块的秩最小化算法PLR 是一种常用的数据去噪算法，该算法相比于K-SVD[11]、PLOW[12]以及BM3D[13]等具有更好的去噪效果与更快的运行速度[14]。对于矩阵X∈RM×N，本文假设M=N，矩阵可被划分为多个d×d的重叠块。重叠块集合，xi为第i块重叠块。对于每个重叠块xi∈D，称为参照块，其周围n×n范围内均包含个重叠块，选择其中个最相似的块(包含参照块本身)转化为向量。各个参照块的相似块向量堆叠在一起可组成d2×m的相似矩阵。该相似矩阵表示为，其中，S中的列sj,j=1,2,…,m，j为列索引，即由相似块转化的向量。

然后，对相似矩阵S进行去噪。首先，基于主成分分析法得到自适应基，其主成分基为SST的特征向量集合。特征值分解过程为

相似矩阵S中的列向量si近似计算为

式中：t为阈值。则相似块组成的矩阵为

定义秩最小化问题为

式中：μ为正标量；Rank(∙)为X的秩函数。其解为

式中：Y=UAVT为Y的SVD 分解过程，U和V分别为左奇异矩阵和右奇异矩阵；A为奇异值对角矩阵；为Frobenius 范数；为一个对角矩阵，其对角值可通过硬阈值操作得到，即

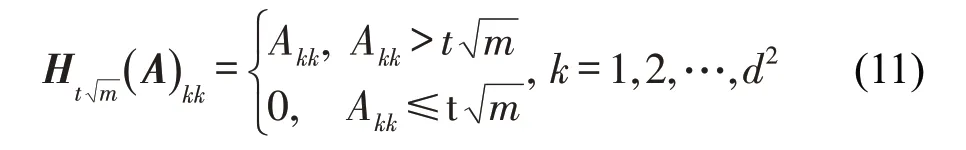
式中，Akk为k行k列的对角值。则去噪后矩阵为

其解为

式中：Q为正交矩阵，满足QTQ=I，I为单位矩阵。

2 基于秩最小化矩阵去噪的船舶轨迹重构模型

2.1 轨迹矩阵构建与预修复

通常，由于船舶航行非匀速以及AIS信号的非等间隔发送，导致船舶轨迹经纬度非等间隔分布，无法针对非均匀分布的轨迹点进行修复。本文将AIS 经纬度数据转化为1 个二维轨迹矩阵，，m1为轨迹数量，m2为每条轨迹的轨迹点数量。对于每条轨迹，设定固定经度范围到，以及等经度间隔τ，将轨迹划分为固定数量轨迹点，其中每个轨迹点的经度均为等间隔划分的固定值，并将其对应的纬度存入矩阵作为各轨迹点数据。假设xi为轨迹矩阵X的第i行数据，为第i行的第j个纬度数据，则。

由于大部分AIS 数据经度并不与轨迹矩阵划分的等间隔轨迹点的经度对应，因此，被划分的各轨迹点对应的纬度数据存在缺失的情况。大量缺失值的存在对于轨迹重构的最终结果具有重要影响，因此，在矩阵分解并进行去噪前需要进行预处理。为补全轨迹矩阵中的缺失值，采用线性插值的方法。假设Ar,k为轨迹矩阵中第r条轨迹k位置的纬度值，Br,k为Ar,k对应的经度值，Ω r为第r条轨迹各轨迹点纬度值集合，线性插值式为

线性插值可以根据插值点的临近数据估计数值，本文希望在保持轨迹主要走向不变的基础上，尽可能精确补全数据，实现缺失值预修复。完成预修复之后，即可得到完整的轨迹矩阵。

2.2 船舶轨迹重构模型构建

为进一步提升船舶轨迹重构的精度，将构建的轨迹矩阵使用2D-VMD 分解为多个IMF 分量。预修复和2D-VMD 分解过程在保证轨迹主要走向不变的前提下均会产生一定误差，这些误差可被认为轨迹噪声。同时，原始轨迹中也包含部分噪声数据。因此，基于矩阵的非局部自相似性，本文使用PLR 算法对各IMF 分量进行矩阵去噪，最后，再对各分量的去噪结果求和，得到最终的去噪结果，在消除预修复与2D-VMD 分解过程带来的误差的同时消除轨迹原始噪声，实现轨迹重构。

本文提出的船舶轨迹重构方法流程如图1所示。

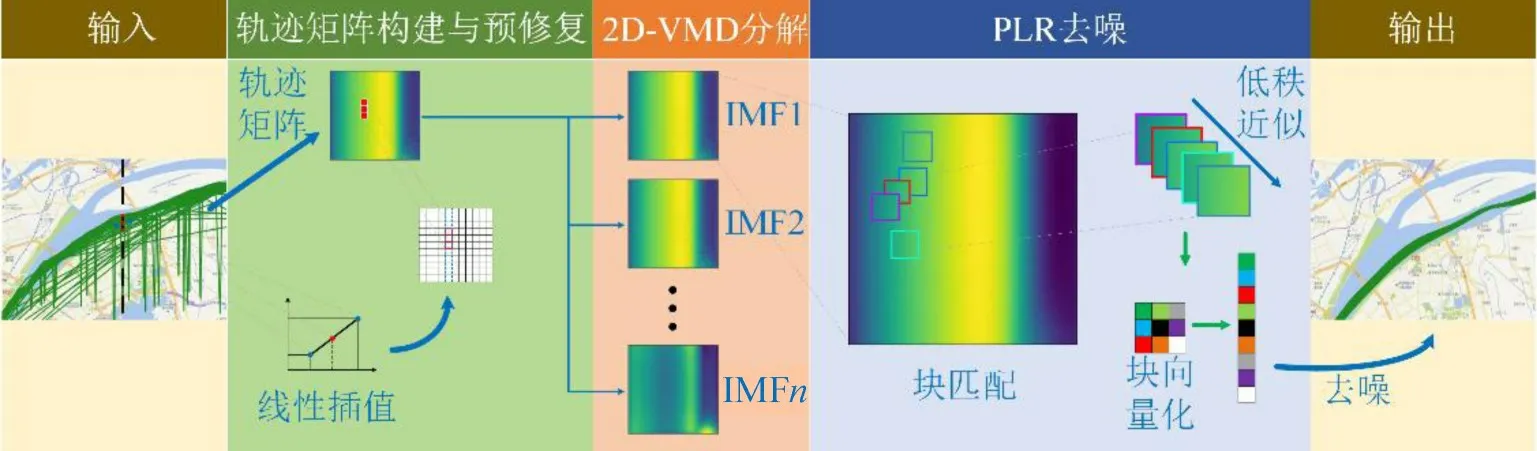
图1 船舶轨迹重构方法流程Fig.1 Process of vessel trajectory reconstruction method

算法基于秩最小化矩阵去噪的船舶轨迹重构方法输入：目标水域AIS数据集S，IMF数量k，重叠块大小d，相似块选取范围n，相似块选取数量m输出：重构后的船舶轨迹集合F1(1)S 各条轨迹通过线性插值实现经度对齐(2)各条轨迹的所属轨迹点对应的纬度值构建轨迹矩阵X(3)通过2D-VMD算法分解轨迹矩阵X 为k 个IMF分量，得到SE=IMF1,IMF2,…,IMFk(4)or j in[1∶k](5)对IMFj 进行PLR去噪，得到去噪结果矩阵Mj(6)End(7)F1 ←合并M1,M2,…,Mk

3 实验结果与分析

3.1 实验设置

为校验本文提出的方法在实际水域中的轨迹重构效果，选取长江武汉段部分水域作为研究区域。该区域起止点经纬度分别为(114.30000，30.57530)，(114.63966，30.56490)，分上行和下行3条航路。本文按上行和下行从AIS 中各选取1000条轨迹数据，并设定经度间隔τ为0.00034，将研究区域的每条轨迹划分为1000 个轨迹点，通过线性插值，构建1000×1000 的轨迹矩阵。

本文实验分为真实实验和模拟实验。真实实验通过使用本文提出的方法对研究水域轨迹进行重构，并与原始轨迹对比，验证重构效果。模拟实验通过按上行和下行各选取1000 条噪声较小、数据较完整的轨迹作为研究对象，按一定比例模拟缺失，分别使用本文提出的方法与其他几种经典轨迹重构方法对研究轨迹进行重构，并将结果进行对比分析，比较各方法重构效果的优劣。

模拟缺失的情境分为随机缺失和连续缺失，分别按10%～80%的缺失比例进行模拟。设定2DVMD 分解得到IMF 数量k=2，PLR 算法d=7，n=35，m=5d2。使用平均绝对百分比误差MAPE和均方根误差RMSE作为结果评价指标。

3.2 对比实验模型

本文选取的对比轨迹重构方法包括：

(1)高精度低秩张量补全(High-Accuracy Low-Rank Tensor Completion，HALRTC)，通过最小化核范数实现补全。

(2)时间正则化矩阵分解(Temporal Regularized Matrix Factorization，TRMF)，一种自回归正则化时间矩阵分解方法。

(3)广义高阶正交迭代的张量分解与补全(Generalized Higher-Order Orthogonal Iteration for Tensor Decomposition and Completion，GHOI)，一种可扩展的核心张量Schatten 1范数最小化方法同时进行张量分解和补全。

(4)基于核范数的低秩矩阵补全(Low-Rank Matrix Completion Based on Nuclear Norm，LRMC)，可从矩阵的输入采样中恢复数据矩阵。

(5)基于离散余弦变换的张量核范数最小化(Tensor Nuclear Norm minimization with Discrete Cosine Transform，TNN-DCT)，通过推导出新的张量管秩、张量谱范数和张量核范数，求解凸规划来完成张量补全。

3.3 基于AIS的船舶轨迹重构实验结果与分析

使用Python 3.9.2 构建模型，完成对研究水域的轨迹重构。为验证本文方法在实际水域中的重构效果，将重构结果与原始轨迹对比，结果如图2所示。

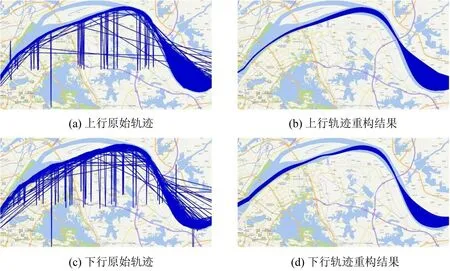
图2 船舶轨迹重构效果对比图Fig.2 Comparisons of vessel trajectory reconstruction

由图2可知，本文提出的方法基本修复了上行及下行原始轨迹中存在的缺失及噪声点，使轨迹重构到正常航道。为了验证本方法的精度与稳定性，上行及下行轨迹在10%～80%比例随机缺失的情境下，本方法及其他5 种对比方法的MAPE 和RMSE评价指标值如表1 和表2所示。根据表1 和表2 的各评价指标值绘制的对比情况如图3所示。为完成张量补全的对比实验，实验将从研究水域轨迹构建的1000×1000 的轨迹矩阵按每50 条轨迹为1 组作为切片转化为50×1000×20 的轨迹张量，在保证轨迹自相似性不被破坏的前提下，实现从轨迹矩阵到张量的转化。

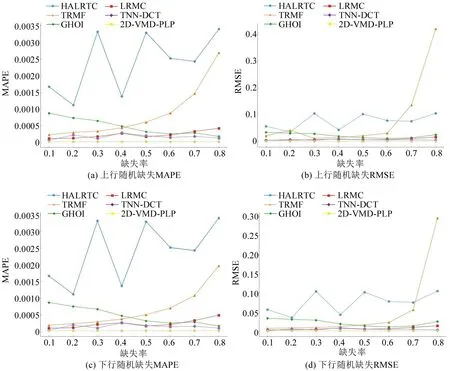
图3 随机缺失轨迹重构效果对比Fig.3 Comparisons of trajectory reconstruction with random missing

表1 上行轨迹随机缺失评价指标(MAPE/RMSE)Table 1 Evaluation criteria in case of random missing in upward trajectory(MAPE/RMSE)

表2 下行轨迹随机缺失评价指标(MAPE/RMSE)Table 2 Evaluation criteria in case of random missing in downward trajectory(MAPE/RMSE)

本文方法在不同比例随机缺失下的MAPE 及RMSE值均小于其他对比方法，且随着缺失比例的提升，变化较小。

上行及下行轨迹在10%～80%比例连续缺失的情境下本方法及其他5 种对比方法的MAPE和RMSE 评价指标值如表3 和表4所示。根据表3 和表4 的各评价指标值绘制的对比情况如图4所示。

图4 连续缺失轨迹重构效果对比Fig.4 Comparisons of trajectory reconstruction with continuous missing

表3 上行轨迹连续缺失评价指标(MAPE/RMSE)Table 3 Evaluation criteria in case of continuous missing in upward trajectory(MAPE/RMSE)

表4 下行轨迹连续缺失评价指标(MAPE/RMSE)Table 4 Evaluation criteria in case of continuous missing in downward trajectory(MAPE/RMSE)

本文方法在不同比例连续缺失下的MAPE 及RMSE值均小于其他对比方法，且随着缺失比例的提升，变化较小。

综上所述，本文方法重构结果相较于其他船舶轨迹重构方法具有更高的精度，更接近于真实值且在不同缺失比例下更加稳定，在高缺失率下拥有更好的重构效果。

4 结论

针对AIS 数据在实际应用中存在的错误数据频发、数据丢包等问题，本文提出基于秩最小化矩阵去噪的船舶轨迹重构方法，该方法可以利用轨迹的自相似性，对研究水域轨迹进行统筹考虑。一方面能够消除原始轨迹中存在的噪声，同时，能够补全轨迹中的缺失值。该方法相较于传统方法对于低质量轨迹的重构具有较强的鲁棒性和更好的重构效果。在上行和下行的轨迹中均能够很好地去除噪声，补全缺失，并且在不同缺失比例以及随机缺失和连续缺失两种情境下稳定性更强，尤其在高缺失率的轨迹重构中表现出较强的鲁棒性和稳定性。重构后的轨迹相比于真实轨迹偏差较小，且轨迹位置固定在航道内，符合研究水域航道走向。