基于安全势场的网联自主车辆跟驰行为决策及模型

2022-03-02贾彦峰曲大义赵梓旭王韬宋慧

交通运输系统工程与信息 2022年1期

贾彦峰，曲大义，赵梓旭，王韬，宋慧

(青岛理工大学，机械与汽车工程学院，山东青岛266520)

0 引言

人工势场的概念出现在20世纪末，首先被应用于机器人的路径规划[1]，受此启发，SATTEL 等[2]将机器人弹性带的概念扩展到自主车辆运动规划中，并基于势场理论提出了运动规划算法；NI 等[3]从宏观和微观的角度证明了人工势场在交通领域的客观性和普遍性，并使用NGSIM 数据标定跟驰模型的参数；HSU 等[4]基于引力场的概念，提出一种新的重力跟驰模型，该模型通过与车辆及其前方空间有关的一系列吸引力和斥力描述汽车跟驰行为；WOLF 等[5]基于人工势场理论将车辆势场构建成楔形，分析不同速度下的车辆具有不同的速度势，以此作为驾驶员辅助设备中的附加输入；曲大义等[6]分析了车辆交互的分子动力学特性，通过相互作用势函数建立分子跟驰模型，并验证了模型具有较高的精确度；LI等[7]从刺激响应的角度提出了一种简化的人工势场跟驰模型，但模型中考虑的因素相对简单；YANG 等[8]考虑到横向距离对跟驰车辆的影响，并将单个车辆表示为电场中的单位点电荷，通过车辆之间的吸引势能和排斥势能简化实际跟驰行为中对目标车辆的各种影响因素。因此，影响车辆的交通因素可以简化为车辆之间的相互吸引力和斥力，可以从一个新的角度研究车辆的跟驰行为。然而，随着网联自主车辆的出现，车辆的跟驰特性需要再认识，其中，文献[9]中提出的智能驾驶员模型(Intelligent Driver Model，IDM)可以完成传统车辆跟驰模型和自主车辆跟驰模型之间的转换；华雪东等[10]基于Newell跟驰模型建立了考虑车与车互联通讯技术的单车道跟驰模型；吴兵等[11]在传统车辆纵向控制模型(LCM)的基础上考虑车-车通讯环境下多辆前车运行信息，构建了智能网联环境下的C-LCM 模型，该模型能够刻画不同车辆的跟驰特点；加州大学伯克利分校PATH 实验室长期研究网联自主车辆的跟驰策略，并通过小规模的实车进行验证，但其目前较多的集中于车间时距跟驰策略，对其他策略的研究较少，秦严严等[12]对此类方法进行了综述。

综上所述，虽然有不少研究将势场理论应用于交通流领域，但以智能网联环境为背景的研究较少；而对于网联环境下的车辆跟驰，学者更多进行的是传统车辆跟驰模型在网联自主车辆上的适用性研究。因此，本文考虑在智能网联环境下，自主车辆具有通过自身传感器识别车道线和道路边界以及通过通讯功能实时获取前车加速度信息的特点，构建包含车道线势场、道路边界势场以及车辆作用势场的动态安全势场，基于该安全势场建立跟驰模型来描述CAV 的微观跟驰行为，并与具有代表性的IDM 和VTH 模型进行仿真对比，评估所建模型的有效性。

1 势场描述与建模

1.1 安全势场描述

从物理学的角度，场为具有特定属性的物体在非表面接触的情况下会对其周围一定空间范围内的其他物体产生相互作用力，相互作用力的大小随物体间相对位置的不同存在差异，而物体间由于具有了相互作用力也就具有了与相对位置有关的势能，因而，可将势场作为对物体周围整个空间内相互作用能力的一种描述。同样，在交通系统中也存在类似于上述的物理场，车辆在行驶过程中既不过于接近又不远离前车的行为可看作是车辆在受到前车势场中的作用力下不断通过加、减速寻求跟驰平衡点的过程。在智能网联环境下，CAV在未来得以普及，车辆的驾驶权由人工转移至车辆自主决策，每个影响车辆行驶的因素在其空间上都可以看作一个场源，安全势场则由这些场源势场的叠加，因此，安全势场可认为是反映交通因素对行车安全影响的物理场。

1.2 安全势场模型建立

CAV 在行驶过程中除了通过传感器感知周围其他车辆，还要感知车道线和道路边界线等其他交通因素，简单道路环境中的安全势场由车道线势场、道路边界势场和车辆作用势场这3 部分组成，分别用UL、UR和UV表示。CAV 的安全行驶是受到两侧车道线、道路边界和相邻车辆的虚拟合力的结果。

1.2.1 车道线势场

假设在简单的道路环境中，有两种道路标线。一种是车道分界线，用于分隔同一方向行驶的车辆；另一种是车向分界线，将不同方向行驶的车辆分开。简化的车辆行驶环境如图1所示。

图1 简化的车辆行驶环境Fig.1 Simplified environment of vehicle driving

两种类型的分界线共同对车辆的横向运动行为产生约束，使车辆尽可能地维持在车道中央行驶，GUNAY[13]的研究表明，车辆在车道内横向方向的位置呈正态分布，这种现象也可从势场的角度很好地解释。多车道车辆横向位置分布如图2所示。

图2 多车道车辆横向位置分布Fig.2 Distribution of vehicles across carriageway

规定道路最左侧车道线所在位置为x轴的原点。使用类高斯函数表示车道线势场分布，即

式中：N为道路横截面车道线数量；x为任意一点的横坐标；Pl为不同类型车道线势场的强度系数，用于确定车道线场强的最大峰值；l为道路线类型，其中，l=1 为白虚线，l=2 为双黄线，且P1≪P2；xi为第i条道路线的横坐标位置；δ为确定道路边界势场升降的速度，与车道宽度成正比。

1.2.2 道路边界势场

道路边界形成的势场相对于其他静态势场对行驶车辆具有更高的约束作用，并随着车辆的不断接近趋于无穷大，其目的在于严重警示CAV 偏离正常行驶方向，防止车辆过度靠近，以减小碰撞甚至冲出道路的风险。这种风险不会随着车辆的接近而线性增加，而是随着距离的缩短，安全风险会迅速增加。本文假定道路边界排斥力势场的形式为

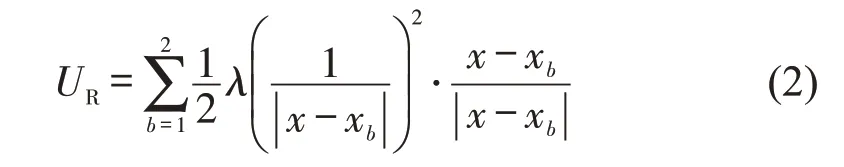
式中：b为道路边界线，规定b=1 为左边界，b=2为右边界；xb为道路边界线的横坐标；λ为位置增益参数。

参考文献[14]，设定P1=2，P2=8，δ=1.22，λ=3，根据式(1)和式(2)，绘制车道线场和道路边界场的分布情况，如图3所示，以及叠加后形成的三维势场，如图4所示。

图3 车道线和道路边界势场分布Fig.3 Potential field distribution of lane line and road boundary

图4 各类势场叠加示意图Fig.4 Superlay diagram of various potential fields

图4中只包含车道线势场和道路边界势场，不包含车辆以及其他交通设施或障碍物。由图可知不同车道线以及道路边界势场强度的大小对比，道路边界势场强度远大于白虚线的车道线势场，并随着距离的增加而减小；三者的合势场强度在车道线和道路边界所在的x轴的位置处达到峰值，并沿x轴方向在车道中央位置减小至最低。行驶中的车辆为保证安全，即使发生变道行为，也会使自己尽可能地处于势场的较低位置进行，以此减小安全风险。

1.2.3 车辆作用势场

车辆作用势场来源于道路上的车辆，文献[15]借用人工势场法的思想研究CAV 跟驰行为，人工势场包括引力场和斥力场，最初被用于机器人路径规划，其中目标点对物体产生引力，引导物体朝向其运动，障碍物对物体产生斥力，避免物体与之发生碰撞，但文中选用的引力函数和斥力函数是各自独立且割裂的，且在远距离的情况下容易出现引力过大的情况，因此，选择统一且合适的车辆作用势场函数尤为重要。

将在道路上的车辆微化到分子，分子之间合力的零点距离称为平衡距离r0，此时分子间势能最小，如图5所示。图中，r为分子间距离，rz为分子间引力最大时的间距，分别表示分子间作用力和势能。

图5 分子间作用关系与车辆跟驰行为关系对比Fig.5 Comparison between intermolecular interaction and car-following behavior

跟驰车辆间也存在着一种跟驰平衡距离，即车辆需求安全距离。车辆间距小于需求安全距离，受到前车的短程斥力；实际间距大于需求安全距离，受到前车的远程引力。从力学角度分析，行驶车辆的状态变化是在周边车辆引力与斥力共同作用下的运动，行驶车辆之间既不远离也不过近的特点与分子间的合力运动行为具有相似性，文献[16]基于分子之间的Lennard-Jones势建立的跟驰模型为

YANAKIEV 等[17]认为车辆需求安全间距不仅与当前车辆速度有关，也与前、后两车之间的速度差有关，根据其建立的VTH 跟驰策略可计算需求安全距离Xr为

式中：vn为跟驰车辆n的速度；t0、cv为待标定系数且大于0；vr为前、后车的相对速度。

上述跟驰模型都是基于分子动力学建模中被广泛使用的Lennard-Jones 6-12 势函数，简称6-12势[18]，即

式中：ε为能量尺度；为斥力项，即分子间的短程斥力；为引力项，即分子间的远程引力；当r很大时，分子间的引力接近于0。

在Lennard-Jones势模型中，势场中分子受到的相互作用合力f与势函数的关系为

由此可得

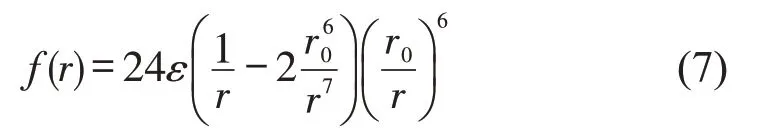
值得注意的是，6-12势仅是Lennard-Jones势的一种特殊标定形式，其引力项与斥力项的幂数的标定依据是流体中的微观粒子及其之间的相互作用。在车辆跟驰行为的场景中，相互作用的两物体无论在质量、速度还是加速度上，其数量级与粒子存在较大差异。因此，简单地将6-12势应用于现实中的车辆跟驰行为，会使跟驰车辆对前方车辆的速度以及车间距变化极为敏感，需要对其进行改进。

Lennard-Jones势原始的基本框架[19]为

式中：A、B为势函数关于r的中介变量；v、u分别为斥力项与引力项的幂次。

根据图5中势函数与距离之间的关系可得

联立式(8)～式(10)可得

将斥力项与引力项的幂次v与u设置为模型待标定的参数，构建车辆相互作用势场函数为

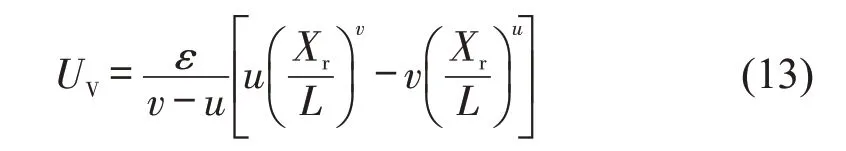
对车辆间相互作用势进行位移求导，得到跟驰车辆受力为

设车辆质量为M，简化模型，令，并考虑相邻两车的相对速度，得到由车辆作用势场产生的跟驰加速度表达式为

由式(15)可以看出，此势场仅考虑相邻前、后车辆之间的车间距和相对速度对本车加速度产生的影响，更多的适用于传统交通场景中，而对于智能网联环境，CAV基于通讯和传感技术还可以实时获取通信范围内前方多辆车的加速度信息，车辆n的加速度将由紧邻前车n+1 和非相邻前车i，共同影响决定，如图6所示。

图6 CAV跟驰场景示意图Fig.6 Schematic diagram of car-following scene of CAVs

因此，引入前车加速度的车辆需求安全距离可表示为

在势场平面上，任意一点的势场强度都与目标车辆的距离有关。在需求安全距离范围内，强度随着距离的减小而增大，并在目标车辆位置处达到最大值，如图7所示。

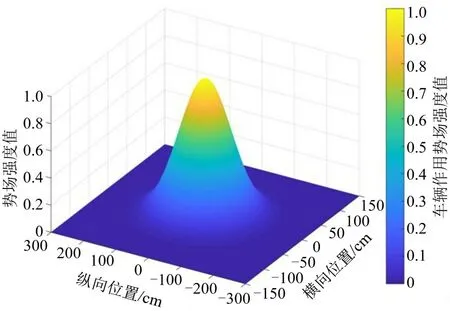
图7 单个车辆产生的势场分布Fig.7 Distribution of potential field generated by one vehicle

车辆处于不同运行状态会对其作用势场的分布产生不同的影响，除受车辆间的相对位置影响外，当前车辆的速度和加速度也是影响作用势场分布的主要因素。一方面，考虑到车辆侧身方向几乎不产生速度分量，车速的变化并不显著改变车身侧向的安全风险；另一方面，为保证车辆在停车静止时仍能够与前车保持最小的需求安全距离s0避免发生碰撞，修正后的短程斥力势场分布范围可表示为

式中：车辆的行驶方向为y轴；与车辆行驶方向垂直的为x轴；γ为待定系数；s0为停车最小安全距离。

因此，本文构建考虑车辆运动状态参数的车辆作用势场模型为

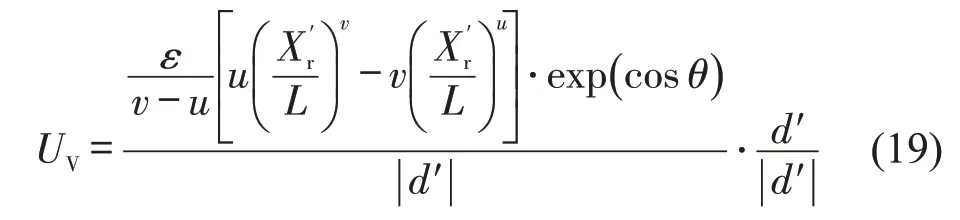
式中：θ为围绕目标车辆的任意点到目标车辆质心与车辆运动方向形成的顺时针夹角。

下面通过对短程斥力，即需求安全距离范围内的势场进行等高线投影分析车辆的作用势场特征，如图8所示。

(1)当目标车辆处于静止状态时，如图8(a)所示，该场景中车辆作用势场的等高线投影由几个同心圆组成，意味着在相同的距离内，不管另一辆车接近目标车辆的角度如何，其安全风险是相同的。在这种情况下，车辆可视为障碍物。

(2)当目标车辆沿y轴以恒定速度v=20 m⋅s-1移动，如图8(b)所示。与图8(a)相比，无论车辆在y轴方向上的速度如何变化，其在x轴方向上的势场强度和排斥力范围保持不变，原因在于车辆在x轴方向的速度分量仍为0；相反，车辆短程排斥力范围随目标车辆在y轴方向速度的增大而增大，势场强度沿车辆前、后方向梯度对称减小。在此情况下，车辆作用势的等高线投影由几个同心椭圆组成。

图8 车辆不同行驶状态下的短程斥力势场分布Fig.8 Short-range repulsive potential field distribution of vehicle under different driving states

(3)当目标车辆沿y轴进行加速度为1 m∙s-2的加速和减速运动，分别如图8(c)、(d)所示。在这两种情况下，即使车辆的速度在此时与图8(b)一致，但车辆前、后的短程排斥力范围和势场分布与匀速状态下的情况有明显的不同，这两种情况下的车辆势场分布明显分别向前方和后方倾斜。

通过以上分析，得出由车道线势场UL、道路边界势场UR和车辆作用势场UV构成的安全势场U能够动态地描述CAV在行驶过程中面临的安全风险，最终，车辆的安全势场模型可表示为

2 安全势场跟驰模型

车辆可以根据其周围交通环境的总势场分布确定其微观运动行为。车辆的微观运动行为主要体现在跟驰与换道两个方面。目前，CAV仍旧要以保证车辆行驶安全为首要条件，即CAV 跟驰要在各类势场的约束下，尽量寻求总势场的较低点，即低安全风险处进行行驶，如图9所示，圆点为车辆质心。

图9 安全势场下的车辆跟驰示意图Fig.9 Diagrammatic sketch of car following under safety field

由于可将车辆跟驰看作在各种场力作用下的运动，因此，跟驰车辆受到的合力可由U对位移求导获得，进而得出本文基于安全势场的跟驰模型(Safety Potential Field，SPF)表达式为

3 模型参数标定

3.1 数据准备

车辆的加速度信息不再简单地通过车载设备来检测，而是应用车-车无线通信技术，然而，目前多为单智能车独立运行，尚不具备车智能网联环境，在传统的环境中，虽然驾驶员无法获得前车运动信息的具体值，但基本也能对前车的速度变化做出及时响应，因此，选用更符合国人驾驶行为习惯的上海自然驾驶数据集[20]，该数据集来源于中国首个“上海自然驾驶研究”项目，项目采集了超过60人、行驶里程累计超过16 万km 的驾驶行为数据，通过SHRP2 NextGen 数据采集系统连接试验车辆的总线以及安装的3 轴加速度计、摄像机、雷达和GPS 获取车辆运行的高精度数据信息。系统的采样频率分布在10～50 Hz。数据提取流程如图10所示，相关规则为：

图10 有效跟驰片段提取流程Fig.10 Extractive process of effective car following segment

(1)判断前车D>0，即保证试验车雷达范围内存在前车；

(2)纵向车身间距S<150 m，即剔除试验车辆处于自由流情形的数据；

(3)跟驰持续时间T>20 s，即车辆在一个跟驰片段中所持续的最小时间，目的是提取多种变速状态下的车辆运行数据。

基于以上规则提取了30位驾驶人的1600个跟驰片段，经过人工较对，最后，提取有效片段1560个，其中，随机选择1040 个和520 个片段分别作为标定集和验证集。

3.2 算法选择

参数标定的算法有多种，包括：牛顿下山法、蚁群法和遗传算法。由于遗传算法具有高鲁棒性，能够适用多参数条件下快速求解，并且不易陷入局部最优等特点，故本文使用此算法进行标定。选择车速和车身间距对模型参数进行标定，采用均方根百分比误差(Root Mean Square Percentage Errors,RMSPE)作为目标函数衡量实测值与仿真值之间的偏差，表达式为

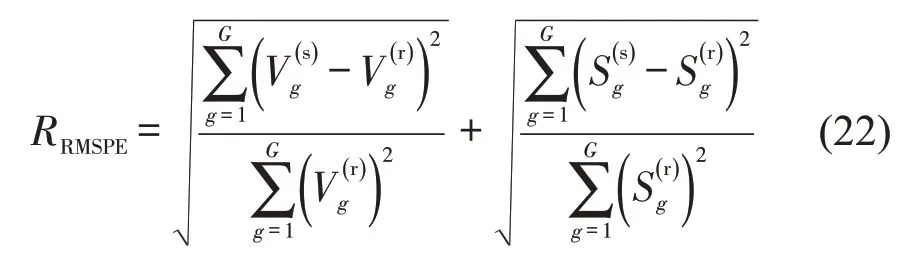
式中：G为总样本数；g为样本序号；分别为第g个样本的仿真速度和实际速度；分别为第g个样本的仿真车身间距和实际车身间距。

3.3 标定结果

使用Matlab中的遗传算法工具箱进行求解，将种群规模设置为400，最大遗传代数设置为300，截止代数设置为100，收敛容许误差设置为10-6，每次标定重复5次，取误差最小的一次作为参数标定的结果，如表1所示。

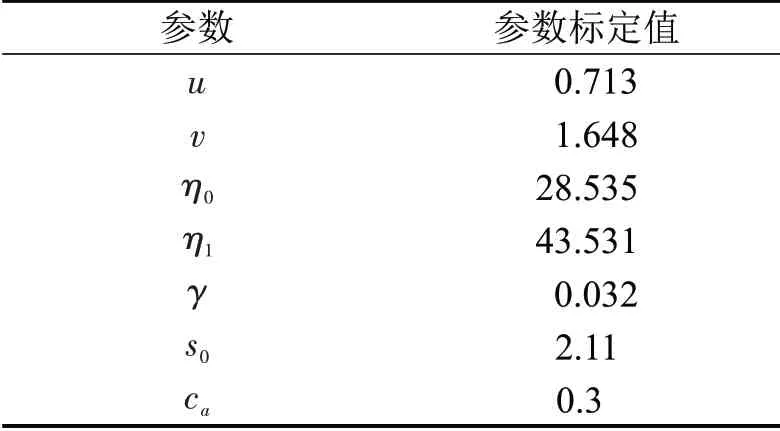
表1 模型参数标定结果Table 1 Calibrated results of parameters in model

4 模型效果评价

4.1 车道线和道路边界势场模型评价

为评价车道线势场和道路边界势场对车辆行驶过程中的约束效果,设置汽车初始位置距离车道中心线0.9 m，初始航向角为0°，仿真工况如图11所示。

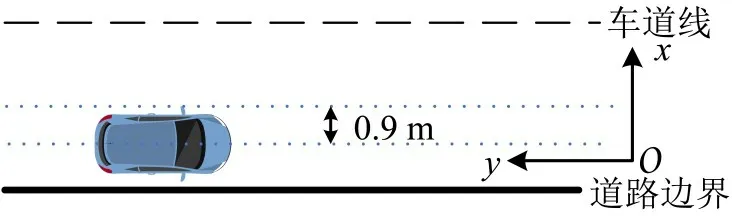
图11 车辆仿真初始工况示意Fig.11 Schematic diagram of initial working condition of vehicle simulation

仿真中采用线性二自由度车辆动力学模型，设置车辆前轮转角的约束范围为(-25°，25°)，路面附着系数为0.8，重力加速度取9.8 m∙s-2，仿真车速为25 m∙s-1，采样周期为0.05 s，车辆参数设置如表2所示。仿真结果如图12所示。

表2 车辆参数Table 2 Vehicle parameters

由图12(a)、(b)可知，车辆在6 s 左右时的侧向位移偏差和航向角偏差趋向于0，表明车道线和道路边界势场具有快速修复横向偏差的能力；同时，从图12(c)可知，车辆前轮的最大转角为0.22 rad，符合车辆自身转向范围的约束。为了进一步从宏观车流运行规律上评价车道线和道路边界势场的约束效果，在单向3 车道内分别进行多次仿真，获取每个车道内的370 辆车的运行轨迹并绘制频率直方图，结果显示，车辆在车道居中行驶的效果较为显著，满足车辆横向的安全需求，验证了车道线和道路边界势场具有良好的横向约束效果。车辆横向位置分布如图13所示。

图12 车辆初始工况下横向位置变化仿真结果Fig.12 Simulation results of lateral position change under initial working condition of vehicle

图13 车辆横向位置分布直方图Fig.13 Histogram of vehicle's lateral position distribution

4.2 跟驰模型评价

为了评价本文所建跟驰模型的效果，选择与IDM 和VTH 模型进行对比，原因在于IDM 含有反映车间时距这一物理意义的参数，能够与前车保持稳定的车间时距；VTH 是一种可变车头时距的跟驰策略，该策略下的车头时距除了与本车速度有关，还与前车速度有关。

IDM跟驰模型公式为

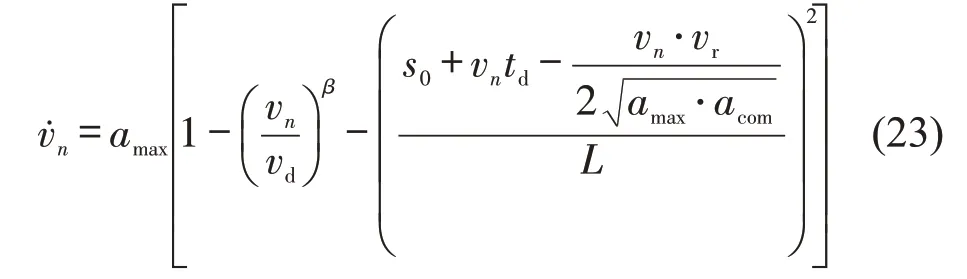
式中：amax为车辆最大加速度；vd为驾驶员的期望速度，即自由流速度；β为速度幂系数；td为跟车时距；acom为舒适减速度。

VTH跟驰模型为

采用同样的标定数据集和算法对IDM和VTH模型的参数进行标定，结果如表3所示。

表3 IDM和VTH模型参数标定结果Table 3 Result of parameter calibration of IDM and VTH model

为了有效评价3 种模型在车辆不同运行状态下的表现，在ζi=0 的条件下，选取前车频繁变速，远距离接近前车和前车急刹车的典型场景进行仿真，比较分析在不同交通状态下跟驰车辆的动态性能，验证所建模型的有效性。

(1)前车频繁变速场景下，仿真初始车头间距设为80 m，前、后车初始速度分别为31 m⋅s-1和26 m⋅s-1，整个过程使前车进行一定程度的加、减速，在不同跟驰模型下得到的跟驰车辆响应曲线如图14所示。

图14 前车频繁变速场景下不同模型的响应曲线Fig.14 Response curves of different models in scene of frequent speed changes of preceding vehicle

由仿真结果可知，在3 种模型下，后车为追赶前车在起始阶段均进行了相应地加速，但伴随前车的减速，跟驰车不得不采取减速以适应前车，从图14(a)可以看出，SPF 模型由于考虑了前车的加速度，在获取前车加速度为负时，其需求安全距离相对于IDM和VTH模型更大，并且在t=3.6 s 时最先进行减速，以避免与前车发生碰撞；而在IDM 和VTH 模型下，跟驰车分别在t=5 s 和t=4 s 开始进行减速，如图14(c)所示。另外，从图14(d)最大减速度可以看出，减速响应的滞后使其后续产生更剧烈的减速现象。随着时间推移，前车在t=7 s 时开始加速，其所受后车威胁减小。与此同时，在SPF 模型下，后车在获取前车的加速度为正时，其需求安全距离会在保证安全的前提下适当地减小，在t=8.4 s 时最先开始加速；而在IDM 和VTH 模型下，跟驰车分别在t=9.3 s 和t=8.8 s 逐渐开始加速，同样出现加速响应滞后使后续产生更为剧烈的加速现象。综上所述，在常规跟车场景下，SPF 模型具有更好的适应性和预见性，能够更好地在前车减速时通过增加需求安全距离保证跟车安全，在前车加速时通过适当减小需求安全距离提高跟车效率。

(2)远距离接近前车的场景下，前后车的初始速度设为20 m∙s-1，初始间距设为120 m，整个过程中前车先匀速再减速行驶，得到3种模型下的跟驰车辆响应曲线如图15所示。

图15 远距离跟驰场景下不同模型的响应曲线Fig.15 Response curves of different models in scene of long distance car following

由仿真结果可知：SPF模型下跟驰车辆在起始阶段受到的是前车的远程吸引力，和其他两种模型一样采取了较大的加速度靠近前车，同时，需求安全距离随速度的增大而增大。当前车速度减小时，SPF模型下的跟驰车及时获取这一变化信息，需求安全距离变得更大，使受到前车的远程吸引力迅速变为短程排斥力，并最先在t=3.2 s 时进行减速；而IDM 和VTH 模型未能精确感知这一变化，分别在t=4.5 s 和t=3.7 s 时进行减速，如图12(c)所示，响应的滞后导致其后续速度的变化即加速度变得更为剧烈，如图12(d)所示。在整个靠近过程中可以看出，SPF 模型能够及时地响应前车的速度变化，使自身速度变化更为平缓，提高了行驶的安全性。

(3)前车急刹车的场景能够最大程度地检验模型的行驶安全性。前、后车的初始速度都设为20 m∙s-1，初始车头间距设为60 m，在t=5 s 时使前车进行急刹车，速度迅速减至为0，在此情况下各模型的响应曲线如图16所示。

由仿真结果可知：前车在t=5 s 时进行了急刹车，其后向短程排斥力形成的安全势场范围迅速变大，SPF 模型下的跟驰车由于考虑了前车的加速度，在t=5 s 时及时获取前方车辆加速度变化信息，立即通过增加其自身需求安全距离并及时地进行制动，避免了与前车发生碰撞；而IDM和VTH模型下的跟驰车均在t=20 s 以后与前车发生了碰撞(实际车头间距<车身长度5 m)，如图16(b)所示，证明了在该场景下SPF 模型能够更有效地提高跟驰车辆的行驶安全性。

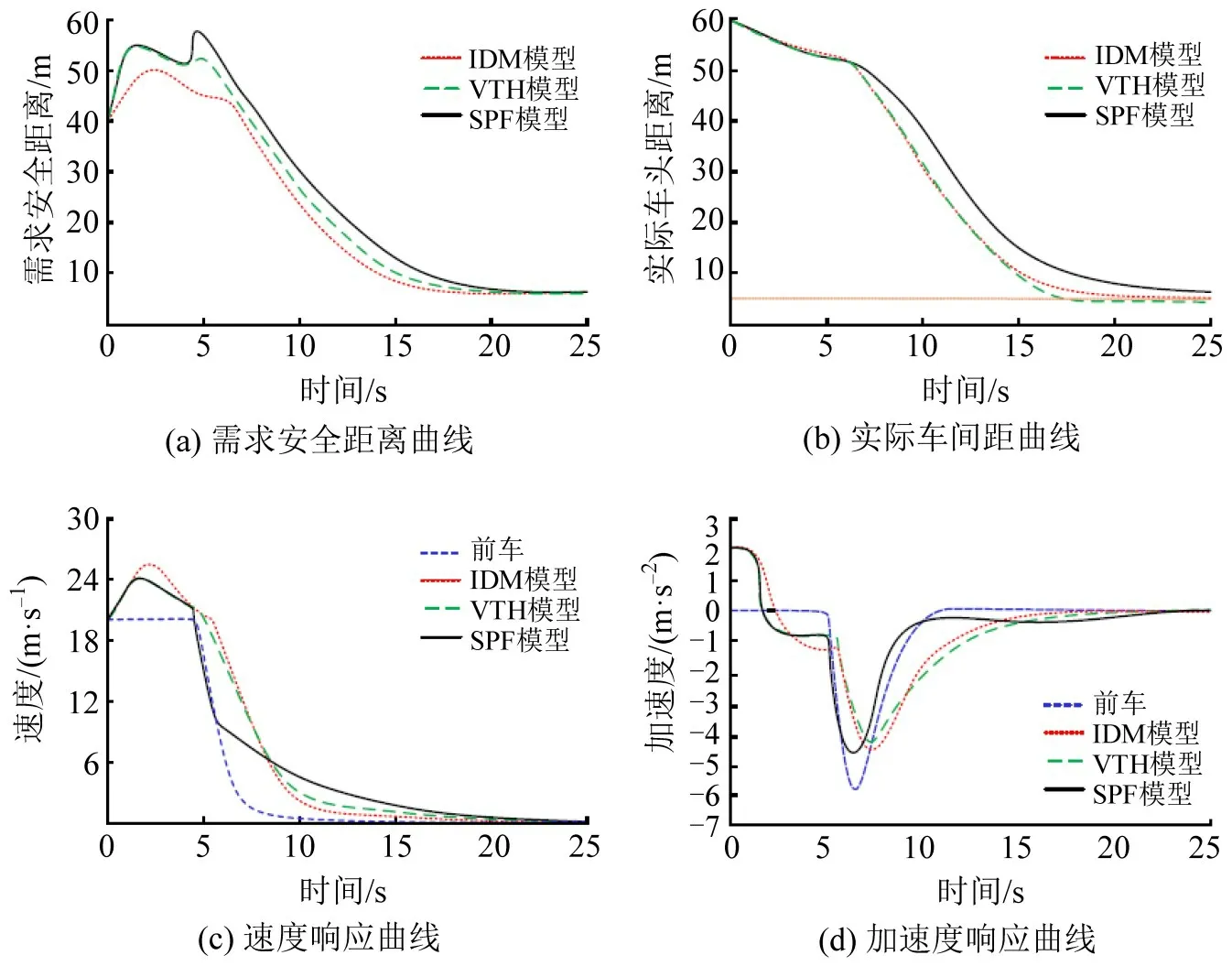
图16 前车急刹车场景下不同模型的响应曲线Fig.16 Response curves of different models in scene of preceding vehicle emergency braking

为评价3 种模型在车队中的表现，在ζi=1，σi=0.1 的条件下搭建由5辆车组成的车队，选择首车在减速和加速的场景下进行仿真。场景1，5 辆车在高速公路单车道上以车队的形式行驶，初始速度设置为20 m∙s-1，车头间距为32 m，在t为0 时，首车制动并逐渐减速为0。场景2，10 辆车以20 m∙s-1的速度在高速公路单车道上以车队的形式运行，车头间距为20 m，首车从t为0开始加速至最高速度33 m∙s-1之后，保持匀速，后车根据跟驰模型随前车减速做出响应的曲线如图17所示，加速做出响应的曲线如图18所示。

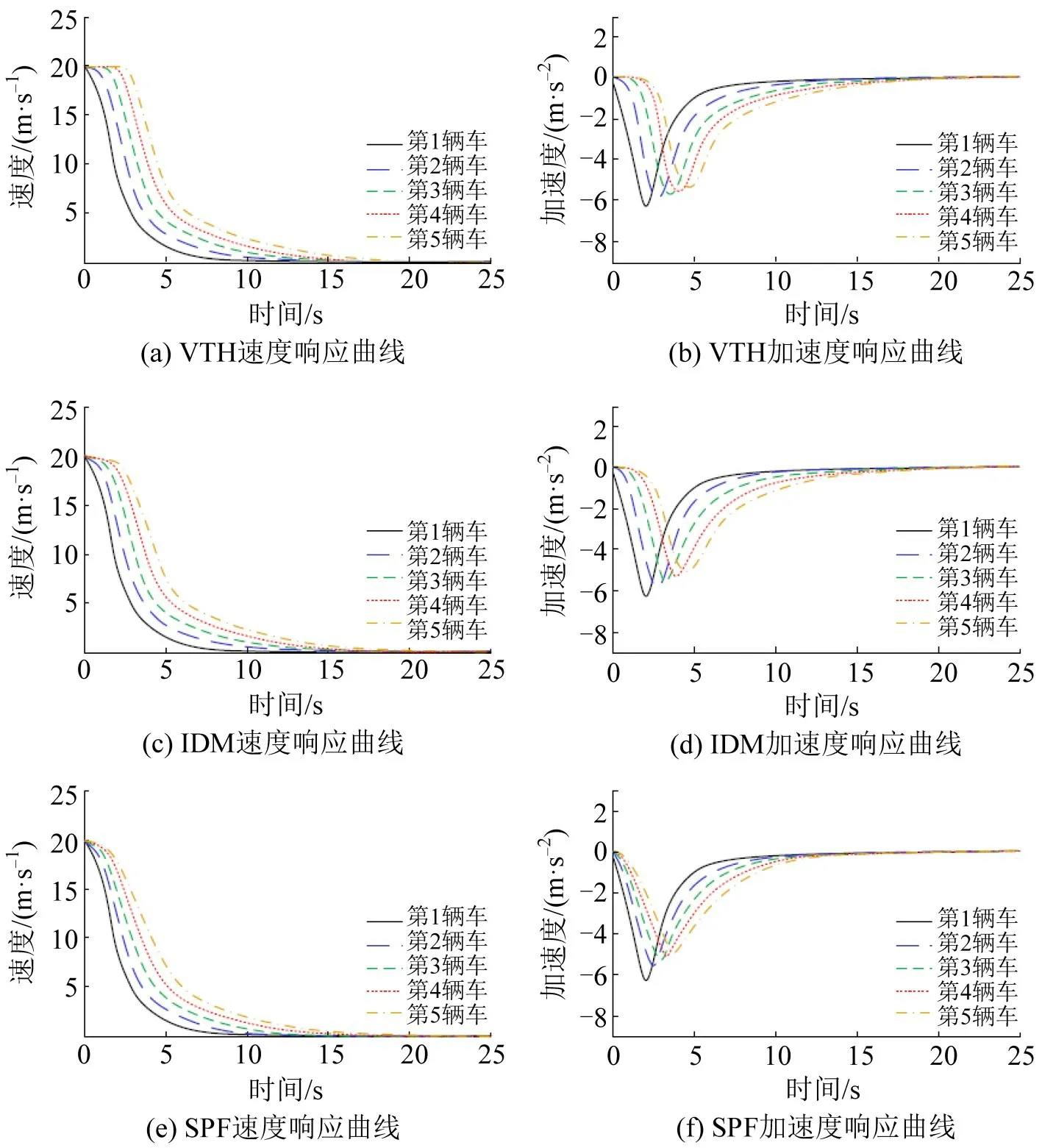
图17 车队首车减速情景下不同模型的响应曲线Fig.17 Response curves of different models under deceleration of first vehicle in fleet

由仿真结果可知：在VTH模型下，尾车在首车减速和加速两种情景下的响应曲线具有最大的延迟性；在IDM模型下，后方车辆虽然能对前车的减速行为及时做出响应，但车辆只与紧邻的前车有关，致使尾车对首车的响应存在一定的延迟；相比而言，在SPF模型下，当第1辆车减速时，其行为会立即作用到后面全部车辆，尾车可以更快地对首车的行为做出反应。与此同时，从图17可以看出，在整个减速过程中，SPF模型下的加速度变化幅度也相对更小，有利于提高乘车的舒适性，从图18可以看出，在整个加速过程中，尾车也可以更快地达到首车的速度进而进行匀速行驶，提高了车队整体的运行效率。