单颗粒煤粉着火特性的数值分析

张廷尧，胡中发，周月桂

单颗粒煤粉着火特性的数值分析

张廷尧，胡中发，周月桂

(上海交通大学机械与动力工程学院热能工程研究所，上海 200240)

建立了模拟静止的单颗粒煤粉着火燃烧过程的气相和固相耦合的质量、组分和能量守恒方程组，采用不同脱挥发分模型研究了不同热力氛围下单颗粒煤粉的着火延迟时间和着火模式等特性．基于热力着火理论的煤粉异相着火和均相着火判据，确定了不同热力氛围下煤粉颗粒发生着火模式转变的临界参数．结果表明，采用化学渗透脱挥发分(CPD)模型预报的煤粉着火延迟时间比双挥发反应模型更加准确．在21%的氧气体积分数下，环境温度为1500K时，煤粉着火模式发生转变的临界粒径为150μm；环境温度为1100K时，其临界粒径为300μm.

单颗粒煤粉；CPD模型；着火延迟时间；着火模式；临界粒径

煤粉的着火特性是煤粉燃烧系统工程设计中的一个重要参数，改善煤粉的着火特性有助于提高燃烧效率和降低污染物的排放．煤粉着火和燃烧是一个包含脱挥发分、挥发分燃烧、焦炭氧化和气化等反应的复杂过程．许多研究表明，煤粉的初次着火可以是由挥发分着火引起的均相着火，也可以是由煤粉颗粒表面反应主导的异相着火[1-3]．在均相着火模式下，热解释放的挥发分先发生着火，随后挥发分在类似油滴的气相火焰中燃烧，煤粉颗粒表面的氧气体积分数很低甚至为零，导致焦炭的氧化反应停止．在异相着火模式下，氧气直接与固体颗粒接触并发生反应，这个固体颗粒不仅仅是焦炭，而是整个煤粉颗粒，异相反应会消耗本可以以气相挥发分形式析出的物质[4].煤粉的着火模式与煤粉颗粒的煤种、粒径、加热速率、环境氛围的温度、氧气的体积分数以及燃烧氛围等有关．

如何建立气相与固相耦合的数学模型对煤粉颗粒的着火燃烧过程进行理论分析是一个研究的热点和难点．文献[5-7]分别建立了基于稳态、准稳态和瞬态等假设的煤粉颗粒着火燃烧模型．其中稳态和准稳态的模型假设在煤粉颗粒周围有足够的时间达到稳定状态，并在达到煤粉自着火温度下发生着火．然而在实际的煤粉炉中，煤粉颗粒的停留时间有限，炉内温度也远远高于煤粉的自着火温度，因此建立瞬态的煤粉颗粒着火和燃烧模型更加合理[8]．煤粉的脱挥发分反应直接影响着煤粉颗粒的均相着火燃烧过程．随着煤粉脱挥发分模型的发展，复杂的脱挥发分模型已经可以用于解释煤的化学结构和脱挥发分过程中的变化[9]．20世纪70年代发展的阿伦尼乌斯形式的脱挥发分模型，如一步反应模型和双挥发反应模型在形式上比较简单，但需要通过实验获得对应煤种的动力学参数[10-11]．化学渗透脱挥发分CPD(chemi-cal percolation devolatilization)模型是目前能够精确预报煤粉脱挥发分过程的模型，它把煤粉颗粒视为大分子网络结构，考虑了不同煤种的结构变化，能够预报脱挥发分过程中轻质气体的释放过程[12]. Jovanovic等[9]通过数值模拟比较了利用4种不同复杂程度的脱挥发分模型获得的煤粉着火点的预测结果，结果表明CPD模型预报的结果与实验结果符合最好．

本文建立了瞬态的单颗粒煤粉着火燃烧模型，研究并比较了双挥发反应和CPD两种脱挥发分模型对煤粉着火延迟时间预报准确性的影响，发现CPD模型预报的煤粉着火延迟时间比双挥发反应模型更加准确．在此基础上，采用基于CPD的单颗粒煤粉着火燃烧模型，通过比较均相着火和异相着火延迟时间的长短定义了单颗粒煤粉的着火模式，研究了煤粉颗粒的粒径、环境氧气体积分数和温度对单颗粒煤粉的着火温度以及着火模式的影响，确定了着火模式转变的临界参数，研究结果对实际煤粉炉内煤粉着火的强化有重要意义．

1 单颗粒煤粉瞬态着火燃烧模型

1.1 瞬态模型假设

假设一个半径为的常温煤粉颗粒突然被放入高温空气中，煤粉颗粒被环境气体加热．随着煤粉颗粒温度的增加，脱挥发分反应开始，释放的挥发分组分和质量随加热速率、加热时间和煤粉颗粒温度的改变而改变．瞬态模型中涉及到以下假设：①煤粉颗粒球形对称，刘易斯数＝1；②煤粉颗粒干燥并且不考虑灰分；③煤粉颗粒与环境气体间没有相对移动；④煤粉颗粒的温度随时间变化，但内部温度分布均匀；⑤煤粉颗粒在脱挥发分过程中体积不发生变化，在表面异相反应过程中密度不发生变化而煤粉颗粒粒径减小；⑥焦炭的氧化反应是氧气的一级反应，反应产物为CO2；⑦煤粉颗粒周围的气体满足理想气体状态方程．

1.2 气相守恒方程

质量守恒方程

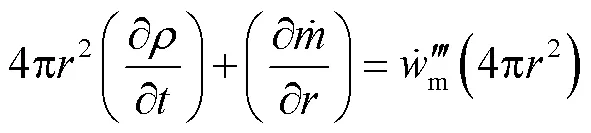
组分守恒方程

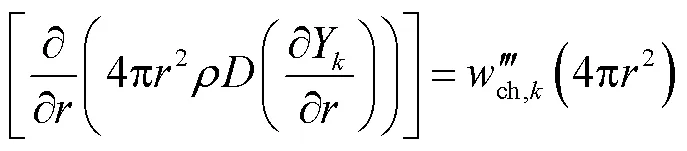
在过去的煤粉燃烧模拟研究中，经常采用火焰锋面模型来模拟气相燃烧反应[13-14]．为了解决该模型中假设化学反应无限快带来的限制，后来一些学者采用多步总包反应模型或详细化学反应模型来求解气相燃烧反应[15-16]．本文选用总包反应动力学来求解挥发分的燃烧过程：

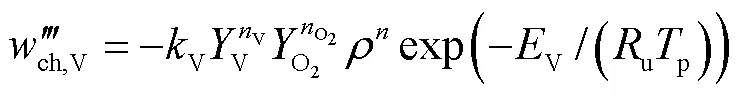
能量守恒方程

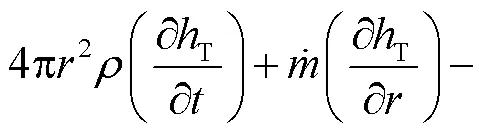
(4)

1.3 颗粒相方程

颗粒质量方程

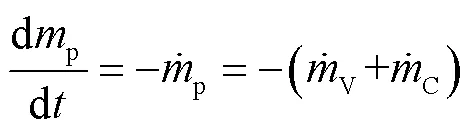
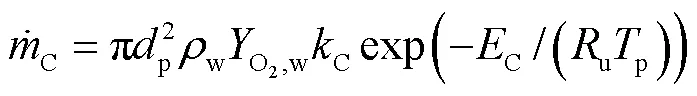
颗粒密度方程

颗粒半径方程

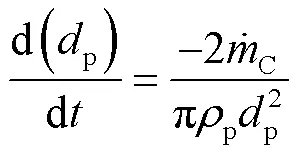
颗粒温度守恒方程

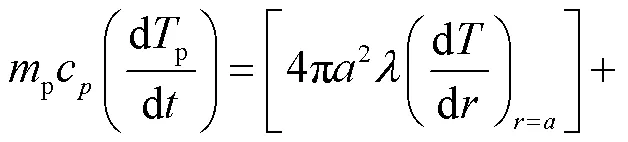
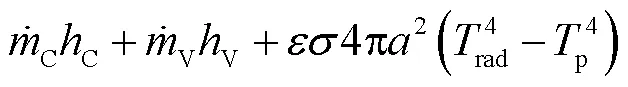
1.4 脱挥发分模型

脱挥发分反应是煤粉着火燃烧过程中一个重要的子过程，本文检验了两种不同复杂程度的脱挥发分模型对煤粉着火延迟时间预报的影响．

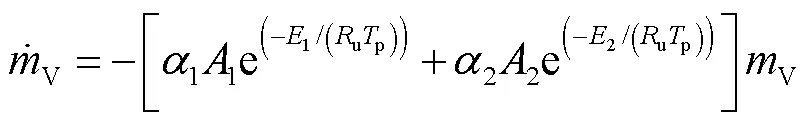
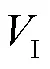
表1 Pittsburgh高挥发分烟煤双挥发反应动力学参数

Tab.1 Kobayashi-Sarofim devolatilization kinetic pa-rameters for high volatile Pittsburgh bituminous coal

CPD模型是目前预测煤粉脱挥发分过程中物质释放速率最精确的模型之一，它根据煤的化学结构来预测不同煤种的脱挥发分过程[12]．在CPD模型中，煤被描述为由不同大小和类型的芳香环簇组成的大分子网络，这些芳香环簇由不同化学键强度的化学桥(即“不稳定桥”)连接起来．脱挥发分过程从不稳定桥分解形成高反应性的中间桥l开始．这些中间桥进一步反应生成焦油(C2H2)和轻质气体(CO2，CO，CH4，H2O)或侧链，侧链可能最终会形成轻质  气体．

1.5 模拟计算过程

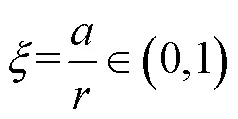
2 结果分析与讨论

2.1 脱挥发分模型对着火延迟时间预报准确性的影响

对美国典型Pittsburgh高挥发分烟煤的着火过程进行了模拟，该煤种的工业分析和元素分析见表2，空气氛围下煤粉着火延迟时间的实验数据来自文献[17].计算中设置煤粉颗粒的初始密度为1300kg/m3，初始温度为298K．根据谢苗诺夫(Semenov)热力着火理论，当产热率大于等于热损失率时发生着火，由此可以推导出煤粉颗粒的异相着火发生在煤粉颗粒温度随时间变化曲线的拐点(d2p/d2＝0，且dp/d＞0)．当煤粉颗粒周围的气相氛围中氧气和挥发分的浓度和温度到达了着火极限，就会发生均相着火．在模型计算中，当某一计算单元(内径为，外径为＋Δ的计算区域)的气相温度高于了相邻计算单元(内径为－Δ，外径为的计算单元和内径为＋Δ，外径为＋2Δ的计算单元)的气相温度的时候，即局部气相氛围中的氧化反应速率快速增加，认为在该时刻发生了均相着火．煤粉的着火延迟时间定义为均相着火延迟时间和异相着火延迟时间中最短的那个时间，煤粉的着火模式定义为初次发生着火的那种模式.

表2 Pittsburgh高挥发分烟煤工业分析和元素分析

Tab.2 Proximate and ultimate analysis for high volatile Pittsburgh bituminous coal

图1是利用CPD模型和双挥发反应模型计算得到的煤粉着火延迟时间与Shaddix等[17]实验结果的比较．利用瞬态的单颗粒煤粉着火燃烧模型预报的着火延迟时间与实验结果符合较好，验证了模型的准确性．利用两种脱挥发分模型计算得到的着火延迟时间都随氧气体积分数的增加而减少，CPD模型明显比双挥发反应模型预报的着火延迟时间更加准确，因此下文中均采用CPD模型计算的结果进行分析．在1700K的环境温度下，CPD模型预报的挥发分释放速率更快，析出的挥发分含量更高[7]，煤粉颗粒表面的可燃混合物更快达到着火极限，因此计算得到的着火延迟时间更短．在氧气体积分数为36%的工况下，利用两种脱挥发分模型预报的煤粉颗粒着火模式均为异相着火，这意味着在高的氧气体积分数下，焦炭的表面反应速率明显加快，煤粉颗粒首先发生异相着火．

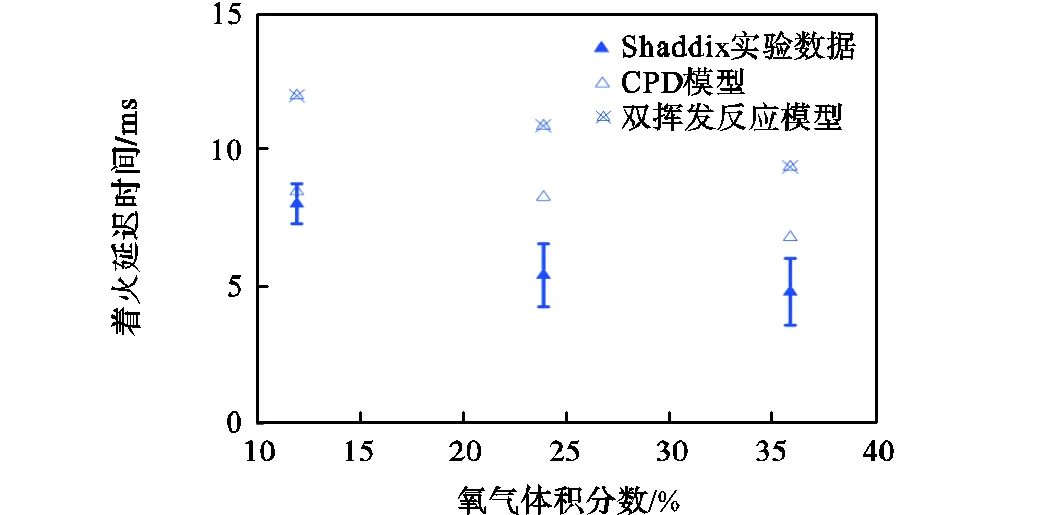
图1 不同环境氧气体积分数下的着火延迟时间

2.2 颗粒粒径对着火特性的影响

模型计算中记录了煤粉颗粒和周围气体的温度随时间的变化．当发生异相着火时，定义该时刻的煤粉颗粒的温度为异相着火温度(p,HI)．随着煤粉颗粒温度进一步增加，煤粉颗粒脱挥发分反应速率加快，颗粒周围的挥发分浓度逐渐升高并发生均相着火，气相氛围中会出现一个温度的峰值，定义这个温度的峰值为二次均相着火温度(g,SGI)．如果初次着火模式为均相着火，则定义发生均相着火的当地位置处的气体温度为均相着火温度(g,GI)．

图2给出了在环境温度1500K、氧气体积分数为21%时煤粉颗粒着火温度以及着火模式随粒径的变化．从图中可以看出，异相着火温度随粒径的增大而降低，二次均相着火的温度变化不大，煤粉颗粒的着火模式从异相着火转变为均相着火的临界粒径为150μm．由于煤粉在脱挥发分过程中释放的挥发分通量与粒径成正比，煤粉颗粒表面的气体的传质系数与粒径成反比，因此小的煤粉颗粒周围的挥发分浓度低，大的煤粉颗粒周围的挥发分浓度高．当颗粒粒径小于150μm时，煤粉颗粒周围的挥发分浓度比较低，难以发生均相着火．在煤粉颗粒受热升温的过程中，焦炭表面氧化反应速率逐渐增加，首先发生异相着火，随后煤粉颗粒温度迅速增加，导致脱挥发分反应速率也快速增加，煤粉颗粒周围的挥发分浓度达到着火极限时，发生二次均相着火．当粒径大于150μm时，煤粉颗粒周围的挥发分浓度足够高，首先发生均相着火．此时氧气在气相氛围中消耗殆尽，无法到达煤粉颗粒表面，直到脱挥发分过程结束后才会发生焦炭的二次着火．随着粒径的增加，煤粉颗粒表面外的挥发分浓度也随之增加，达到均相着火极限所需的气体温度逐渐降低，因此均相着火温度随粒径的增大而略有减小．由于大的煤粉颗粒的内部可能存在温度梯度，煤粉颗粒内部的温度低于颗粒表面的温度，实际的脱挥发分反应速率要小于在均匀煤粉颗粒温度假设下预测的速率，因此实际发生着火模式转变的临界粒径要大于150μm．

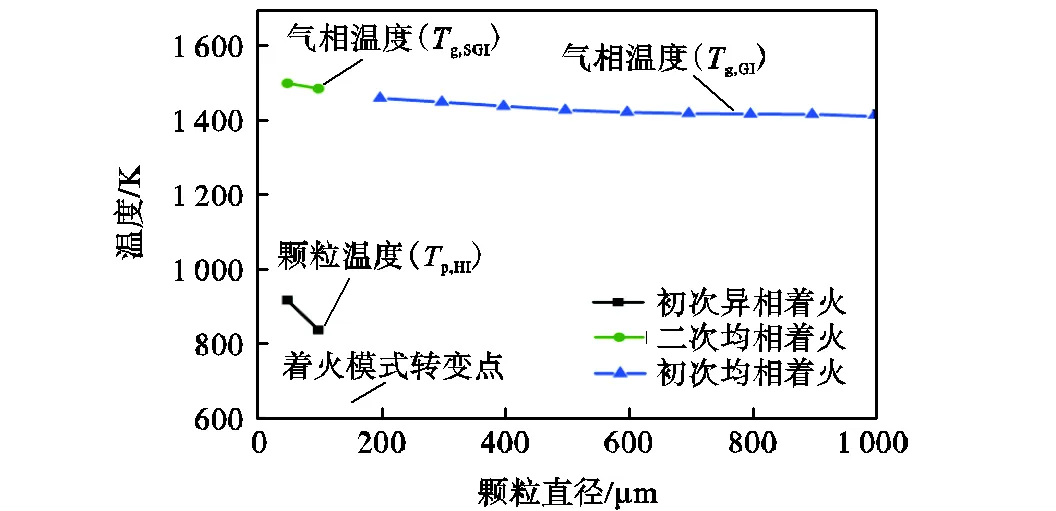
图2 不同煤粉粒径下着火温度的变化

2.3 环境温度对着火特性的影响

图3显示了不同粒径下环境温度对煤粉的着火温度以及着火模式的影响(环境氧气体积分数21%).当环境温度从1500K降低至1100K时，小的煤粉颗粒初次着火模式仍然为异相着火，大的煤粉颗粒初次着火模式也仍然为均相着火，但是着火模式从异相着火转变为均相着火的临界粒径从150μm增加到了300μm．这是由于随着环境温度的降低，气相燃烧反应速率变慢，因此需要在更大的粒径下产生更多的挥发分以达到着火极限．当环境温度降低到900K时，气体的温度低于挥发分的自着火温度，因此在所有粒径下均发生异相着火．从图中还可以发现，煤粉颗粒的异相着火温度不随环境温度的改变而发生变化，这意味着煤粉颗粒的异相着火温度只与焦炭的反应动力学和环境中的氧气体积分数有关．当环境温度进一步降低时，焦炭的氧化反应速率非常缓慢，煤粉颗粒既不会发生均相着火也不会发生异相着火．

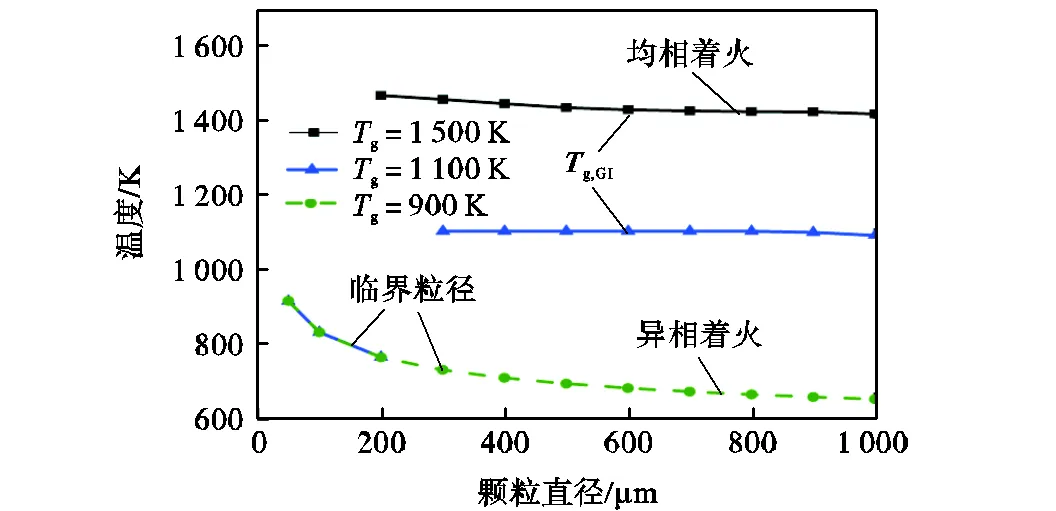
图3 不同环境温度下着火温度随粒径的变化

2.4 氧气体积分数对着火特性的影响

图4展示了不同粒径下氧气体积分数对煤粉颗粒的着火温度和着火模式的影响(环境温度1500K).从图中可以看出，在低氧气体积分数下，由于焦炭表面的氧化反应速率缓慢，总是先发生均相着火．随着氧气体积分数的增加，煤粉颗粒周围的挥发分更容易达到着火极限从而发生均相着火，因此均相着火温度逐渐降低．而在高氧气体积分数下，煤粉颗粒表面的氧气体积分数很高，并且氧气体积分数越高，焦炭表面的氧化反应速率越快，越容易发生异相着火，因此颗粒的异相着火温度也逐渐减小．着火模式从均相着火转变为异相着火的临界氧气体积分数随粒径的变化而发生改变．当粒径为100μm时，临界氧气体积分数为15%；当粒径为300μm时，临界氧气体积分数为21%；当粒径为600μm时，临界氧气体积分数为30%．

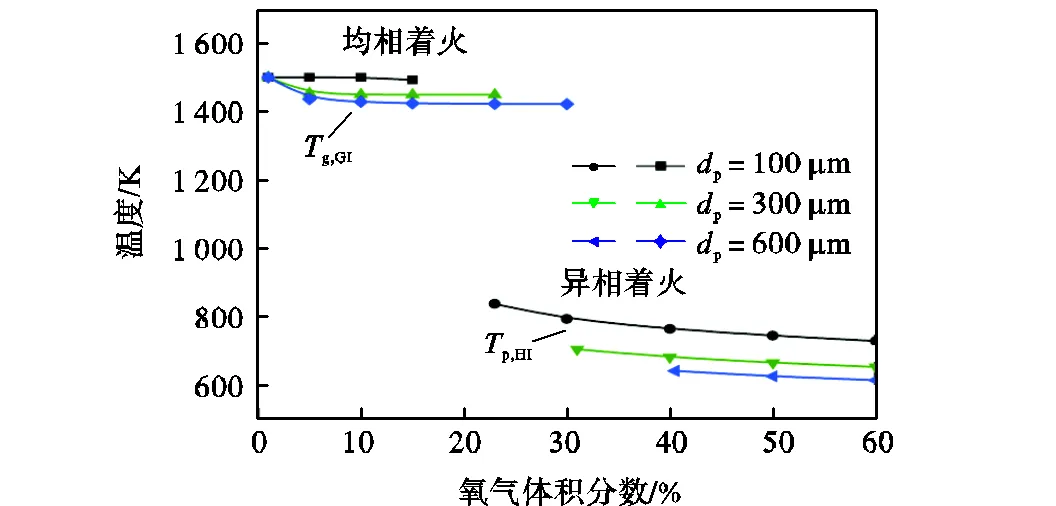
图4 不同氧气体积分数下着火温度的变化

3 结 论

建立了气相与固相耦合的瞬态单颗粒煤粉着火燃烧模型，模拟了美国典型的Pittsburgh高挥发分烟煤的着火特性，研究了煤粉颗粒的粒径、环境温度和氧气体积分数对煤粉颗粒的着火温度以及着火模式的影响．主要结论如下：

(1) 利用瞬态的单颗粒煤粉着火燃烧模型预报的煤粉着火延迟时间与实验结果符合较好．采用复杂的CPD模型比相对简单的双挥发反应模型预报的着火延迟时间更加准确．

(2) 小的煤粉颗粒容易发生异相着火，大的煤粉颗粒容易发生均相着火．在21%的氧气体积分数下，环境温度为1500K时，煤粉着火模式从异相着火转变为均相着火的临界粒径为150μm；环境温度为1100K时，其临界粒径为300μm．

(3) 煤粉颗粒的异相着火温度只与焦炭的反应动力学和环境氧气体积分数有关，并随颗粒粒径和氧气体积分数的增大而降低．煤粉颗粒的均相着火温度随氧气体积分数和粒径的增大略有减小．

符号说明：

——颗粒半径，m；

1——脱挥发分反应1指前因子，1/s；

2——脱挥发分反应2指前因子，1/s；

c——气体的比热，kJ/(kg·K)；

p——煤粉颗粒的直径，m；

——质量扩散系数，m2/s；

——刘易斯数；

p——煤粉颗粒的质量，kg；

V——未脱挥发分的煤粉颗粒的质量，kg；

u——通用气体常数，kJ/(kmol·K)；

——距离颗粒中心的径向距离，m；

——时间，s；

p——气体温度，K；

rad——辐射物体温度，K；

p,HI——初次异相着火时颗粒温度，K；

g,GI——初次均相着火时气体温度，K；

g,SGI——二次均相着火时气体温度，K；

［1］ Jüntgen H，Van Heek K H. An update of german non-isothermal coal pyrolysis work[J].，1979，2(4)：261-293.

［2］ Li Shuiqing，Xu Yang，Gao Qi. Measurements and modelling of oxy-fuel coal combustion[J].，2018，37：2643-2661.

［3］ 应 芝，郑晓园，崔国民. 基于O2/CO2气氛的煤粉燃烧性能研究[J]. 动力工程学报，2019，39(1)：7-12.

Ying Zhi，Zheng Xiaoyuan，Cui Guomin. Analysis on the combustion characteristics of pulverized coal under O2/CO2atmosphere[J].，2019，39(1)：7-12(in Chinese).

［4］ Essenhigh R H，Misra M K，Shaw D W. Ignition of coal particles：A review[J].，1989，77(1)：3-30.

［5］ Zhu Mingming，Zhang Hai，Zhang Zhezi，et al. A numerical modeling study of ignition of single coal particles under microgravity conditions[J].，2011，183(10-12)：1221-1235.

［6］ 金旭东，周月桂，金圻烨，等. CO2效应对煤焦颗粒增氧燃烧影响的数值研究[J]. 动力工程学报，2016，

36(12)：941-950.

Jin Xudong，Zhou Yuegui，Jin Qiye，et al. Influence of CO2effect on coal char combustion in oxygen-enriched environment[J].，2016，36(12)：941-950(in Chinese).

［7］ Goshayeshi B，Sutherland J C. A comparison of various models in predicting ignition delay in single-particle coal combustion[J].，2014，161(7)：1900-1910.

［8］ 袁梦帆，孙 锐，齐洪亮，等. 热解半焦颗粒携带流中着火特性的数值模拟[J]. 燃烧科学与技术，2021，27(6)：591-598.

Yuan Mengfan，Sun Rui，Qi Hongliang，et al. Numerical simulation of ignition characteristics of pyrolytic semi-coke particles in entrained flow[J].，2021，27(6)：591-598(in Chinese).

［9］ Jovanovic R，Milewska A，Swiatkowski A，et al. Sensitivity analysis of different devolatilization models on predicting ignition point position during pulverized coal combustion in O2/N2and O2/CO2atmospheres[J].，2012，101：23-37.

［10］ Badzioch S，Hawksley P G W. Kinetics of thermal decomposition of pulverized coal particles[J].，1970，9(4)：521-530.

［11］ Kobayashi H，Howard J B，Sarofim A F. Coal devolatilization at high temperatures[J].，1977，16(1)：411-425.

［12］ Fletcher T H. A review of 30 years of research using the CPD model[J].，2019，33(12)：12123-12153.

［13］ Lau C W，Niksa S. The combustion of individual particles of various coal types[J].，1992，90(1)：45-70.

［14］ Vascellari M，Xu H，Hasse C. Flamelet modeling of coal particle ignition[J].，2013，34(2)：2445-2452.

［15］ Xu Yang，Li Shuiqing，Gao Qi，et al. Characterization on ignition and volatile combustion of dispersed coal particle streams：In-situ diagnostics and transient modelling[J].，2018，32：9850-9858.

［16］ Tufano G L，Stein O T，Kronenburg A，et al. Fully-resolved simulations of coal particle combustion using a detailed multi-step approach for heterogeneous kinetics[J].，2019，240：75-83.

［17］ Shaddix C R，Molina A. Particle imaging of ignition and devolatilization of pulverized coal during oxy-fuel combustion[J].，2009，32(2)：2091-2098.

Numerical Analysis of the Ignition Characteristics of Single Coal Particle

Zhang Tingyao，Hu Zhongfa，Zhou Yuegui

(Institute of Thermal Energy Engineering，School of Mechanical Engineering，Shanghai Jiao Tong University，Shanghai 200240，China)

A transient model for the ignition and combustion process of a quiescent single coal particle was developed by coupling the mass, species and energy governing equations. Kobayashi-Sarofim devolatilization model and chemical percolation devolatilization(CPD)model were utilized to study the ignition characteristics of a single coal particle such as ignition delay time and ignition mode, respectively. The critical parameters for the transition of ignition mode of a single coal particle were determined by using the heterogenous and homogenous ignition criteria of a single coal particle based on thermal explosion theory under different ambient conditions. The simulated results show that CPD model performs better than Kobayashi-Sarofim devolatilization model in predicting the ignition delay time of a single coal particle. The critical coal particle size for the transition of ignition mode from heterogeneous to ignition is 150μm at the ambient gas temperature of 1500K and 300μm at 1100K with the oxygen volume fraction of 21%.

single coal particle；CPD model；ignition delay time；ignition mode；critical coal particle size

TK11

A

1006-8740(2022)01-0036-06

2021-03-17.

国家自然科学基金资助项目(51761125011；51976120；51576128).

张廷尧（1995—  ），男，博士研究生，tyzhang@sjtu.edu.cn.Email：m_bigm@tju.edu.cn

周月桂，男，博士，教授，ygzhou@sjtu.edu.cn.

(责任编辑：梁 霞)