考虑需求侧响应的园区综合能源系统优化配置

朱志芳，许 苑，岑海凤，黄文靖，郑杰辉，李志刚

（1.广东电网有限责任公司广州供电局，广东广州 510620；2.华南理工大学电力学院，广东广州 510641）

0 引言

在“碳达峰”、“碳中和”、新能源为主体的新型电力系统等国家能源政策背景下，可再生能源的迅速发展极大地提高了新能源在配电网中的渗透率，传统的单向功率流配电网逐渐演变为功率双向流动的主动配电网，隶属于配电网终端消费侧的园区综合能源系统（Park-Level Integrated Energy System，PIES）成为现阶段实现多能互补的规划建设重点。PIES 是集合了电、气、冷、热等能源形式的区域级综合能源系统，在能源综合利用、节能减排、可再生能源就地消纳等方面具有重要意义[1]。对于主动配电网来说，PIES 与配电网进行双向能量流动，具有“源”、“荷”双重特性[2-3]。然而，随着大量实践的展开，部分PIES 在运营中存在部分设备长期闲置而部分设备容量紧缺的问题[4]，造成经济损失的同时还削弱了能源间相互转化的能力，降低了PIES 的用能效率。

现有的PIES 一般可接入区域配电网及天然气网，还可以充分利用太阳能、风能、生物质能等区域内的可再生能源提升系统运行效益[5-7]。根据PIES配置约束的类型可将优化问题分为线性规划、混合整数线性规划、非线性规划等[8-11]。PIES 优化配置问题的优化目标根据实际需求可包括经济指标、环保指标（二氧化碳排放量）及节能指标（能耗、能源效率）等[12-14]。

前述研究主要集中在传统的电力系统运行场景下进行PIES 的优化配置分析，并没有考虑到PIES 与配电网进行能量交互和协调配合的内在需求。实际上，PIES 中稳定、高度自动化的工商业负荷具有较大的需求响应潜力。

文献[15]总结了需求响应建模的方法、调度架构及交易模式。文献[16]研究了电热负荷综合需求响应机制对提高PIES 热电联产经济性、灵活性和高效性的作用。文献[17]构建了冷热电需求耦合响应的PIES 优化运行模型及策略。文献[18-19]则从园区内部各运行主体的角度出发，利用强化学习、博弈论等理论工具进行需求响应策略研究。但文献[15-19]主要着眼于需求侧响应对电网运行的影响，未能在建设PIES 前考虑需求侧响应对优化系统配置的作用。

在上述研究基础上，以广州某园区为研究对象，兼顾PIES 的运行成本、污染排放和能耗3 个目标，考虑电力市场分时定价机制下的需求侧响应策略，建立PIES 多目标优化配置及多属性决策模型，分析需求侧响应对现阶段园区系统的影响，为PIES的建设和运行提供参考。

1 园区综合能源系统的基本架构

1.1 基本架构

图1 为一个典型的PIES 结构。园区内包含电、气、热、冷4 种能源类型及相应的终端负荷、能源转换设备和储能设备。

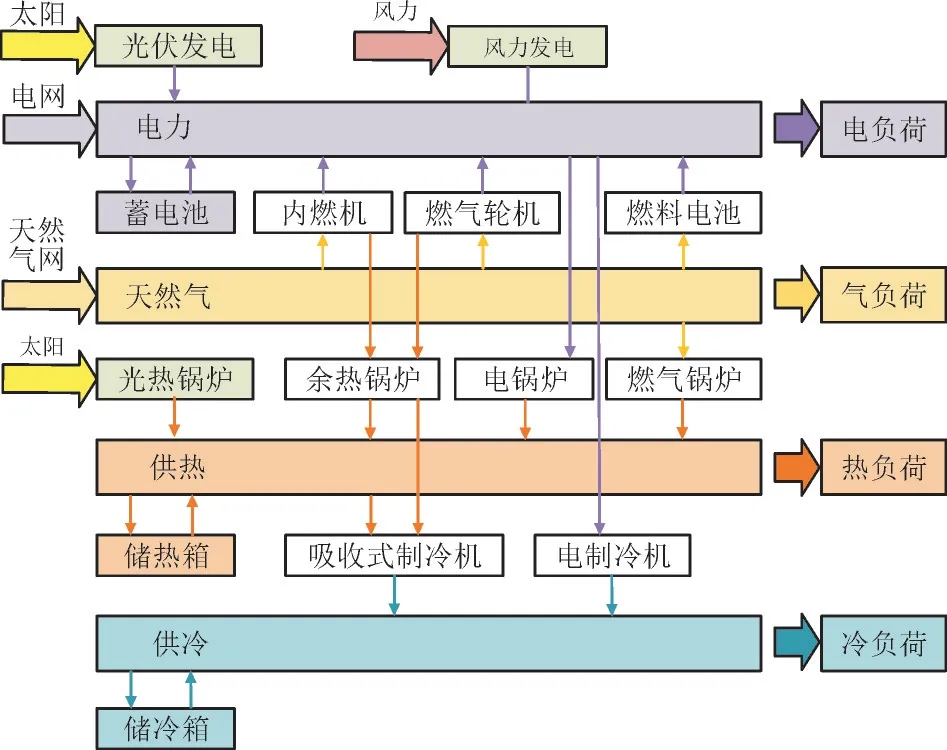
图1 典型PIES结构图Fig.1 Typical structure of PIES

1.2 设备特性及运行建模

1.2.1 设备的运行特性及状态约束

在变工况特性中，部分设备的工作效率会随着负载率的下降而急剧降低。为了简化规划设计阶段的分析过程，通常将设备的工作效率设定为常数。出于经济性考虑，为设备设定一个负载率边界值，当负载率低于边界值时关闭该设备。第i个设备的输出功率为：

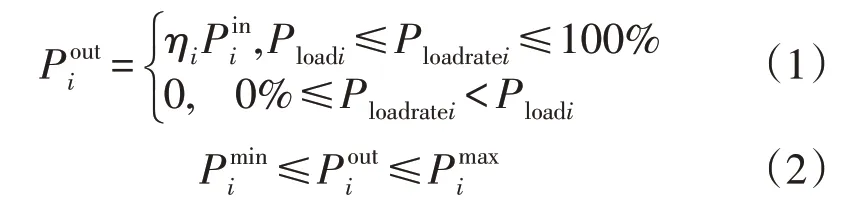
式中：为设备输入功率；ηi，Ploadratei和Ploadi分别为设备的效率、负载率和负载率边界值；和为设备输出功率的下限和上限。其中，Ploadi是效率边界值在设备变工况特性曲线上的交点。内燃机的变工况特性曲线在文献[20]中给出。

综合能源系统的日内运行计划一般以1 小时为计划间隔，计划内容包括设备的运行状态和输出功率。为每个设备分配二进制运行状态变量，设备的实际出力为：

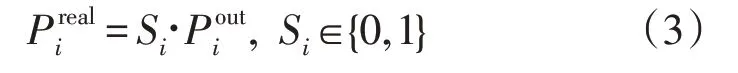
式中：Si为设备i的运行状态，取值0 为停机状态，1为正常运行状态。

1.2.2 储能设备约束

储能设备的运行状态可分为充能、放能和停运状态，为其单独增加充能和放能状态的运行约束：

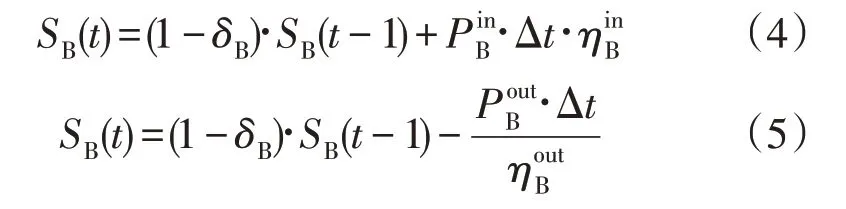
式中：SB为储能设备B 储存的能量；δB为储能消耗率；分别是输入和输出功率；分别是输入和输出效率；Δt是时间间隔。

储能设备可进行双向功率流动，但其充能和放能过程不能同时进行，为减少存储过程中的能量损失并降低存储容量成本，设定储能设备的充-放能周期，其约束为：

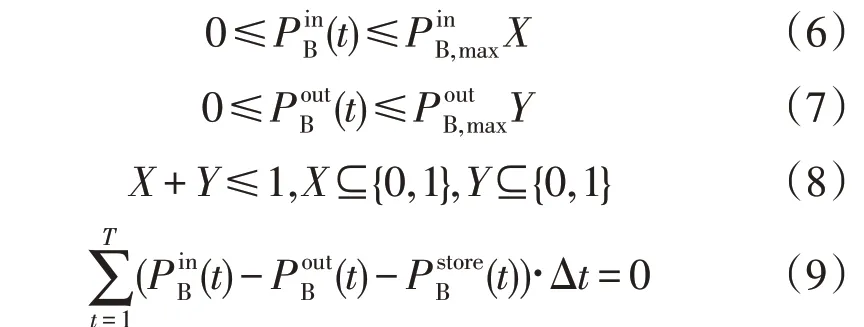
2 综合能源系统需求响应策略

需求侧响应的意义在于利用价格的变动影响用户现有的用能习惯，进而改善电网负荷特性曲线，降低电网的总体运行成本。园区用户按运营主体可分为传统用户和能源枢纽[21]。传统用户的大部分用能需求较为固定，剩余的用能需求是对价格敏感的价格型负荷，如部分电负荷；能源枢纽通过各种能源转换设备利用不同能源间的相互转化满足用户相同的用能需求，称为替代型负荷，文中所有负荷均属此类，由能源枢纽进行统一调度。

价格型需求响应是利用价格引导某一类能源需求转移到不同的时间点，而替代型需求响应则是不同类型的能源需求在相同时间点的相互替代[21-22]。两种类型的需求侧响应通过影响PIES 在各时段的各类能源消耗量来间接影响PIES 与配电网的电力交易量。

2.1 价格型需求响应

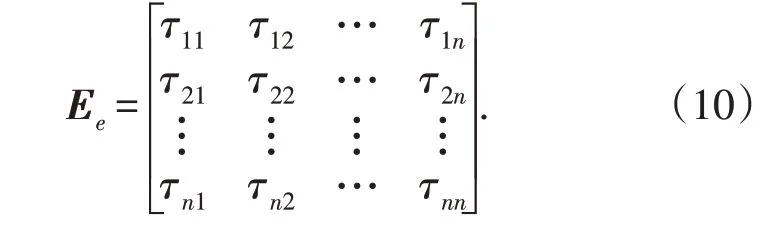
文中采用主流的电量电价弹性矩阵描述电力负荷需求响应，弹性系数是电量变化量与价格变化量的比值。弹性系数τab表示时段a的电量对时段b的电价变化的响应，其具体数值可通过对当地各行业的电量和电价统计数据进行多元回归计算得到。由各个时段间的弹性系数构成的电量电价弹性矩阵Ee如式（10）所示：

需求侧响应后n个时段的电负荷向量Qz为：

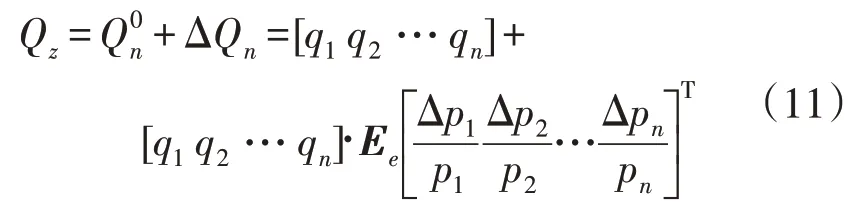
式中：为响应前的电负荷需求；ΔQn为响应后电负荷的变化值；Δq和Δp分别为电量q和电价p的变化量。

2.2 替代型需求响应

在PIES 中，电、气、热、冷等能源通过相关耦合设备（燃气轮机、各种锅炉和制冷机等）实现不同能源之间的转换，已具备能源枢纽的特征。能源枢纽可以对不同形式的能源进行转化，通过优化枢纽的运行方式来满足终端用户同等的用能需求，同时提高PIES 的经济性、灵活性以及能源的利用效率。各能源间的转换必须满足能量守恒定律，能源间的转换关系[22]为：

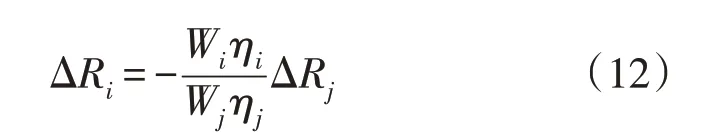
式中：i，j分别为两种不同的能源类型；ΔR为负荷增量；W为能源的单位热值；η为能源的利用率。

设响应后的替代型负荷为Li，为保证系统中各类型负荷总量不变，引入负荷平衡约束。即：

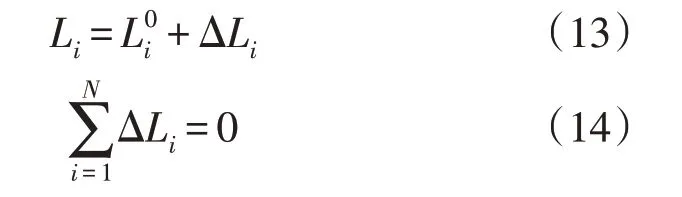
式中：为响应前的替代性负荷；ΔLi为需求响应的负荷变化量；N为能源耦合中的能源类型。

3 考虑需求侧响应的园区综合能源系统多目标优化配置模型

基于PIES 的基本架构，综合考虑园区各种负荷需求以及用户侧的综合需求响应，建立PIES 多目标优化配置模型，得到PIES 的最优配置及运行方案。

文中将所建立的模型分解为主问题与子问题，并进行迭代求解，如图2 所示。主问题以PIES 的总成本、污染排放量和能耗为优化目标，采用多目标群搜索算法（Multi-Objective Group Search Optimizer，MOGSO）优化PIES 的设备类型及容量，并将其作为已知参数传入子问题。子问题以PIES 的运行成本最小为目标，结合综合需求响应策略建立系统运行的混合整数线性规划模型，采用Gurobi 求解器求解模型，得到各类型设备的运行状态及最优小时出力，并将结果返回到主问题。最终，主问题根据子问题的优化结果计算当前设备配置下的PIES 的总成本、污染排放量和一次能源消耗量。MOGSO 经过多次迭代产生一系列帕累托最优解，这些最优解都是可行的系统配置方案。

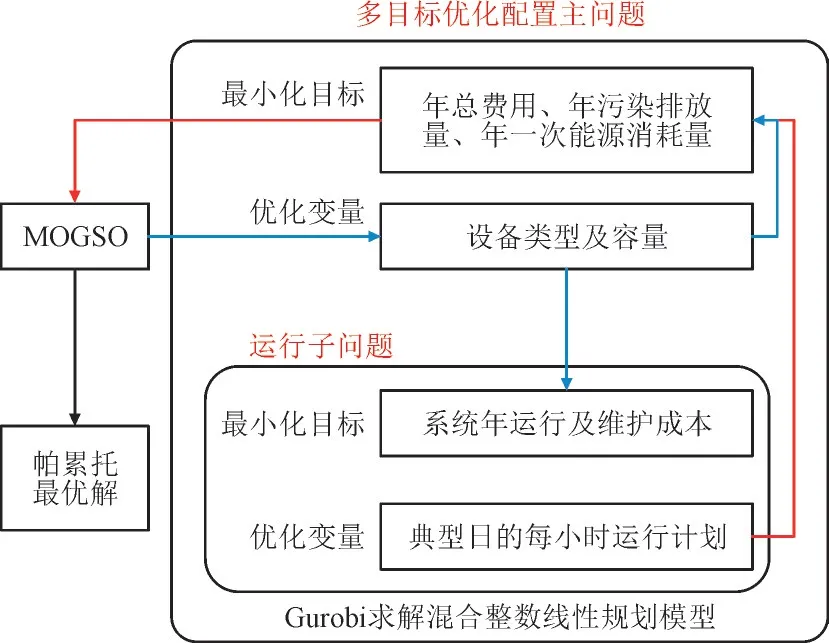
图2 多目标优化配置方法的流程图Fig.2 Process of multi-objective optimization configuration method

3.1 多目标优化配置主问题模型

文中考虑了规划周期年内的总费用、污染排放量和能耗量最小表征不同运行指标的目标函数。主问题的模型描述为：

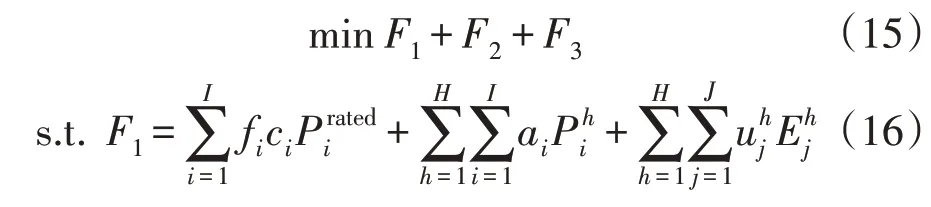
式中：F1为年总费用，为年等额投资成本、设备运行维护费用以及燃料费用的总和；I为设备总数；H为年运行小时数；J为输入能源类型总数。第一项是系统每一年的等额投资成本，fi和ci分别为设备的固定维护成本和单位投资成本为设备额定容量；第二项和第三项分别是设备运行维护费用和能源费用，ai为可变维护成本，为设备第h小时的有功输出和分别为第h小时能源j的价格和消耗量，PIES与配电网间的购电支出费用和售电所得费用已统一包含在能源费用中。即：

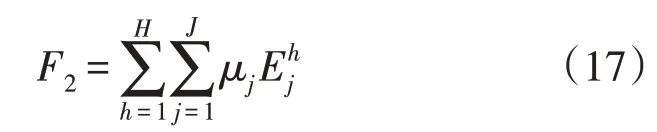
式中：年污染排放量F2采用等价CO2排放量计算，文中仅考虑电网燃煤发电、园区天然气发电以及园区天然气锅炉产生的污染排放；μj为能源排放系数。风能、太阳能等可再生能源的排放系数为0。即：

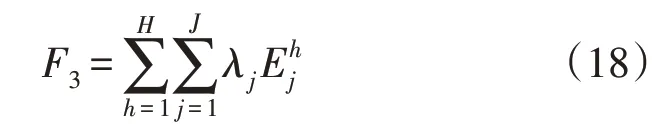
式中：年能耗量F3采用电网购电以及园区内消耗天然气的等价标准煤耗计算；λj为标准煤转化系数。

主问题的优化变量是系统中各类型设备的容量，包括固定容量的燃气轮机、内燃机的台数（离散变量）和其他设备的容量值（连续变量）。设备的容量选择受到园区资源、场地、技术等因素的限制，因此主问题包含设备数量及容量约束为：

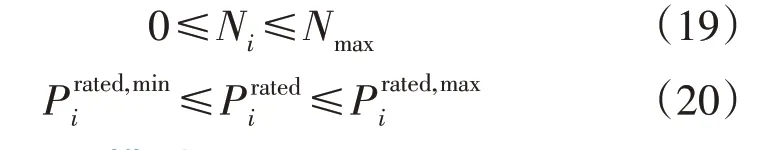
3.2 运行子问题模型

子问题的目标是使PIES 年F′总成本最小，包括运行成本、维护成本以及能源成本，针对每个季节选取1 个典型负荷日得到当年的负荷情况。子问题的模型为：

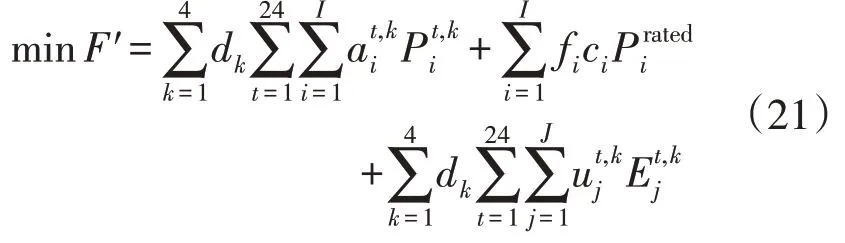
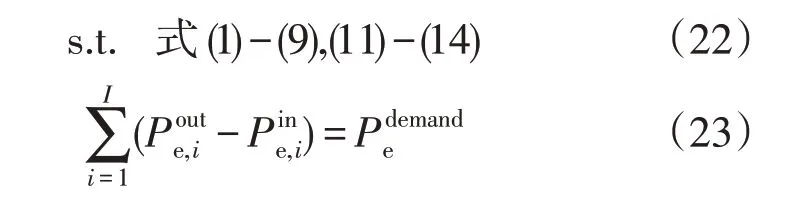
式中：dk为第k个典型负荷日在全年中的天数，每个典型负荷日有24 个小时；e 为能源类型，包括电、热和冷能；分别为设备的输入、输出功率和用户的负荷需求。

式（1）—式（9）为PIES 运行模型，式（11）—式（14）为需求侧响应约束，式（23）为每一时刻下PIES中各类能源的能量平衡约束。

子问题的优化变量包括各种设备的运行状态、输出功率和实际输出功率。

4 求解方法

本节给出图2 中的多目标优化配置主问题和运行子问题的求解方法，另外，PIES 的规划建设往往涉及多个利益主体，采用多属性决策方法从帕累托最优解中选出最能均衡各方利益的配置方案。

4.1 主问题求解方法——多目标群搜索算法

MOGSO 具有自适应搜索策略、允许混合类型变量、收敛速度快等优点，在多目标优化问题中已得到广泛应用。文献[23]将MOGSO 与粒子群算法（Particle Swarm Optimization，PSO）和传统的原对偶内点法（Primal-Dual Interior Point，PDIP）进行了性能测试与对比，结果显示MOGSO 在最优、最劣及平均最优解指标上都具有更高的精度，因此文中采用MOGSO 作为主问题的优化算法。

MOGSO 中主要有领头者、跟随者和游荡者3种角色，三者之间可以相互转换。领头者在全局范围内寻找最优值的可能区域，跟随者在此可能区域内进行详细的局部搜索，游荡者采用Lévy 飞行搜索策略避免整个种群陷入局部最优，保障全局收敛性[24]。

4.2 子问题求解方法

原规划问题的模型中，运行子问题式（3）是非线性约束条件，为便于运行子问题的求解，将式（3）转化为线性约束来提高优化速度：

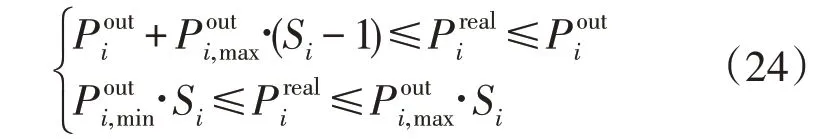
当Si=0 时，设备关闭，=0；当Si=1 时，设备开启，。式（24）中的线性化方法将原来的非线性约束转化为混合整数线性约束。

经过式（24）的线性化方法，运行子问题的模型转化为混合整数线性规划问题，该运行子问题的混合整数规划可直接调用现有的商业运筹优化求解器（如Gurobi、CPLEX）进行高效求解。

4.3 基于证据推理的多属性决策方法

决策者由于无法获取完整信息或者知识储备不足以做出判断时会产生不确定性评估，文中采用基于证据推理（Evidential Reasoning，ER）的多属性决策方法[25]在待选的帕累托前沿解中选出最符合实际需求的系统配置方案。该多属性决策方法的流程如图3 所示。

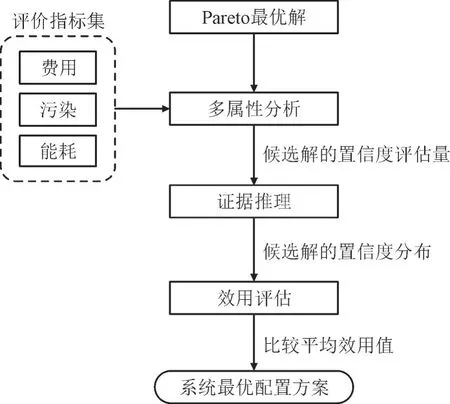
图3 基于证据推理的多属性决策方法流程图Fig.3 Process of multi-attribute decision-making method based on ER

5 算例分析

5.1 系统及设备参数

以广州某园区的规划设计为依据，应用所提出的PIES 优化配置模型及优化决策方法。经调查，该工业园区主要以电、热和冷负荷为主，满足使用太阳能的场地条件的面积为80 000 m2，可接入区域天然气网和区域电网，园区内可建设的设备种类及经济技术参数详见文献[26]。

需求响应的时间尺度与系统运行计划相匹配，均设为1 h。能源的峰谷平价格见表1，电量电价需求侧弹性系数[27]见表2。PIES 向电网售电的上网电价为当前时刻向电网购电电价的0.7 倍。

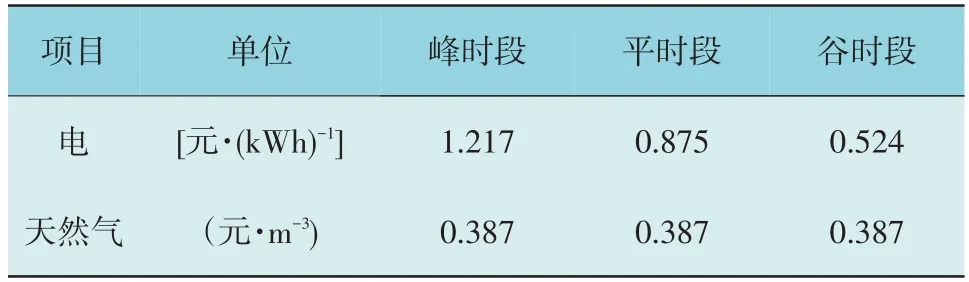
表1 能源的峰谷平各时段价格Table 1 Peak-flat-valley time-of-use energy price

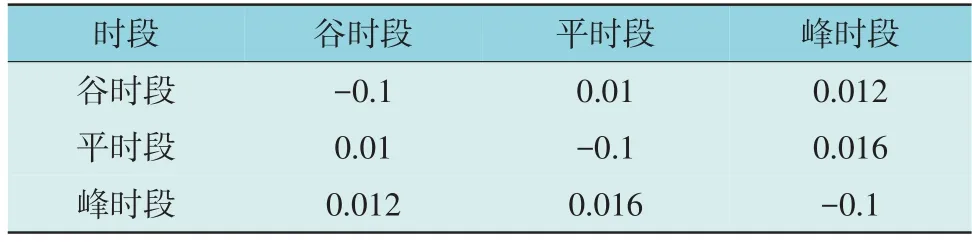
表2 电量电价弹性系数Table 2 Electricity price elasticity

该园区4 个典型日的电冷热负荷曲线、价格型需求响应后的电负荷曲线及太阳辐射密度曲线如图4 所示。

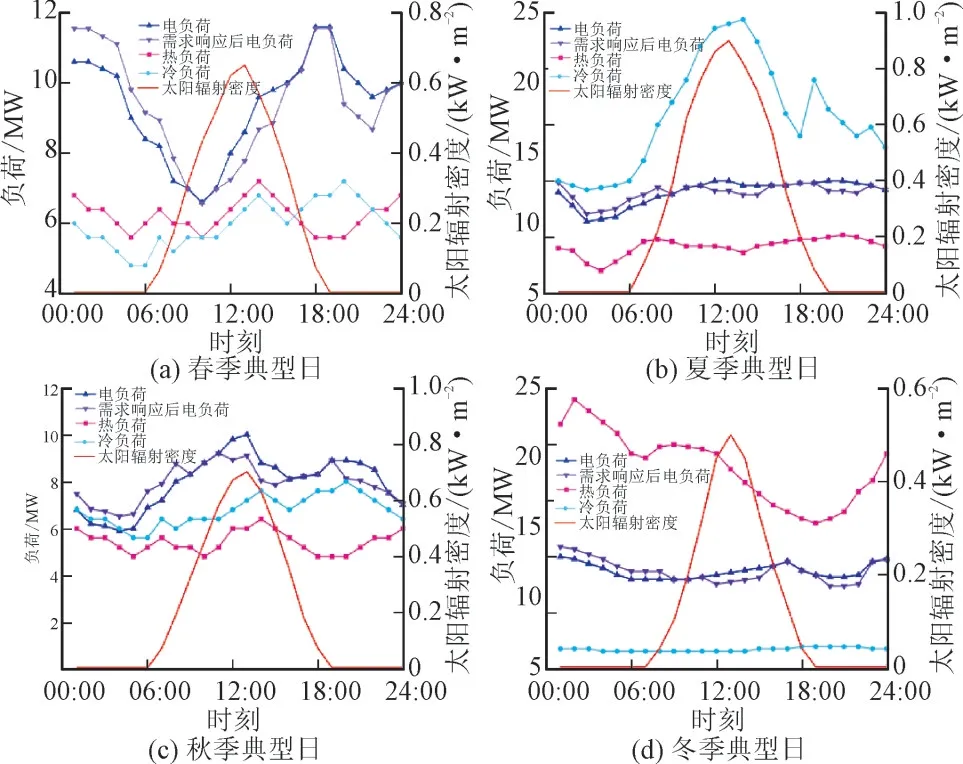
图4 该园区4个典型日的负荷及太阳辐射密度曲线Fig.4 Load curves and solar radiation density curves for park on four typical days

表3 列出了不同能源的CO2排放系数及标准煤耗转化系数。MOGSO 的迭代次数和种群数目均设为100。

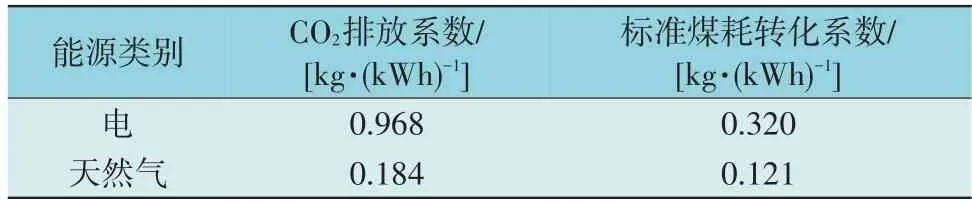
表3 能源的CO2排放系数及标准煤耗转化系数Table 3 CO2 mission factors for different energy and conversion coefficient of standard coal consumption

为了增强PIES 的稳定运行能力，考虑极端场景对系统的影响。结合综合能源系统的运行经验，在运行优化子问题中考虑以下极端场景：（1）可再生能源出力最大，持续时间4 小时；（2）系统各类负荷总和最大，且可再生能源出力很小。两种极端场景的设置如表4 所示。

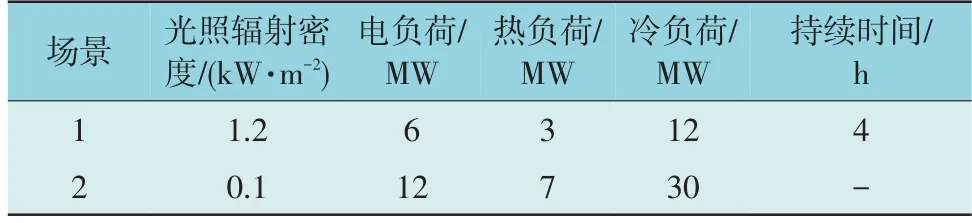
表4 极端场景设置Table 4 Extreme scenario setting

5.2 园区优化配置流程、结果及分析

在式（15）—式（20）的多目标优化问题中，定义了年总费用、年CO2排放量和年能耗量3 个评价指标来定量描述PIES 的综合效益。但在实际规划设计中，投资者对经济性指标的重视程度最高，污染排放指标次之，而且在相同的系统负荷下不同设计方案的能耗差别很小。因此，文中最终选择年总费用和年CO2排放量作为多目标主问题的优化目标，将能耗作为决策阶段的属性参与到优化中，将三维帕累托最优前沿压缩为二维，更高效地选择最优规划方案。

将PIES 设置为暂不考虑需求侧响应，通过MOGSO 优化得到下凸的帕累托前沿，前沿上的多个PIES 容量配置方案的总费用与污染排放存在相互矛盾的关系，年总费用较低的系统配置方案具有较高的污染排放量，年总费用较高时则具有较低的污染排放量。

为了进一步分析3 个优化目标之间的制约关系以及能源市场的交易情况，从图5 的帕累托可行解中分散地选出8 个可行方案，表5 给出了它们的3 个目标值以及与区域配电网、区域天然气网的交易量。由表5 可见，8 个方案的年总费用和年污染排放量呈负相关关系，而年能耗量只在小范围波动，进一步验证了减少规划目标的有效性。

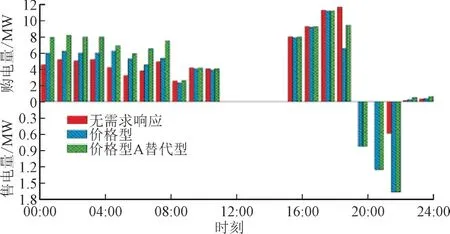
图5 春季典型日不同场景下的园区系统购售电量Fig.5 Purchasing and selling electricity of park-level PIES under different DR scenarios on a typical day in spring

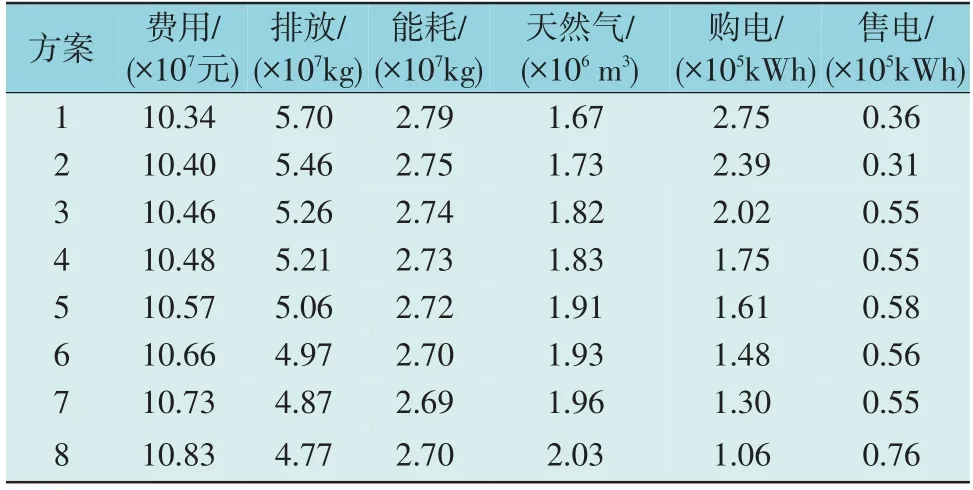
表5 多目标优化得到的8个方案的目标值Table 5 Objective value of eight schemes obtained by multi-objective optimization

为了综合考虑PIES 配置方案的经济性、环保性和节能性，利用多属性决策方法从8 个待选方案中选出系统最优配置方案。

一般来说，经济性指标是系统规划与设计中最重要的指标，应赋予总费用较大的权重系数，文中给3 个目标分配的权重系数依次为0.5、0.3、0.2。经过多属性决策得到各方案的评估结果，选择平均效用值最大的方案4 作为该PIES 的最优配置方案。

5.3 需求侧响应对园区优化配置的影响

如图4 所示，考虑价格型需求响应后，部分峰时段的电负荷转移到了谷时段，降低了区域电网的电负荷峰谷差的同时也降低了园区的用电成本。设置如下3 个场景进一步探究需求侧响应对园区综合能源系统优化配置的影响：（1）不考虑需求响应；（2）仅引入价格型需求响应；（3）引入价格型和替代型需求响应。

采用文中提出的方法分别得到对应场景下的系统最优配置方案的各个目标值如表6 所示，详细的系统配置方案在表7 中列出。图5 展示了电负荷波动最大的春季典型日在不同需求侧响应下的PIES 对电网的购售电量。

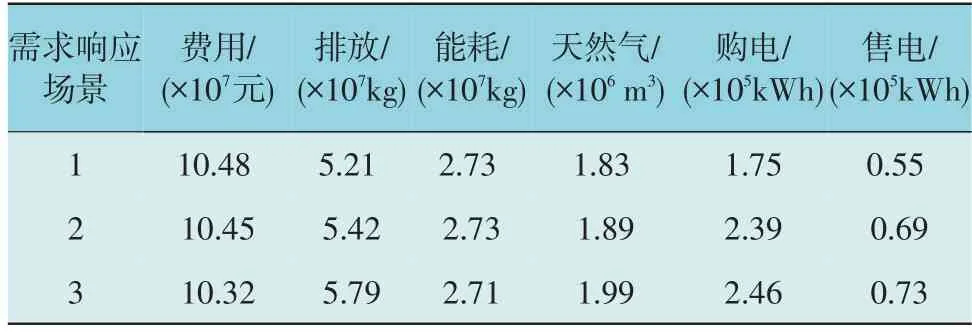
表6 不同场景下的园区最优规划方案目标值Table 6 Objective value of optimal planning scheme for park under different DR scenarios

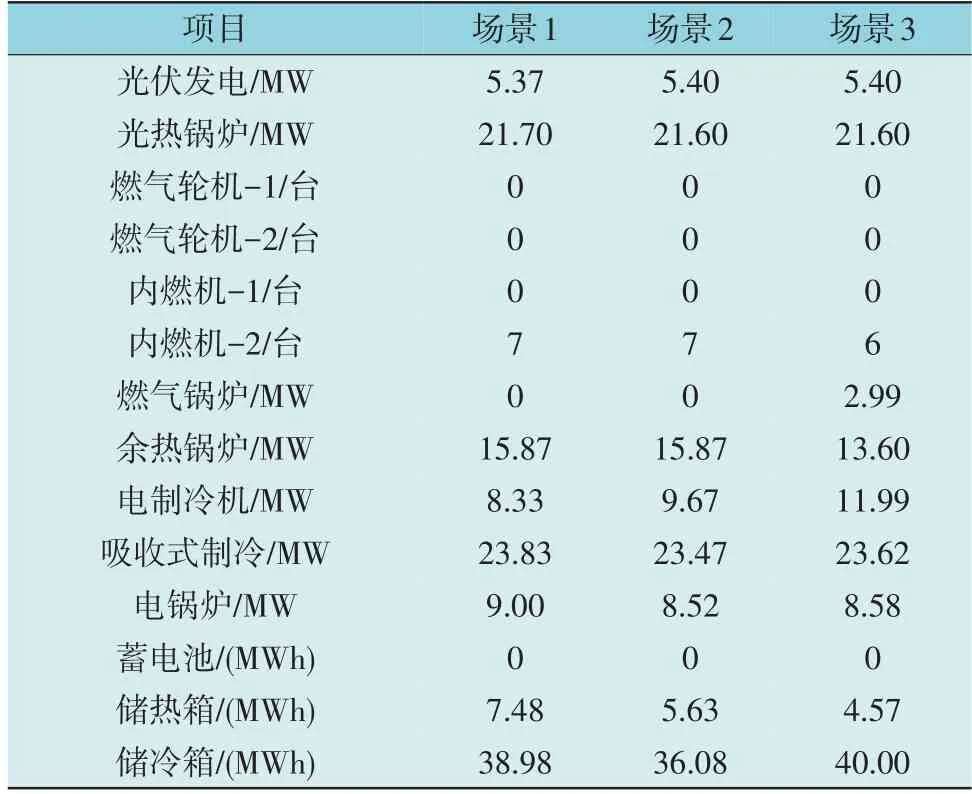
表7 不同场景下的最优园区系统配置方案Table 7 Optimal configuration of park-level PIES under different DR scenarios

结合表6、表7 和图5 以及优化过程数据分析如下：

1）在优化目标方面，考虑了需求侧响应后的PIES 具有更高的经济性，能耗量基本不变，但污染排放量急剧增加。相对于无需求响应的场景，对电负荷实行价格型需求响应后系统费用减少0.29%、污染排放增加4.03%；而加入了电负荷价格型和全部负荷替代型需求响应后系统费用减少1.53%、污染排放增加11.13%。对园区综合能源系统来说，考虑需求侧响应所节省的费用与要付出的环保代价并不匹配。

2）在设备选择方面，光伏资源在发电和制热之间的分配比例已达到均衡。由于内燃机-2 的电热效率比和成本在该园区中具有较大优势，因此系统仅选择内燃机-2 作为主力发电设备。余热锅炉容量与内燃机的数目呈正相关。由于蓄电池的成本过高，因此不考虑建设蓄电池。

3）加入电负荷价格型需求响应后，为降低用能成本，园区系统在谷时段增加电网购电来满足能源需求。但由于电网购电的污染排放系数大幅高于天然气发电，因此需求侧响应加重了园区用能的污染排放。此外，在园区负荷率较低的区域电网负荷峰时段（20:00-22:00），园区系统可以增加内燃机发电量并向电网售电，以覆盖部分的设备运行维护成本。

4）加入替代型需求响应后，园区系统通过能源耦合进一步提高设备的利用率，减少内燃机数目并增加燃气锅炉的建设，以填补余热锅炉和储热箱的热源缺口。在电网电价的谷时段购入更多廉价电能，增加电制冷机和储冷箱容量以满足冷负荷需求，进一步降低园区运行的年总费用。

5）12:00-15:00 属于电网用电峰时段，电网购电成本较高，此时园区光伏出力处于最大时段，可以满足一部分电负荷及冷热负荷需求，剩余负荷缺口通过内燃机发电来弥补，达到最经济的运行方式。

6 结语

提出了一个考虑需求侧响应的园区综合能源系统多目标优化配置计算及决策方法，该方法以最小化系统总费用、污染排放和能耗量为优化目标，将配网电力交易额包含在能源费用中，通过需求侧响应间接影响园区综合能源系统与配电网的电能交互。结合用户需求和各类设备的约束条件建立优化配置模型，利用多目标群搜索算法求解可行方案，最后采用基于证据推理的多属性决策方法选择最优的系统配置。算例结果显示，帕累托可行解包含了一系列的可行配置方案，对待选方案进行多属性决策的平均效用值评估后能得到最优的园区综合能源系统配置方案。另外，用户及园区综合能源系统的需求侧响应可以进一步降低系统规划和运行费用，但会造成园区用能污染排放量剧增。