立式装盒机开盒问题分析与解决方法

刘显龙

（广东机电职业技术学院，广东 广州 510000）

0 引言

装盒机是一种重要的包装机械，根据工作时盒子的状态可将其分为立式装盒机和卧式装盒机。装盒速度是衡量装盒机性能的重要指标，以装盒速度划分，装盒机分为中低速、中高速和高速三类，国外装盒机最高运行速度已达12000 盒/min，中国大部分装盒机仍位于中低档，与国外同类产品差距较大[1，2]。

国内外许多学者从吸盘末端运行轨迹、运动特性着手，对装盒机关键部件及机构参数进行优化，不断提出新的取盒方案，以实现装盒机高速化目的。SIRKETT 等[3]提出了行星轮系取盒机构，对影响吸盒成功率的因素进行了研究，研究发现纸盒的材料和机构转速对吸盒后放盒成功率有影响。李龙等[4]提出了一种基于内摆线轨迹的高速取合机构。童俊华等[5]提出了椭圆-行星轮系驱动的取盒机构，并研究了椭圆-行星轮系的参数对内摆线轨迹及运动特性的影响。

在开盒过程运动和力学分析基础上，探讨了开盒成功率的主要影响因素，并进一步提出了解决思路。

1 挤压式开盒过程及存在问题

立式装盒机应用杠杆原理，通过挡、压的方式实现开盒，过程：吸盘吸住纸盒向右运动，在（b）位置与挡柱4 发生碰撞，在力F 的作用下完成初步开盒，然后继续向右运动，在模板口的导向作用下完全打开，如图1 所示。

图1 挤压式开盒过程

生产过程中，当存在纸盒质量材质硬，拆弯处压痕浅，内部有粘连，纸盒面与面间贴合紧，或者纸盒材质软，且各面贴盒紧或各面间残留有胶水等情况时，开盒失败概率突增。

2 开盒动作的运动及受力分析

为便于分析开盒成功率的影响因素，将纸盒简化为四连杆机构（图2），并作如下约定：杆长BC＝2AB＝2CD＝2l，质量MBC＝2MAB＝2MCD＝2 m，连杆1 与圆柱的接触点距离铰链A为l1，忽略圆柱与连杆间的滑动摩擦力以及各连杆所受重力，开盒过程中纸盒所受的转动阻力为M，它不随连杆机构的运动产生变化，并集中施加在杆1 上。

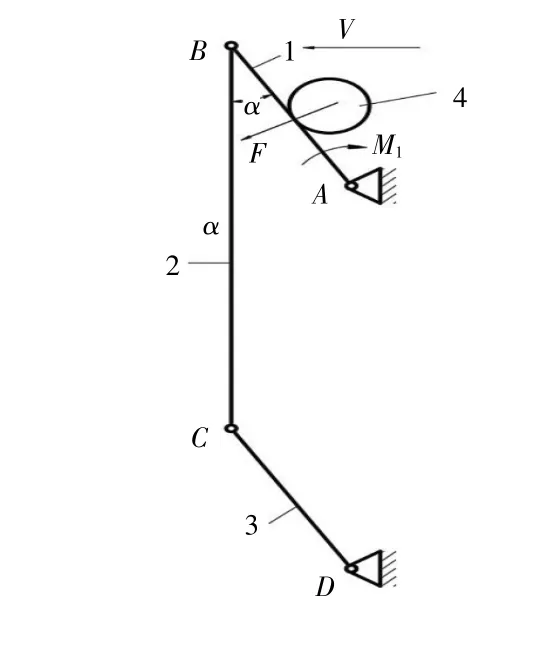
图2 纸盒简化四连杆机构

2.1 碰撞过程纸盒运动和受力分析

以杆1 和圆柱4 碰撞时间为界，将开盒过程可分为碰撞和非碰撞过程。纸盒与圆柱4 碰撞前，它们以速度v作相对运动，α角等于零，四连杆相对铰链A和D静止。当圆柱4 与杆1 碰撞时，在力F的作用下，杆1 和杆3 分别绕铰链A、D作角加速度运动，杆2 作平动。因为此机构是平行四连杆，因此，杆3 和杆1 具有相同的角加速度和角速度。根据碰撞的相关理论，可知：

其中，l1是圆柱4 与杆1 接触点到铰链A的圆心距离，J是杆1、3 的转动惯量，ωA0是碰撞前杆1 绕铰链A的角速度，ωA1是碰撞后杆1 绕铰链A的角速度。

式（1）中，等号左边是作用在杆1 上的冲量矩，它是力F与纸盒转动阻力的合力矩M在碰撞时间内的积累，右边是碰撞前后的动量矩变化量。因为力F除了让杆1 产生动量外，也通过杆2 的连接作用让杆3产生相同的动量，因此，对式（1）进行修正，得：

因为杆1、3 在碰撞前相对铰链A 静止，因此ωA0＝0，式（2）简化为：

根据碰撞相关理论，碰撞时间t通常只有零点几秒，在这么短的时间内，杆1 碰撞前后转动的角度非常小，为便于分析，忽略杆1 在碰撞过程中发生的转动，即，在碰撞结束瞬间，α≈0，因此，杆1 的角速度是：

代入式（3）得：

由式（5）可知，碰撞时，杆1 受到的力F与杆1、2的转动惯量J，碰撞时间t、碰撞前纸盒运动速度v、碰撞接触点至铰链A的距离l1及纸盒面转动时所受阻力M有关。

2.2 非碰撞过程纸盒运动和受力分析

碰撞完成后，杆1、3 在力F和扭矩M的共同作用下继续绕铰链A 和D 转动，杆1 和圆柱4 的接触点的速度ν不变，将它沿杆1 轴线及垂直轴线方向进行分解（图3）。

图3 纸盒非碰撞过程

杆1、3 的角速度为：

其中：ωA2是非碰撞过程杆1、3 的角速度。由式7 知，在0～ π 角度范围内，随着角度α增大，cosα值减小，同时，l1值随着增大，在值减小且l1值增大情况下，ωA2值减小。因此，碰撞结束瞬间，杆1、3 的角速度达到最大值ωA1，即ωA2＝ωA1，然后减小。算式（2）依然适用于非碰撞过程，得：

其中，t1是碰撞后力F作用时间。由式（8）知，因为JωA2>JωA1，等式右边小于等0，因此，Fl1-M≤0 ⇒，又因为开盒过程中l1值一直增大，因此，F值在非碰撞过程中一直减小。

由上述分析可得知：纸盒在开盒初始阶段受到非常大的碰撞冲击作用，所受力在极短时间内由0 增大到最大值F，然后逐渐减小。

3 开盒失败原因分析

生产过程中，吸盘主要承受的负载是纸盒重量及圆柱施加的力F，由于纸盒较轻，因此吸盘的主要负载是力F。开盒过程中存在影响F稳定的因素，它们使负载超出吸盘吸引力，导致纸盒脱落。讨论力F的影响因素，以进一步分析开盒过程存在的问题。

（1）运动速度v对力F的影响

根据上述分析可知，纸盒碰撞瞬间力F达到最大值，然后逐渐减小。由式（5）可知，碰撞过程中，速度v与力F是一次线性函数关系，其斜率，常数b＝M/l1。生产中，生产速度提高时，纸盒运动速度加快，碰撞瞬间纸盒承受的冲击力F就越大，越可能超出吸盘的承受能力并导致纸盒脱落。

（2）恒定扭矩M对合力F的影响

纸盒各面间存在转动阻力，它与纸盒生产质量相关，比如纸盒压痕越深，阻力越小，反之，阻力越大；纸盒内残留的胶水越多、纸盒各面间贴合越紧阻力也越大。在上述分析过程中，把这些阻力简化为扭矩M。由式（5）知，力F与阻力M也是一次函数关系，其斜率k＝1/l1，常数b＝，力F随M值增大而增大。如果吸盘吸力值设置太小，阻力M值的变大有可能使力F超过吸盘能承受的最大负载，导致开盒失败。

（3）纸盒材料软硬对力F的影响

不同纸盒材料有软硬区别，根据碰撞相关理论，在碰撞过程中，越软的纸盒，碰撞时间t越大，越硬的纸盒，碰撞时间t越小。由式5 知，t值减小时，F与V函数的斜率K 增大，相同运行速度碰撞后的力F也增大，可能会超出吸盘承受负载的极限，导致纸盒脱落，开盒失败。

另外，对于较软的纸盒，碰撞时，纸盒在强大的冲击力下会产生弯曲变形，不能按四连杆机构运动方式正常打开。

4 结语

由前面的分析可知，挤压方式开盒通过碰撞使纸盒获得开盒动力，由于碰撞产生的力非常大，且不可控，同时，生产速度和纸盒硬度等不确定因素会引起碰撞力F较大变化，这些问题限制了生产的速度和效率，因此，挤压式开盒方式是提升装盒设备效率的主要瓶颈。

为了避免上述问题，提升设备生产效率和稳定性，试提出以下解决思路：

如图4 所示，纸盒在（a）位置时，吸盘将纸盒吸出，当纸盒移动到（b）位置时，另一吸盘吸住纸盒另一侧，在纸盒向右运动过程中，两吸盘产生相对运动将纸盒拉开，然后纸盒继续向右运动，将纸盒送入模板口。相对于挤压式，这种方式通过两吸盘相对运动实现开盒，让纸盒避免了开盒过程所受的巨大冲击力，极大降低了纸盒变形及脱落的概率，能有效提高取盒的效率，增加生产稳定性。

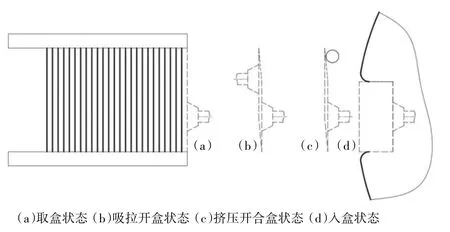
图4 吸拉式开盒