小圆心角小圆弧半径精确测量方案研究

陆雨薇，秦世林，蹇松阳，刘江东，尹利钊

（1.广西科技大学 广西土方机械协同创新中心，广西 柳州 545006；2.上汽通用五菱股份有限公司 广西新能源汽车实验室，广西 柳州 545007）

0 引言

随着汽车走进千家万户，消费者对汽车造型细节上提出了更高要求。近年来，汽车覆盖件间隙面差细节逐渐成为表达汽车造型美观的重要评价指标[1]，如大众CC、奥迪A3、小鹏P7 等，上述几款车型均以汽车覆盖件间隙美观优势赢得了良好的口碑和不菲销量。间隙面差广泛存在于汽车“四门两盖”间，其轮廓尺寸一致性严重影响人们对汽车外观精致美观的评价[2]。

传统汽车间隙面差测量是人工塞尺测量，测量精度低，稳定性差，其精度严重影响车身覆盖件冲压装配工艺水平，致使出现车身覆盖件间间隙分布不均匀、“老鼠洞”、风噪等现象[3]，严重影响汽车表观质量，以及驾驶安全性以及乘坐舒适性，最终影响消费者对汽车的购买欲望[4]。使用机器视觉测量是完美的替代方案，可有效改善上述问题，但需要先准确找到间隙两端小圆心角小圆弧上的特征点位置信息才能进行间隙面差的测量。

由于汽车“四门两盖”间隙中小圆弧的半径一般为1～ 2 mm，轮廓所对应的圆心角小于60°，经机器视觉相机采集到的圆弧部分数据较少。在通常情况下，圆弧半径越小，可用信息点越少，圆弧测量难度越大，拟合误差值越大，准确度越低[5]。对于圆心角较小的同一组数据，采用不同的拟合方法得到的结果可能会相差较大，甚至采用相同的方法去测量，得到的重复性精度也难以得到保证，无法判断哪个结果是准确可靠的[6]。

目前，针对小圆心角小圆弧的测量，相关研究较少。罗智孙等[7]提出一种基于三次指数平滑的方法，根据小圆弧点云轮廓趋势分别向圆弧轮廓两端预测部分点云扩大点云圆弧轮廓所对圆心角，以增多可用信息点数目，理论上提高了圆弧测量的精度，但是其在保证测量精度的情况下仅能增大5°圆心角，增加可用信息点数目效果甚微，并且预测点相对于真实点来说误差较大；Guevara 等[8]提出一种基于平均绝对误差的鲁棒几何拟合方法，该方法利用一种基于左右偏导数的算法替换传统算法改善传统算法目标函数不可微的问题，结合基于梯度或二阶导数的快速迭代算法，进行非线性规划识别并去除零件圆弧轮廓上的异常值，进而提高测量精度；朱嘉等[9]提出一种基于圆心约束的最小二乘法，根据模夹具定位圆心坐标位置，再约束圆心位置拟合得到圆弧半径，理论上提高了小圆弧的测量精度，但该方法已知圆心位置不适用于汽车生产制造过程中的小圆心角小圆弧的测量。同样，还有极少数使用较为昂贵的高精度相机进行检测，但相机全靠进口，价格昂贵且技术封锁严重，不可广泛推广，仅适用于小批量检测。

因此，在工程应用上需要一款成本低、效率高、精度高、可广泛推广的，拥有自主知识产权的测量小圆心角小圆弧的设备。本研究以此为切入点，使用低成本线结构光相机进行算法二次开发，通过增加圆弧轮廓可用信息点数量开展研究。

1 小圆心角小圆弧精确测量方案设计

由于汽车“四门两盖”间隙中小圆弧的半径较小（通常为1 mm～ 2 mm），圆弧轮廓较少，且车身钣金件冲压精度不高，难以通过实物实测（由于零件较小，间隙缝太小，高精度三坐标机测头无法进入缝隙测量）的方式开展实验验证[10]。对此采用加工精度为0.05 mm 的圆弧类标准件（图1）模拟“四门两盖”间隙中小圆弧，取其中理论半径分别为1 mm，2 mm，5 mm的圆弧进行点云数据采集并控制圆弧所对圆心角为30°、45°、60°、90°，进而验证本研究提出的测量方案的有效性，其中5 mm 组、90°组为对照组。

图1 标准件实物

首先，数据采集并提取圆弧轮廓，通过限制拍摄角度范围，变换线结构光相机拍摄位姿对标准件圆弧处进行多次拍摄，尽可能采集圆弧轮廓数据，提取出圆弧轮廓数据；然后，进行点云粗配准，通过将多组不同角度拍摄提取得到的小圆心角小圆弧点云进行配准，增加小圆心角小圆弧的点云密度以增多其可用信息点数量；再结合本研究提出的拉普拉斯深度平滑，将点云进行平滑处理，得到较光滑的圆弧轮廓点云；最后，利用最小二乘法进行拟合得到小圆心角小圆弧的半径。

1.1 数据采集并提取圆弧轮廓

通过限制拍摄角度范围，使用线结构光相机变换位姿多次拍摄标准件圆弧位置，如图2 所示。此时拍摄角度应控制在±20°左右，以此来得到更加优质的点云数据。此时的点云轮廓曲线为一段直线与一段圆弧的结合体，然后进行圆弧轮廓提取。由于直线与圆弧部分曲率相差较大，所以可以通过曲率筛选来提取圆弧。本研究通过Zhang 等[11]提出的3 点拟合曲线再求解曲率，设置阈值剔除直线部分点云，最终得到圆弧轮廓。

图2 数据采集

通过变换相机位姿拍摄，最终提取得到的相对于整个轮廓ab位置的圆弧轮廓曲线cd、ef，详见图3 所示。

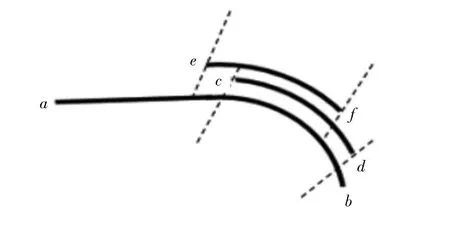
图3 圆弧轮廓提取

1.2 小圆心角小圆弧点云轮廓粗配准算法选择

点云配准，即通过求解不同坐标系下点云之间的平移矩阵T与旋转矩阵R，将源点云{Ps}变换到目标点云{Qt}坐标系下。常用的点云配准方法有ICP 算法（找到源点云与目标点云中距离最近的点对，根据估计的变换关系来计算距离最近点对经过变换之后的误差，通过不断的迭代直至误差小于某一阈值或者达到迭代次数来确定最终的变换关系，进而使两点云轮廓大体位置对齐）、PFH 算法（通过使用多维直方图来泛化点周围的平均曲率进而编码点的k 邻域几何特征，进而依据几何特征进行配准）、4PCS 点云配准算法（根据刚性变换后交点所占线段比例不变以及点之间的欧几里得距离不变的特性，在目标点云中尽可能寻找全等四点集，并利用最小二乘法计算得到变换矩阵，根据最大公共点集得到最优变换，进而完成配准）等[12]。

由于点云有波动，从间隙两端轮廓点云中提取出的小圆弧不一定是从圆弧与直线相切点开始的，并且每段小圆弧可用信息较少，导致小圆弧的配准没有具体特征点。所以，对于小圆心角小圆弧的配准仅需进行粗配准，将每段小圆弧大体位置对齐即可，正好适用于ICP 算法，其精度高，不需要提取特征点[13]。方法原理如下：

首先，对源点云{Ps}中的每一点pi（i∊1，2，…，N），利用kd 树最近邻查找算法寻找其在目标点云中的最近点qi（i∊1，2，…，N），组成一一对应的点对，再计算两组点云的质心，分别记为up，uq，其计算式为：

然后，对两组点云进行去质心，得到：

接着，构建矩阵H，并对矩阵进行SVD分解，即可求得旋转矩阵R与平移矩阵T。

在得到旋转矩阵R，与平移矩阵T后，将待配准的点云转换到新的点集{Uf}，设置源点云与目标点云欧氏距离平方和阈值，并代入目标函数：

若新变换的点集{Uf}与目标点集{Qt}之间的欧氏距离平方和小于阈值，则停止迭代计算，否则新的变换点集{pi}继续迭代，直到满足阈值条件。最终，配准后的小圆心角小圆弧点云如图4 所示。

由图4 可知，配准前的小圆心角小圆弧点云有波动，较为稀疏，可用信息点较少，并且由于相机在采点时反射等原因致使部分点缺失；反观配准后的小圆心角小圆弧，点云虽有波动，但点云更加密集，可用信息点更多。

图4 小圆心角小圆弧点云配准前后

1.3 基于拉普拉斯深度平滑的算法设计

由于采集的数据常受到样本表面精度、光照、拍摄抖动等的影响，单组点云数据的波动不可避免。同样经过如1.2 节所示ICP 算法的处理，待测点云集的缺失和数据量虽然得到了补充，但经过配准后的数据集并未完全重合，且波动依然存在。波动的点云会大幅影响检测水平，于是点云平滑处理应运而生，通过平滑处理去除离群噪点，降低点云的波动程度，达到检测精度要求。

现如今最常用的平滑处理算法主要有移动最小二乘法平滑、基于结构特征的平滑、滤波平滑等三类[14]。移动最小二乘法平滑是一种通过建立拟合函数、确定权值来进行处理的算法，通常适用于结构简单，函数明确的曲线[15]；基于结构特征的平滑也称为均值平滑或拉普拉斯平滑，是最简单的一种平滑处理方法，通常认为某点局部领域中点是其理想位置，并将邻域点移动到中点的平均位置。因此，该方法可能会破坏点云的拓扑结构，所以此方法处理效果较差[16]。两步平滑，先将相似法线平均在一起，进行法线的平滑，再移动顶点位置到适合新法线的位置，同样可能会破坏模型的拓扑结构。经过本研究配准后的小圆心角小圆弧点云波动大，排列情况复杂，且点云信息缺失严重，所以不适用于上述方法。

针对上述算法缺点和上述数据集特点，将传统拉普拉斯平滑算法与两步平滑算法结合，提出一种拉普拉斯深度平滑算法，在点云模型中添加边缘约束，并使用权重优化点的重定位拉伸，改善了传统拉普拉斯平滑算法与两步平滑算法破坏模型拓扑结构的问题。算法流程如图5 所示，算法的步骤如下：

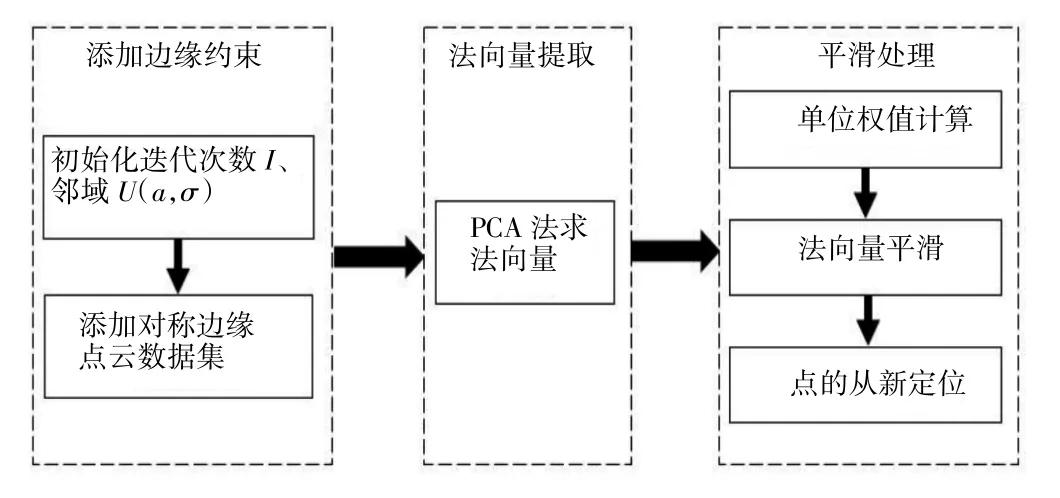
图5 拉普拉斯深度平滑算法流程

（1）U（a，σ）、Ω

（2）以a为对称中心，求Ωa～a+σ/2～a、的对称点集Ωf、Ωe，令Ω＝Ω∪Ωf∪Ωe

（3）法向量求取

（a）遍历∀Di∊Ω，得Ui

（b）求Ui的V、D，得ni

（4）平滑处理

其中Ω 为点云全集，a为起末点，σ为邻域范围，Ωf、Ωe分别为边缘添加点集，V、D分别为特征值与特征向量，Ωcf为单个邻域点集，Wcf为单个邻域内点的权值为法向量，di为点的移动距离，其中：U（a，σ）＝。

经过上述拉普拉斯深度平滑处理后，配准后的小圆心角小圆弧点云相对整个圆弧来看较为光滑。并且，由于在平滑时加入了单位权值，约束了各点的平滑方向以及点的重定位移动距离，即使在端点处的点云也不会受邻域点的影响，破坏原始点云的拓扑结构，平滑处理效果较好。经拉普拉斯深度平滑处理前后点云示意如图6 所示。

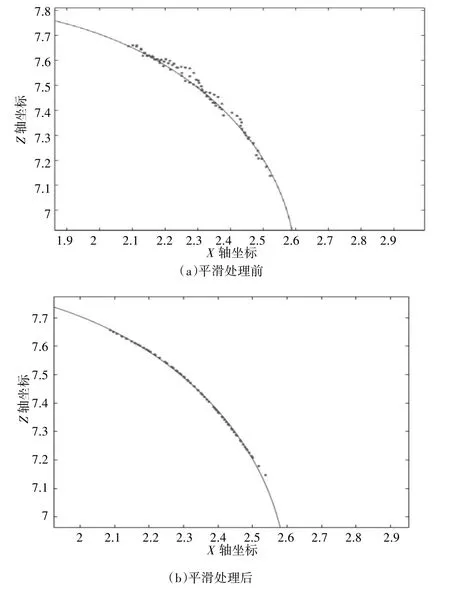
图6 拉普拉斯深度平滑处理前后点云

2 实验与分析

本研究通过小圆心角小圆弧半径拟合的平均相对误差来评价本方案算法的有效性，即用小圆心角小圆弧拟合半径ri与标准件圆弧半径r的误差值Δr相对于标准件圆弧半径r的比值绝对值的百分比的平均值。

其中，λ 表示小圆心角小圆弧半径拟合的平均相对误差，n表示拟合实验次数，r表示标准件圆弧半径，即基准值；ri表示第i次小圆心角小圆弧点云拟合半径，即实际值。

本研究采用控制实验流程变量进行对比实验分析，实验方案如表1 所示。分别取圆弧轮廓所对圆心角度数分别为30°、45°、60°、90°，标准件半径分别为1 mm，2 mm，5 mm 的圆弧数据分别进行10 次实验验证。其中各方案所对各圆心角的半径拟合平均相对误差如图7 所示。经本方案处理后各圆心角度数圆弧半径拟合相对误差如图8 所示。

图7 各方案平均误差分析

表1 控制实验流程变量对比实验方案表

对比方案2 与方案1 可知，当小圆弧所对圆心角度数为30°～ 60°时，未经任何处理的小圆心角小圆弧点云半径平均相对误差比经拉普拉斯深度平滑处理的小圆心角小圆弧半径拟合平均相对误差低13.3%。原因在于此时的小圆弧点云数量较少，拉普拉斯深度平滑在处理这类点云时会误把小圆弧点云认为直线点云，而进行过度的点的重定位拉伸，致使小圆弧拟合数据偏差较大。当小圆弧所对圆心角度数为60°～90°时，经拉普拉斯深度平滑处理的小圆心角小圆弧点云半径平均相对误差比未经任何处理的小圆心角小圆弧点云半径拟合平均相对误差低2.38%，原因在于小圆弧点云数量增加后，拉普拉斯深度平滑受到点的约束，从而对小圆弧点云进行适量的拉伸，降低了点云的波动，提高了半径拟合的精度。因此，仅使用拉普拉斯深度平滑提高圆弧点云半径拟合精度，在圆心角度数较大（大于60°）时，即可用信息点数量较多时，效果较好。

对比方案3 与方案1 可知，当小圆弧所对圆心角度数为30～ 60°时，经ICP 点云配准的方案3 中小圆心角小圆弧的半径拟合相对误差比未经任何处理的方案1 中小圆心角小圆弧的半径平均相对误差低5.63%。原因在于，ICP 点云配准增加了可用信息点数量，致使小圆弧点云半径拟合精度相对提高，但依然处于较高水平。当小圆弧所对圆心角度数为60°～90°时，由于未经任何处理的小圆弧点云相对较光滑，而经ICP 点云配准后的小圆弧波动更加明显，最终导致半径平均精度降低3.13%。因此，仅使用ICP 点云配准提高圆弧点云拟合精度适用于可用信息点较少时。

对比方案2 与方案4 可知，当小圆弧点云都经过拉普拉斯深度平滑处理后，加入ICP 点云配准步骤引入了更多的可用信息点，同时与拉普拉斯深度平滑共同作用提高了小圆弧拟合的精度，半径平均相对误差降低了25.37%。因此，ICP 点云配准步骤对本方案十分重要。

对比方案3 与方案4 可知，经ICP 点云配准后，圆弧上点云数量增多，但圆弧点云的波动增大，加入拉普拉斯深度平滑步骤降低了圆弧上点云的波动，可明显提高小圆心角小圆弧半径拟合精度，半径平均相对误差降低了13.24%。因此，拉普拉斯深度平滑步骤对本方案十分重要。

由图8 可知，经本方案处理前后各圆心角度数圆弧半径拟合相对误差提升较大，效果较好。其中，30°圆弧半径拟合平均相对误差降低了32.41%；45°圆弧半径拟合平均相对误差降低了22.35%；60°圆弧半径拟合平均相对误差降低了6.78%；90°圆弧半径拟合平均相对误差降低了0.72%。

图8 处理后各圆心角度数所对半径平均相对误差

综上所述，本设计的小圆心角小圆弧精确测量方案无论在圆心角度数较低时，或者圆心角度数相对较高时，均可提高圆弧半径拟合精度。其改善了小圆弧所对圆心角度数为30°～ 60°时，可用信息点数量不够引起的拉普拉斯深度平滑过度拉伸的问题；同时，也改善了当小圆弧所对圆心角度数大于60°时，点云配准带来的较大的点云波动的问题。综合应用上述步骤，小圆心角小圆弧的绝对精度可控制在0.06 mm，效果良好，满足了小圆心角小圆弧测量要求。

3 结语

针对汽车覆盖件中“四门两盖”的小圆心角小圆弧的精确测量提出了一套小圆心角小圆弧精测量方案，适用于圆心角度数为30°～ 60°的圆弧进行半径测量。通过多角度数据采集提取圆弧轮廓，利用ICP 配准算法将各角度拍摄提取的小圆心角小圆弧点云进行配准，提高点云密度，增加可用信息点数目，最后通过本研究提出的一种拉普拉斯深度平滑算法减少配准后点云的波动，并使用最小二乘法拟合圆弧。经实验对比发现，本研究所提出的小圆心角小圆弧精确测量方案有效提高了拟合精度，绝对精度可控制在0.06 mm，满足小圆心角小圆弧测量要求。

针对工程应用上，其工程实际应用价值较高，实用性较强，通过准确拟合圆弧找到汽车间隙面差测量所需的关键点，辅助间隙面差以及其他零部件圆度、同轴度的测量等等。

由于本研究所提出的方案目前仅用于标准件模拟汽车“四门两盖”小圆心角小圆弧进行测量，在下一步的研究工作中，笔者将针对汽车实车测量过程中的复杂情况进行改进。