叶片式真空泵转子组件的尺寸链分析与计算方法研究

刘胜园，叶华仁，李俊国，刘晓阳，刘振宇，孙世夺

（1.石家庄博安不锈钢设备有限公司，河北 石家庄 050035；2.马来亚大学 工程学院机械工程系，马来西亚 吉隆坡50603；3.河北科技大学 机械工程学院，河北 石家庄 050018）

0 引言

叶片式真空泵也称作旋片式真空泵，是一种容积泵，广泛应用于医药、食品加工、化工等领域，其工作过程中借助于旋转叶片在泵腔中连续运转将气体吸入并压缩后由排气口排出[1]。转子组件是叶片式真空泵的核心结构，其装配精度是响叶片式真空泵工作性能及其零部件的工作寿命的关键因素，叶片式真空泵在实际安装过程中主要采用调整法或者修配法装配，装配过程中往往需要经过多次试装，甚至拆卸、返工才能装配出合格产品，导致一次装配成功率低于50%，极大影响真空泵的装配质量和装配效率。因此，在转子组件装配前实现其装配精度的精确预测是提高转子组件装配质量及性能的有效途径，并为其零部件设计提供有力的参考基础。

装配精度预测在产品设计阶段或产品装配工艺规划阶段，对产品关键位置的装配精度进行预测的技术[2]。装配偏差传递路线搜索是装配精度预测的关键技术，主是通过分析装配体结构和装配方法，找出影响装配体关键位置几何特征之间相对位置及变动的公差项，包括基于尺寸链的方法[3，4]、基于变动几何约束的方法[5]等方法，Bjorke[6]提出使用数据化的尺寸链模型，为尺寸链技术的研究奠定了基础；江思敏等[7]研究了装配体组成零件之间的三维拓扑关系，建立零件配合关系图及配合关系矢量矩阵；Kuo[8]针对尺寸链中的组成环不满足正态分布的情况，通过累加计算每个组成环的方差、偏度系数和峰度系数等分布特性，获得封闭环的分布参数。

考虑到真空泵转子组件是通过尺寸公差控制其装配质量的主要公差项，对于这类结构尺寸链技术凭借较强的泛用性，在装配精度预测中最为常用[9]，并且尺寸链形成及分析是难点问题[10]。因此，对转子组件的装配结构和装配工艺进行分析，在此基础上，根据装配精度要求，基于最小传递路径实现转子组件的装配尺寸链的生成，并结合转子组件的装配工艺特点选用大数互换装配法进行尺寸链分析计算，获得尺寸链中各组成环的尺寸精度，以满足真空泵转子组件的装配功能要求和一次装配成功率。

1 装配尺寸链

1.1 尺寸链及其分类

尺寸链是将相互联系的尺寸按照首尾相连的顺序连接成一个封闭的尺寸组，尺寸链中的“尺寸”是广义尺寸，包括长度、角度和几何误差等尺寸，将这些尺寸分为组成环和封闭环，无论多么复杂的尺寸链，只有一个封闭环，其他尺寸为组成环[11]。通常按照尺寸链环的几何特征和所处空间位置，可将装配尺寸链分为四类：

（1）直线尺寸链是尺寸链的基本形式，也称作线性尺寸链/一维尺寸链，其主要特征是组成环与封闭环均位于同一平面上，且全部组成环平行于封闭环的尺寸链。

（2）角度尺寸链是全部组成环为角度尺寸的尺寸链，也包括几何公差中平行度、垂直度和倾斜度组成的尺寸链，其中全部组成环与封闭环形成公共角顶的封闭角度图形，是角度尺寸链中最简单的角度尺寸链。

（3）平面尺寸链是组成环与封闭环不平行，且位于一个或几个平行平面内。平面尺寸链分析计算过程中，通常采用投影的方法转换成直线尺寸链。

（4）空间尺寸链定义是组成环位于几个不平行平面内的尺寸链。空间尺寸链分析计算过程中，可将空间尺寸链投影→平面尺寸链→直线尺寸链，按直线尺寸链求解。

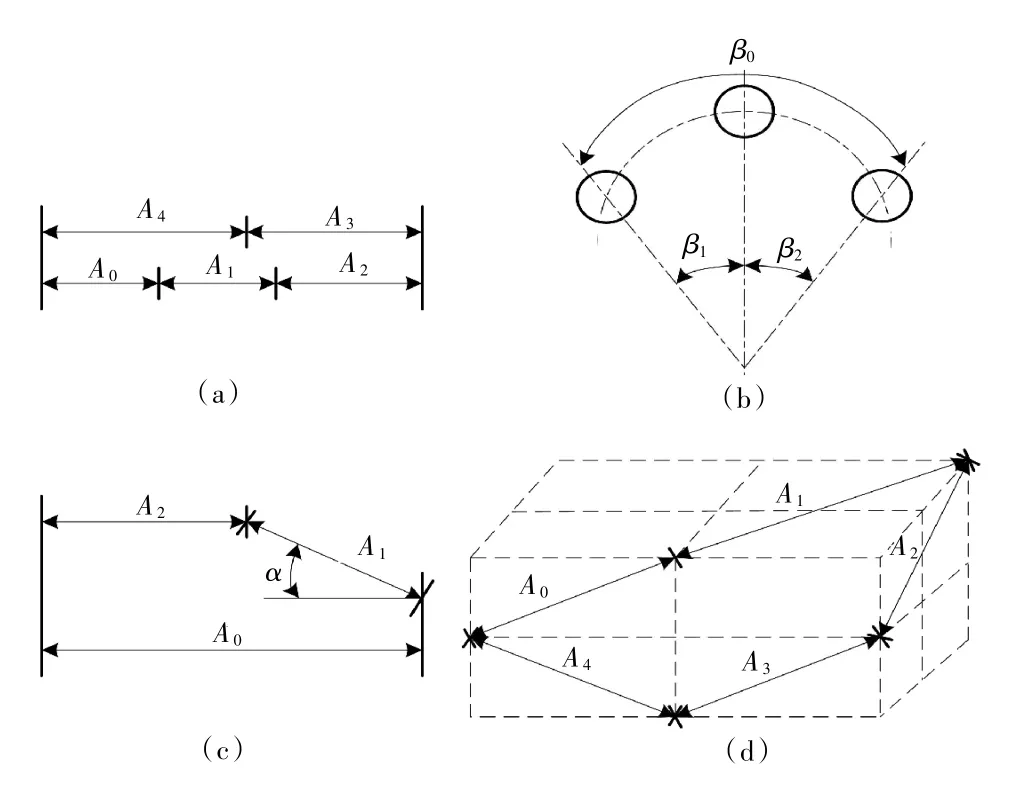
图1 装配尺寸链

1.2 装配尺寸链的建立

尺寸链中的组成环分为增环和减环，其中，将引起封闭环同向变动的组成环定义为增环，引起封闭环反向变动的组成环定义为减环，封闭环的大小与增环、减环有关，且当增环最大，减环最小时，封闭环最大；当增环最小，减环最大时，封闭环最小，所以有以下计算关系：

（1）封闭环公称尺寸＝增环公称尺寸-减环公称尺寸；

（2）封闭环上极限尺寸＝增环上极限尺寸-减环下极限尺寸；

（3）封闭环下极限尺寸＝增环下极限尺寸-减环上极限尺寸。

各组成环通常采用回路法对组成环判别增、减环，判断方法如下：

①确定封闭环：在装配尺寸链中，将装配之后形成的尺寸定义为封闭环，是产品上有装配精度要求的尺寸，如零件装配后的相对位置尺寸或保证相对运动的间隙等。建立尺寸链之前，需对产品装配和验收技术要求中规定的所有尺寸精度和几何精度要求项目进行分析，以确定封闭环；

②确定组成环：沿封闭环任意方向标单向箭头，依次找出相邻零件的尺寸，一环接一环，直到封闭环另一端为止，从而形成封闭的首尾相接的尺寸链；

③增减环的判断：与封闭环箭头方向相同的组成环为减环，与封闭环箭头相反的组成环为增环，如图2（a）所示；或者标注符号（+）（-）来表示增、减环，如图2（b）所示。

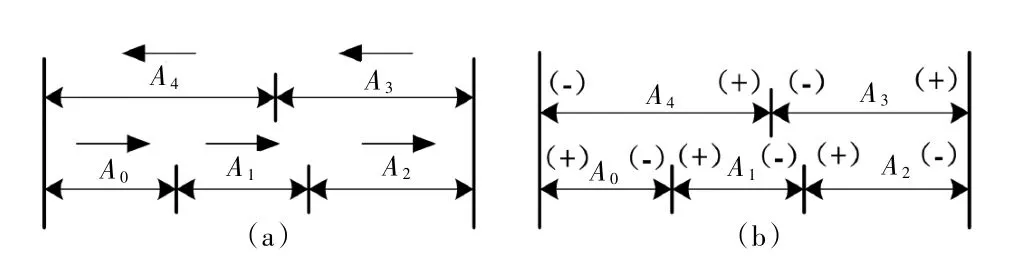
图2 组成环的增/减环判断

2 装配尺寸链分析与计算

基于互换性原则，转子组件拟采用互换装配法进行装配，即通过控制零件加工误差，而装配时不经任何处理，便可达到所需装配精度，分为完全互换法和不完全互换法。其中，完全互换装配法是装配过程对零件不挑、不修、不调，具有装配质量可靠，装配过程简单，生产率高等特点，但是装配零件难用经济精度加工，加工困难；不完全互换装配法又称大数互换装配法，其实质是将装配尺寸链中各组成环的公差放大，按经济的加工公差制造，使各零件容易加工，并降低制造成本，其特点是：装配时各零件不需挑选、修配和调整，而使绝大多数产品保证装配精度的要求，对于少量不合格品予以报废或加以修复；零件规定的公差较完全互换法大，有利于经济加工，装配简单方便。

因此，从装配的经济性角度出发，转子组件选择不完全互换装配法进行装配。不完全互换装配法是以一定的置信水平为依据，一般采用统计公差式计算，即当组成环尺寸符合正态分布，封闭环也为正态分布，如图3 所示。

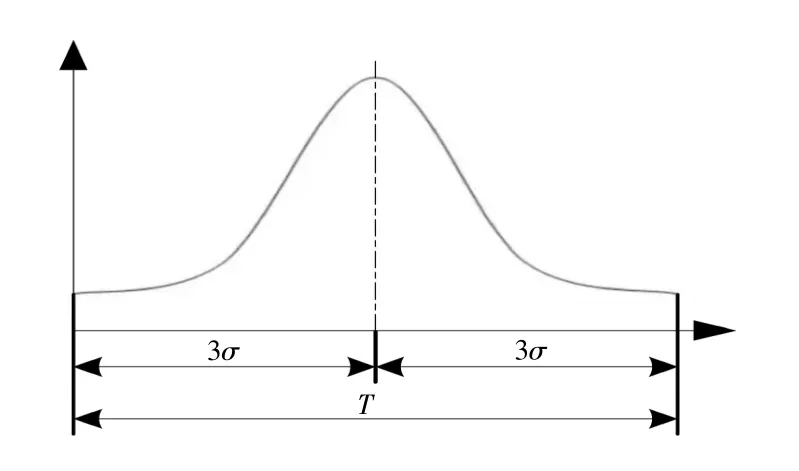
图3 正态分布图

不完全互换装配法存在以下特点：

（1）尺寸链各尺寸环的平均尺寸等于各尺寸环尺寸的平均值（即将非对称公差转换为对称公差AM＝±T/2），概率法平均尺寸：

（2）各尺寸环的尺寸公差等于各环尺寸标准差的6 倍（即T0＝6σ0，Ti＝6σi），其组成环和封闭环公差关系：

式中，相对分布系数k0取决于装配合格精度，当合格率p＝99.73%，k0＝1，当合格率p＝95%，k0＝1.5，合格率越高，k0值越大。因此，可得到各组成环的平均公差值：

其中，组成环中协调环公差如式（4）所示：

3 转子组件的精度分析与计算

3.1 转子组件的装配精度分析

为了保证真空泵的使用性能，设计人员在设计产品时，都规定了必要的合理的装配精度，其中，转子组件中转子、叶片与泵底之间的装配间隙A0就是其中最为关键的装配精度，如图4（a）所示。如果装配间隙A0过大，会导致真空泵的密封性能不好，影响真空泵的工作效率；如果装配间隙A0过小，甚致导致转子、叶片与泵底之间保持不住油膜，会造成转子、叶片与泵底之间迅速磨损，发热量增大，严重的可以造成真空泵出现“卡泵”现象，上述两种情况都是达不到产品性能要求的，即使勉强达到了也会因外界环境变化而不稳定，使得真空泵的寿命也会不长的。因此，在装配精度设计和实际装配过程中，需确保装配间隙A0取值合理。

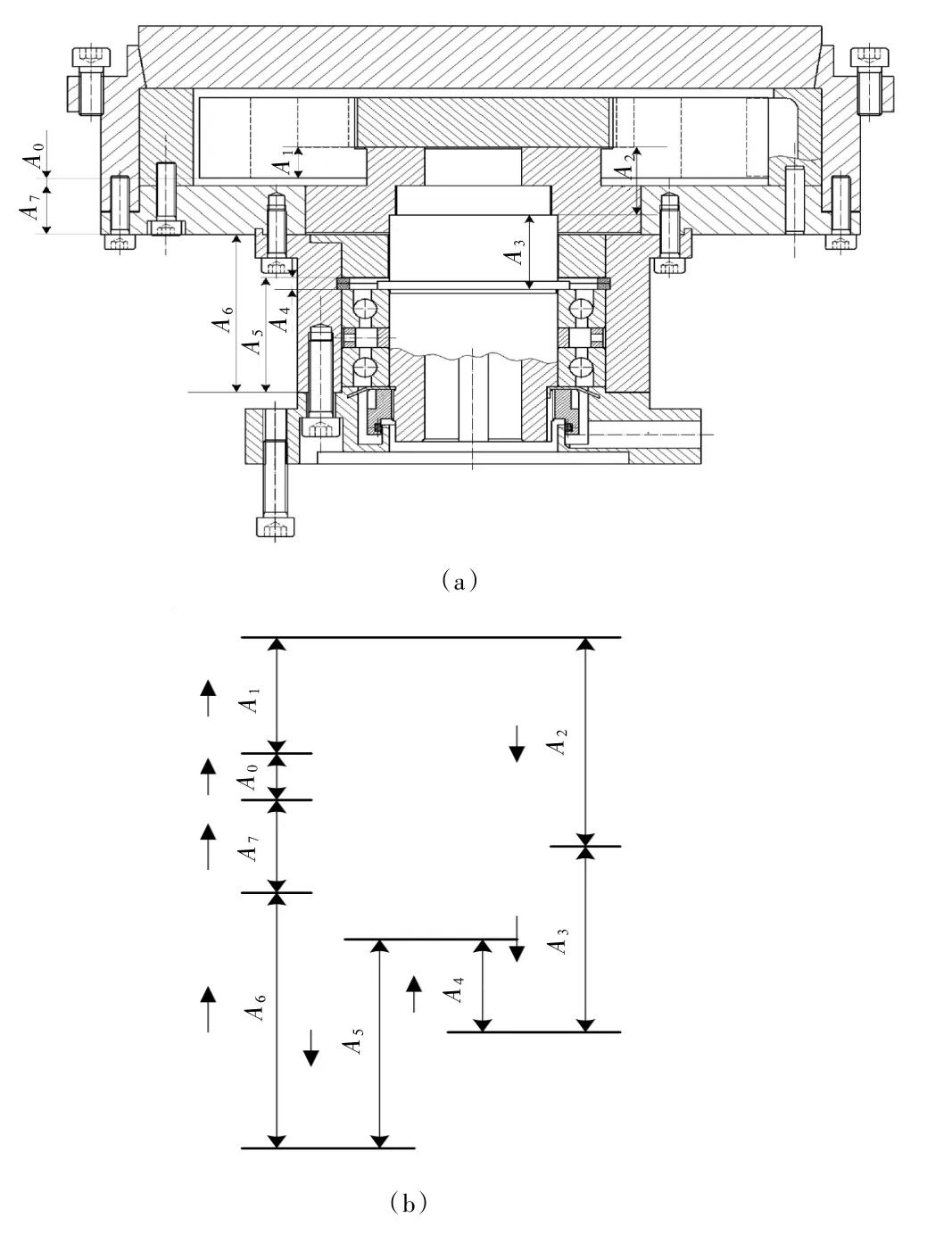
图4 转子组件的装配图及其尺寸链

3.2 转子组件的尺寸链建立与计算

对转子组件的装配结构进行分析，确定装配间隙A0为转子组件尺寸链的封闭环，装配精度要求A0＝。沿封闭环任意方向标单向箭头，依次找出相邻零件的尺寸，一环接一环，直到封闭环另一端为止，从而形成封闭的装配尺寸链图如图4（b）所示。装配尺寸链中组成环各尺寸为：A1＝50 mm，A2＝65 mm，A3＝38 mm，A4＝5.6 mm，A5＝58.6 mm，A6＝81 mm，A7＝25 mm，根据图4（b）中箭头的方向，可判断A1，A4，A6，A7为减环，A2，A3，A5为增环；基于不完全互换装配法，各组成环和封闭环都符合正态分布，设计转子组件的装配合格率p＝95%。

取合格率p＝95%，则k0＝1.5，代入式（3）得：

对各环的公差进行适当调整，结合转子组件的结构和装配工艺，选择A2为协调环，则TA1＝0.019，确定公差等级为IT6 级；TA3＝0.016，确定公差等级为IT6 级；TA4＝0.008，确定公差等级为IT6 级；TA5＝0.019，确定公差等级为IT6 级；TA6＝0.022，确定公差等级为IT6 级；TA7＝0.013，确定公差等级为IT6 级。

由式（4）得，A2为协调环公差为：

则取TA2＝0.019，公差等级为IT6 级。

采用入体原则[10]，各组成环的尺寸为：

协调环的中间偏差为：

通过对转子组件的装配结构进行分析以及选用大数互换装配法进行尺寸链分析计算，得到转子组件的尺寸链及各环尺寸精度分布，如图5 所示。在此精度下实现转子组件装配合格率p＝95%，可提高转子组件一次装配的成功率。

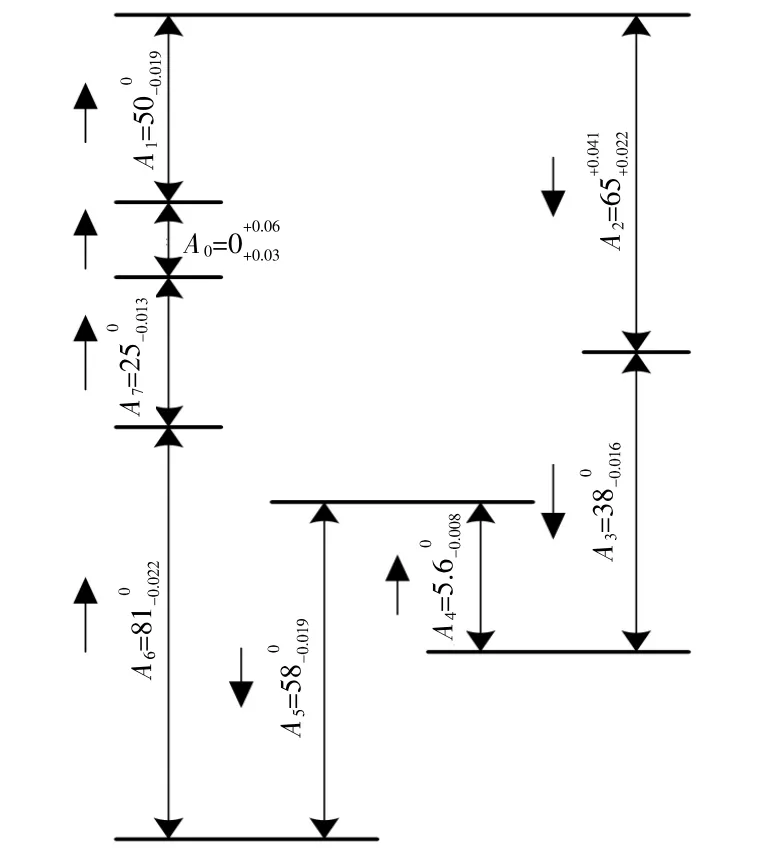
图5 转子组件的尺寸链及各环尺寸

4 结语

装配精度预测是保证真空泵符合质量要求的重要手段。结合某真空泵转子组件装配精度分析实例，根据真空泵转子组件的实际安装情况和装配工艺特点，选择不完全互换装配法进行装配精度分析，在满足装配合格率p＝95%的设计要求下，对影响转子组件中转子、叶片与泵底之间的装配间隙的装配尺寸进行分析并建立尺寸链，计算了尺寸链中组成环的公差和极限偏差，为真空泵转子组件装配公差分配提供解决方案和理论依据。