冲击波作用下沉箱式防波堤地基有效深度的计算

罗鑫健

(广东省水利水电第三工程局有限公司，广东 东莞 523710)

1 概 述

为了成功地对沉箱防波堤进行风险评估，了解结构在不同类型波浪袭击下的可靠性至关重要。文献[1]提出了沉箱防波堤的3级设计方法，称为“基于变形的可靠性设计”[1]。在这种方法中，沉箱的预期滑动距离是通过模拟计算结构，使用寿命期间滑动距离的统计平均值[2]。并对概率防波堤技术的现状进行了全面的回顾，它包括如何使用概率方法设计防波堤的指南，以及如何计算作用在防波堤和基础上的各种力的建议。沉箱式防波堤的基本运动形式包括振动、滑移和提离摇摆等[3]。根据沉箱的结构形式和作用力情况，沉箱以基本运动形式或基本运动形式的耦合形式运动。

在所有这些模型中，由特定波浪压力引起的位移假定在沉箱的整个寿命期间保持不变。Shimosak模型建立了沉箱式防波堤振动-滑移耦合运动数值分析模型，应用有限元模型对沉箱式防波堤的动力响应进行了计算，研究了防波堤的动力响应对有效波浪力的影响，提出了允许沉箱发生滑移运动的设计概念，以考虑沉箱倾斜对滑动距离计算的影响[4]。在这种方法中，需要对沉箱的最终倾斜角度进行假设，因为Shimosak模型没有提供估算的方法。利用简单土力学固结理论，可计算沉箱底部的沉降量，从而考虑了防波堤倾斜的计算。在Esteban模型中，一般来说，对于受到冲击波影响的沉箱防波堤，地基有效深度(dz)的计算对于正确计算土堆的变形至关重要[5]。通过物理模型实验，研究近破波作用下沉箱式防波堤的运动形态，并对上述数值分析模型进行检验，是有待开展的研究工作。

2 实验装置

所使用的波浪水槽(长15.3 m×宽0.6 m×深0.55 m)以及实验装置的布置见图1。采用1∶100的比例，在整个实验过程中，水槽中的水深保持不变，h=0.30 m。放置两个测波器测量波浪状况，一个在水槽中间，另一个靠近防波堤测量入射波高。两个测波器都连接到一个数字记录器上。对两种不同配置的测量装置重复实验：

图1 实验装置

第一种布局包括放置在碎石堆内3个不同位置的称重传感器(顶部、中部和底部，见图2)。在地基的顶部放置两个称重传感器，其中一个称重传感器的中心点距离柱脚0.5 cm，另一个距离柱脚1.5 cm。

图2 测量装置的第一种布局

第二种布置(图3)将所有的载荷单元放置在碎石堆的顶部，每个在彼此的1 cm内，以测量沉箱施加在碎石基础上的压力分布。

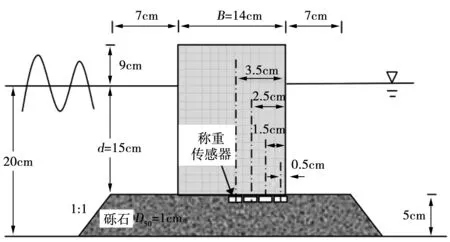
图3 测量装置的第二种布局

基础顶部的砾石被轻轻压实，使沉箱防波堤下的荷载细胞停留在水平面上。此程序也试图重现砾石地基在正常施工过程中所经受的压实。

沉箱单元由玻璃制成(高24 cm×长14 cm×宽20 cm)，并填充普通砂和金属砂，以获得与实际沉箱(ρ=2 000 kg/m3)相似的总体密度。在沉箱底部涂上一薄层水泥，使模型沉箱的摩擦系数与实际沉箱的摩擦系数相似[6]。所用基础材料由直径为10 mm的小角砾石颗粒组成。在所研究的沉箱侧面，放置另外两个“虚拟”沉箱，其具有更大的宽度B，以便只有所研究的沉箱可以被波浪移动。模型和模拟沉箱之间保持2 mm的间隙，以保证在试验过程中不会发生任何一侧的摩擦。

3 波浪条件

由表1可知，沉箱装置受到各种波浪条件的影响。试验中使用了规则波，在结果分析中，使用的数据仅包括在储罐中产生驻波之前记录的波浪。表1显示了给定造波机H的输入值和记录的入射H。对于非破碎波条件，输入参数与防波堤上记录的值之间存在明显的关系。但是，水槽的深度限制了波高，达到一定高度后，波浪将变形并开始破碎。因此，在第S4组之后，入射H不会发生显著变化，尽管波剖面变得越来越偏心，直到第S8组达到完全破坏。尽管由于波浪水槽的限制，一些试验组只能在有限的T范围内进行，但每组试验都是针对不同的T重复进行的。

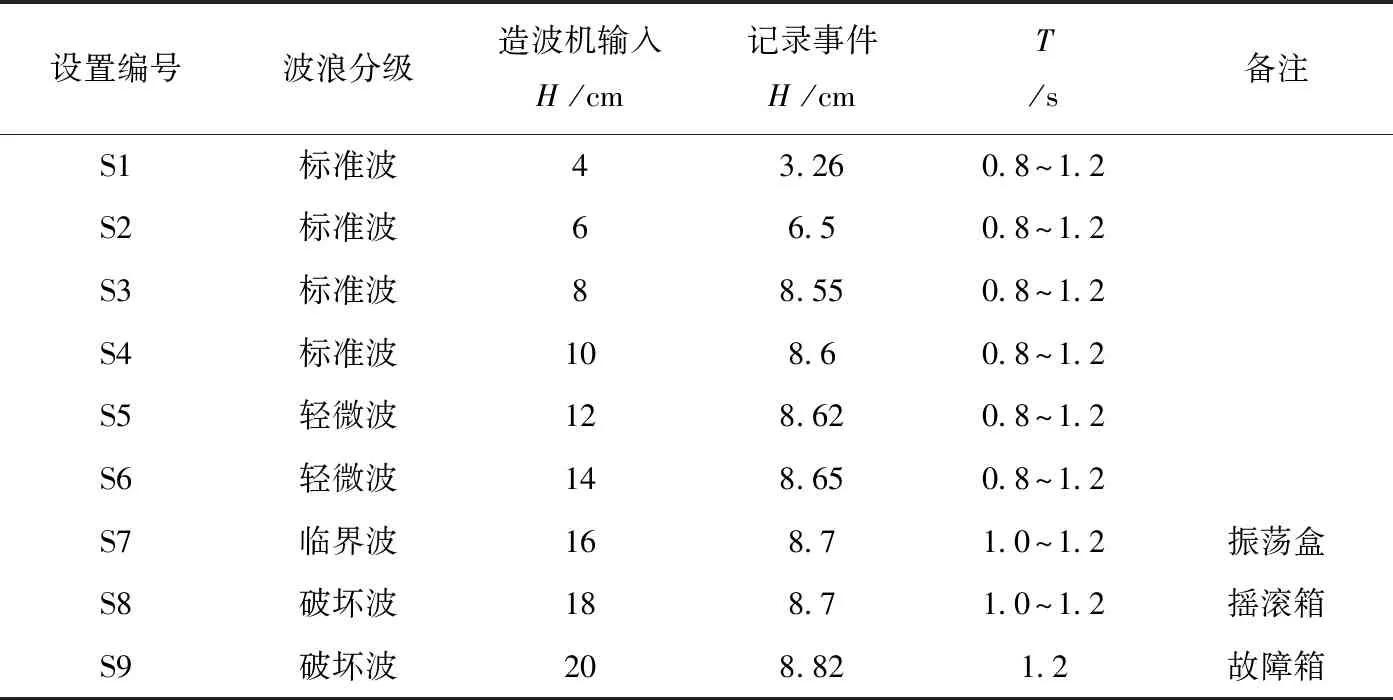
表1 波浪条件总结

每一组实验都是针对两种测量装置的布局进行的，见图2和图3。

4 实验结果

图4-图8显示出在靠近沉井脚跟不同位置的实验2号布局的碎石堆基础顶部的载荷。可以看出，在大多数荷载条件下，最大荷载不是发生在沉箱边缘，而是发生在距该边缘一定距离处。随着波浪变得更加偏心，可以观察到荷载的明显演变，驻波的正弦曲线(图4)让位于更快速和寿命更短的初始荷载，然后是准静态荷载分量(图5)。初始冲击载荷的峰值随着波浪形状接近“完美”破碎的形状而增加(图5-图6)。当沉箱开始接近倾覆平衡位置(图6)，倾覆力等于抵抗力的点。最终沉箱开始在其背部部分岩石上，因此脚跟上的载荷比地基的其他部分的载荷大(图7)。一旦达到完美的破坏，沉箱上的力远远大于它所能承受的，基础的大部分与地面失去接触，沉箱有效地晃动其后跟(图8)。因能量高于S9组的波浪使沉箱倾覆，因此在此条件下停止试验。

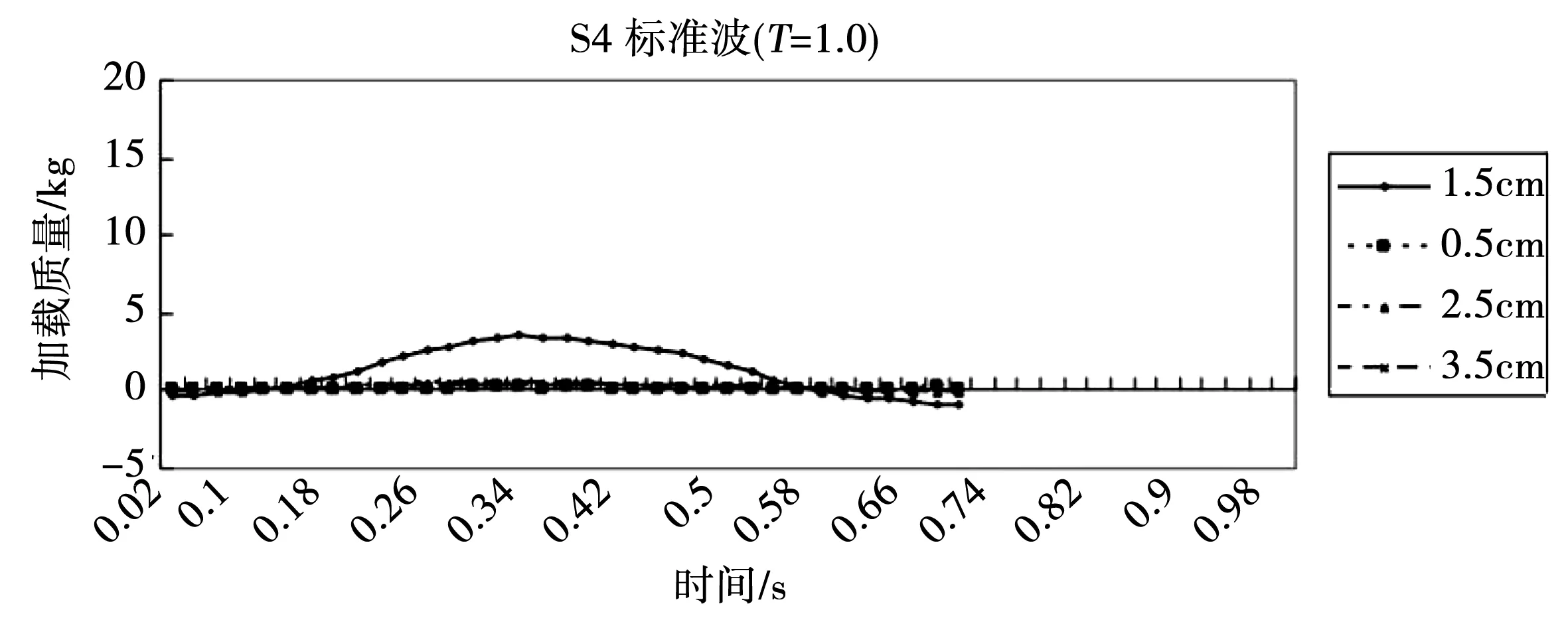
图4 Set S4的加载时间历史记录

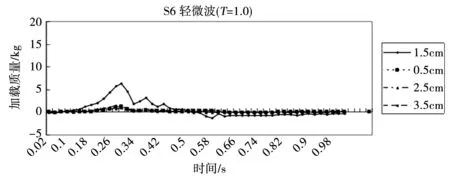
图5 Set S6的加载时间历史记录

图6 Set S7的加载时间历史记录

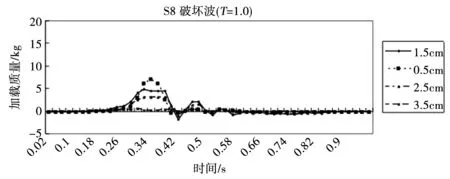
图7 Set S8的加载时间历史记录

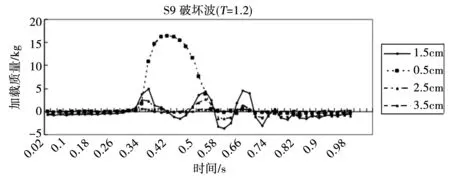
图8 Set S9的加载时间历史记录

用Boussinesq理论分析数据，最大荷载不发生在沉箱边缘，而是发生在边缘之前的一定距离处。当沉箱开始接近倾覆平衡位置(即E倾覆力等于抵抗力的点)，最后沉井开始在其背部的部分岩石，因此在脚跟的负载变得比基础其他部分的负载大。根据传统的土力学理论，在宽度为n的条形区域上，由于压力从零到q线性增加，X点的垂直应力(σz)以角ζ和λ以及长度R1和R2表示，见图9。

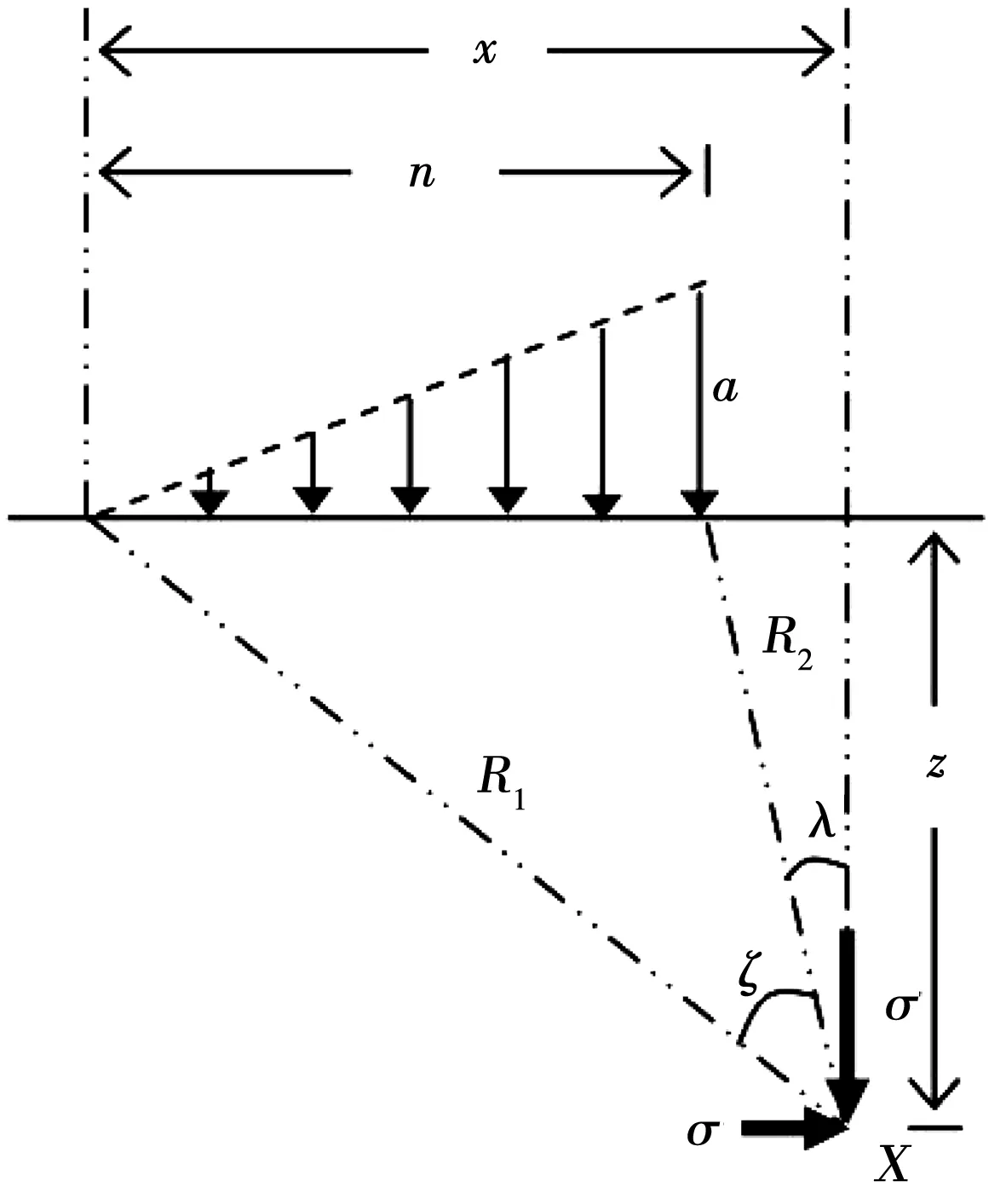
图9 条形区域上线性增加的压力产生的应力图

(1)

然而，在分析地基上的荷载时，必须注意使用适当的n和x值。在当前的实验中，基础内的载荷单元位于距防波堤的脚跟处0.5 cm处，但最大载荷的位置在实验之间不同。对于条件S1-S7，其位于m=1.5 cm处；而在S8和S9中，其位于m=0.5 cm处。见图10。

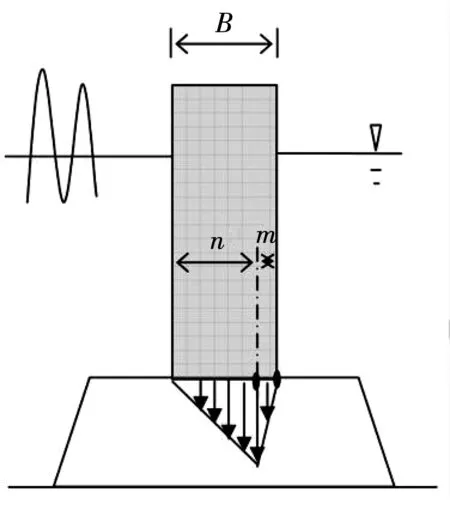
图10 地基荷载示意图

从图11可以看出，由Boussinesq理论计算的值与深度2.5 cm处的实验值之间有很好的相关性，尽管它倾向于高估更大深度处的载荷(图12)。其原因可能在于波浪作用于土壤的快速加载和卸载循环，这与经典土力学理论形成对比，后者处理的是长时间发展的荷载。

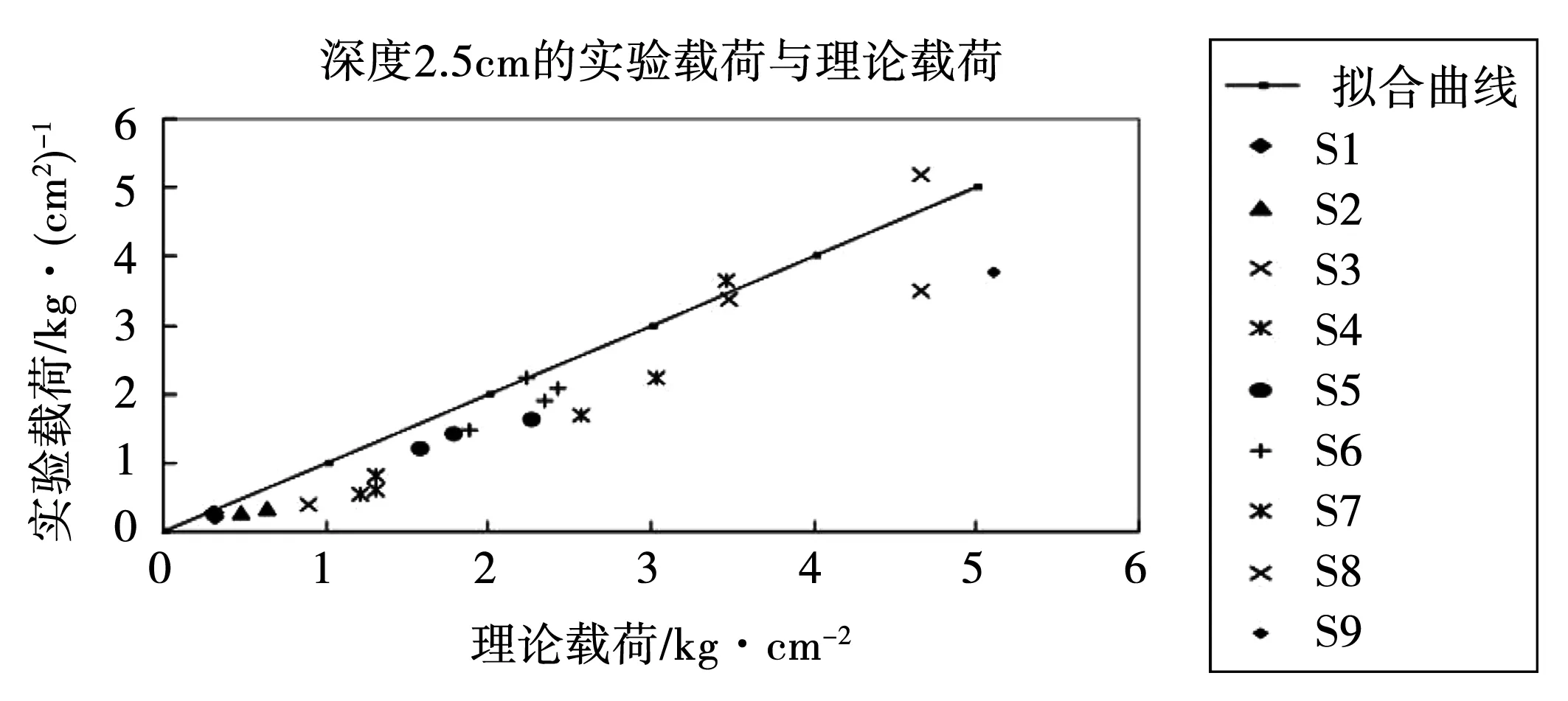
图11 深度2.5 cm处实验载荷和理论载荷的比较

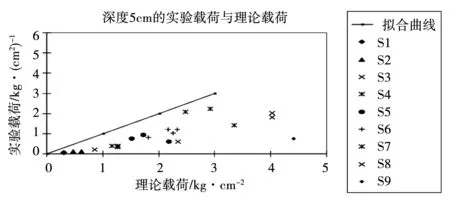
图12 深度5 cm处的实验荷载和理论荷载的比较

因此，通过使用Boussinesq理论，可以估计地基顶部区域的荷载。当根据这一理论计算荷载随深度的垂直变化时，大部分荷载似乎集中在基础顶部长1 m的土带内，见图13。这似乎与感知的破坏机制非常一致，其中大部分荷载将被地基的塑性变形所吸收。

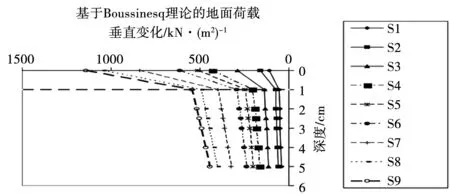
图13 根据布辛内斯克理论的垂直荷载变化

对试验结果的讨论对于大多数沉箱防波堤设计，使用深度1 m作为基础的有效深度似乎是足够的。主动深度取决于波浪施加到地基上的力和地面的承载能力，而这又取决于地基的孔隙比。虽然在冲击波的情况下，深度1～2.5 cm的压力可以超过500 kN/m2，但地基的承载能力很可能超过这个数量。这是合理的，因为压实过程中，基础是在防波堤施工期间，由于沉箱的自然沉降通过低强度波作用之前的高强度事件波事件。根据Boussinesq理论，这两个过程很可能将砾石固结成可以被称为中密度的层，它可以承受200～600 kN/m2。然而，施加到地基上的压力也是宽度B的函数。如果设计长宽沉箱的目的是承受非常高的入射波浪力，那么在深度超过1 m时，这种大浪产生的压力可能远远高于500 kN/m2。因此，在这种情况下，将导致更大的dz。见表2。

表2 假定承载力值

因此，对于高宽度的沉箱，建议不要使用dz=1 m，而是使用式(1)计算整个护道的压力，从而计算基础的有效深度。由于dz基于地基承载力，而地基承载力又取决于孔隙比，因此dz不是一个常数，而是根据砾石的固结程度动态变化的。因此，在防波堤建造后不久，一定的H波将调动更大的dz，比沉箱经受了一定数量的风暴后还要多。在将目前的实验结果应用到实际设计中时，必须牢记发生尺度畸变的可能性。

目前的实验是在1/100的比例下进行的，因此得到的结果可能与原型情况下的结果有很大的偏差。整个地基上荷载的测量精度也被质疑。尽管采取了一切措施确保设备正确放置，各种构件(沉箱、砾石、称重传感器)始终保持接触，但由于荷载性质和碎石堆中发生的变形，这并非总是可能的。由于碎石堆内颗粒的位移，测量装置与顶部颗粒之间的接触经常丢失，导致没有记录载荷。此外，由于这些变形，在一个波通过后，测量装置并不总是返回0。因此，有必要谨慎地看待这些结果，尽管对每一个结果分别进行了分析，试图找出并消除这些问题，但有可能其中一些结果不能准确反映地面的实际压力。根据分析数据判断，这可能导致某些负载的误差高达10%左右。此外，在将本试验结果应用于原型防波堤时，必须考虑砾石形状对荷载传递的影响。目前的实验使用的是大小相当恒定的有棱角的砾石，其形状可能与实际建筑中使用的颗粒相似，通常是粉碎或爆破较大尺寸颗粒的结果。然而，圆形颗粒的特性与此略有不同，在实际设计中，应注意将结果应用于此类砾石。

5 结 论

室内试验表明，采用传统的Boussinesq理论可以近似地计算出沉箱防波堤在基础顶面上施加的压力。利用这一理论很可能出现大部分变形发生在一个狭窄的条带深1 cm的基础上，因此这个值被视为主动深度的基础上计算的垂直位移沉箱。但是，在确定该值时必须注意，对于与本试验中研究的沉箱截面差异很大的截面或荷载，最好使用提供的公式计算深度，而不是使用简化的1 cm值。这一结果在广州市珠江堤防西航道左岸鸦岗文笔水闸至石井水泥厂段达标加固工程沉箱式防波堤施工得到了验证，并证明了用简单土力学理论可以评价防波堤毛石基础中的竖向变形。