洪水预报中滞洪区的非线性模型预测控制研究

李发孝

(江西省九江市庐山市水利局，江西 九江 332000)

1 概 述

对水资源中的水工建筑物进行监控的最常用技术是明确操作规则的定义。例如，由于水库水位[1]和环境目标，水库的最小释放量，基于参考位置水位的滞洪流域运行[2]。这些操作规则通常与用于控制现场所需变量的二级控制器一起提供，即用于维持堰上游水位的PID控制器[3]。

上述概念一般仅适用于较小的水利系统，对于较大的系统，其应用将变得非常复杂。在这种情况下，运行规则和水系统可能表现不出期望的反馈效应，导致整个系统的仅能达到次优控制。近年来，将模型预测控制(MPC)应用于堰坝和水电站的监控中，较为成功地解决了这一问题。本文提出一种用于复杂河网水工建筑物控制的一般非线性MPC方案，并介绍了NMPC在控制两个滞洪流域的几个水工建筑物河流分叉点流量分布方面的实际应用。

2 非线性模型预测控制方案(NMPC)

假设对感兴趣的系统应用了空间图式，水资源系统的模型可以用以下一组通用的非线性常微分方程来描述：

(1)

其中：x∈Rl为系统状态向量；u∈Rm为受控变量的向量；d∈Rn为扰动向量；l为状态数；m为控制变量数；n为扰动数。

受式(1)和p附加不等式约束：

gi(x,u)≤0,i∈I={1,…,p}

(2)

在显式时间步进方案的假设下，将非线性常微分方程(1)的集合转换为离散时间系统，并得到：

xk+1=f(xk,uk,dk)

(3)

其中：k为时间步长索引。

所得到的最优控制问题(2-3)由非线性规划方案SNOPT求解。

3 内部模型

一维河网中的明渠水流用质量(连续性)和动量守恒的德圣维南方程描述。连续性方程为:

(4)

动量方程的非保守形式定义为:

(5)

其中：A为润湿面积；Q为流量；qlat为单位长度侧向流量；h为水的高程；v为水流速度；g为重力加速度；m为水力半径；C为谢才系数；cf为无量纲底部摩擦系数。

通过忽略式(5)中的惯性和对流项，可导出运动学波动方程。通过额外代入v=Q/A，并在交错网格上应用空间模式化，在此网格上将这些节点的距离定义为Vx，则有：

(6)

式中：C、A、m可表示为平均水位(hup+hdown)/2的函数。

如果两个蓄水节点之间存在水工建筑物，则流量方程(6)可替换为水工建筑物的一般方程：

Q=fstructure(hup,hdown,dg)

(7)

其中：dg为闸门或堰的设置。

连续性方程(4)的数值解通过前向欧拉法计算完成，结果如下：

(8)

其中：k为时间步长。

通过代入s(h)=A(h)Δx，乘以Δx，忽略侧向流量，用蓄水量s代替水位h，引入方程(6，7)，可以将方程(8)转化为节点水位的水量平衡：

(9)

其中：s为节点上的存储；i为连接到存储节点分支的索引。

预测范围内最优控制问题的拉格朗日形式可写为：

(10)

式(10)中，将每个离散时间步长的系统方程定义为最优控制问题的独立等式约束。

4 案例研究

本文研究案例河流为江西省九江市长江流域某支流，其分岔点的流量直接决定该河流下游各支流流量分布，因此对九江市的水资源管理有着重要影响。通过介绍该流域某支流用于洪水预报系统中作为试点实施的NMPC设置，控制S01处的水工结构来控制中低流分岔点的流量分布(图1)。通过运行两个预计的滞洪区的5个进水口和出水口结构(S02-S06)，用于在洪水事件期间抑制洪峰。

图1 运动波模型布置图

本文选择从2007年10月至2008年12月的时间段进行模型校准。通过调整每个流量支路的水位相关粗糙度，直到所选仪表上每小时观测水位与模拟水位之差的均方根误差(RMSE)达到10 cm左右。表1给出校准的一整套性能指标。

表1 用于模型校正的性能指标(2007.10-2008.12)

图2(a)中，水位在各工况之间转换，从完全关闭闸门，设定点不能维持水位的低流量(1)，到水位完全稳定在设定点的中高流量(2)，闸门完全打开且闸门上游和下游水位平衡的更高流量(3)。图2(b)是一个小洪水波的衰减过程。在第(1)阶段，滞洪区域的入口结构仍处于非活动状态；在第(2)阶段开始排水，将H01的水位保持在12.75 m a.s.l.的水平；第(3)阶段进水闸门再次关闭，直到水通过第(4)阶段的出口结构从滞洪区域中排出。

图2 水位在各工况之间的转换过程

图3显示了1个结构(120维数)和6个结构(720维数)的优化问题都实现了这一目标。对应用程序的分析(表2)表明，这是因为与总CPU时间相关的模型执行比例较高，显示了相当大的潜力，甚至可以通过实现如隐式时间步，进而加速NMPC的运行。

图3 多个MPC执行、单个控制结构(红色)和并行优化6个控制结构(蓝色)的计算时间

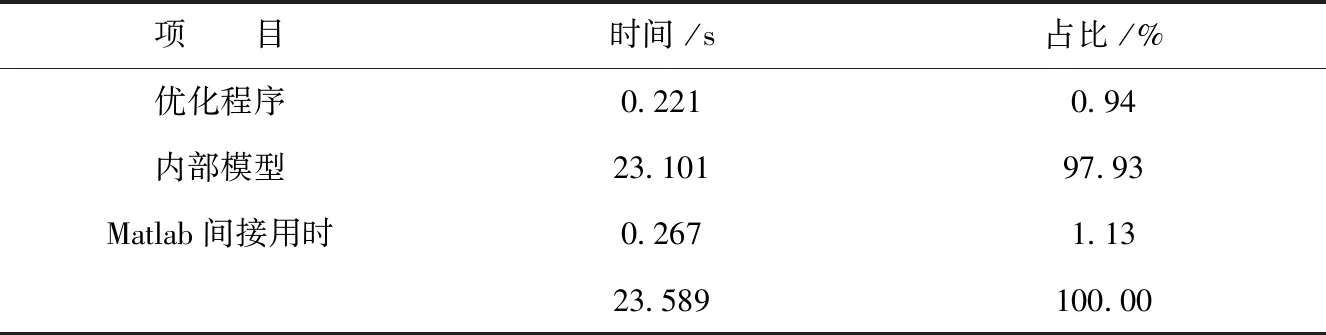
表2 单个MPC应用程序的CPU配置文件，包括6个水工结构并行优化用时

5 结 论

本研究提出一种支持水工建筑物运行决策的非线性模型预测控制方案，并将其应用于复杂河网的滞洪流域控制。通过将模型与九江市长江流域某河流实测数据对比研究后，验证了模型的准确性。由于本文提出的框架是通用的，该模型允许直接集成任意过程模型和控制目标，适用于水资源的各种其他应用，如水电站或灌溉系统的梯级控制，为水资源的合理控制及有效利用提供一定的参考。