地铁电源模块故障分析及预测方法

2022-03-01陈秉智李永华

东北大学学报（自然科学版） 2022年1期

宫琦, 陈秉智, 李永华, 夏清

(1. 大连交通大学机械工程学院, 辽宁大连 116028; 2. 大连交通大学机车车辆工程学院, 辽宁大连 116028)

牵引逆变系统是地铁车辆牵引系统的关键部件,是车辆电气系统的重要组成部分,该系统运行品质的优劣对车辆的安全性、旅客的乘坐舒适性有直接影响,它的故障会导致车辆的停运、经济损失，甚至负面的社会影响[1-2].牵引逆变系统主要由线路接触器、预充电电路、滤波电抗器、支撑电容、放电电阻、功率模块、牵引控制单元、电源模块和各类传感器组成.电源模块负责给各控制板卡、电压电流传感器、绝缘栅二极晶体管(insulated gate bipolar transistor,IGBT)驱动板等供电,因此电源模块的故障将直接导致牵引逆变系统、空调系统、列车网络无法正常工作.

牵引逆变系统为车辆运行提供牵引力和电制动力,其运行的可靠性、使用寿命直接影响整个车辆的总体水平[3-4].近年来,学者们对牵引逆变器IGBT的老化状态监测、故障率和寿命预测研究比较多[5-6],对电源模块的故障维修、故障预测研究很少.文献[7]对长沙地铁24 V电源模块的烧损故障进行了原因分析,并制定了相应的整改及预防措施,避免了类似故障的发生.

近年来,诸多学者对故障预测方法开展了有价值的研究.目前,国内外应用比较广泛的故障预测方法主要有四大类:基于知识的方法[8-10]、基于模型的方法[11-12]、基于数据的方法[13-14]和基于融合技术的方法[15-16].数据驱动法是故障预测方法的核心,是比较实用的故障预测方法.基于融合技术的方法是将基于模型的方法和基于数据的方法相融合,既可以发挥二者的优势和特点又克服了单一方法的局限性,从而获得更高的预测精度.

由于电力电子电路中的主电路元器件较易出现故障,而主电路又是完成功率变换的核心功能电路,所以对电力电子电路主电路的故障预测研究吸引了许多学者的关注.目前,对电力电子电路的故障预测主要从预测对象和故障预测算法两方面进行研究.

针对预测对象方面研究的重点多集中于器件级的故障预测,比如电容[17-18]、MOSFET[19]和IGBT[20]等故障高发元器件以及DC/DC变换器的电路级故障预测.器件级预测主要是通过分析这些故障高发器件的失效机理构建器件的失效模型或者监测器件故障特征参数的细小变化,完成器件的健康状态或者剩余寿命的评估.电路级故障预测主要是从电路整体性能退化方面预测,不关注内部元器件的退化状况.在实际应用中,功率变换器以模块形式存在,如果发生故障即可整体更换,所以电路级故障预测更具有实际工程意义.

针对故障预测算法方面研究的重点多集中于基于数据的方法.文献[21]基于等效串联电阻值和电容值的退化特征参数运用最小二乘支持向量机、BP神经网络和GM(1,1)模型实现变换器输出电容故障值预测.文献[22]选取输出功率、输出纹波电压和电感电流作为故障特征参数,采用隐马尔可夫模型实现开关电源变换器的故障预测.文献[23]提出了基于平均电压预测的级联H桥多电平逆变器广义开关故障诊断方法.由于电力电子电路失效物理模型构建困难,而电路状态信息获取容易,因此,基于数据方法的电力电子电路故障预测研究的较多.

为提高预测精度,解决电力电子电路故障预测过程中系统模型繁杂、建模难、故障特征参数和故障阈值确定困难等难点,需朝着融合技术的发展方向努力,比如兼顾多种算法的优点,将多种算法融合为一个新的算法,以提高故障预测的准确性.

基于此,本文针对某地铁车辆电源模块的烧毁故障,通过现场和试验室测试进行故障原因分析,提出整改措施并进行可行性验证.将灰色理论、傅里叶级数、马尔可夫理论与新陈代谢4种方法的思想相融合,提出一种新的故障预测模型.以地铁车辆牵引逆变系统电源模块故障次数数据进行算例分析,结果表明,本文所提模型较大程度地提高了预测精度.

1 基于试验与仿真的电源模块故障分析

某地铁车辆在服务运营初期,一个月内多次出现牵引系统不在线的情况,根据技术人员的维修,发现牵引系统不在线的原因是牵引控制单元机箱中供电电源模块烧毁,因此,解决此问题的关键是解决电源模块故障.该电源模块的主要功能是将DC110 V电源转化为DC15 V的电源输出供给牵引控制单元机箱使用,主要组成为DC110 V转DC15 V的模块(功率为200 W)、电阻和电容等元器件.电源模块烧毁的可能原因有:模块内部原因、外部供电有浪涌、机箱温度过高.本文通过试验及仿真进行故障原因的分析.

1.1 试验分析

1) 现场测试排查.通过测温度和测电流方式进行现场测试.在机箱外壁、内壁、电路板、电源模块、散热片上,通过贴温度贴的方式进行现场温度测试.列车运行10 d后,进库记录温度,温度测试显示,电源模块的最高温度为65 ℃,没有超过电源模块的受限温度115 ℃;对现场的牵引控制单元机箱供电,通过示波器抓取电压波形,未抓取到浪涌脉冲的情况,因此初步排除机箱温度过高和外部供电浪涌原因导致的模块失效.

2) 试验室测试排查.①采用接触式热电偶法进行带载温升测试.在试验室环境温度20.56 ℃条件下,选用T型热电偶,利用点胶法,将温度记录仪的探头胶固在电源模块表面,对其进行带载温升测试.该电源模块功率200 W,外接负载功率75 W,模块的受限温度为115 ℃,接通电源,待热稳定以后对温升进行测量,测试结果为 37.82 ℃,未超出模块受限温度.②浪涌测试.雷击浪涌测试是一种传导抗扰度测试,主要是通过传导的方式把浪涌干扰信号注入到被测装置中,以考验被测装置是否具有一定的抗浪涌冲击能力.浪涌试验台主要包括雷击浪涌信号发生器和耦合/去耦网络.雷击浪涌信号发生器是整个浪涌测试系统中至关重要的元件,负责产生雷击浪涌的波形.耦合网络主要是把雷击浪涌信号送到被测装置中,并确保被测装置的供电电压不能逆向流入组合波发生器,或者对被测装置与其他装置之间的通信没有任何影响;去耦网络是为了保证雷击浪涌信号不能直接进入网络后端,从而有效地保护供电电网或其他装置,并防止雷击浪涌信号分压致使输入端不符合测试要求.

按照GB/T17626.5—2008标准,在室温22 ℃、相对湿度38%、大气压力101.7 kPa的环境条件下,利用浪涌试验台对电源模块进行浪涌抗扰度试验.试验条件及试验结果见表1.

由表1可知,电源模块通过雷击浪涌测试,符合要求.

表1 雷击浪涌试验条件及试验结果

1.2 仿真分析

为了防止电源模块工作时温度过高而影响其使用性能甚至烧毁,因此电源模块装有翅片式散热器,其结构示意图如图1所示,其几何参数见表2.运用数值计算仿真分析方法对电源模块散热器进行温升计算.按照表2中给出的结构几何参数,利用ANSYS-ICEPAK流体分析软件建立散热器的热模型，并进行网格的划分、边界条件的设置以及求解计算.对边界条件进行设置：速度边界是入口为通风机冷却空气,平均流速1 m/s,环境温度为20 ℃,出口为压力出口;热边界为将电源模块的功耗200 W作为热源施加在基板面上,各部分材料的导热系数如表3所示.散热器温度分布云图如图2所示.

由图2可知,电源模块散热片最高温度为59.08 ℃,在电源模块正常工作受限温度115 ℃范围内.

1.3 整改方案及可行性验证

基于上述试验与仿真的分析结果,确定电源模块烧毁是模块内部原因导致,需进一步加强电源模块的电磁兼容性和保护措施,于是提出以下整改方案并进行了可行性验证.

1) 虽然雷击浪涌测试通过,但为了电源模块具有更好的电磁兼容性,在电路板输入端焊接CG3.1/1100 V气体放电管,按照IEC60950标准,使用摇表进行绝缘测试和使用耐压仪进行耐压测试,均通过测试.

2) 为保护电路板不出现烧毁的情况,电路板上需要有5 A电流的保护值,选择VF477-P熔断器,该器件采用插座形式,在不用更改PCB的情况下,在原来防反二极管的位置直接焊接该熔断器,解决电路板烧毁问题.焊接后进行短路试验,试验结果是熔断器瞬间断路,对电路板起到有效的保护作用.

图1 散热器结构示意图Fig.1 Structure of radiator

表2 散热器主要的几何尺寸参数

表3 材料导热系数

图2 散热器温度云图Fig.2 Temperature contour of radiator

经过整改,将10块电源模块进行实车运行测试,运行2个月,未出现烧毁情况.电源模块运行的稳定性直接影响着牵引系统的状态,为保证运营需要,需对牵引逆变系统电源模块的故障进行预测.

2 新陈代谢-改进的灰色模型

本文将灰色理论、傅里叶级数、马尔可夫理论及新陈代谢4种方法相融合的组合模型对电源模块故障进行预测.该方法首先采用传统的灰色模型预测结果为基础,利用傅里叶级数对序列残差进行一次修正,然后基于马尔可夫理论建立状态转移概率矩阵对序列残差进行二次修正,最后融入新陈代谢的思想,将已预测修正的结果作为新数据加入,剔除旧数据,进而预测下一时刻数据.具体建模流程如图3所示.

图3 建模流程Fig.3 Modeling process

2.1 灰色模型

灰色理论以部分信息已知、部分信息未知的小数据、贫信息不确定性系统为研究对象,通过生成和开发已知信息,提取价值高的信息,对系统进化规律进行正确的描述,从而实现系统进化规律的定量预测.本文使用最广泛、应用最多的灰色均值模型,其建模原理如下:

设原始数据序列X(0)={x(0)(1),x(0)(2),…,x(0)(n)}，n为数据个数,则X(0)的级比为

(1)

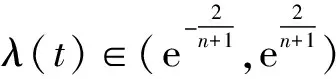
(2)

(3)

式中:

(4)

将a，b代入式(2)可得灰色均值模型的时间响应函数为

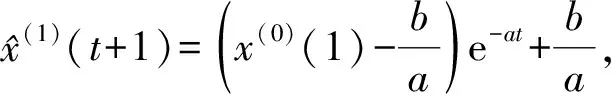
t=1,2,…,n-1 .

(5)

进行累减还原得

t=1,2,…,n-1 .

(6)

2.2 基于傅里叶级数的残差修正

当原始数据离散程度较大时,灰色均值模型预测精度明显下降,在进行长期预测时由于灰度不断叠加,可能产生较大的误差,因此借助傅里叶级数强大的降噪能力对灰色均值模型的残差序列进行修正,以提高预测精度.具体步骤如下:

1) 求残差序列.

2) 求残差序列的傅里叶系数.

残差序列可近似用傅里叶级数展开式表示为

(7)

将式(7)转换成矩阵形式为

E≈PFCF.

(8)

式中:

CF=[a0,a1,b1,…,akF,bkF]T为残差的傅里叶系数向量;E=[e2,e(t),…,e(n)]T为残差向量.

根据最小二乘法可以求得

(9)

3) 对灰色均值模型进行修正.

将求得的傅里叶系数向量CF代入式(7),即可求得EF(t),从而获得修正后预测值为

(10)

2.3 马尔可夫预测模型

牵引逆变系统电源模块是可维修的,但不能修复如新,因此故障次数的变化具有随机性,而马尔可夫模型可以改善这种“随机性”,因此本文采用马尔可夫预测模型在基于傅里叶级数的残差一次修正的基础上进行二次修正,以进一步提高预测精度.具体建模原理如下:

Ei=[εi1,εi2](i=1,2,…,k) .

(11)

式中,εi1，εi2分别为状态区间的上限和下限.

则一步状态转移概率矩阵为

(12)

(13)

式中:Mij为状态经过k步转移到状态Ej出现的次数;Mi为状态Ei出现的次数.由马尔可夫理论,n步状态转移概率为一步状态转移概率矩阵的n次方,即

(14)

转移概率预示着状态转移的发展趋势,可用来预测未来状态.当使用k步状态转移矩阵时,马尔可夫链中前k个时刻的数据位于状态E1,则p(k)的第一行向量被采用.若k步转移过程就需要k个转移概率向量,待预测的残差状态概率为k个向量的和,向量元素为γ1,γ2,…,γn,则待预测的残差修正预测值为

EM(t+1)=τ1ε1+τ2ε2+…+τnεn

(t=1,2,…,n) .

(15)

式中:εi为状态区间中心；τi为状态的权重，

τi=γi/(γ1+γ2+…+γn) .

(16)

则经过马尔可夫二次修正后的灰色均值模型预测结果为

(17)

2.4 新陈代谢模型

随着系统的发展,采用更能反映系统当前特征的新数据,剔除离预测数据较远的陈旧老数据,实现新陈代谢,可以更精确地对未来数据进行预测.因此本文采用新陈代谢模型对下一时刻的故障进行预测.

3 算例分析

目前,该牵引逆变系统在某市地铁车辆已运用8.5年,对故障排除后的电源模块的故障次数跟踪统计了8.5年,对8.5年的故障次数数据进行预测.从2012年1月某牵引逆变系统投入使用开始至2020年6月对128个该系统的电源模块样本进行了故障次数统计,见表4.

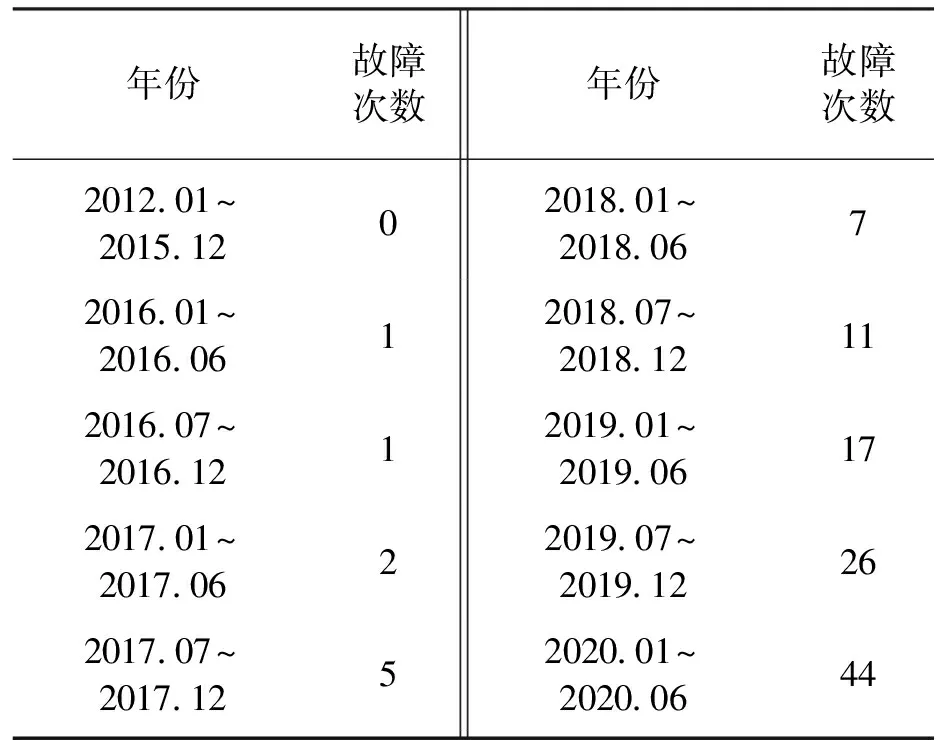
表4 电源模块故障次数

表4中从2012年1月至2015年12月该电源模块未出现过故障,从2016年1月该电源模块使用第5年开始，由于模块性能退化原因开始出现故障,因此样本数据从2016年1月出现故障开始选取,采用本文提出的方法研究该电源模块性能退化规律,预测故障次数,为维修策略的制定提供参考依据.

3.1 建立灰色模型

以表4中提供的2016年1月至2018年12月的6个故障次数数据作为原始序列,2019年1月至2020年6月的数据作为预测使用,即X(0)={1,1,2,5,7,11}.根据式(1)求X(0)级比,得到

λ(t)={1,0.5,0.4,0.714 3,0.636 4}.

(18)

λ(t)中的大部分数据未在(0.751 5,13 307),因此需要对数据序列X(0)进行预处理,本文选用开4次方的方法对数据进行预处理,得到处理后的数据序列为

X(0)′={1,1,1.189 2,1.495 3,1.626 6,1.821 2} .

(19)

由X(0)′生成一次累加序列X(1)={1,2,3.189 2,4.684 5,6.311 1,8.132 3},根据式(2)～式(4)计算可得a=-0.143 1,b=0.832 8,代入式(5),式(6),可得序列X(0)′的预测模型为

(20)

进一步求得灰色均值模型预测序列为

(21)

3.2 基于傅里叶级数的残差一次修正

E={-0.049 1,-0.021 2,0.098 7,0.015 3,-0.037 9} .

(22)

取TF=5,kF=1,

CF=[0.002 3,0.036 4,-0.058 5].

(23)

将CF代入到式(7),可得残差修正序列为

EF={-0.067 7,-0.035 2,0.033 7,0.070 1,0.037 5} .

(24)

将序列EF(t)代入式(10),可得经傅里叶级数对残差进行一次修正后的预测序列为

(25)

3.3 建立马尔可夫预测模型

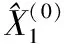
E={0,0.018 7,0.014 0,0.065 1,-0.054 8,-0.075 5} .

(26)

根据该序列的平均值μ和标准差σ将其划分为3个状态区间:[μ-1.3σ,μ-0.2σ]，[μ-0.2σ,μ+0.2σ]，[μ+0.2σ,μ+1.3σ],分别对应状态E1，E2，E3,其中,μ=-0.006 5，σ=0.057 6,具体3个状态区间为[-0.081 4 -0.018 0]，[-0.018 0 0.005 0]和[0.005 0 0.068 4],则残差序列状态见表5.