迭代直觉模糊K-modes算法

陈育丹，高翠芳，沈莞蔷，殷 萍

（江南大学理学院，江苏无锡 214122）

0 引言

在最近的几十年，数据科学家在挖掘真实生活数据方面面临着两大挑战：一方面，在现实生活中，只有少量的观测数据被标注出来；另一方面，由于资源和时间有限，给数据贴上标签也很昂贵。因此，无监督聚类技术在数据挖掘、模式识别、信息检索等分析应用中发挥着越来越重要的作用。数值型数据、分类型数据以及混合型数据是统计学中对数据的一般分类。目前关注数值型数据聚类的学者较多，研究成果较为丰硕，但是由于分类型数据的复杂特性，分类型数据聚类的相关研究还不够深入。首先，由于单个属性的领域缺乏固有的顺序，难以定义相似性概念，从而导致如何度量分类型数据对象之间的相似性成为一个难题。此外，对于数值型数据，类的原型往往由类的每个属性域中对象的均值组成，可以用来表示类。无论如何，计算分类型数据的平均值是不可行的，这意味着用于聚类数值数据的技术并不能直接适用于分类型数据，因此，对分类型数据聚类算法的研究具有重大意义。

许多文献报道了对分类型数据聚类算法的研究，其中在K-means 算法的基础上提出的KM（K-Modes）算法［1］及其模糊版本FKM（Fuzzy KM）算法［2］仍然是目前研究较为广泛的方法。而FKM 算法利用其具有概率隶属度值的模糊目标函数来处理聚类的重叠，具有优于传统的硬聚类方法的优点。FKM 算法被提出以后，Kim 等［3］提出了一种模糊质心算法，解决了FKM 算法质心表示信息缺失的问题。Bai 等［4］在目标函数中加入类间信息，改进了FKM 算法的目标函数，优化了算法的类间分离度。Saha 等［5］对每个类别属性使用权重因子，提出了一种加权的FKM 算法。白亮等［6］改进了FKM 算法中使用的0-1 度量，提出了一种基于对象对类隶属度相似性度量的FKM 算法——NDFKM（FKM based on New Dissimilarity）。为了避免初始类中心随机选择对聚类效果的影响，一些初始类中心选择算法相继被提出［7-10］。也有学者针对简单匹配相似性度量无法准确挖掘分类型数据的内在相关性，对分类型数据相似性度量展开了研究［11-14］。近年来，受到智能优化算法全局搜索能力极佳的启发，将智能优化算法与分类型数据聚类算法结合起来，提高其全局搜索能力亦吸引了许多学者的目光［15-18］。

虽然近年来分类型数据聚类算法已经取得了长足发展，但是相较于数值型数据聚类算法［19-23］，现有分类型数据聚类算法在处理聚类过程中的高模糊性以及不确定性等方面仍有欠缺。针对这个问题，Sarkar 等［24］用可信性测度衡量数据对象与类的隶属关系，提出了一种可信性K-modes 算法。Kuo 等［25］将加权FKM 算法与直觉模糊集融合，吸取了直觉模糊集处理不确定性问题的优势。Goyal 等［26］先将直觉模糊集融入到FKM 算法中，并在目标函数中加入直觉模糊熵最大化每一类中优良数据点，提出了一种直觉FKM（Intuitionistic FKM，IFKM）算法；然后将IFKM 算法与遗传算法的框架结合，扩大了最优搜索的范围。

然而IFKM 算法在度量数据对象之间的相似性时仅使用简单匹配相似性度量，未能充分挖掘同一类中数据对象的相似度以及属性特征对数据对象之间相似性的影响；并且，由于在迭代聚类的过程中仅把直觉模糊集作为判别数据类别的一种累加手段，没有将直觉模糊的思想贯穿于整个迭代过程，而是采用基于类属频率的方法确定新的类中心，IFKM 算法未能将直觉模糊在处理不确定性问题上的优势充分发挥。针对这两个问题，本文提出了一种迭代IFKM（Iterative IFKM，IIFKM）算法。

本文的主要工作有以下几点：

1）定义了一种加权的直觉模糊隶属度相似性度量；

2）提出了IIFKM 算法，该算法在聚类过程中将直觉模糊隶属度矩阵作为迭代信息贯穿于整个聚类过程，使得算法中的模糊思想得到充分体现。

1 FKM算法

FKM 算法［2］是通过搜索式（1）中目标函数的局部极小值对特征向量进行聚类：

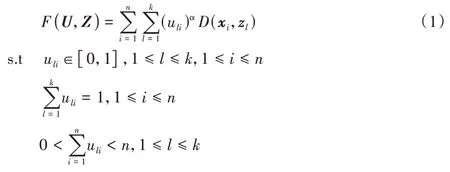
F的最小化是基于对U（隶属度矩阵）和Z的适当选择，采用式（2）～（3）进行隶属度以及类中心的迭代：

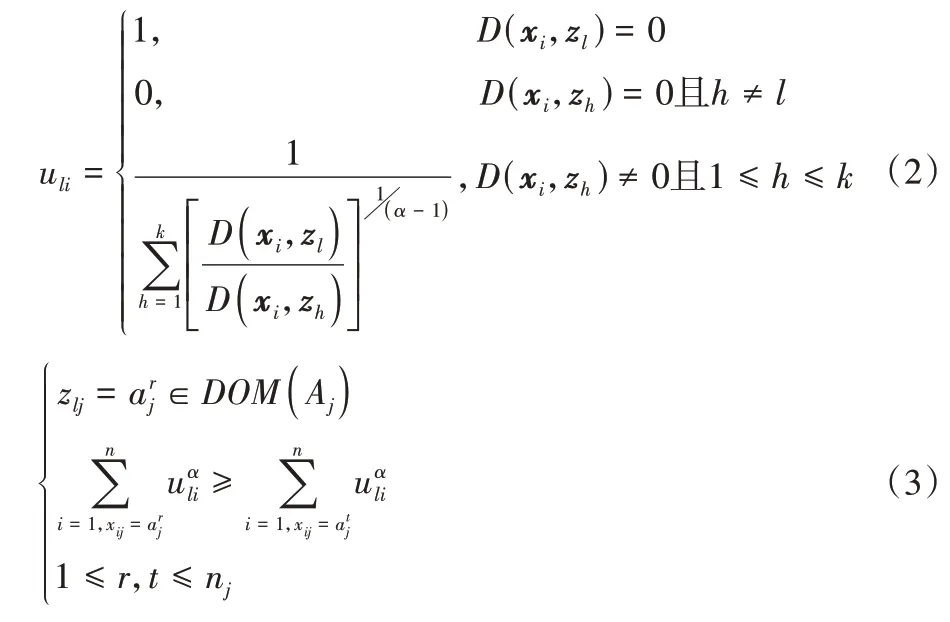
其中：uli为第i个数据xi=(xi1，xi2，…，xim)对第l个类的概率隶属度；α为模糊因子，一般来说α>1；zl=(zl1，zl2，…，zlm)为第l个Modes（类中心）。D(xi，zl)为第i个数据与第l个Mode之间的相异性度量，采用汉明距离度量对象之间的距离：

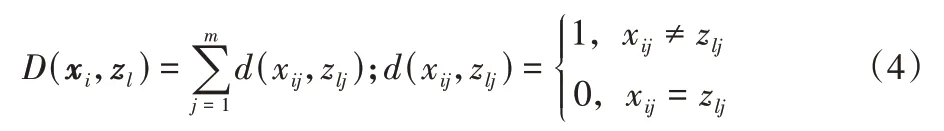
其中：nj为第j(1≤j≤m)维属性Aj的不同属性值的数目，为第j(1≤j≤m)维属性Aj的第t个属性值。

2 IFKM算法

文献［26］中提出的IFKM 算法旨在将直觉模糊集与直觉模糊熵融合到FKM 算法的框架中，以提高聚类性能。该算法首先将犹豫度加入到模糊隶属度中，得到直觉模糊隶属度值；然后在每一次迭代中根据直觉模糊隶属度判别数据对象所处类别，选择属性类别频率较高的数据对象作为新的集群中心，最后将直觉模糊熵加入目标函数中，最大化每一类优良数据点。

定义1设Y为一个论域，M是Y上的一个直觉模糊集（Intuitionistic Fuzzy Set，IFS），则M可表示为：

其中：Y是一个论域；uM(y)→[0，1]为直觉模糊集M的隶属函数；vM(y)→[0，1]为直觉模糊集M的非隶属函数，表示元素y对M的“支持程度”与“反对程度”，且对任意的y∈Y，都有0≤uM(y)+vM(y)≤1 成立。

进一步，称πM(y)=1-uM(y)-vM(y)为直觉模糊集M中元素y的犹豫度。显然，0≤πM(y)≤1，且如果πM(y)=0，则IFS 为模糊集；反之，如果πM(y)=1，则IFS 为完全直觉集。

直觉模糊补被用来构造IFS。建立直觉模糊补的常用方法有两种：Yager 生成函数和Sugeno 生成函数。根据Yager 的生成函数［27］，得到的IFS 为：

其中：β∈(0，∞)为非隶属度和犹豫度的控制参数。那么，犹豫度可以计算为：

考虑Sugeno 的生成函数［28］，IFS 和犹豫度可表示为：

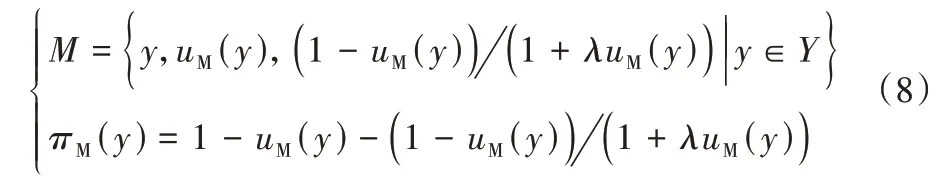
定义2设uM(y)、vM(y)、πM(y)为论域Y={y1，y2，…，yn}中元素的隶属度、非隶属度和犹豫度，M是Y上的一个直觉模糊集（IFS），则直觉模糊集M上的直觉模糊熵（Intuitionistic Fuzzy Entropy，IFE）定义为：

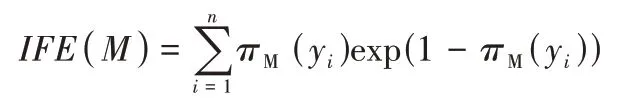
其中：πM(y)=1-uM(y)-vM(y)。

IFKM 算法源自直觉模糊集［29］。模糊集依赖于分级的隶属度值，直觉模糊集依赖于隶属度和非隶属度值，从而导致与域内每个元素相关联的犹豫值。在该算法中，犹豫值作为新参数在IFKM 算法的概念中加入了直观的隶属度。这个程度导致了一个对象在一个特定值的特定集群中的成员关系的不确定性。IFKM 算法的步骤如下：

步骤1 为k个集群分配初始集群中心或模式，令t=0。

步骤2 利用式（4）计算数据对象xi与类中心zl之间的距离矩阵D(t)。

步骤3 生成模糊划分矩阵或隶属度矩阵U(t)，如式（2）所示。

步骤4 利用式（9）计算犹豫度矩阵：

步骤5

1）计算直觉模糊隶属度矩阵U*(t)：

2）将xi分到第l个类如果。

步骤6 选择类别属性相对频率较高的xi作为新的代表，即集群中心或模式；

步骤7 重复步骤2）～6），直到|U*(t)-U*(t-1)|≤ε为止。

IFKM 算法的目标函数包含两项：1）常规直觉模糊集的改进目标函数；2）直觉模糊熵。可用公式表示为：

3 本文算法

本文所提IIFKM 算法使用FKM 算法的范式聚类分类数据。在本文算法中，将n个分类对象聚类成k个簇的目标是找到U和Z使目标函数F∗(U，Z)取得极小值。接下来本文将从相似性度量、类中心更新方式以及算法的具体步骤等方面详细论述本文所提IIFKM 算法。

3.1 加权的直觉模糊隶属度相似性度量

在分类型数据聚类算法中，相似性度量是一个特别重要的因素。一个好的相似性度量可以更好地刻画数据对象之间的相似程度，从而使得聚类算法取得更加理想的聚类效果。对于分类型数据聚类算法的相似性度量来说，简单匹配是一种常见的方法，许多分类型数据聚类算法都采用了简单匹配的思想［30-32］；然而，简单的匹配往往导致簇内相似性［33］较弱，忽略了分类值之间隐藏的相似性［34］。白亮等［6］基于对象对类的模糊隶属度提出了一种适用于FKM 算法的相似性度量，强化了类内相似性；但是相似性度量没有刻画聚类中不同属性的重要程度。本文以文献［6］中提出的相似性度量为原型，进一步考虑不同维度属性的贡献程度，并融合了直觉模糊隶属度定义了一种加权的直觉模糊隶属度相似性度量。

3.1.1 属性权重的计算

从信息论的角度来看，一个属性的重要性可以看作是数据集对该属性的不均匀程度。此外，在文献［35］中有描述，如果一个属性的信息含量高，那么该属性的数据集的不同质性也高。在文献［36］中，属性A的重要性通过它在每个属性值上的平均熵来量化，每个属性的权重可以如式（12）计算：

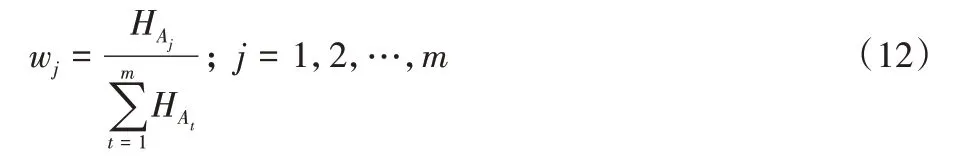
3.1.2 加权的直觉模糊隶属度相似性度量

定义3加权直觉模糊隶属度相似性度量：设对象集X={x1，x2，…，xn}，属性集A={A1，A2，…，Am}，类中心Z={z1，z2，…，zk}，xi∈X(1≤i≤n)，zl∈Z(1≤l≤k)。xi和zl分别被A描述为xi=(xi1，xi2，…，xim)和zl=(zl1，zl2，…，zlm)。本文定义的加权直觉模糊隶属度相似性度量（距离公式）为：

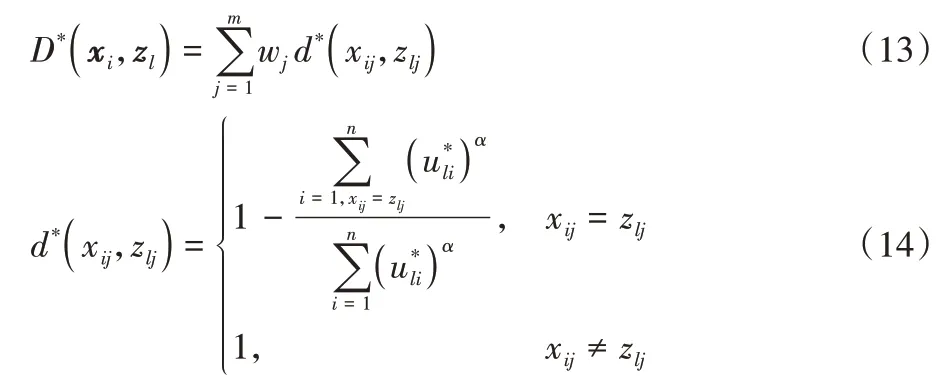
加权的直觉模糊隶属度相似性度量将数据对象对类的直觉模糊隶属程度以及属性权重作为衡量数据对象之间相似性的标准，强化了类内相似性与属性贡献度的同时，也与本文提出的IIFKM 算法更加契合。

3.2 隶属度及类中心更新规则

本文算法在构造直觉模糊集时并未如IFKM 算法一样选用Sugeno 的生成函数，而是采用了文献［27］中使用的Yager生成函数。故而本文算法的目标函数为：

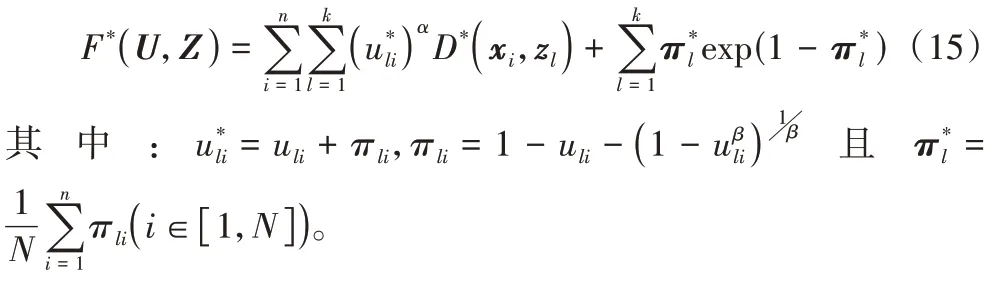
直觉模糊集构造方式的改变并未影响算法对数据对象隶属度的判断，故而本文算法的直觉模糊隶属度更新方式除犹豫度计算方法改为式（7）外，其他与IFKM 算法一致。

定理1IFKM 算法类中心更新规则：设对象集X={x1，x2，…，xn}，属性集A={A1，A2，…，Am}，DOM(Aj)=，其中nj为属性aj中不同属性值的数量(1≤j≤m)，类中心Z={z1，z2，…，zk}，xi∈X(1≤i≤n)，zl∈Z(1≤l≤k)。xi和zl分别被A描述为xi=(xi1，xi2，…，xim)和zl=(zl1，zl2，…，zlm)。则目标函数F*(U，Z)=取得最小值，当且仅当zlj=∈DOM(Aj)(1≤j≤m)，其中：

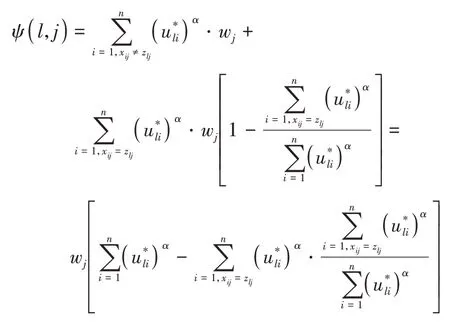
由于每个属性特征的权重wj以及每个数据对象对固定类的直觉模糊隶属度都是固定的，即固定，故当最大时ψ(i，j)取得最小值。

3.3 IIFKM算法的具体步骤

本文算法虽然融入了直觉模糊集与直觉模糊熵的思想并将其贯穿于整个迭代过程中，但是算法的思路与FKM 算法一样，都是通过迭代隶属度矩阵以及类中心来使目标函数达到极小值，故而算法的基本流程与FKM 算法并无太大区别。算法的具体步骤如下：

步骤1 随机选取数据集X中的k个样本作为初始类中心：Z(0)=(z1(0)，z2(0)，…，zk(0))。

步骤2 利用式（2）、（4）计算所有样本xi(1≤i≤n)对初始类中心Z(0)的初始隶属度矩阵U(1)；t=1。

步骤3 利用U(t)及式（7）计算数据集X中样本xi(1≤i≤n)对每个类中心的犹豫度πli(t)，从而根据式（10）得到直觉模糊隶属度矩阵U*(t)。

步骤4 根据式（16）计算k个新的类中心Z(t)=(z1(t)，z2(t)，…，zk(t))。

步骤5 根据新的类中心Z(t)更新加权的直觉模糊隶属度度量矩阵D*(t)，从而由D*(t)得到新的隶属度矩阵U(t+1)。

步骤6 重复步骤3）～5），直到|F*(t)-F*(t-1)|≤ε为止(1≤t≤T)，T为最大迭代次数。

4 实验与结果分析

4.1 实验数据集

本文从UCI 数据库中选取了Lung-cancer、Zoo、Dermatology、Breast-cancer、Mushroom 共5 个常用的真实数据集进行分析，其中，在Breast-cancer 和Lung-cancer 中对缺失属性值的样本进行删除。5 个数据集的简略描述如表1所示。

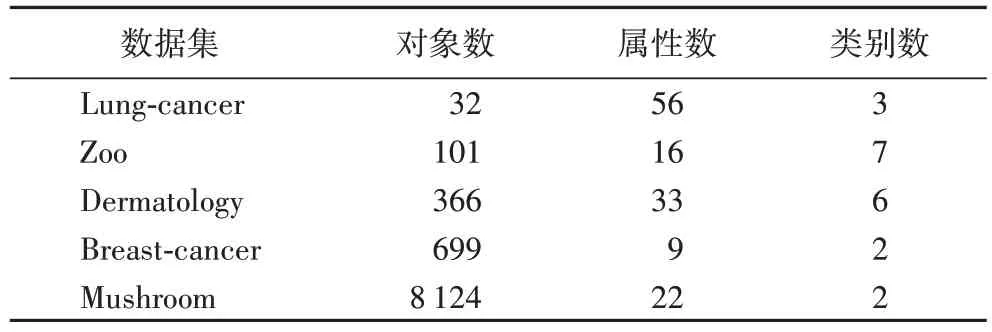
表1 数据集描述Tab.1 Description of datasets

4.2 聚类性能评估指标

本文选取了3 个常用的聚类性能评估指标来分析算法的聚类质量：分类正确率AC（accuracy）、分类精度PR（precision）和召回率RE（recall）［37］。这三个指标是利用真实类标签来评价每个给定数据集的聚类结果的外部标准，AC是对聚类整体正确率的评价；PR是精确性的度量，表示被分为正例的示例中实际为正例的比例；RE是覆盖面的度量，度量有多少个正例被分为正例。如果聚类结果接近真实的类分布，则这些评价指标的值是高的。AC、PR、RE的定义如下：

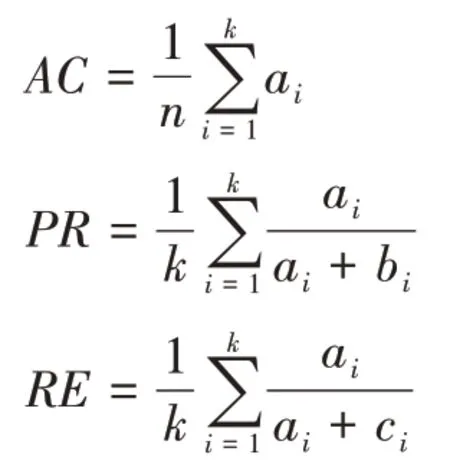
其中：ai是正确分配给类Ci的数据对象的数量；bi表示错误地分配给类Ci的数据对象的数量；ci为类Ci错误拒绝的数据对象的数量；n为整个数据集中全部数据对象的数量；k为数据集中包含的类的数量。

4.3 非隶属度和犹豫度的控制参数调试

对于直觉模糊聚类算法，需要适当设置非隶属度和犹豫度的控制参数。在数值型数据的直觉模糊C均值算法中，Chaira［20］将非隶属度和犹豫度的控制参数设置为0.85。文献［26］中的分类型数据IFKM 算法的犹豫度控制参数λ设置为2。但是由于本文算法的直觉模糊集构造与文献［26］不一致，犹豫度的计算方式也不同，所以本文算法的犹豫度控制参数需要重新调试。经过实验分析，本文提出的分类型数据的加权直觉模糊聚类算法在β=0.85 时表现不佳，且当β>2.5 时，聚类效果亦不理想；进一步，与文献［20］中β<0.5 时聚类效果失真类似，本文算法在β<0.8 时，出现类中心重合的现象。故在接下来的实验分析中，将模糊因子α设置为1.1［2］，且分别取β为0.85、0.95、1.05、1.85、2.0、2.5 验证本文算法的性能。这里将IIFKM 对各数据集分别执行100次并求出AC、PR、RE的均值记录至表2 中。从表2 可看出，IIFKM 算法的聚类效果受犹豫度的控制参数β影响，在本文的5 个数据集中，Lung-cancer、Zoo 和Breast-cancer 数据集的β取值为0.95 时聚类效果最优，Dermatology 和Mushroom 数据集的β取值为2.0 聚类效果最优。

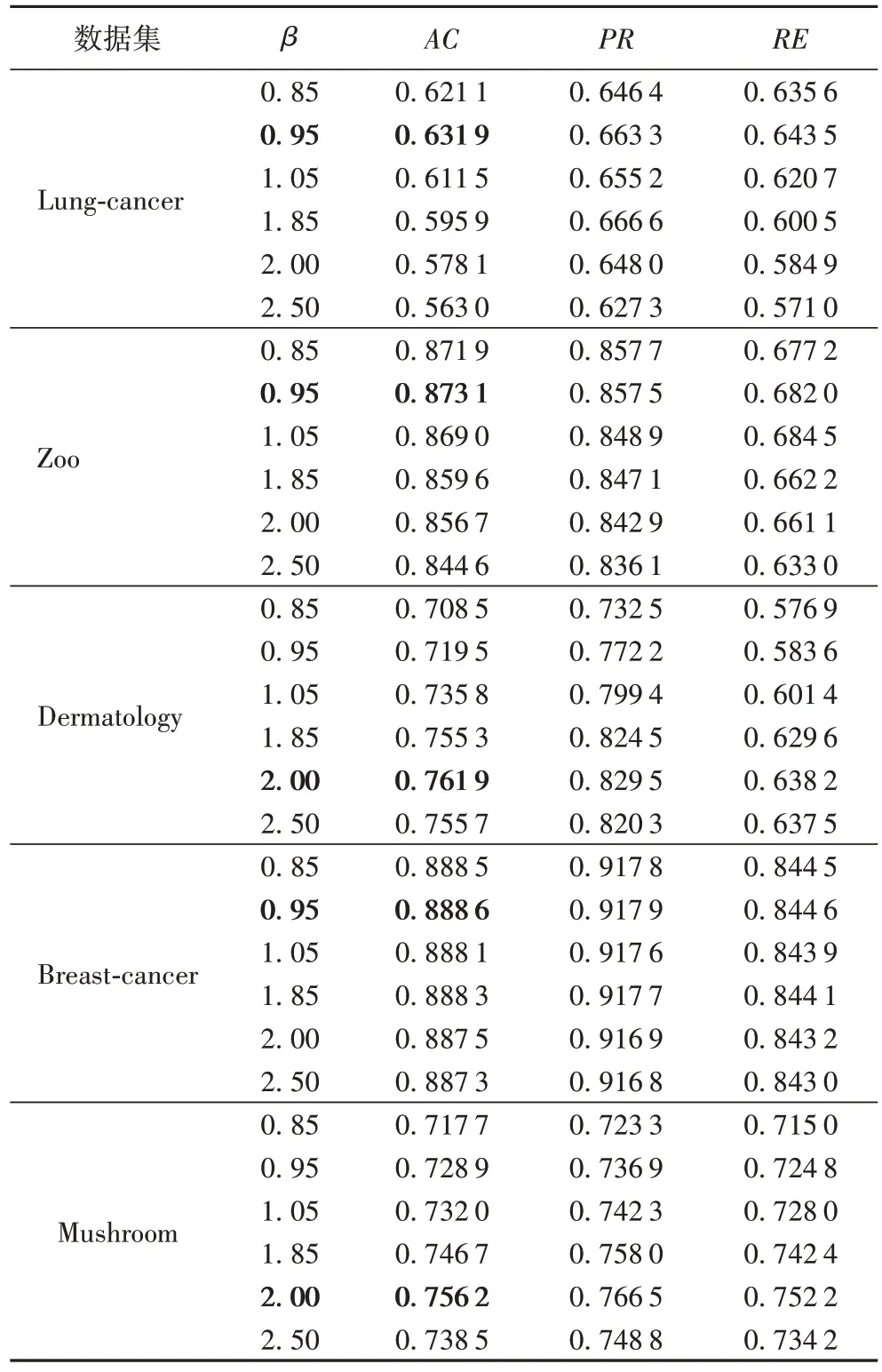
表2 IIFKM算法在不同β值时的AC、PR、RETab.2 AC，PR，RE of IIFKM algorithm with different values of β

4.4 聚类性能分析

各算法通过Matlab2018a 编程运行，对KM［1］、FKM［2］、IFKM［26］、NDFKM［6］和本文IIFKM 算法进行分析，求出聚类性能指标AC、PR和RE。算法参数设置为：FKM 和IIFKM 的阈值ε参照文献［24］以及具体实验设置为0.000 01，同时将最大迭代次数T设置为100，算法的模糊因子α按文献［2］推荐的设置为1.1，非隶属度和犹豫度的控制参数β，从表2 所示的实验结果可知，β=0.95，2.0 时本文算法取得较好聚类结果。为了使聚类结果最优，Lung-cancer、Zoo 和Breast-cancer数据集的β取值0.95，Dermatology 和Mushroom 数据集的β取值2.0。由于上述五种算法均受初始类中心的影响较大，每次运行的结果都可能因其初始类中心的不同而有差异。为了避免随机性，在5 个数据集上，各算法分别运行100 次后，再比较最终结果的平均值。

从表3 可以看出，IIFKM 算法的聚类效果在整体上是优于其他4 种算法的。除了Zoo 数据集，IIFKM 算法在Lungcancer、Dermatology、Breast-cancer 数据集上均表现良好。在AC和RE这两个指标上，相较于IFKM 算法，有7%～11%的提高；相较于NDFKM 算法，也有2%～6% 的提高。这说明IIFKM 算法在正确聚类和聚类查准上表现优异。并且除了在Zoo 数据集上，IIFKM 算法的PR值略低于IFKM 算法外，在其他数据集中IIFKM 算法的PR值均有一定提升，说明算法在每一类中的查准能力也是有保证的。此外由图1 可以看出，本文算法的准确聚类能力是稳定的，除了在Zoo 数据集上聚类的稳定性略差于其他算法，在其他4 个数据集中的稳定性均优于其他算法，尤其是在Dermatology 数据集中，在表现出优秀的稳定性的同时聚类准确率及其上限均高于KM、FKM、IFKM 和NDFKM 算法。

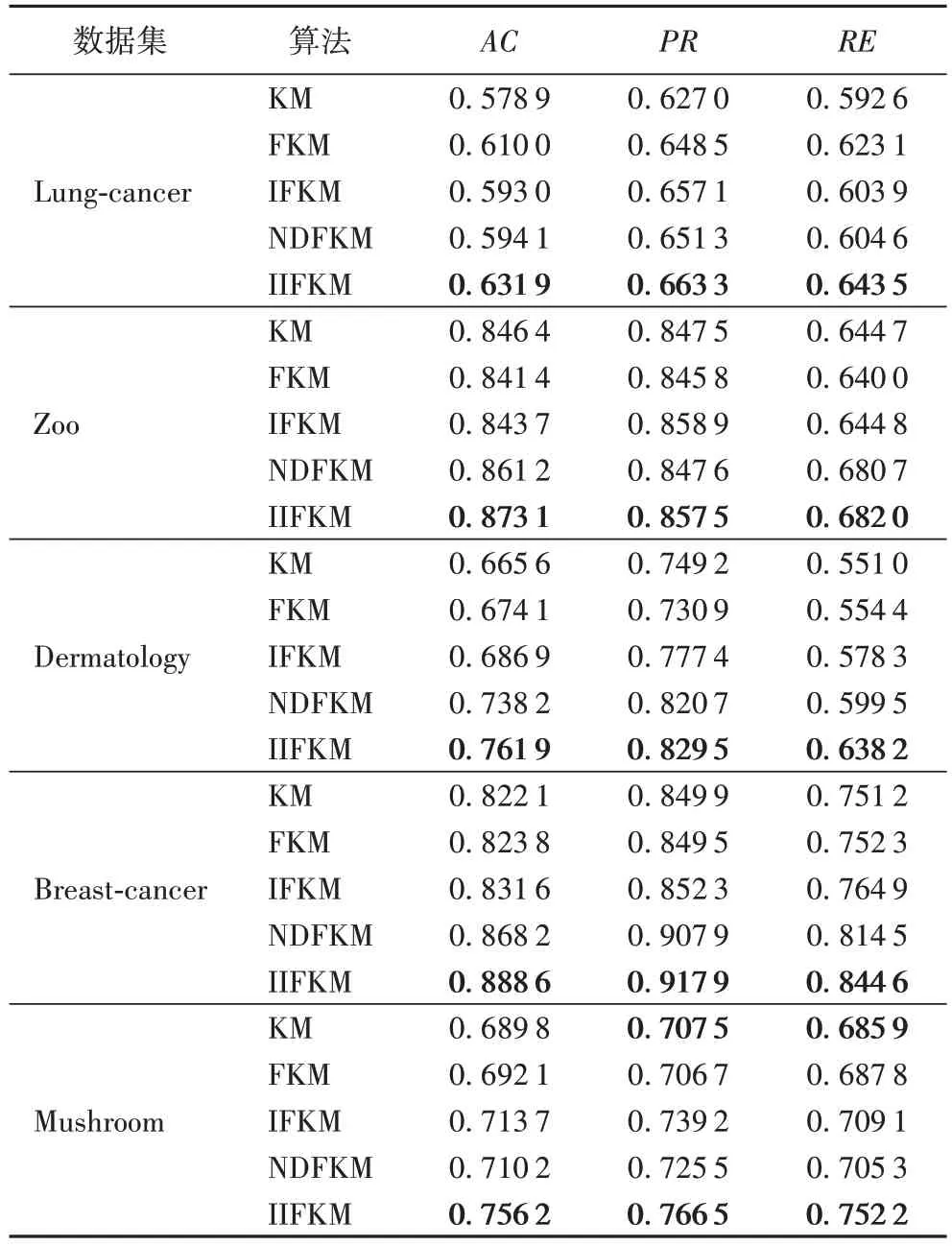
表3 五种算法的实验结果Tab.3 Experimental results of five algorithms

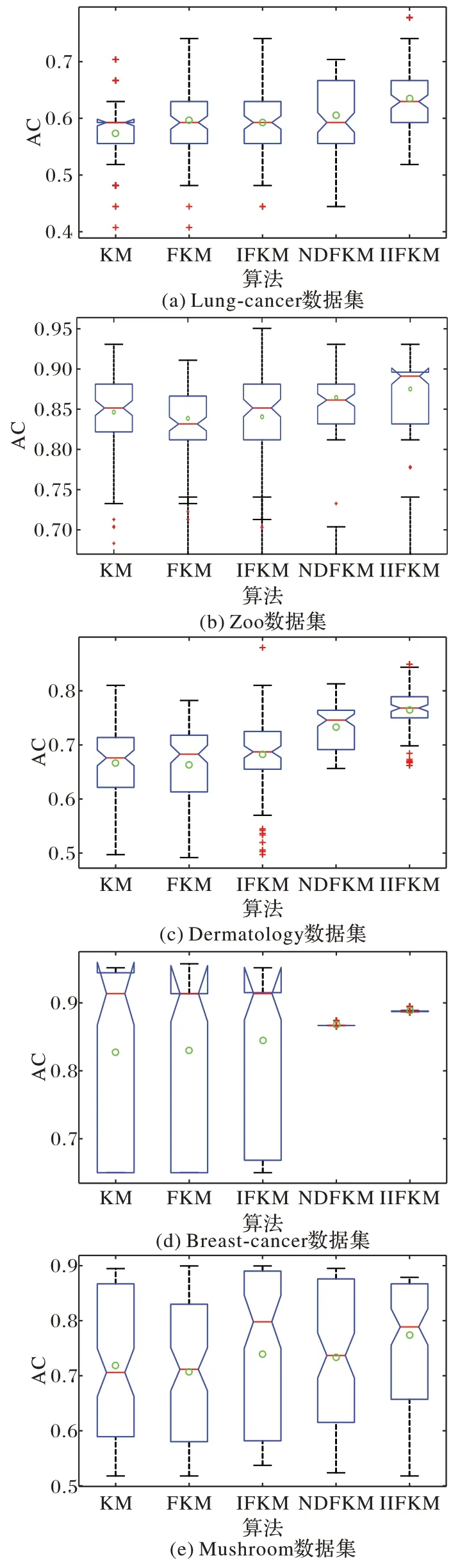
图1 各算法在5个数据集上的AC箱型图Fig.1 AC box plots of each algorithms on 5 datasets

为了进一步验证本文提出的IIFKM 算法框架的有效性，将本文算法中相似性度量换成和IFKM 算法中一样的简单匹配相似性度量，在Matlab2018a 中与IFKM 算法作对比实验后将实验结果记录于表4。为了避免随机性，在实验过程中，在每个数据集上对算法执行100 次后取平均聚类结果。从表4 所示的实验结果可知，本文所提IIFKM 算法框架在简单匹配相似性度量（IIFKM0）下，比IFKM 算法的聚类效果更好。这表明本文算法将直觉模糊隶属度作为聚类过程的迭代信息是正确、有效的。

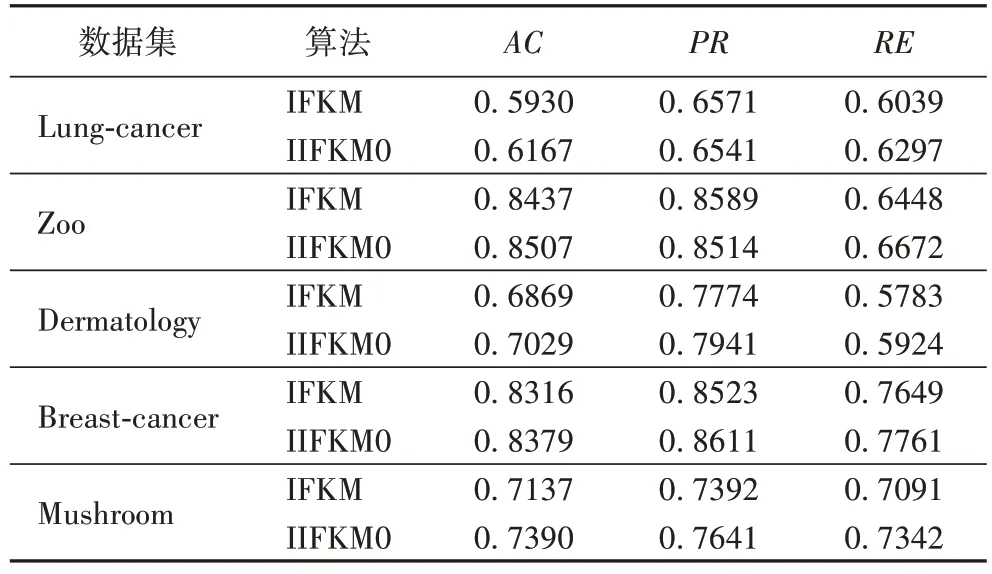
表4 IFKM算法和IIFKM0算法的实验结果对比Tab.4 Comparison of experimental results of IFKM algorithm and IIFKM0 algorithm

5 结语

本文算法将直觉模糊隶属度矩阵作为迭代信息贯穿于整个聚类中，充分发挥了直觉模糊集在聚类过程中处理不确定性问题的优势。由于IFKM 算法在度量相似性时采用汉明距离，不足以清晰度量对象之间的相似程度，本文定义了一种加权的基于对象对类的直觉模糊隶属度相似性度量。通过与K-modes、FKM 以及IFKM 等算法的实验对比，实验结果表明本文算法在聚类准确率、类纯度以及召回率等方面均有提升。不过，由于本文算法的初始类中心是随机选取的，如果初始类中心选取了离群点，算法效果比较糟糕，后续可加入优质初始类中心选择算法进一步提升算法性能；并且，本文虽然对犹豫度控制参数β进行了初步调试，但是如何给出一个比较明确的参数选择指南，本文还未有定论，后续会对此进行进一步研究。