中国数学文化融入课堂教学各环节的尝试

文/ 广州市番禺区石北中学 麦秀銮

在新的一轮课程改革中，人文知识越来越多地融入高中数学课程，在《普通高中数学课程标准》中强调，高中数学课程要注重数学文化等人文知识的渗透。教师在教学各环节融入文化知识，有意识地引导学生在学习中感悟数学的文化价值和审美价值，引领学生形成正确的人生观、价值观。下面是笔者尝试把中国数学文化融入教学各环节中的教学片段，供大家参考。

一、利用中国数学文化激发学生学习新知识的兴趣

在人教A 版必修5《数列的概念与简单表示》中，教材利用古希腊毕达哥拉斯学派研究的三角形数、正方形数作为一个例子，引出和归纳“数列”这个全新知识的概念，明显，教材的目的是为了突显数列中每一项和项数的关系。在教学过程中，笔者尝试利用学生熟悉的、与数学相关的人文知识引进数列的概念，让学生在学习过程充满熟悉感，感受到数学与生活的息息相关。

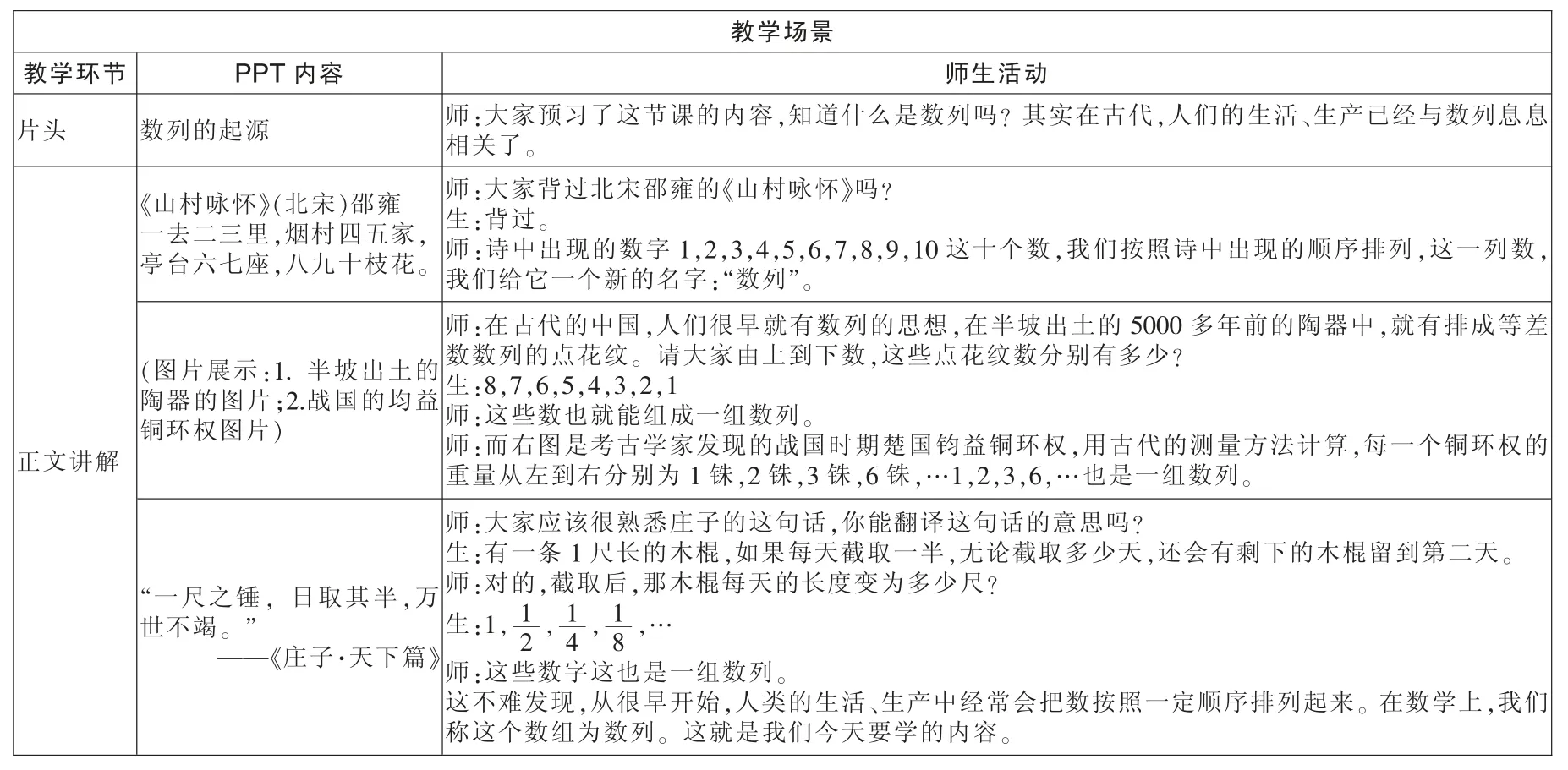
教学场景教学环节片头PPT 内容数列的起源《山村咏怀》（北宋）邵雍一去二三里，烟村四五家，亭台六七座，八九十枝花。师生活动师：大家预习了这节课的内容，知道什么是数列吗？ 其实在古代，人们的生活、生产已经与数列息息相关了。师：大家背过北宋邵雍的《山村咏怀》吗？生：背过。师：诗中出现的数字 1，2，3，4，5，6，7，8，9，10 这十个数，我们按照诗中出现的顺序排列，这一列数，我们给它一个新的名字：“数列”。正文讲解（图片展示：1. 半坡出土的陶器的图片；2.战国的均益铜环权图片）师：在古代的中国，人们很早就有数列的思想，在半坡出土的5000 多年前的陶器中，就有排成等差数数列的点花纹。 请大家由上到下数，这些点花纹数分别有多少？生：8，7，6，5，4，3，2，1师：这些数也就能组成一组数列。师：而右图是考古学家发现的战国时期楚国钧益铜环权，用古代的测量方法计算，每一个铜环权的重量从左到右分别为 1 铢，2 铢，3 铢，6 铢，…1，2，3，6，…也是一组数列。“一尺之锤， 日取其半，万世不竭。 ”——《庄子·天下篇》师：大家应该很熟悉庄子的这句话，你能翻译这句话的意思吗？生：有一条1 尺长的木棍，如果每天截取一半，无论截取多少天，还会有剩下的木棍留到第二天。师：对的，截取后，那木棍每天的长度变为多少尺？生：1， 1 2 ， 1 4 ， 1 8 ，…师：这些数字这也是一组数列。这不难发现，从很早开始，人类的生活、生产中经常会把数按照一定顺序排列起来。 在数学上，我们称这个数组为数列。 这就是我们今天要学的内容。

二、 利用中国数学文化突破学习难点

学生在学习人教版必修三的《球的体积和表面积》中，教材的正文并没有让学生了解球体积公式的推导过程，而是直接让学生记下这个公式，只是在本章节的最后，以阅读“探究与发现”的形式让学生初步了解祖暅原理推导球体体积公式的原理。在教学过程中，笔者尝试让学生通过了解球体体积公式推导的发展过程，揭示球体体积公式的本质，突破教学难点，完成教学目标。

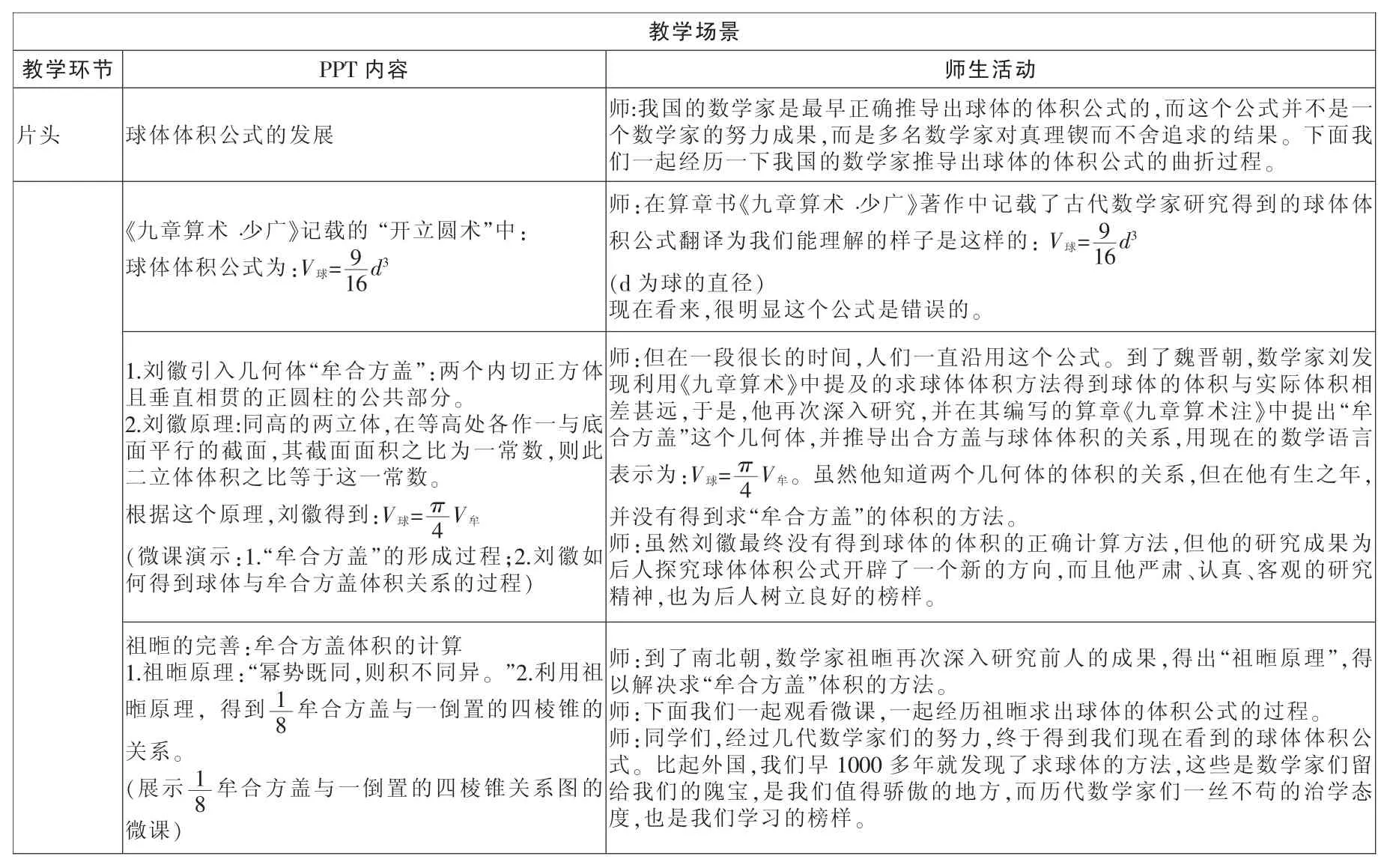
教学场景教学环节PPT 内容片头 球体体积公式的发展《九章算术·少广》记载的 “开立圆术”中：球体体积公式为：V球= 9 16d3师生活动师:我国的数学家是最早正确推导出球体的体积公式的，而这个公式并不是一个数学家的努力成果，而是多名数学家对真理锲而不舍追求的结果。 下面我们一起经历一下我国的数学家推导出球体的体积公式的曲折过程。师：在算章书《九章算术·少广》著作中记载了古代数学家研究得到的球体体积公式翻译为我们能理解的样子是这样的： V球= 9 16d3（d 为球的直径）现在看来，很明显这个公式是错误的。1.刘徽引入几何体“牟合方盖”：两个内切正方体且垂直相贯的正圆柱的公共部分。2.刘徽原理:同高的两立体，在等高处各作一与底面平行的截面，其截面面积之比为一常数，则此二立体体积之比等于这一常数。根据这个原理，刘徽得到：V球=π师：但在一段很长的时间，人们一直沿用这个公式。 到了魏晋朝，数学家刘发现利用《九章算术》中提及的求球体体积方法得到球体的体积与实际体积相差甚远，于是，他再次深入研究，并在其编写的算章《九章算术注》中提出“牟合方盖”这个几何体，并推导出合方盖与球体体积的关系，用现在的数学语言表示为：V球= π 4 V牟（微课演示：1.“牟合方盖”的形成过程；2.刘徽如何得到球体与牟合方盖体积关系的过程）4 V牟。 虽然他知道两个几何体的体积的关系，但在他有生之年，并没有得到求“牟合方盖”的体积的方法。师：虽然刘徽最终没有得到球体的体积的正确计算方法，但他的研究成果为后人探究球体体积公式开辟了一个新的方向，而且他严肃、认真、客观的研究精神，也为后人树立良好的榜样。祖暅的完善：牟合方盖体积的计算1.祖暅原理：“幂势既同，则积不同异。 ”2.利用祖暅原理， 得到 1 8 牟合方盖与一倒置的四棱锥的关系。（展示 1 8 牟合方盖与一倒置的四棱锥关系图的微课）师：到了南北朝，数学家祖暅再次深入研究前人的成果，得出“祖暅原理”，得以解决求“牟合方盖”体积的方法。师：下面我们一起观看微课，一起经历祖暅求出球体的体积公式的过程。师：同学们，经过几代数学家们的努力，终于得到我们现在看到的球体体积公式。 比起外国，我们早1000 多年就发现了求球体的方法，这些是数学家们留给我们的隗宝，是我们值得骄傲的地方，而历代数学家们一丝不苟的治学态度，也是我们学习的榜样。

整节课下来，学生在充满数学文化的课堂里进行思维的提升。学生在学习科学知识的同时体会到数学家刘徽和祖暅在球体的体积公式推导过程中刻苦钻研的作风，对真理锲而不舍的追求精神。学生在蕴含着大量优秀中国数学文化的课堂里学习新知识，学生不但感受到这些数学文化所蕴含的精神，也激发学生学习的内在动力，增强学生克服困难的信心。