城域级视频智能卡口规划布局方法

2022-02-28程峰潘飞刘纯陈潇湖北省武汉市公安局

警察技术 2022年1期

程峰潘飞刘纯陈潇湖北省武汉市公安局

一、视频卡口规划关键问题

经过多年建设，各地视频卡口基础设施不断完善，但是，当前仍然面临两个方面的问题。一是建多少，二是建在哪（或如何优化、如何更新升级）。传统的“圈、块、格、点”布局思路虽然给出了定性的原则，但经验、主观性较强，无法定量给出答案。

不同于文献[1]所述的过程覆盖方法，本文所述规划布局的目标是在最大限度消除侦查对象轨迹不确定性的前提下，最小化视频卡口的部署数量。鉴于轨迹不确定性主要来源于道路分叉，本文以道路分叉口作为基本节点，以路网为基础分析网络。侦查对象每次被智能卡口捕获，其轨迹不确定性即被消除，故已部署智能卡口的节点可视为路网上的陷阱节点。在含有陷阱节点的网络上，从任意一点出发，首次抵达任一陷阱节点的时间期望称为平均首达时间（MFPT）[2]，为便于理解，本文中后续部分统称为平均捕获时间。显然，网络中的陷阱节点越多，侦查目标不确定性越小。同时，陷阱节点布局越合理（处于对象大概率经过的路径上），平均捕获时间也越小。因此本文以平均捕获时间作为点位布局的主要评价指标。

综上所述，规划布局可抽象为如下目标优化问题，即：

给定网络平均捕获时间，求点位规划，使得网络布点总数最少。或者给定点位总数量，求点位规划，使得网络平均捕获时间最小。

由于上述两个问题互为对偶问题，本文下述部分将着重阐述问题1的求解方法。

具体来说，以道路分叉点为候选部署节点，记为ci，二元决策变量xi表示候选节点是否被选中为卡口部署点，即陷阱节点。当候选节点被选中为卡口部署点时，xi=1，否则xi= 0。以Tmfpt表示网络平均捕获时间，Tc表示网络平均捕获时间的设计目标值，则优化目标函数为：

求解上述问题，需明确网络的基本性质以及侦查对象的普遍动力学规律。为此，本文接下来内容组织如下：第2章分析视频侦查视角下城市路网的基本性质，揭示其高度的非均匀性，具备对其进行“切块分格”的基础条件；第3章证明了在复杂城域级路网条件下，无偏随机游走与Levy flight模型具有相似性，具备对一般运动目标的普适描述能力，并以无偏随机游走作为本文的目标运动动力学模型；第4章以马尔可夫无偏随机游走步数为尺度，对不同尺度网络社团进行分割，并以稳定性为条件，给出优选稳定分割的方法；第5章在前述基础上，基于网络多陷阱吸收模型，提出具体关键节点的定位思路及具体求解方法；第6章以某市为例，进行布点规划，并通过模拟计算实验验证了前述模型、算法的可行性和有效性。

二、视频侦查视角下的路网性质

文献[3]指出波士顿公交网络存在小世界特性，文献[4]对城市路网进行分析，指出其具备小世界特性，在此基础上，文献[5-7]分别研究了国内部分城市的路网结构。但是均是以道路本身作为路网的基本结构单元，以道路之间的关联关系为边，与本文研究方向不符。因此，本文以导致目标轨迹发散的道路交叉口为网络节点，以交叉口之间的道路连接为边，构建路网拓扑结构。文献[8]中指出，现已成型的城市道路体系可归纳为四种形式，分别是方格网式、自由式、环形放射式和混合式，其中又以方格网式最为常见。整体来看，网络接近于规则网络。图1为某市路网图，其中左图为路网拓扑，可以看到整体具备明显的规则网络结构，右图为网络节点度分布图，具备高斯分布的特性，网络节点的平均度为2.84，大量节点的度为2~4之间，即常见的路口拐弯处、丁字路口和十字路口。

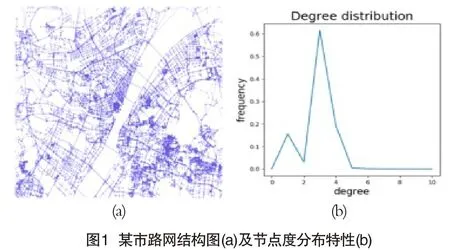
对于规则网络，节点分布均匀，网络聚类系数低，平均最短路径长度大。图1所示的某市路网，具备显著的规则网络特性，聚类系数为0.06，网络直径为175，平均路径长度为46.6，内部连接稠密、边界连接稀疏的网络社团结构特征整体不明显。

但同时应注意到，侦查目标一旦搭乘巴士、地铁等公共交通工具，会发生目标直接从起点，在不被任何卡口捕获的条件下，直接出现在另一任意站点的现象。从而导致在路网中本无关联的节点对成为邻居节点，直接改变原网络中的网络邻接和距离关系。

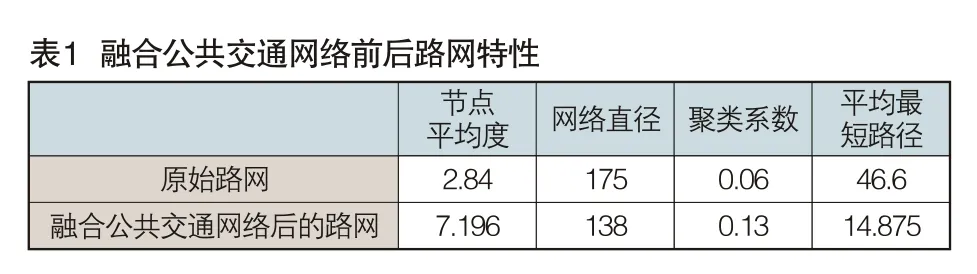
因此，本文将公共交通数据以space P方法[9]加入路网中，形成视频侦查视角下的路网拓扑结构。由于公共交通网络本身具备小世界特性，加入路网后，等价于为规则网络增加了长程链接，根据文献[10]，合并后的路网将具备小世界特性。图2所示为合并后的路网及其节点度分布，可以观察到幂律分布特性。融合前后网络关键指标对比如表1所示，与之前相比，网络聚类系数明显提升，平均路径长度显著减小，具备形成网络社团并进而对其网络进行分格切块的基础。

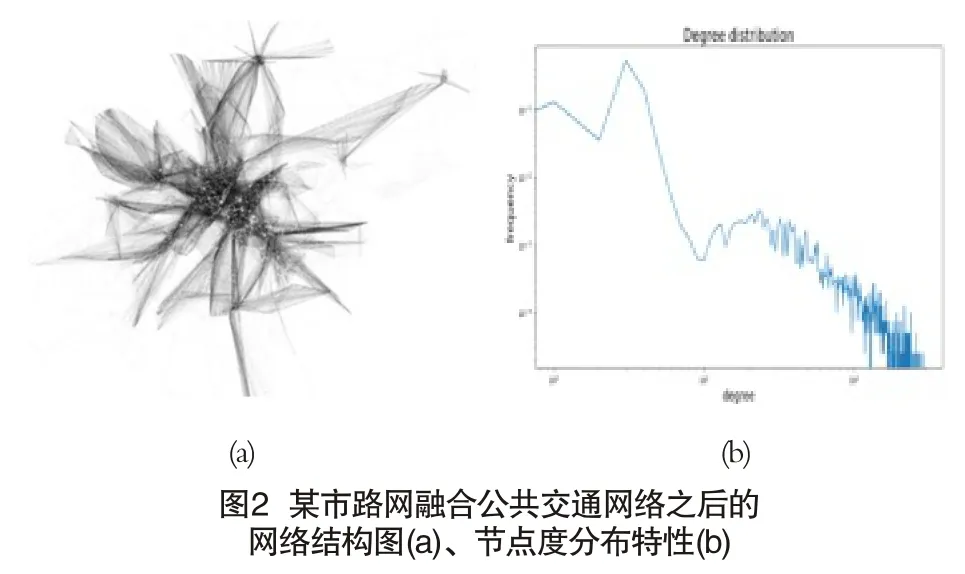
三、复杂路网中的目标运动模型

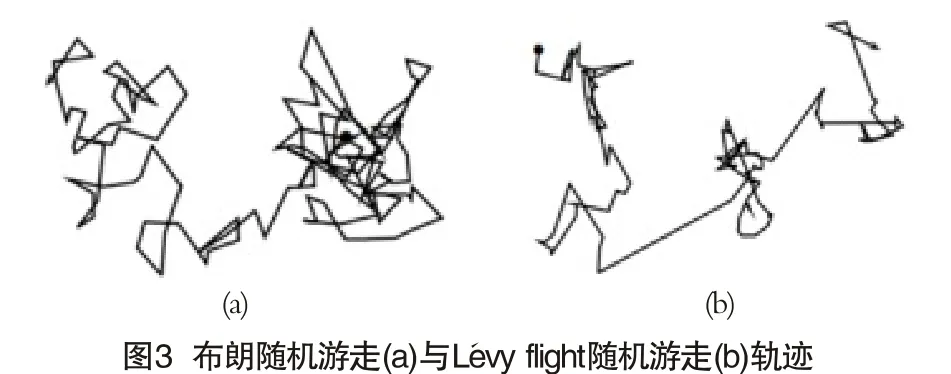
无偏随机游走是在任意维度的空间中，一个点随机地向任意方向前进任意长度的矩离，然后反复这个过程。Levy flight是随机游走的一种，它的每一步方向完全随机而各向同性，但步长的分布是重尾分布。近年来，有相当多的研究表明很多动物的移动模式可以用Levy flight来描述，甚至人类的移动模式也和Levy flight高度吻合[11,12]。图3所示为布朗随机游走与Levy flight随机游走的轨迹[13]，其中Levy flight随机游走表现为目标在一个局域范围内进行反复徘徊后，往往伴随一个长距离的跳跃，然后再度进入一个局域范围内的徘徊，与平时侦查工作经验基本一致。

由文中第2章路网构造方式可知，在每一步随机游走过程中，下一步跳跃步长为s的概率与节点本身的度密切相关。当节点的度为1~4之间时，为网络的普通路口节点，只可能游走到下一个路口，不存在远距离跳跃的情况。当节点的度较大时，节点为车站等中枢节点，可以在站点之间进行远距离跳跃。根据城市交通一般规划，站点呈线性或者环形、网状分布。给定站点数量，在线性分布条件下，跳跃距离最远，网状分布条件下，跳跃距离最近。则复杂路网上无偏随机游走下一步行走步长为s的概率满足：

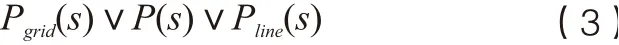
其中，

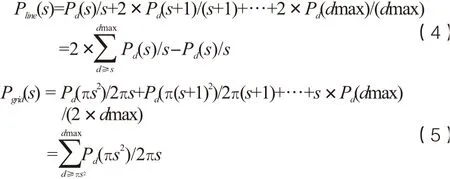
Pd为网络节点的度分布概率。由第2章可知，网络节点度满足幂律分布，即：

式（4）、（5）均为p级数，无法求取显式表达式，但是根据式（3）、（4）、（6）可知：

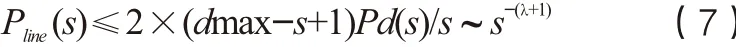
根据式（3）、（5）、（6）可知：

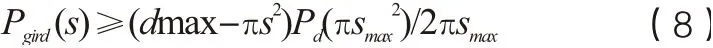
因此，根据式（3）、（7）、（8），有：

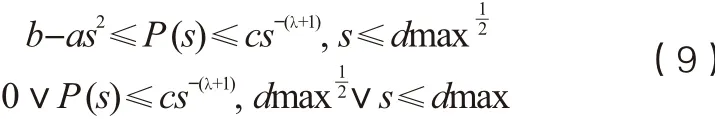
由此可知P(s)具备重尾分布特征，复杂路网上的无偏随机游走具备Levy flight类似的特性。图4(a)所示为某市复杂路网上无偏随机游走轨迹，可以看到轨迹具备明显的Levy flight轨迹特征，图4(b)、(c)分别为在该网络上随机游走1000次、每次5000步的步长分布，最长单次跳跃步长超过21km，图4(b)显示步长分布具备重尾特性，更进一步，图4(c)显示，对数坐标系下，步长分布呈负斜率直线分布，具备幂律特性。因此，本文在复杂路网上采用无偏随机游走作为侦查对象的一般运动学模型。

四、无偏随机游走视角下多尺度社团分割

网络社团是指由网络节点所构成的团块组织，其内部节点之间连接致密，内部节点与外部节点连接稀疏，因此，其社团边界节点天然成为区域封控的关键节点。当前，已经有大量的研究聚焦于如何发现网络社团及其层级结构，主要是应用图的组合属性，包括平衡切割、归一化切割、模块度及其各种拓展和优化算法[14,15]，但是此类方法关注的是图本身的拓扑性质，在社团尺度选择上与侦查业务无明确关联。

文献[16]指出，复杂网络上的马尔可夫随机游走过程提供了一种在各种尺度上动态揭示网络社团结构的机制，随机游走的时间尺度（对于离散时间系统，时间尺度即对应游走步数）即对应了社团分割过程的分辨率。直观理解即是在马尔可夫游走条件下，侦查对象以更大的概率在社团内部徘徊，更小的概率进行跨社团转移。侦查对象随机游走的步数即对应了不同分辨率下的社团结构，也就是“圈、块、格”逐层嵌套的层级结构。

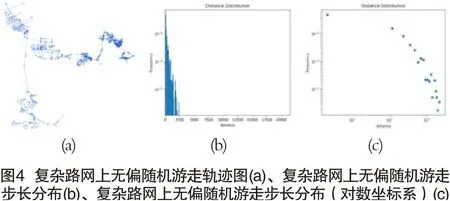
对于网络上的无偏随机游走过程，记A为网络邻接矩阵，M为随机游走的状态转移矩阵，d为各节点度组成的列向量，矩阵H为网络的社团分割矩阵，对于H的每一个元素，若节点i划归为社团j，则Hij= 1，否则，Hij=0，那么在时刻t的聚类自协方差矩阵为：

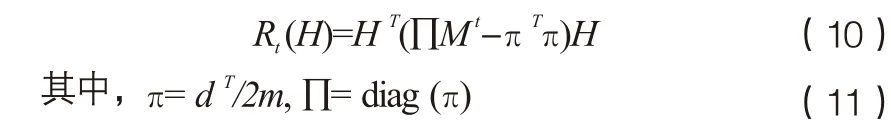
定义社团划分H的马尔可夫稳定性为：

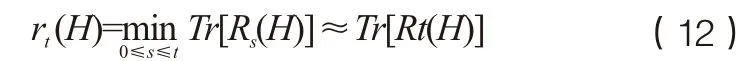
式（12）反映了经过t步随机游走之后，目标仍然留在社团内的概率大小，因此网络社团划分问题转化为求解使式（12）最大化的矩阵H，即：

上述优化为NP-hard问题，无法直接求解，因此需转而寻求其他启发式优化方法。根据式（10）、（12）、（13）可知：

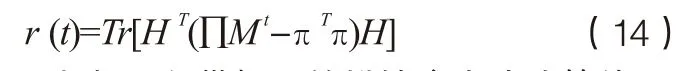
注意到式（14）与无向带权图的模块度表达式等价，对应的等价无向带权图的邻接矩阵为：

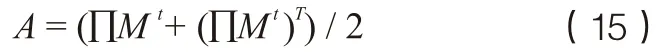
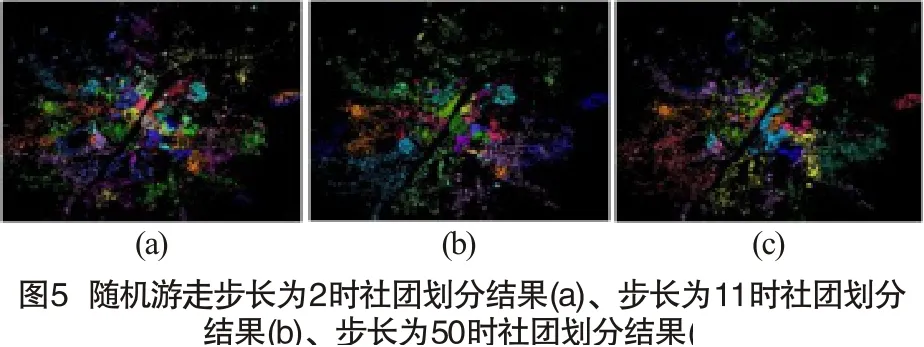
故对时刻为t的离散随机游走条件下的网络社团划分，可以等价为邻接矩阵为式（15）所述无向带权图的社团网络划分，划分依据为等价图的模块度。本文采用Louvain算法[17]分别在1~50步随机游走条件下对复杂路网进行社团划分，结果如图5所示。可以看到，不同的随机游走尺度对应了不同的社团分割分辨率，更大的随机游走步数对应了更大的社团结构。

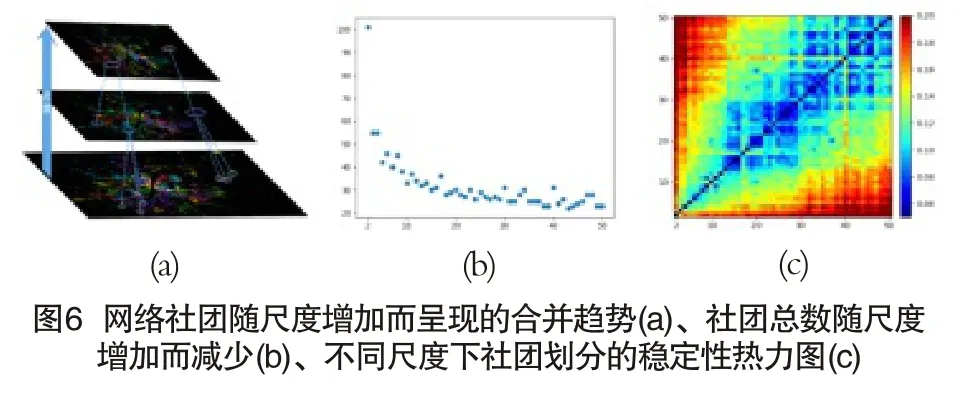
站在建设规划的角度，将所有分辨尺度全部实现是一种理想极端情况，实际规划中难以实现，同时也失去了切块分格的意义。在尺度的选择上，一个好的网络分割应该在不同的分割尺度上具有较好的稳定性，即应挑选出随着随机游走步长变化，分割结果相对平稳的方案。图5（a）所示为随尺度变化，网络社团划分的嵌套结构，整体上，随着观察尺度的增大，网络社团呈现合并的趋势。图5（b）所示为2~50步随机游走尺度下分别进行社团分割所得的网络社团数量，可以看到社团划分的数量整体随尺度的增加而减少。为度量网络社团划分的稳定性，引入网络分割的归一化信息差异指标[18]：

其中，P1、P2为两种不同的网络分割，H(P1|P2)表示给定分割P2条件下，选定分割P1的条件熵。V(P1,P2)取值在0到1之间，反映了两种网络分割的差异度，V的值越大，则两种分割的差异性越大。图6（c）所示为对2~50步随机游走尺度分别进行社团分割，并对分割稳定性进行计算所得结果。可以看到在27、35、43步等尺度上，分别出现相对稳定区域。这些相对稳定的、不同尺度的社团结构即构成了逐层嵌套的封圈、切块、分格基本布局框架。

五、基于平均捕获时间的定点模型

根据前文构建的复杂路网模型和目标运动模型，式（1）（2）所描述的布点计算问题可进一步进行求解。

记A为网络邻接矩阵，Z为前文所述复杂路网的对角度矩阵，即：

记I为N×N阶单位矩阵，则网络的归一化拉普拉斯矩阵表示为：

记Г为网络中卡口（即陷阱）节点的集合，根据文献[19]易知，从非卡口节点出发，以无偏随机游走方式，首次到达任意卡口节点的时间T'可表示为：

其中，L'为归一化拉普拉斯矩阵去掉卡口节点对应的行与列之后剩余的子矩阵，e为N-|Γ|维单位向量。

则从网络任意一点出发，经过无偏随机游走，直至被网络卡口节点首次捕获的平均时间（步数）表示为：

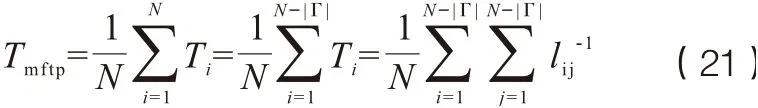
其中l-1

ij为L'的逆矩阵中对应i行j列的元素。

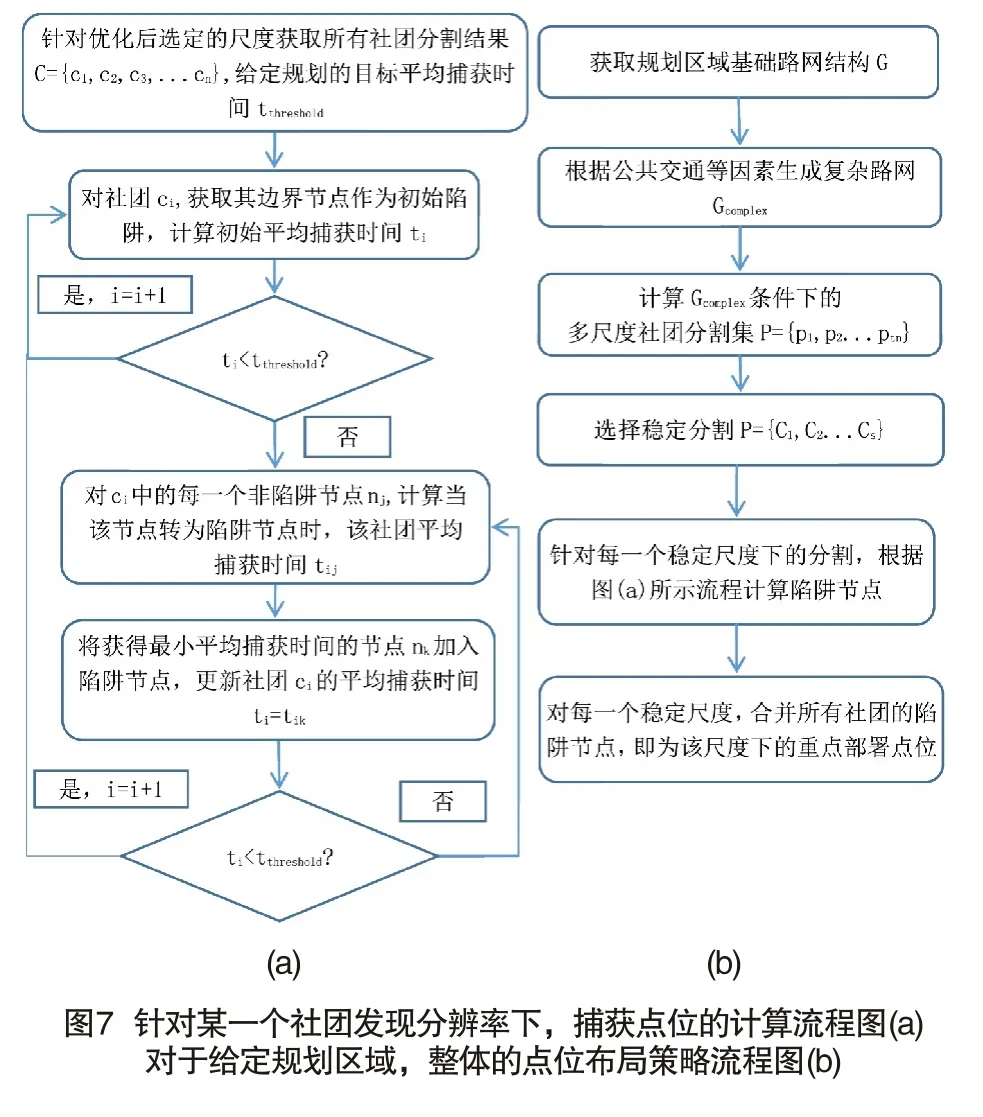
尽管式（21）给出了网络平均捕获时间的计算方法，但必须注意到，在整个计算过程中，涉及大量高阶矩阵运算，难以操作，甚至不具备可行性。因此，前述章节中，对网络进行分割切块成为计算的客观需求。同时，式（21）难以求解其显示表达式，近年来的相关研究也主要集中在特定网络模型[20,21]，对本文所述主题，难以应用更多的启发信息进行优化求解。综合上述因素，本文提出基于贪心策略的点位布局策略，即对每一个社团，每一步将能最小化网络平均捕获时间的节点纳入陷阱节点，直至社团的平均捕获时间达到设计规划要求。针对某一个社团发现分辨率下，捕获点位的计算流程如图7（a）所示。对于给定规划区域，整体的点位布局策略流程如图7（b）所示。

六、实验与分析

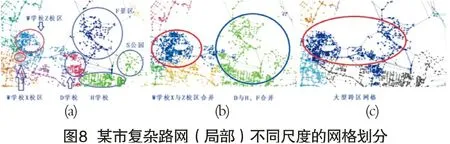
以某市为例，其融合复杂路网节点超过3万个，根据多尺度社团分割，对复杂路网进行网格化划分。在步长为10以下的尺度上，划分的网格在40~50个，反映出小型街道、大型公园景区、大型单位等网格；在步长为10~30的尺度上，划分网格数为30个左右，网格尺度介于大型街道、小型街道联合体、行政区之间；在步长为40~50的尺度上，划分网格为20个左右，已接近实际区级行政区划数量。图8显示了不同尺度社团分割实例。实际上，网格划分与实际行政边界虽然存在一定的关联性，但并非严格对应关系，实质反映的是节点之间的密集关系。如学校W、D和景区F分属不同的三个行政区，但实际上他们之间的连接更为紧密，与周边的连接更为稀疏，更适合作为一个布局圈块结构。

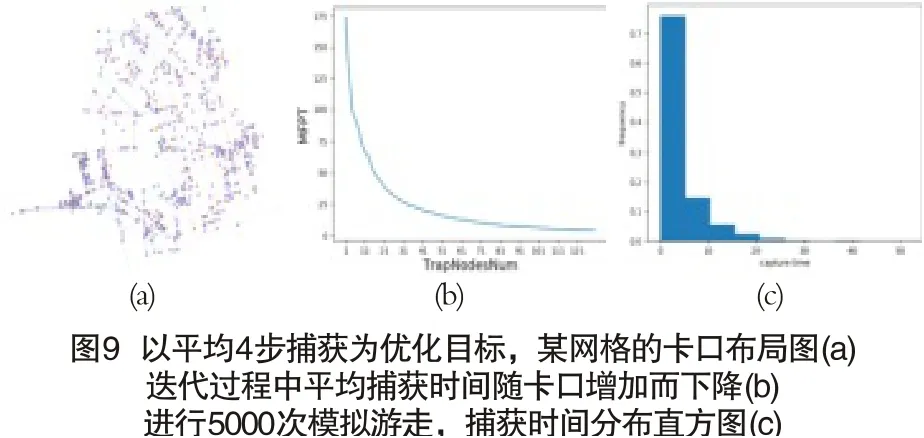
选定网格划分后，每个网格节点数处于数百至数千之间，与原网络数万节点下降1~2个数量级，使得第5章所述定点模型具备计算可行性。以某网格为例，该网格具备节点866个，以28个网格边界节点为初始捕获点，以平均4步捕获为优化目标，经过130轮迭代，平均捕获时间从175降低至4以下，如图9（b）所示，即侦查对象从任意一点出发，以无偏随机游走的方式进行运动，平均经过4个路口即会被智能卡口捕捉到影像。通过对该布点规划进行5000次模拟，平均捕获时间为3.84，标准差为5.05，模拟目标平均每经过3.84个路口即被智能卡口捕获到影像。在经过5个、10个路口的距离内被智能卡口捕获的概率分别为76%和90.5%，如图9（c）所示。图9（a）所示为贪心策略下点位布局，其中绿色节点为网格边界节点，即初始捕获节点，橙色节点为拟部署点位。总拟部署点位占全部节点的18.2%。图9（b）显示，初期，部署少量节点即能快速降低平均捕获时间，前30.7%的点位使得平均捕获时间降低了85.7%，侧面反应出相关建设上的效能边际递减效应。