基于低频无功的柔性直流输电线路纵联保护方案
2022-02-28张怿宁张大海武传健公冶令姣王雪芹
张怿宁, 张大海, 武传健, 公冶令姣, 王雪芹
(1.中国南方电网超高压公司检修试验中心,广州 510663;2.北京交通大学电气工程学院,北京 100044)
柔性直流输电技术应用于新能源并网等项目中,在电网运行中担任着重要的作用。与常规直流技术相比,柔性直流具有便于组网、无换相失败、有功无功独立控制的优势,柔性直流电网成为未来发展的重要方向之一[1-3]。柔性直流输电线路比直流电缆线路故障发生的概率大,且故障电流上升速率大,而模块化多电平(modular multilevel converter, MMC)换流器造价高且脆弱,若不能及时切开故障线路,会对柔性直流设备造成巨大损害甚至进一步破坏电网整体的安全性,所以研究快速切除柔性直流线路的保护方案对提高电网的可靠性具有重要的意义[4-5]。柔性直流线路具有阻尼小、故障电流上升快的特点,因此需要在极短时间内切除故障。以张北四端工程为例,配合混合直流断路器的故障切除时间要求为6 ms,则主保护的出口时间要在3 ms内[6]。
现有主保护原理存在高阻故障难识别的问题,文献[7]所述的行波保护方案最大识别电阻只有100 Ω。文献[8]利用直流电压变化率进行故障识别,但仍存在反应过渡电阻能力差的问题。为此,基于电压、电流变化量乘积的故障识别方案被提出,虽然增加了耐过渡电阻能力,但可靠性仍然受到故障电阻的影响[9]。为保证输电线路的安全运行,后备保护的耐受过渡电阻能力必须得到保证。电流差动保护被广泛采用为后备保护,但是其易受分布电容影响,从而导致保护误判。为解决分布电容导致后备保护的不正确动作的问题,中外学者提出了许多解决方案。文献[10]提出基于故障电流频率的纵联保护方案。文献[11]利用小波变换提取高频暂态电压分量,提出基于区内外暂态能量差异的故障识别方案。上述方案属于频域分析的保护方案,常利用小波分析等数学工具提出多频率故障信息进行故障识别。文献[12-14]从时域分析出发,提出了对分布式电容电流进行补偿的差动保护,但实现较为复杂。文献[15-16]分别从时域和频域方面提出了行波纵联保护,利用行波的特性克服了分布式电容的影响。然而,行波保护存在近端故障难识别、易受噪声影响、存在时间短等缺点,还需进行深入研究。
随着相似度这一数学概念的引入,为直流线路保护方案提供了新思路。文献[17]提出了行波相关性的保护原理,但其研究背景为传统直流工程,且利用的行波信号存在时间较短,难以做到对柔性直流线路进行故障全过程保护。文献[18]针对柔性直流配网提出了基于电流相关系数的保护原理,其应用于线路短、分布电容较小的配电网中具有较好的效果,此方案是否可以应用于长线路、大分布电容的柔性直流输电线路中仍需验证。
由于故障时分布参数充放电的无序性导致分布电容电流的流动规律难以解析,以电流差动保护为代表的后备保护原理依然受分布电容电流的影响。首先分析了线路分布电容电流的频率特性,并提出利用低频无功刻画分布电容电流的流动规律;随后,分析区内、外时低频无功方向的差异性并据此构造故障识别判据;最后,提出了一种基于低频无功方向的纵联保护方案。
1 线路分布参数及低频无功
1.1 分布参数的频率特性
以张北四端柔直输电示范工程为研究对象,其拓扑结构如图1[19]所示。张北工程四端口均采用模块化多电平换流器(modular multilevel converter, MMC),出口处安装有限流电抗器,输电线路采用架空线路。为分析柔性直流工程的故障特性,在线路Line1设置故障点,f1、f2和f3分别为线路Line1的正向内部故障、正向外部故障和反向外部故障。
为分析线路分布参数的频率特性,首先对线路参数进行建模。发生故障时,线路的等效模型如图2所示。

R1、L1、C1分别为单位长度的电阻、电感和电容
根据图1可以得到其输入阻抗为[20]

图1 四端柔性直流输电系统模型[19]
Zoc=Zccothγx
(1)
式(1)中:x为线路长度;Zc为线路特性阻抗;γ为线路传播系数。
将线路具体参数代入后可得
(2)
式(2)中:f为特性阻抗的频率。
当忽略线路电阻时,输入阻抗的频率特性代表了线路电容、电感的频率特性。令
(3)
式(2)中:f2为线路发生串联谐振时的频率。
当频率范围为(0,f2),线路的输入阻抗呈现容性特征[20]。文献[10]详细分析了故障后分布电容电流的频率特性。发生区外故障时,故障电流的频率成分主要是分布电容电流,其频率和行波固有频率一致,其行波固有频率的理论最低值可表示为
(4)
式(4)中:v为故障行波波速度;d为故障距离。
可以看出,分布式电容电流的频率随着故障距离变化,故障距离为200 km时,其频率为330 Hz。因此,分布电容电流的频率高于330 Hz。
因此频率范围同时满足(0,f2)且>fs时,线路分布参数具备相同的特性,即分布电容电流具备了确定的流动规律。可利用此规律构造不受分布电容影响的保护原理。然而,分布电容电流的表达仍然存在困难,因此提出利用直流无功刻画分布电容电流规律的方案。
1.2 直流无功定义
在基于电压源换流器的高压直流输电(voltage source converter based high voltage direct current transmission,VSC-HVDC)系统正常运行期间,它仅传输有功功率,因此,系统的暂态无功几乎不存在。暂态无功的原因主要是由于直流滤波器和平滑电抗器的影响,谐波的总量通常小于额定值的5%。但发生线路故障时系统中的电容成分和电感成分会产生暂态无功电流。
发生线路故障时,其瞬变信号经常是非正弦信号,而非正弦信号的定义方法很多。其中,常用的是基于傅里叶级数的经典暂态无功算法,该算法将暂态无功定义为一定时期内瞬时暂态无功积分的平均值,并被美国国家标准学会(american national standard institute, ANSI)采用[21],其表达式为
(5)
式(5)中:Q为无功功率;k为谐波的阶次;φk为第k次谐波电压与电流的相角差;Uk、Ik分别为谐波电压和电流的有效值。但式(5)具有缺点。由于每个谐波的无功并不完全同号,因此以这种方式获得的暂态电抗不能准确反映暂态电抗的往返过程,并失去其实际的物理意义。
利用有功功率和暂态无功之间的相位差的特性,通过相移法获得暂态无功。因此,新的无功功率表达式为
(6)
式(6)中:u为直流电压;T为采样周期;i为直流电流;t为直流电流采样时间。
1.3 直流无功的暂态特性
根据戴维南定理可以使用等效阻抗和无功功率源对直流系统进行建模,如图3所示。由于线路参数呈现容性,暂态无功方向由故障源到故障点。因此,区内故障暂态过程中,暂态无功的方向如图3(a)所示。而区外故障暂态过程中,暂态无功的方向如图3(b)、图3(c)所示。定义正方向为母线流向线路,可以看出,区内故障期间两侧的暂态无功的方向相同;区外故障时两侧的暂态无功方向相反。综上,暂态无功的方向特性如表1所示。
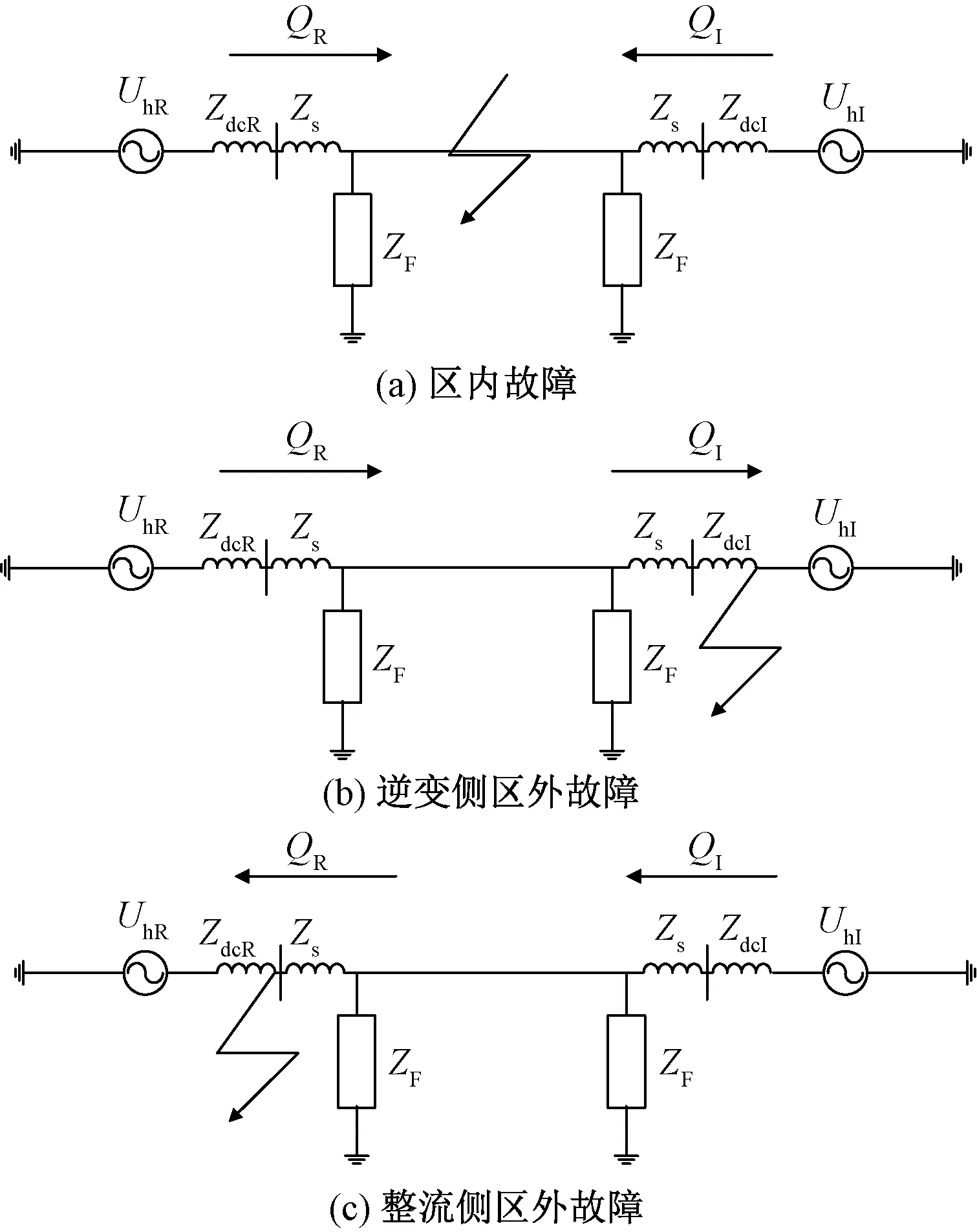
UhR和UhI为线路两侧的无功源;Zs为直流滤波器;ZdcR和ZdcI分别为图1中M和N点换流器的等效电感;ZF为线路等效阻抗;QR和QI分别为M和N点的直流无功功率
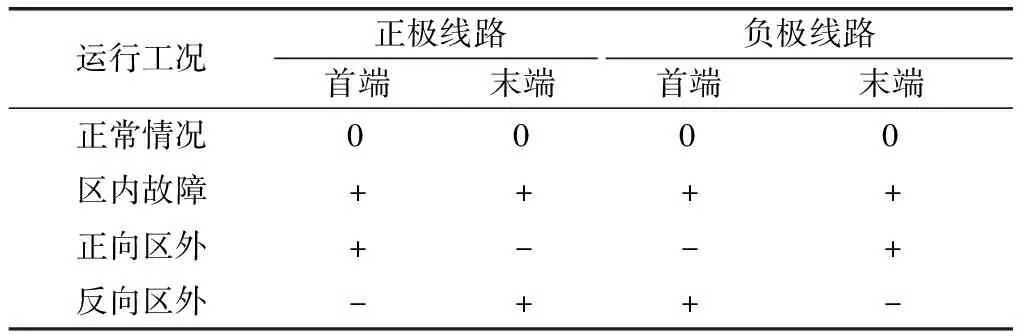
表1 暂态无功方向特性
2 低频无功提取算法
对所求直流无功的频率范围进行计算,由于其频率较低,将其定义为低频无功。根据1.3节可知,低频的暂态无功方向可以区分线路的区内、外故障。但是如何计算直流系统中特定频率的无功是一个难题。希尔伯特变换(Hilbert transform)可以为每个谐波偏移90°,90°偏移不受频率范围的限制,并且相移精度很高。使用时域中的小波变换,可以高效、准确地计算暂态无功。随后使用正交小波分解90°的信号,进一步计算瞬态无功功率。
希尔伯特变换的频率特性可表示为[22]
(7)
(8)

(9)

使用两尺度方程,可以得到尺度系数和小波系数的递推公式为
(10)
式(10)中:h0为低通滤波器系数;h1为高通滤波器系数。
低通滤波器和高通滤波器形成正交镜对称滤波器组。因此,低频无功功率的计算公式为

(11)
式(11)中:c′j,k和d′j,k分别为经过希尔伯特变换后的尺度系数和小波系数;Qi为最低频无功功率;Qj为高频无功功率。
综上,利用小波变换和希尔伯特变换获得低频无功的步骤为:首先,利用式(7)对电压和电流信号执行希尔伯特变换;然后,利用式(9)对信号进行正交小波分解;最后,利用式(11)计算低频无功。
3 保护方案
3.1 启动元件
采用di/dt作为保护启动元件。正常运行情况下,电流突变量非常小(不考虑功率转移)。当直流系统发生故障时,其电流必然发生波动,则电流导数必然发生变化。考虑到运行时存在谐波的情况,将阈值设置为略大于零的数值。当电流出现增加或者减小,且超过设定的阈值时,电流突变量或电流导数启动元件动作。故设置启动判据为
di/dt>kset
(12)
式(12)中:kset为考虑谐波等因素设置的阈值。
3.2 故障识别元件
定义低频暂态无功W(t)为
(13)
分析可知,当发生内部故障时,两侧低频无功的方向相同;当发生外部故障时,两侧低频无功的方向相反。因此,利用低频无功的方向识别区内、外故障,故障识别的判据为
(14)
式(14)中:WR(t)和WI(t)分别为线路整流侧(M端)和逆变侧(N端)的低频无功。
3.3 故障选极元件
故障极的选择是直流保护必不可少的部分。当线路发生故障时,由于两极耦合效应,健康极可能会产生低频暂态无功功率。但是,故障极中的低频暂态无功功率远大于健康极中的低频暂态无功功率。因此,故障极可以通过式(15)选择。
(15)
式(15)中:|Wp|和|Wn|分别为正极低频无功和负极低频无功的绝对值;kset1和kset2为故障选极的阈值,考虑到高阻接地,线路耦合等因素,设置阈值保留一定裕度,选取kset1=1.5,kset2=0.2。
3.4 流程图
根据第2节和第3节的分析,所提保护原理的流程如图4所示。
步骤1首先采集故障电流信号,将电流信号代入保护启动判据[式(12)],若满足条件则保护启动;否则,返回上一步。
步骤2保护启动后,利用希尔伯特变换和小波变换计算低频无功,并向对端发送。当两侧低频无功方向均为正时,判定为区内故障,保护程序进入下一步;否则判定为区外故障,则程序结束,保护不动作。
步骤3根据故障选极判据[式(14)]选择故障极,故障极保护动作,程序结束。
4 仿真验证
4.1 正确性验证
4.1.1 区内双极故障
以图1模型为例进行仿真,在线路Line1设置区内双极金属性短路故障,故障时刻为1.5 s。仿真结果如图5所示。
图5(a)的波形分别为M端和N端测量得到的低频无功,发生故障2 ms后两侧得到低频无功方向均为正。图5(b)的波形为两极线路低频无功的比值,其值范围为0.2~5。综上,低频无功的方向和比值均满足式(14)和式(15),验证了保护原理的正确性。
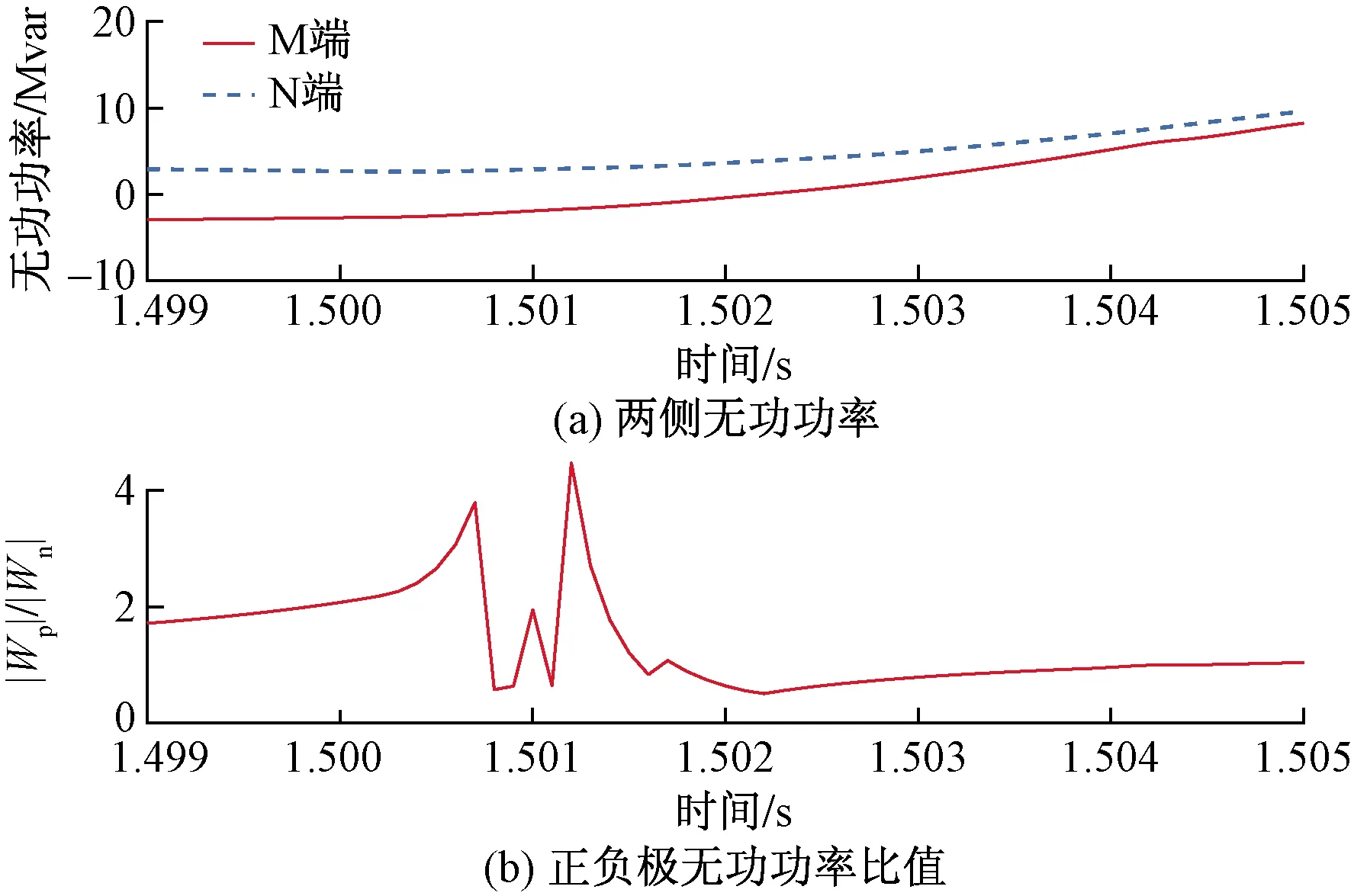
图5 区内双极金属线故障仿真结果
4.1.2 区内单极接地故障
在相同位置设置区内单极接地故障,故障时刻仍为1.5 s,得到故障识别和故障选极的仿真结果如图6。可以看出,故障识别判据(两侧低频无功方向)和故障选极判据(低频无功比值)均满足式(14)和式(15)。因此,所提保护原理可以准确识别区内单极接地故障。

图6 区内单极接地故障的仿真结果
4.1.3 区外双极故障
为了证明所提保护原理在区外故障中的正确性,在Line1中设置了区外双极短路故障。线路两侧低频无功和低频无功的仿真结果如图7所示。

图7 区外双极短路故障的仿真结果
图7(a)可以看出,发生外部故障时,M端测量的低频无功在1.502 s开始变为正向;而N端测量的低频无功在1.502 s开始变为反向。因此,故障后两侧测量的低频无功方向相反,根据式(14)可以判定故障类型为区外故障。另外,图7(b)所示的低频无功的比值满足式(15)。综上,所提保护原理可以准确识别区外故障。
4.2 分布电容的影响分析
由于所使用的低频无功特征考虑了分布电容电流的规律。分布电容的增大不会改变它的频率,即不会影响低频无功的频率段。因此,该保护方案理论上不受分布式电容的影响。为了分析直流线路中分布电容的影响,设置了原始值的8倍的分布电容参数。线路两端测量得到的低频无功的波形如图8所示。
对比图8(a)和图8(b)可知,故障2 ms后两侧低频无功的方向均为正向。表明分布电容的增大并不会改变低频无功的方向,即不会影响所提保护原理的准确动作。

图8 区内双极故障的仿真结果(含分布电容)
为了证明所提保护原理的优越性,将所提保护原理与传统的差动保护方案进行了比较,仿真结果如表2所示,可以看出,电流差动保护在分布电容小于4倍时才可以准确动作,而所提保护方案可以在8倍分布电容时正常工作。因此,所提保护原理不受分布电容的影响。

表2 耐受分布电容能力的对比
4.3 同步误差的影响分析
为了验证同步误差对所提保护原理的影响,设置了约0.1 ms的同步误差,结果如图9所示。结果表明,同步误差不会影响所提出方案的正确性。实际上,所提保护原理只需向对端传输方向信号,对通信的同步的要求较小。

图9 含同步误差区内双极故障的仿真结果
为了证明所提出的保护原理在较大的同步误差下的性能,在仿真数据中增加0~0.5 ms的同步误差。仿真结果如表3所示。仿真结果表明,所提出的保护原理能够在0.5 ms的同步误差下准确识别内部故障。因此,同步误差并不能影响所提保护原理的准确性。

表3 同步误差的仿真结果
4.4 故障电阻的影响分析
抗故障能力是评估保护性能的重要因素。本文模拟了线路Line1上具有不同故障电阻的双极短路故障,以测试所提出的保护原理的耐受故障电阻的能力。故障电阻设置为0~500 Ω,结果如图10所示,可以看出,故障电阻仅影响低频无功的大小,但不会影响其方向。所以,所提保护原理具备一定的耐受故障电阻能力。更多的耐受故障电阻的仿真结果如表4所示。

表4 耐受故障电阻测试的仿真结果
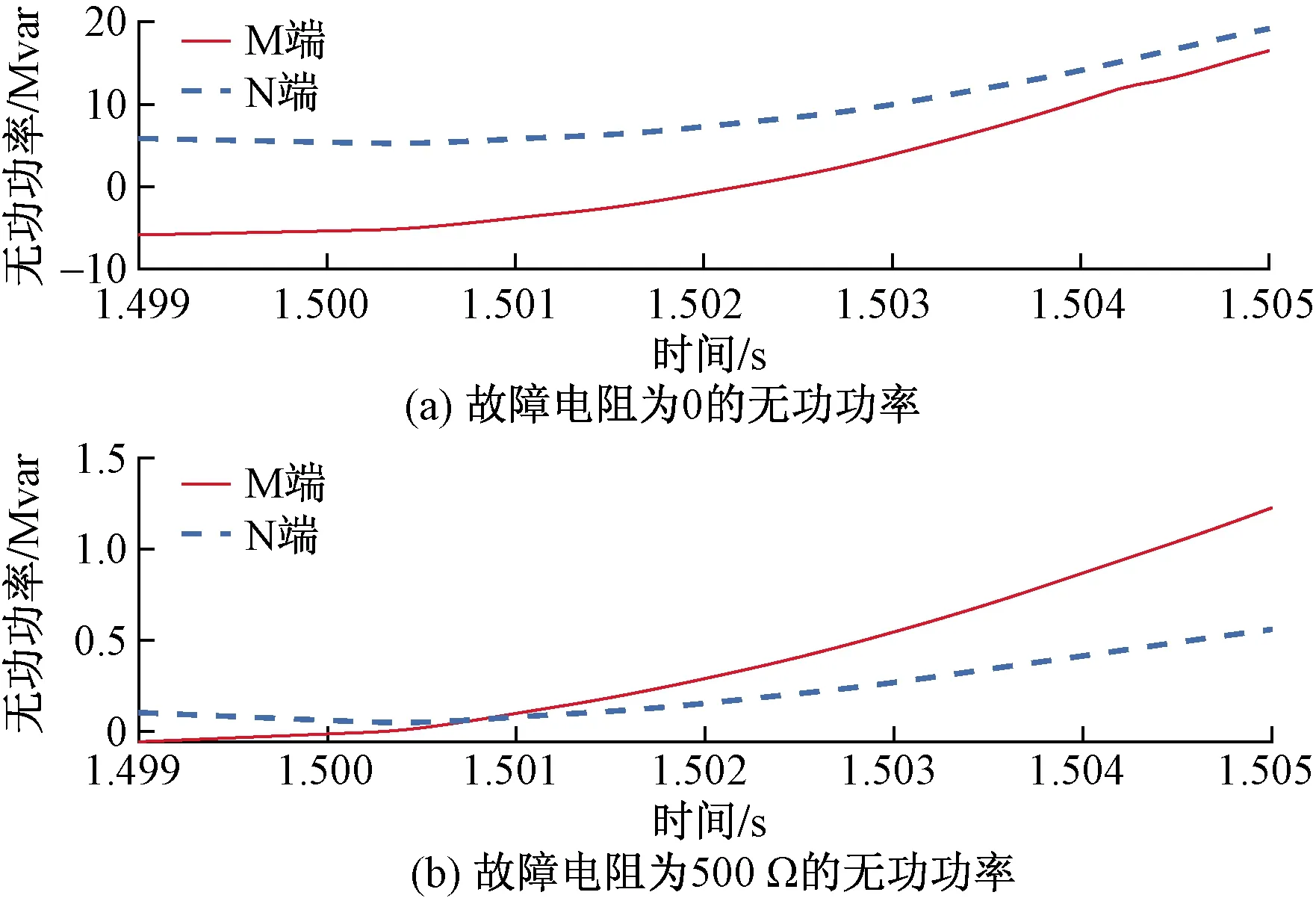
图10 区内双极故障的仿真结果(故障电阻)
4.5 噪声的影响分析
常用信噪比(signal noise ratio, SNR)表示正常信号与噪声信号的关系[14]。信噪比越大,噪声信号越弱。当信噪比达到20 dB时,噪声信号将会淹没原始信号。为了验证所提出的考虑噪声的方法,在每个测试的测量结果中叠加了10 dB的测量噪声,结果如图11所示。

图11 区内双极故障的仿真结果(含噪声)
从图11可以看出,区内故障后两端的低频无功功率可以满足正确动作的条件[WR(t)WI(t)>0]。因此,一定量的噪声对保护性能影响很小。实际上,采用小波变化和希尔伯特变换获取直流低频无功。高频噪声被滤除降低了其对保护的影响,因此本文提出的保护方案具有一定的抗噪声干扰能力。
为了证明所提出保护原理在抗噪声干扰方面的优越性,对电流差动保护原理和所提出的保护原理上分别添加不同噪声比的白噪声进行仿真,仿真结果如表5所示,电流差动保只能忍受30 dB的噪声,而所提保护原理可以在10 dB的噪声干扰下准确动作。

表5 耐噪声干扰能力的测试结果
5 结论
针对直流输电系统提出了一种基于低频无功的纵联保护原理。得出如下结论。
(1)分析并提出了根据线路参数的频率特性描述分布电容电流的流动规律的方法。
(2)提出了利用直流低频无功刻画分布电容电流流动规律的方案,并介绍了小波变换和希尔伯特变换提取低频无功的方法。
(3)与现有的后备保护原理相比,所提出的保护原理不受分布电容电流的影响。仿真结果表明,所提出的保护原理具备较强的耐受故障电阻(500 Ω)、噪声干扰(10 dB)和同步误差(0.5 ms)的能力。
