对BET方程中C的探讨
2022-02-28张伟庆黄滨胡谷平
张伟庆,黄滨,胡谷平
中山大学化学学院,广州 510275
气体吸附BET法测定固态物质比表面积是一个普遍认可的标准方法[1],适用于具有II型(分散的、无孔或大孔固体)和IV型(介孔固体)吸附等温线的固态物质,现在也应用于I型吸附等温线(微孔材料)比表面积的测定。
BET法测定比表面积是大学本科物理化学的经典实验之一,也是目前表征物质表面性质的常用方法,在药学、环境、地学、材料和化学等科学研究中被广泛使用。
Brunauer[2]、Emmett和Teller将单分子层吸附理论扩展到多分子层的II型吸附线,从动力学方法导出了多分子层吸附公式即BET方程[3],方程(算式1)也可用统计热力学方法[4]或其他方法导出[5]。方程有多种数学形式,其中C是与吸附热有关的参数,不同的推导方法C的物理含义可能是不同的[5,6]。

式中:p是吸附气体的压力、p0是吸附气体的饱和蒸汽压力、p/p0是吸附气体的相对压力、V是单位质量样品吸附气体的量、Vm是单位质量样品吸附单层气体的饱和吸附量。
常见的BET方程按所含参数个数可分为二参数、三参数形式[5]:二参数是指C、Vm;三参数是指C、Vm和n(气体吸附在固体表面的分子层数目)。二参数BET方程通常适用于p/p0在0.05–0.35范围内,如果p/p0太低,则不足以建立起多层吸附,当p/p0大于0.35,由于毛细管凝聚现象显著,也会出现偏差;三参数BET方程适用于p/p0在0.35–0.60范围[7]。
以下的探讨都是基于二参数BET方程。
1 C的数学表达式及物理性质
现从BET方程两种推导过程尝试对C的数学表达式及物理性质进行理解。
1.1 用动力学方法推导BET方程时C值的物理性质
用动力学方法推导BET方程时将吸附平衡看成是吸附速度与脱附速度相等,C用算式(2)表达。

式中:a1表示形成第一层吸附时的速度,表示从第一层脱附时的速度,a表示形成第二层及以上各层吸附时的速度,aʹ表示从第二层及以上各层脱附时的速度(假定第二层及以上各层吸附速度都相等且为a;第二层及以上各层脱附速度亦都相等且为aʹ);ε1是吸附气体吸附到样品表面第一层的零点势能,εl是吸附气体吸附到样品表面第二层以上的零点势能(假定第二层以上的吸附分子是液体状态的,即第一层的吸附热为ε1;第二层以上的吸附热为εl,即为凝聚热);k是玻尔兹曼常数;T是用开尔文温标表示的吸附温度。
由于a、a1及与微观分子的物理量的联系尚不明确,对从动力学方法推导出的BET方程中C的物理性质进一步阐明时会很困难[4]。
1.2 用热力学方法推导BET方程时C值的物理性质
用统计热力学方法推导BET方程时C用算式(3)表达:

相比于动力学推导过程,在统计热力学中,所有热力学函数都可以通过配分函数表达出来,对从统计热力学方法推导出的BET方程中的C的物理性质可进一步的阐明[4]。
尽管人们已经推导出不止一种C的数学表达式,但若从其数学表达式着手计算C的确切数值还有困难,目前获得C的方式都还是通过分析BET实验数据得到。
1.3 使C为正值的选点方法
人们分析、处理BET实验数据有时会出现C为负值的情形,这不符合C必须为正值的要求[1]。C是负值在含有微孔的样品中较为常见,其原因是分析数据时简单套用了BET选点p/p0范围在0.05至0.35的要求,没有对数据点进行适当的筛选。多点BET法的p/p0取值范围与样品的孔径密切相关,有学者归纳[8]概括为:对于微孔样品,p/p0取值范围一般为0.01–0.1;对于孔径小于4 nm的介孔分子筛,p/p0取值范围应为0.05–0.2;对于孔径大于4 nm的介孔材料,p/p0取值范围一般为0.05–0.3;对于多级孔分子筛,应根据类型及孔结构特征确定p/p0取值范围。
为了使分析结果C为正值,Rouquerol[9]提出了筛选实验数据点的方法:选取BET数据点时其V(1 −p/p0)值应随着p/p0单调增加,其所依据的数学推导过程参见相关介绍[10]。
Rouquerol方法提醒人们在进行BET实验设定压力点时不应局限于p/p0= 0.05下限的要求,应根据样品情况设定和获得足够多的数据点供后续分析时筛选,如设定实验时p/p0可低至0.01或甚至更低。
在吸附仪配套软件中该方法也被称为BET助手。
2 C与Vm的关系
现尝试就算式(1) BET方程中含有的C和Vm两个参数相互关系探讨如下。
2.1 C值大小与Vm的关系
从对物理吸附过程的理解可以认为样品的Vm(对应比表面积值)大小主要是由其物理形貌决定的;样品C大小是由其表面化学组成及物理性质和被吸附气体性质共同决定的。只从上两点认识出发,描述或判断Vm和C之间关系是困难的,若从吸附热的角度讨论或许有帮助。
在样品吸附气体过程中,固体表面因吸附导致表面能降低和分子间势能降低,会释放出热量,称为吸附热。吸附热的大小可以衡量吸附强弱的程度,吸附热越大,吸附就越强,等温线在低压区就迅速上升。
吸附热大则C也就大、吸附热大则Vm(与比表面积相关)也就大,但若由此推断和比较两个样品的Vm与C的大小关系还是不够充分,这也可以从它们的数学增量关系(见2.2小节)中观察到。
2.2 ∆C值与∆Vm的关系
BET分析的目的是为了求得Vm,进而换算成比表面积值。在处理BET实验数据、选取不同点时常有这样的感觉和困惑:当选取数据点(p/p0和对应的V)时有很小差别就会观察到C发生了很大的变化,而Vm(对应的比表面积)的变化并不显著。文献[11]从数学角度分析和证实了这种感觉,也解释了这种困惑。现将文献中的推导过程简述如下:将算式(1)变换成算式(4)。然后,对算式(4)两边取对数、求导、化简整理并将微分形式改写成增量形式(推导略)即算式(5.1)。


表1 不同p/p0和C时C发生单位增量时对应的Vm的增量变化系数
为了更清晰地说明相互变化的影响,将算式(5.1)改写为算式(5.2)。

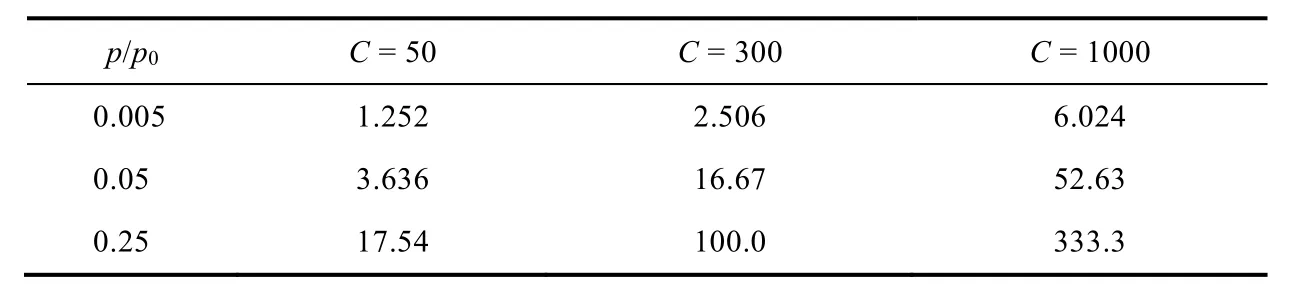
表2 不同p/p0和C时Vm发生单位增量时对应的C的增量变化系数
2.3 C与V等于Vm时对应的p/p0的关系
当V = Vm时,p/p0与C有如算式(6)的简单关系[10],即C越大,达到Vm时的p/p0就越低。在实验室分析测试样品时也可用算式(6)检验实验所设压力点的下限是否合适。

笔者以为或可用此式根据BET方程成立时的p/p0区间要求来估算C的下限(见3.4小节)。
2.4 C与V等于Vm时未被覆盖表面分数的关系
设θ0为样品未被覆盖表面分数。当V = Vm时设样品未被覆盖表面分数为(θ0)m,此时(θ0)m与C有如算式(6.1)关系[12,13](推导略)。

尝试将等于10、100和1000的C分别带入算式(6.1)计算未被覆盖表面分数(θ0)m,分别得到:0.2403、0.0909和0.0307,若换算成当样品吸附量等于单层吸附量时覆盖率时,则分别为75.97%、90.91%和96.93%。
仔细观察算式(6)和(6.1)时会发现其右端完全相同,于是得到新的等式(6.2)。

3 C与吸附等温线形状的关系
BDDT (Brunauer-Deming-Deming-Teller)按照形状将吸附等温线分成5类[4],若用算式(1)即BET方程近似描述吸附等温线时,C的大小与BDDT吸附等温线分类有某种对应关系。
在BET方程中C反映的是吸附热,C大吸附热就大,吸附热大,等温线在低压区就迅速上升;C小吸附热就小,在低压区吸附量就小。具体、简单地说,方程中的C大于2,得到II型吸附等温线,当C相当大时会接近I型吸附等温线;C小于2时得到III型吸附等温线;IV和V型吸附等温线是II型和III型吸附等温线的修正型[13]。
吸附等温线上B点(见3.1小节)和拐点(见3.2小节)是描述吸附等温线形状和类别的关键点,吸附等温线的形状和类别、B点和拐点是否存在和相邻位置关系皆由C的大小决定。
3.1 吸附等温线上的B点
若从吸附等温线图上看,B点是II型吸附等温线直线段的起点[4]。B点表示单层吸附的完成,即B点时的吸附量等于Vm[6],用B点吸附量值计算比表面的方法,称为B点法,它是一种简便求比表面积的方法,只适用于II型等温线比较容易确定B点的情形。
需要注意的是:提出B点法(1937年)的时间早于提出BET方程(1938年)和BDDT分类(1940年)的时间,B点法在比表面分析发展历程中有着重要意义。
3.2 吸附等温线上的拐点
拐点在数学上是指连续曲线的凹弧与凸弧的分界点。若该曲线图形的函数在拐点有二阶导数,则二阶导数在拐点处由正变负或由负变正或不存在。据此,由算式(1)推得吸附等温线拐点坐标[6]分别为算式(7)和算式(8) (推导略)。

由算式(7)和(8)估计不同C区间所对应的p/p0及V/Vm区间范围,将结果列成表3。

表3 不同区间C值对应的拐点坐标及数值区间判断
依据吸附等温线上各点应在0
0的常识,判断当0
3.3 B点和拐点与C大小的关系
当C> 2时曲线上同时存在B点和拐点,吸附等温线上的拐点和B点相邻关系由C的大小决定。B点和拐点的p/p0分别由算式(6)、(7)算得,比较其大小后将结果并列于表4 (推导略)。

表4 判断不同区间C值时B点和拐点所对应p/p0数值差及相邻关系
在实际分析中,B点是人们观察II型吸附等温线时主观认定的,不是推导出来的,有一定的主观随意性。有学者[6]明确指出确定B点位置的难易与吸附等温线拐点(前)的(曲线)形状有关:如果C大,拐点前曲线形状很陡,可精确地确定B点;如果C小,拐点前曲线为圆弧形,B点定位就会很困难,C< 20时不易确定B点。
3.4 对C下限的讨论
C作为吸附质和吸附剂相互作用的一个指标应有一个合理的范围。氮吸附时C通常在50–200之间,C大于200可能表明存在微孔[1]。当C比较小时,虽也可由BET公式计算得到Vm,但此时实验数据的微小变动会引起Vm值较大变化,C接近于1时,无法求算Vm值[14],分析标准[1]也明确指出BET法适用范围是II、IV及I型吸附等温线。
现从数学及物理性质上对二参数BET方程中C的下限做些讨论。
从算式(2)或(3)可看出C是指数函数,指数前因子显然为正值。算式(2)或(3)指数项中的ε1为第一层的吸附热,εl为第二层及以上各层的液化热。第一层的吸附热等于液化热(与第二层及以上各层的液化热相同)与润湿热之和,液化和润湿是放热过程,规定放热为负值,则吸附热的绝对值大于液化热的绝对值,指数项的指数值大于0,指数项则大于1,则指数前因子与指数项之乘积必为正值,据此推断C必为正值。
BET法认为单层吸附完成时的p/p0通常是在0.35以下。若0 C= 1时,算式(1)简化为算式(9)。单纯从数学角度观察,此时BET线性方程可看作是一条平行于横轴的直线。从算式(6)推导出C= 1时达到单层吸附量时的p/p0= 0.5,超出p/p0取值上限,据此推断若二参数BET方程成立,C不应等于1。 假设目前所有已知样品达到单层吸附的最大p/p0是0.35,则可由算式(6)计算出其对应的最小C= [(1 − 0.35)/0.35]2= 169/49 ≈ 3.2。也就是说要使达到单层吸附量时的p/p0不大于0.35,据此推断若二参数BET方程成立,C不应小于3.2。 从以上对算式的逐步分析看,似乎有理由要求不仅C> 0、是正值,甚至可进一步要求C> 3.2。笔者以为,要求C> 0与要求C> 3.2并不矛盾:从C的物理意义出发来要求C> 0是恰当的、必要的,只有在二参数BET方程成立的条件下并能求得C和Vm时,纯粹从数学的角度上才可以进一步要求C> 3.2,笔者以为3.2或可考虑作为二参数BET方程成立时C的合理下限。
