全功率变速抽水蓄能机组快速功率模式小信号建模

史华勃，王渝红，滕予非，陈 刚，孙昕炜，丁理杰

（1. 四川大学电气工程学院，四川省成都市 610065；2. 四川蜀能电力有限公司高新分公司，四川省成都市 610041；3. 国网四川省电力公司电力科学研究院，四川省成都市 610041）

0 引言

随着风电、光伏等可再生能源渗透率的逐渐提高，功率波动、频率调节等问题日渐凸显。变速抽水蓄能机组具有功率双向调节能力，可为解决此类问题提供有效手段，因此得到了广泛关注［1-2］。根据原理不同，变速抽水蓄能机组可分为双馈式和全功率式2 种类型。双馈式机组因其对变流器容量要求低以及具有快速功率调节性能，在大容量场合得到了广泛研究和应用［3-8］。受变流器成本制约，全功率变速抽水蓄能机组（variable-speed pumped storage unit with full-size converter，FSC-VSPSU）尚未得到深入研究和规模应用。与双馈式机组相比，FSCVSPSU 具有更为优秀的调速和应对故障扰动能力［9］。作为双馈式抽水蓄能机组的补充，随着全功率器件成本的降低，FSC-VSPSU 在中小容量场合将具有更广阔的发展前景［10-11］。

对FSC-VSPSU 进行精确的小信号建模，是小扰动稳定分析的基础。通常，经典水轮机模型只能反映额定工况特性，不能反映抽水蓄能机组真实的运行特性。文献［7-8］建立了双馈式抽水蓄能机组仿真模型，但未涉及小信号模型，也未探讨水轮机模型。文献［12］分析了水头和机组负荷对超低频振荡的影响，但采用水轮机传递系数模型，存在系数多、参数非线性变化且不易获取等问题。文献［13-14］提出了各种非线性水轮机模型，但不利于小信号建模，实际系统也未完全按其进行建模。文献［15］建立了双馈式抽水蓄能机组与直驱风电机组联合运行系统小信号模型，但其采用的水轮机模型仍是系数模型，不能满足既能反映机组特性又能快速获取参数的要求。文献［16］研究了FSC-VSPSU 仿真模型，但未涉及水轮机详细控制特性。文献［17］提出了FSC-VSPSU 无功电流优先控制策略，可满足弱电网在故障期间对无功电压的要求。文献［18］验证了抽水蓄能机组功率快速调节特性和电网频率支撑能力。文献［19］通过动模试验验证了抽水蓄能机组在启动、抽水、发电等工况下的有效性。文献［20］研究了抽水蓄能机组虚拟惯性控制策略。文献［21］验证了抽水蓄能机组参与并网光伏电站的功率波动调节的可行性。文献［16-21］均未讨论机组快速功率控制带来的动态稳定问题。在变流器建模方面，文献［22-25］都进行了相关研究，可为FSCVSPSU 变流器小信号建模提供参考。

针对FSC-VSPSU 发电状态，提出了更加适用于抽水蓄能机组特性分析的水轮机模型。对比了经典模型、IEEE 推荐的水轮机模型以及本文提出的模型在额定工况和非额定工况下的机组频率响应，验证了所提出水轮机模型的正确性。结合发电机、励磁系统、调速系统以及变流器模型，构建了FSCVSPSU 小信号模型，并在PSCAD 仿真软件中建立了相应的电磁暂态仿真模型。采用MATLAB 软件求解小信号模型在小扰动下的时域响应，与电磁暂态仿真模型的仿真结果进行对比验证了所提出抽水蓄能机组小信号模型的正确性。

1 FSC-VSPSU 基本结构与控制策略

FSC-VSPSU 结构如附录A 图A1 所示，发电机与电网通过变流器连接。其中发电机采用可变速同步发电机，原动机采用可逆式水泵水轮机。在发电状态下，机组励磁系统、调速系统可采用与常规水电机组相同的控制系统，只要适当整定励磁系统参数，就可不配置电力系统稳定器（power system stabilizer，PSS）。

变流器采用电压源型换流器（voltage source converter，VSC），以及如附录B 图B1 所示的典型dq解耦控制策略。在快速功率模式下，机侧变流器控制有功功率，网侧变流器控制直流电压，调速器控制机组转速或频率。在调速系统频率控制侧可增加机组最优转速控制，提升机组效率。在变流器有功功率控制侧可结合电网频率控制指令、电网优化调度指令等多种控制功能，提升机组对电网的友好性。由于发电机励磁系统已经具有良好的电压控制能力，因此机侧变流器采用零无功控制策略。为支撑电网电压，网侧变流器可采用定交流电压或定无功功率控制。在快速功率控制模式下，能够实现有功功率阶跃调节，对电网功角、频率支撑较好。本文对该控制模式进行小信号建模。

2 FSC-VSPSU 小信号模型

2.1 水轮机模型

在电网安全稳定分析中，式（1）所示的水轮机经典模型得到了广泛应用。

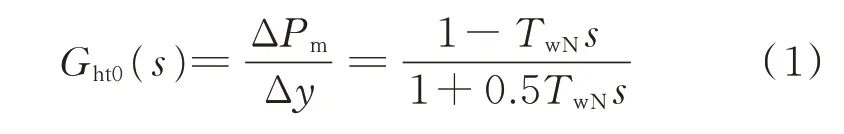
式中:s为拉普拉斯算子；ΔPm为水轮机输出的机械功率偏差量；Δy为导叶开度偏差量；TwN为额定运行点处水锤时间常数；Ght0（s）为经典水轮机传递函数。

当机组在额定工况运行时，该模型能较好地反映原动机特性。但对于抽水蓄能机组，为能辅助电网进行功率或频率调节，往往运行于非额定出力状态，留有较大备用容量。此外，抽水蓄能机组频繁发用电切换，其运行水头也可能偏离额定水头较远，依然采用该模型将带来较大误差甚至错误。IEEE 推荐的水轮机模型［26］（如附录C 图C1 所示）能反映小扰动和大扰动特性，相对更为精确，但其参数不易获取，且不便于小信号分析。

本文采用水轮机刚性水击模型［26］进行研究，并忽略空载损耗和机组效率影响，以额定工况参数为基准值，得到引水管流速、机械功率以及水柱加速度的方程如式（2）所示。

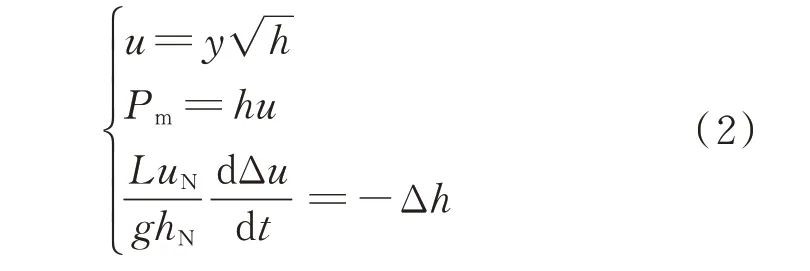
式中:u为水速；uN为额定水速；y为导叶开度；h为导叶处水头；hN为额定水头；Δu和Δh分别为水速偏差量和导叶处水头偏差量；g为重力加速度；Pm为水轮机输出的机械功率；L为水道长度。

将式（2）在运行点处进行泰勒展开，保留线性项，可得如下线性方程组:

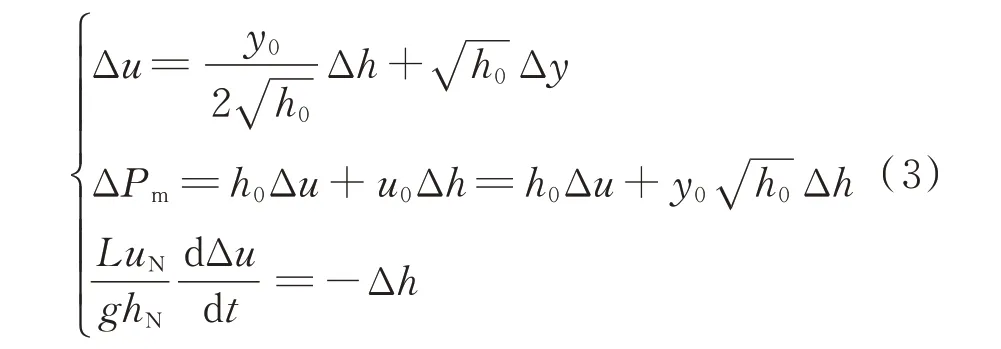
式中:y0、h0、u0分别为导叶开度、水头、水速的初始稳态值。

由式（3）可得:

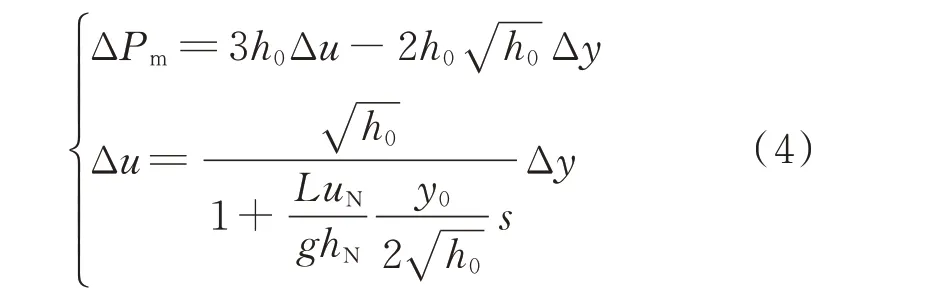
因此，计及初始出力、初始水头的水轮机传递函数Ght（s）为:

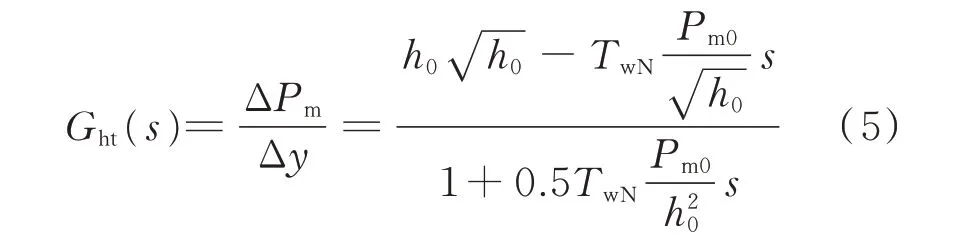
式中:Pm0为水轮机输出机械功率的初始稳态值。

由式（5）与式（1）对比可知，当机组初始运行点处水头h0和输出功率Pm0均为额定值时，式（5）所示模型与式（1）所示的经典模型相同。式（5）所示模型优点在于，可以反映机组初始运行负荷和初始水头的影响，使得机组频率特性分析更加准确。详细推导过程见附录D。

2.2 发电机及其控制系统模型

全功率抽水蓄能机组的发电机仍可采用常规同步发电机模型。为简化分析，励磁系统采用简化模型；调速系统采用详细模型。发电机采用考虑定子电磁暂态的7 阶模型［27］。励磁系统采用1 阶励磁模型［22］，其状态方程为:

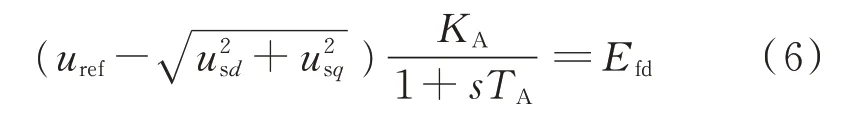
式中:uref为发电机机端电压参考值；usd和usq分别为机端电压d轴和q轴分量；KA和TA分别为励磁系统增益和时间常数；Efd为励磁电压。

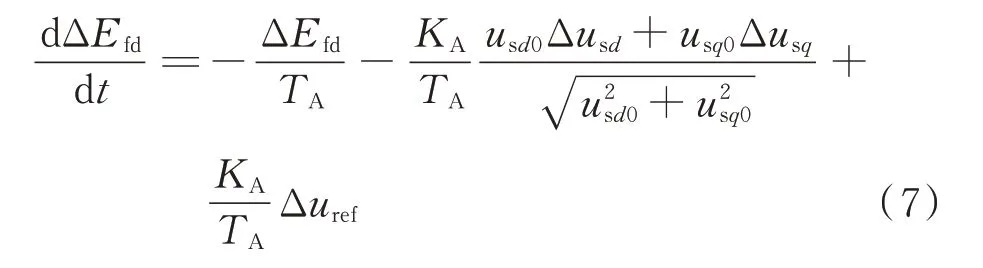
式中:Δuref为发电机机端电压偏差量的参考值；Δusd和Δusq分别为发电机机端电压d轴和q轴分量偏差量；usd0和usq0分别为发电机机端电压d轴和q轴分量初始稳态值；ΔEfd为励磁电压偏差量。

调速系统采用PSASP 7 型调速器［28］，附加调节方式为开度调节，开度偏差接入点在频率控制环节前。频率调节微分增益、伺服机构微分和积分增益均设置为0。单机运行时死区较小，分析中将其忽略，并进一步忽略频率测量环节的惯性和延时。在快速功率模式下，调速系统仍然与常规机组一样进行频率控制。调速系统方程为:

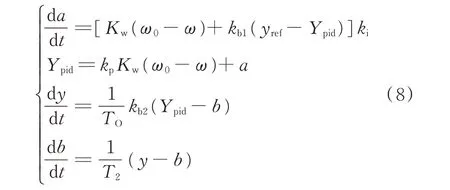
式中:a和b为中间状态变量；ω0和ω分别为发电机转速初值和实际值；kp和ki分别为频率控制比例和积分增益；kb1和kb2分别为导叶开度偏差调节系数和伺服机构比例增益；Ypid为频率控制输出量；TO为水门开启时间常数；T2为功率延时时间；Kw为频率测量放大系数；yref为导叶开度参考值。

调速系统小信号模型为:

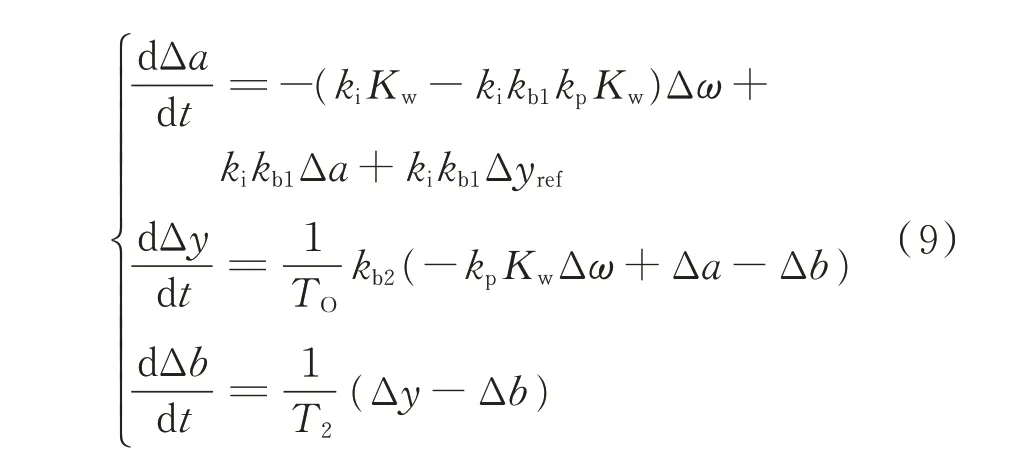
式中:Δa和Δb为中间状态变量偏差量；Δω为发电机转速偏差量；Δyref为导叶开度偏差量的参考值。

2.3 变流器控制系统模型

变流器以机侧变流器为例，忽略电阻损耗，以电流指向VSC 为正方向，VSC 电路状态方程为:

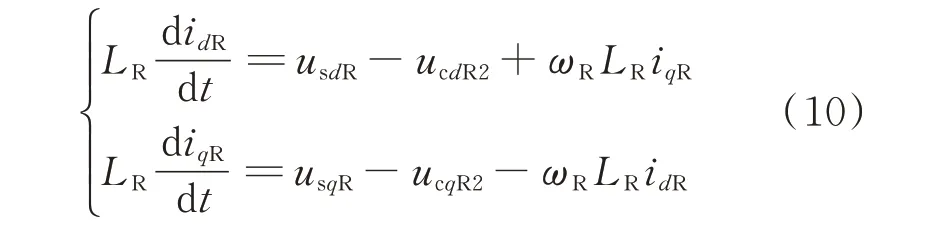
式中:LR为变流器串联电感；idR和iqR分别为变流器电流的d轴分量和q轴分量；usdR和usqR分别为变流器接入电网点电压的d轴和q轴分量；ucdR2和ucqR2分别为变流器阀侧实际电压的d轴分量和q轴分量；ωR为机侧变流器角频率，为保证准确性，ωR应认为是变量。

一直以来，数字城市海量数据可视化、浏览与交互等问题没有得到很好的解决而制约了三维数字城市的广泛应用。该文提出了一种基于四叉树场景管理、模型分块、多细节层次(LOD)的分页数据库的动态调度策略很好地解决了这个问题，并通过实践证明，这种策略确实高效和方便，并已成功应用于天津数字化城市系统建设中。下一步将研究并实现三维数据网络发布与调度，争取而对对加快三维数字化城市的建设和发展起到良好的促进作用。

VSC 控制系统微分代数方程为:

式中:x1、x2、x3、x4为机侧变流器中间状态变量；PrefR、QrefR和PR、QR分别为机侧变流器有功功率、无功功率参考值和实际值；PR2和QR2分别为经过一阶惯性环节滤波后的机侧变流器有功功率和无功功率测量值；idrefR和iqrefR分别为变流器d轴和q轴电流参考值；ucdR和ucqR为机侧变流器阀侧电压的d轴和q轴分量；kδ和Tδ分别为脉宽调制环节增益和调制波周期；Tmd为功率滤波环节延时；kpp和kip分别为有功外环比例、积分增益；kp1和ki1分别为有功内环比例、积分增益；kpq和kiq分别为无功外环比例、积分增益；kp2和ki2分别为无功内环比例、积分增益；ω0R为机侧变流器基准角频率。

参照机侧变流器，可建立网侧变流器数学模型。只须将有功功率相关变量PrefR和Udc换成直流电压参考值和实际值udcref和udc，并建立直流电压方程，就可建立变流器整体模型。接入等值电源后，还需要对电源等值电抗列写微分方程。此外，还需列写发电机与机侧变流器接口模型、网侧变流器与等值电源接口模型。锁相环方程和变流器小信号建模可进一步参考文献［15-18］。

2.4 机组总体小信号模型

结合发电机、励磁系统、调速系统、变流器系统模型，可形成机组总体小信号模型。以ΔX1和ΔX2分别表示发电机控制系统与变流器控制系统状态变量，A1和A2为相应系统的状态矩阵；以ΔU1和ΔU2分别表示发电机和变流器输入变量，B1和B2分别为相应系统的输入矩阵，建立FSC-VSPSU 接入等值电源的全系统小信号模型为:

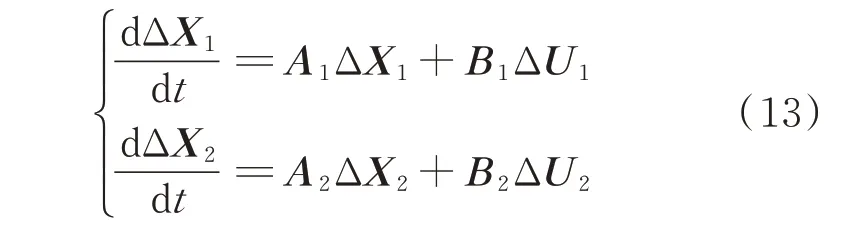
进一步，可构建FSC-VSPSU 接入等值电源的全系统小信号模型为:

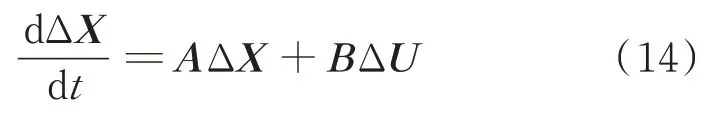
式 中:ΔX=[ΔX1，ΔX2]；ΔU=[ΔU1，ΔU2]；A=[A1，A2]；B=[B1，B2]。具 体 表 达 形 式 见 附 录D 式D（14）至D（16）。

3 小信号模型仿真验证

3.1 水轮机小信号模型仿真验证

以单机带恒阻抗负荷模型（见附录E 图E1）为例，在某时刻切除机组额定容量1%的负荷，测试小扰动特性。其中，发电机额定有功功率为180 MW，惯性时间常数为8.37 s。调速系统仍然采用2.2 节中的模型，水锤时间常数为2 s，调速系统频率控制比例增益为3.5，积分增益为1。设置如下3 种工况:

工况1（额定工况）:扰动前，水轮机在额定工况下运行，即水轮机输出的机械功率Pm0=1.0 p.u.，水头h0=1.0 p.u.。

工况2:扰动前，水轮机输出的机械功率Pm0=0.8 p.u.，水头h0=1.0 p.u.。

工况3:扰动前，水轮机输出的机械功率Pm0=0.8 p.u.，水头h0=0.8 p.u.。

在3 种不同水轮机模型下，频率动态响应如图1所示。

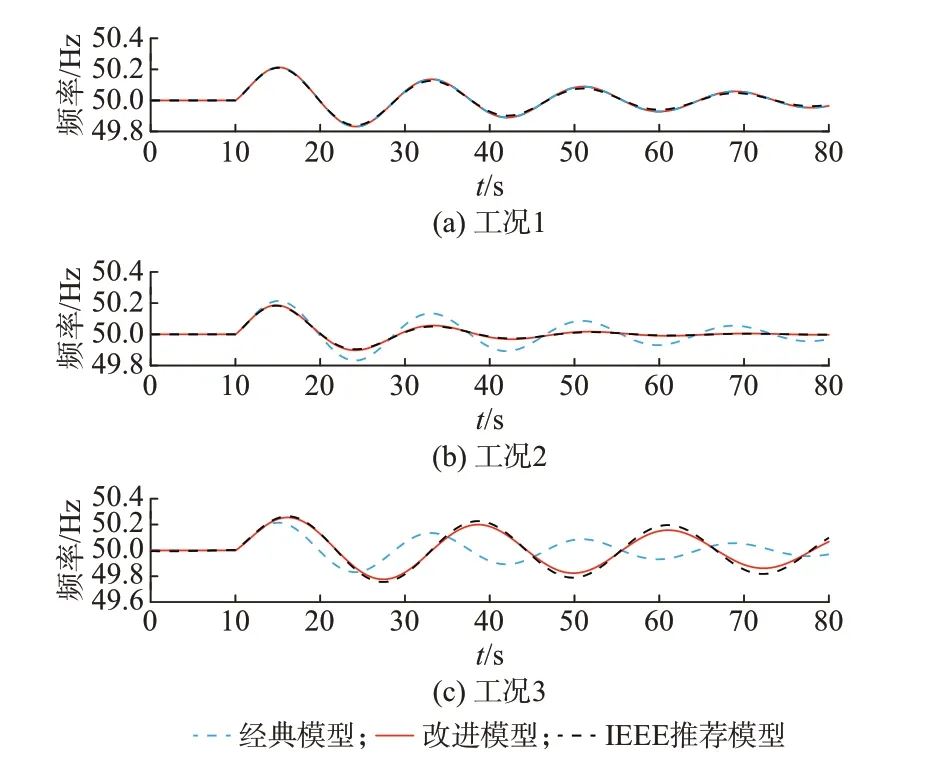
图1 不同水轮机模型下的频率响应Fig.1 Frequency response with different hydraulic turbine models

根据仿真结果，在额定工况下，3 种模型的频率动态响应一致。在工况2 下，改进模型与IEEE 推荐模型响应一致；经典模型频率振荡幅值明显较大，阻尼较弱，相较于改进模型和IEEE 推荐模型，经典模型计算结果更为保守。在工况3 下，改进模型与IEEE 推荐模型振荡模式仍保持一致，振幅略有差异，经典模型振荡模式与其他2 种模型有显著差异，计算结果偏于乐观。

因此，在非额定工况下传统水轮机模型与其他2 种模型响应差异较大。本文提出的计及初始运行工况的改进水轮机模型与IEEE 推荐模型在偏离额定工况不远时的响应一致，偏离额定工况较远时仍能与IEEE 推荐模型响应基本一致。与传统经典模型相比，改进模型能够反映水轮机初始负荷和水头影响，计算结果更为准确，且参数易获取。

3.2 FSC-VSPSU 小信号模型仿真验证

采用PSCAD 软件构建了额定有功功率为5 MW 的FSC-VSPSU 电磁暂态仿真模型，在MATLAB 中建立了相应的小信号模型。模型结构如附录A 图A1 所示，机组关键参数如下所示:发电机额定电压为3.3 kV，额定容量为5.67 MV·A；水轮机惯性时间常数为3.28 s，水锤时间常数为2 s；等值电源额定电压为3.3 kV，等值电感为1 mH；变流器连接电抗为0.6 mH，额定容量为8 MV·A，直流电容为2 000 μF，直流电压为5.2 kV。

水轮机初始负荷4 MW，在5%额定有功功率指令阶跃扰动下，电磁暂态仿真模型和小信号模型响应对比如图2 所示。根据对比结果，小信号模型和电磁暂态仿真模型在电压、转速、变流器电流方面变化趋势相同，波动幅值略有差异，总体上2 种模型响应吻合度较高。在发生扰动后，发电机频率动态调整时间达到60 s 以上。有功功率控制扰动将激发发电机超低频频率振荡，还会引起机端电压超低频振荡，但电压波动幅值极小。

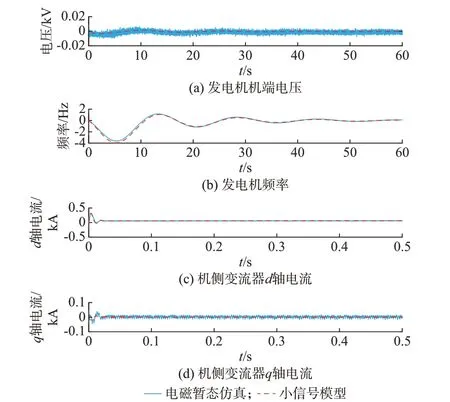
图2 有功阶跃扰动下动态响应Fig.2 Dynamic response under step disturbance of active power

4 机组小信号稳定特性分析

4.1 振荡模态分析

表1 列出了FSC-VSPSU 接入等值电源系统特征值，可见存在6 个振荡模态，分别为超低频模态λ1，低 频 模 态λ2以 及4 个 超 同 步 模 态λ3、λ4、λ5和λ6。其中低频和超同步模态阻尼比均大于10%，超低频模态阻尼比最低，为系统主振荡模态。因此，重点对机组超低频模态进行分析。

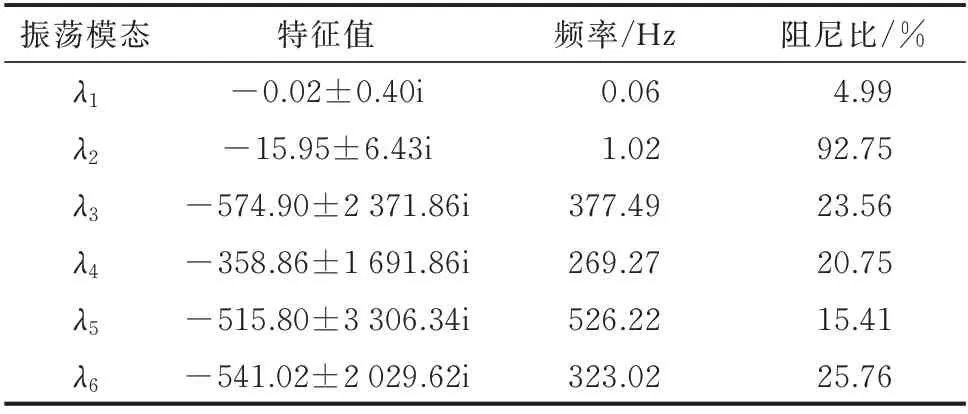
表1 振荡模态计算结果Table1 Calculation results of oscillation modes

超低频模态中各状态变量参与因子如表2 所示，可见机组超低振荡模态只与调速系统状态变量相关，与发电机频率或转速变量强相关，与变流器和励磁系统可以解耦。

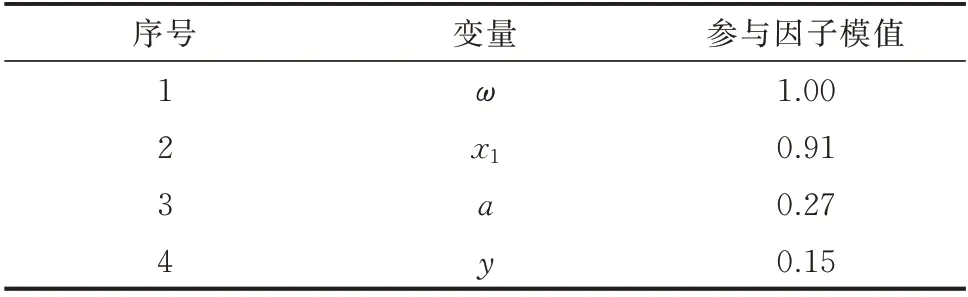
表2 主振荡模态参与因子Table 2 Participation factors of main oscillation mode

4.2 主振荡模态关键影响因素

频率控制增益、机组初始负荷以及机组初始水头对主振模态影响如图3 所示。

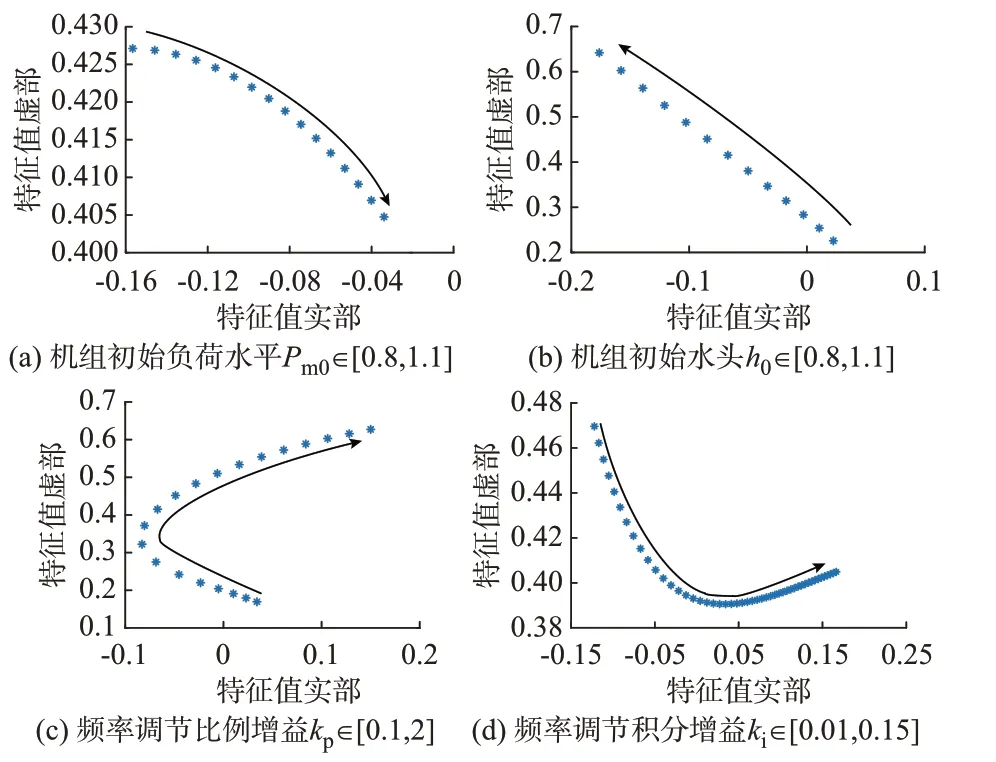
图3 主振荡模态关键影响参数Fig.3 Key influencial parameters of main oscillation mode

随着机组初始负荷增加，超低频模态阻尼水平逐渐降低，振荡频率变化不显著；随着机组初始工作水头逐渐增加，超低频模态阻尼水平逐渐增加，振荡频率逐渐升高；随频率控制比例增益增加，超低频模态阻尼水平呈现先增加后减小趋势，存在显著拐点；随频率控制积分增益增加，超低频模态阻尼水平迅速减小。因此，为保证FSC-VSPSU 在任意工况下均能保持稳定，宜在机组最大运行负荷、最小运行水头工况下整定调速系统参数，并在图3 所示的阻尼特性曲线拐点附近选取合适的频率控制比例增益，并适当减小频率控制积分增益。

5 结语

针对经典水轮机模型不能反映非额定工况运行特性问题，提出了考虑初始运行工况的水轮机小信号模型，能计及水轮机初始负荷和水头影响，较为准确地反映FSC-VSPSU 动态特性。结合发电机、励磁系统、调速系统和变流器模型，构建了FSCVSPSU 接入等值电源系统小信号模型和电磁暂态仿真模型，验证了所建立的小信号模型能够较好地反映FSC-VSPSU 的小扰动动态特性。但论文仅从理论层面对水轮机模型进行了研究，其精确性还需经过现场实测验证。

通过特征值分析，发现机组可能存在超低频振荡模态、低频振荡模态、超同步振荡模态，超低频模态为系统主振荡模态，超低频模态只与调速系统相关，与变流器和励磁系统无关。超低频模态稳定性与机组初始运行负荷和初始运行水头强相关，频率控制比例和积分增益显著影响机组稳定性，因此宜在最大运行负荷、最小运行水头工况下进行调速系统参数整定，并选取合适的频率控制比例增益，适当减小频率控制积分增益。

本文在撰写过程中得到了刘畅、范成围、宋雨妍、喻悦箫、曾雪洋帮助，特此感谢！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。