基于逆变器定频率控制的多分布式电源孤岛检测方法

张 军，张新慧，黄超艺，尹 凡，王苏蓬，吴文浩

（1. 山东理工大学电气与电子工程学院，山东省淄博市 255000；2. 国网泉州供电公司，福建省泉州市 362100；3. 国家电网公司华东分部，上海市 200002）

0 引言

近年来，随着煤炭等不可再生资源的过度消耗和环境污染问题的日益严重，利用太阳能、风能等可再生清洁能源的分布式电源（distributed generator，DG）接入配电网的数量日益增多。当主网供电中断，DG 仍作为孤立电源对负载供电的现象称为孤岛效应。孤岛效应对设备和人员的安全存在重大隐患，因此，当发生孤岛效应时，要求防孤岛保护必须快速切除DG［1-2］。

目前，防孤岛保护方法主要分为远程法、被动法和主动法。远程法通过检测电网侧断路器的状态实现防孤岛保护功能，无检测盲区，对电能质量影响小，但投资成本较高［3］。被动法通过检测并网点电气量是否越限实现防孤岛保护功能，主要分为电压/频率检测法［4-5］、电压谐波检测法［6-7］和电压相位突变检测法［8］。被动法实现简单、投资成本低、对电能质量影响小，但其动作阈值难以整定。主动法通过注入扰动量实现防孤岛保护功能，主要分为主动频率偏移法［9］（active frequency drift，AFD）、Sandia 频率偏移法［10］（Sandia frequency shift，SFS）、滑模频率偏移 法［11-12］（slip-mode frequency shift，SMS）、有 功 功率扰动法［13-14］和无功功率扰动法［15-17］。文献［18］利用向dq轴注入低频扰动消除检测盲区；文献［19］通过改进SMS 法缩小检测盲区；文献［20］利用向中性点注入20 Hz 的低频电流，检测低频电压、电流的变化特征来实现孤岛检测功能；文献［21-22］通过注入电压扰动，辨识孤岛的阻抗值进行孤岛检测。扰动并网点电压的频率或相位会注入较大的谐波，有功功率扰动法会影响DG 发电效率，而无功功率扰动法仅向并网点注入周期性的无功功率，因而对电能质量的影响较小。此外，小波变换和神经网络也在孤岛检测中广泛应用［23-25］。

对于多DG 孤岛检测，传统主动法易发生各逆变器注入扰动量相对减小或相互抵消的稀释效应。文献［26-27］中提出可采用SFS 和SMS 混用的检测方法；文献［28］采用具有下垂特性的锁相环控制逆变器向并网点注入扰动量。上述两种检测方法均利用正反馈扰动的特点以避免稀释效应，但当孤岛频率偏移较小时，易引起逆变器对频率偏移方向的误判，导致扰动方向相反，产生稀释效应。

为了解决上述问题，本文提出利用主/从逆变器相互配合的多DG 孤岛检测方法。该方法任选一台逆变器作为主逆变器，利用正弦脉宽调制技术控制其输出电压的频率为额定频率，其他锁相环控制的逆变器作为从逆变器，其输出电压的频率与并网点频率保持一致。在主逆变器稳定孤岛频率后，由无功功率负反馈控制从逆变器，使其输出无功功率的实际值围绕设定值波动，因此主逆变器能够优先输出或吸收无功功率，从而消除孤岛检测的稀释效应，实现多DG 孤岛检测。

1 多DG 孤岛检测方法的稀释效应分析

当DG 并网运行时，如附录A 图A1 所示，负载所需的功率由电网和DG 共同提供，即

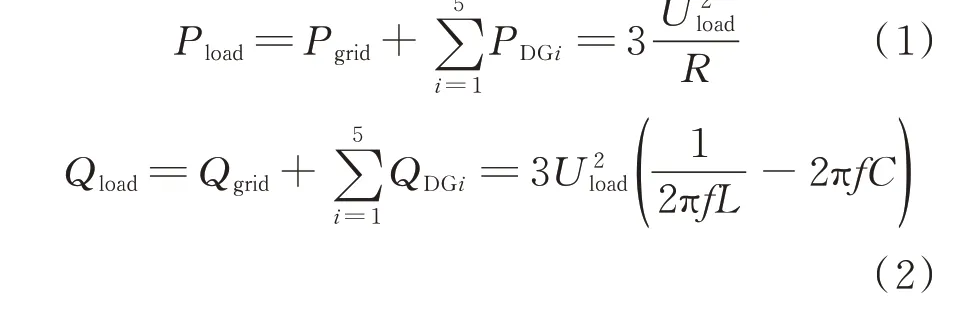
式中:Pgrid和PDGi分别为电网和第i个DG 输出的有功功率；Qgrid和QDGi分别为电网和第i个DG 输出的无功功率；Pload和Qload分别为负载消耗的有功功率和无功功率；Uload和f分别为孤岛相电压的有效值和频率；R、L、C分别为负载的等效电阻、等效电感和等效电容。

将式（1）代入式（2），化简后可得:

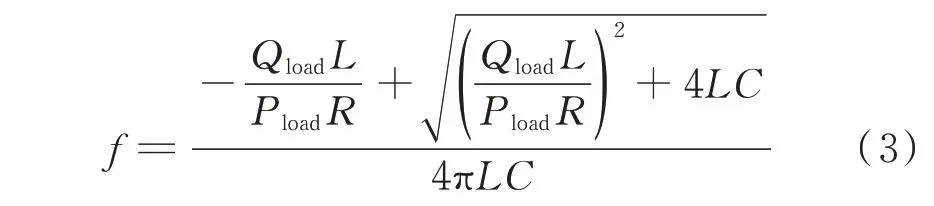
发生孤岛效应时，若系统中仅有一台逆变器，则孤岛缺额或剩余的有功或无功功率仅由一台逆变器输出或吸收。由式（1）可知，若孤岛有功功率不足或过剩，则孤岛电压降低或升高；由式（3）可知，若孤岛有功功率平衡、无功功率存在缺额或过剩，则孤岛频率升高或降低。因此，传统孤岛检测方法可通过扰动有功/无功功率平衡引起电压/频率越限，也可直接扰动频率使其越限，从而检测到孤岛效应，即单DG 孤岛检测不存在稀释效应。

在多DG 孤岛检测中，因各逆变器之间无通信联系，难以保证同向扰动，易导致输出扰动量增加和减小的逆变器同时存在，从而产生稀释效应，增加孤岛检测难度。文献［26］分析了AFD 法、SFS 法和SMS 法产生稀释效应的原因:采用AFD 法控制的逆变器，其频率的扰动方向为预先设定，若各逆变器中频率的扰动方向不同，即扰动频率升高和降低的逆变器同时存在，会导致注入孤岛的扰动量相互抵消；而采用SFS 或SMS 法控制的逆变器，若孤岛频率偏移较小，易导致部分逆变器对频率偏移方向的误判，其注入的扰动量方向与期望方向相反，使得扰动量相互抵消。采用上述方法进行孤岛检测时，均会产生扰动量相互抵消的稀释效应，导致无法检测到孤岛效应。

文献［27］分析了多DG 孤岛检测中无功功率扰动法产生稀释效应的两种形式:1）在负载所需无功功率保持不变的情况下，与单DG 孤岛相比，多DG孤岛中各逆变器承担的无功功率缺额明显减少，即产生稀释效应；2）当各逆变器注入的无功功率扰动量无法保持同向扰动，即输出与吸收无功功率的逆变器同时存在时，注入孤岛的扰动量相互抵消，即产生稀释效应。

根据上述分析，对于多DG 孤岛检测，由于各逆变器之间无通信联系，扰动量难以保持同向，因此易产生稀释效应。对于锁相环控制的逆变器，若将孤岛频率稳定在一定范围内，则该逆变器输出电压的相位不会发生突变，此时可以利用无功功率负反馈控制逆变器输出电流的相位，使其输出无功功率的实际值接近设定值，从而消除稀释效应，实现多DG孤岛检测。

2 控制逆变器频率的孤岛检测原理分析

2.1 逆变器工作原理

本文以A 相为例分析孤岛检测时电气量的变化过程，B、C 相的变化过程与A 相一致，仅存在初相位的不同。假设并网点A 相电压初相位为0，逆变器输出侧A 相电压初相位为δ，由图1 可知，其并网 电 流˙ 为:

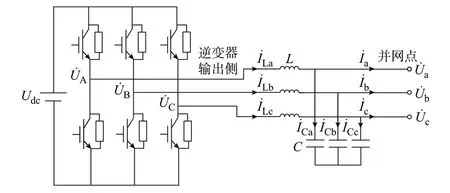
图1 三相全桥逆变器主电路Fig.1 Main circuit of three-phase full-bridge inverter

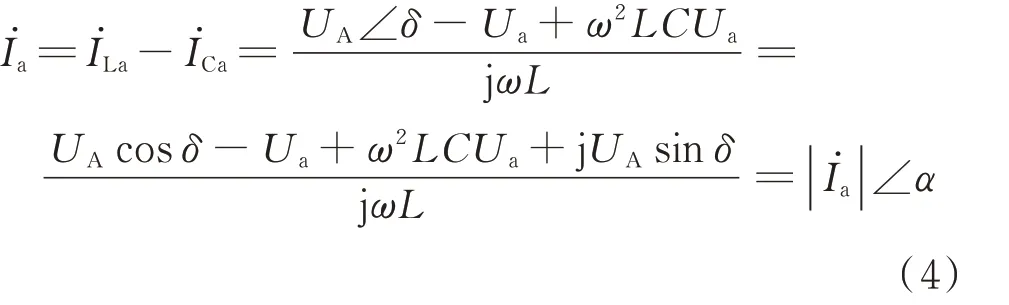
由1.2 节和附录A 图A2（c）可知，若发生多DG孤岛效应，且孤岛存在无功功率缺额，则各DG 共同输出无功功率，即孤岛的无功功率缺额被各DG 均分，导致孤岛频率上升速度较慢甚至难以越限，产生稀释效应。

为了消除稀释效应，本文提出逆变器的定频率控制方法，即通过控制的相位来稳定孤岛频率，进而消除稀释效应，实现多DG 孤岛检测。

2.2 主逆变器的定频率控制

在多DG 孤岛检测中，由1.2 节的分析可知，传统主动法均存在稀释效应。为了消除稀释效应，本文提出主/从逆变器相互配合的多DG 孤岛检测方法。该方法任选一台逆变器作为主逆变器，根据孤岛无功功率平衡与频率的关系，主逆变器采用基于正弦脉宽调制技术的定频率控制方式，其调制波由周期为0.02 s、幅值为2π 的锯齿波产生，从而控制主逆变器输出电压的频率为额定频率；而其他逆变器作为从逆变器，仍然采用锁相环控制方式。在主逆变器稳定孤岛频率后，从逆变器恢复正常运行状态，因此孤岛所需的无功功率仅由主逆变器提供，从而有效地消除了稀释效应。主逆变器检测到孤岛效应并切除后，将打破孤岛的有功功率平衡，使得各从逆变器可利用被动法检测到孤岛效应并切除。主/从逆变器的控制原理框图如图2 所示，其中Ure和fre分别为DG 并网点电压和频率的瞬时值。

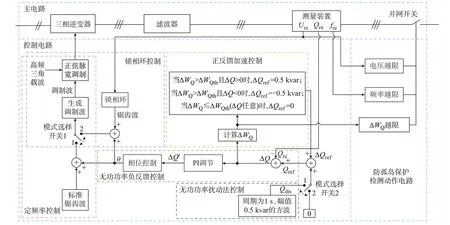
图2 主/从逆变器的控制原理框图Fig.2 Block diagram of control principle of main/slave inverter

主/从逆变器的控制电路主要包括以下几部分。

1）无功功率负反馈控制

将逆变器输出无功功率的设定值Qref与实际值Qre的差值记为ΔQ，经比例-积分（PI）调节后得到ΔQ′，进而产生控制锯齿波相位的偏移量θ，即图2 中相位控制 模 块。θ通过控 制的相位 来控制的相位，实现对逆变器输出无功功率的控制，其中偏移量θ=arcsin(ΔQ′/(3UI))，如附录A 图A3 所示，U和I分别为DG 输出电压和输出电流的有效值。

2）定频率控制

主逆变器在并网运行和孤岛检测时均采用定频率控制方式，其锯齿波的频率和相位仅受偏移量θ的控制。并网运行时，当主逆变器并网点电压的相位在第2 周期发生超前突变时，其锯齿波、调制波的变化如附录A 图A4 所示。由附录A 图A2（a）可知，由于滤波器的存在，逆变器输出侧电压的相位超前并网点电压的相位δ角度，正常运行时δ非常小，为了简化分析，假设δ=0。

由无功功率负反馈控制可知，电网电压相位的突变导致主逆变器的ΔQ偏离零值，将产生偏移量θ来控制锯齿波的相位，实现主逆变器运行在单位功率因数状态。

在实际运行中，由于ΔQ′持续变化，且ΔQ′、θ和锯齿波相位的突变点一一对应，因此锯齿波的相位突变具有突变点多、突变量小的特点，附录A 图A4中仅放大显示了其中2 个突变点。

3）锁相环控制

锁相环控制是根据逆变器并网点电压的相位生成锯齿波，进而生成正弦调制波。与主逆变器的锯齿波相比，该锯齿波的特点是其频率和相位不仅受偏移量θ的影响，且与并网点电压的频率和相位有关。

4）无功功率扰动法控制

为了避免因孤岛功率平衡导致的孤岛检测盲区，文献［16，29］根据孤岛负载的品质因数和DG 输出的有功功率计算扰动孤岛频率越限的无功功率扰动量幅值Qdis1和Qdis2，分别如式（5）、式（6）所示。

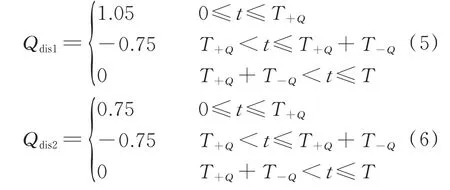
式 中:Qdis1和Qdis2的 单 位 为kvar；T+Q、T-Q和T分 别为正向扰动时长、反向扰动时长和扰动周期，T+Q和T-Q均取0.2 s，T取2 s。

本文任选一台逆变器采用无功功率扰动法打破孤岛功率平衡，与文献［16］和文献［29］中需扰动孤岛频率越限不同，本文的扰动量仅用于打破孤岛的无功功率平衡，因此可减小其扰动量的幅值Qdis，如式（7）所示。

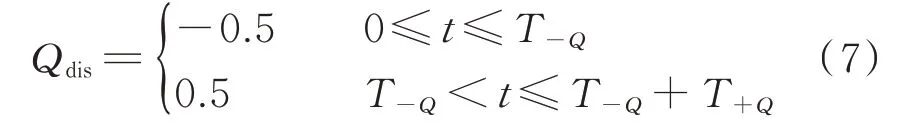
式中:Qdis的单位为kvar；T+Q、T-Q均取0.5 s。

5）正反馈加速控制

并网运行时，主/从逆变器的ΔQ均围绕零值波动；发生孤岛效应时，主逆变器的ΔQ偏离零值，对|ΔQ|进行积分处理，记为ΔWQ，其幅值表征了ΔQ偏离零值的时长和偏离程度。为了缩短孤岛检测时间，设定正反馈加速控制的动作阈值ΔWQth，当ΔWQ＞ΔWQth时，若ΔQ＞0，则逆变器的Qref增加ΔQref，若ΔQ＜0，则减小ΔQref；当ΔWQ≤ΔWQth时，无论ΔQ为何值，均不注入正反馈扰动量。因ΔWQth过小易导致逆变器向并网点注入不必要的正反馈扰动量，而ΔWQth过大则会降低本文方法的检测速度，综 合 考 虑 以 上 因 素，将ΔWQth设 定 为30 var·s。若ΔQref过小则无法实现正反馈扰动的功能，而ΔQref过大将导致ΔWQ增速过快，引起误动作，综合考虑以上因素，将ΔQref设定为0.5 kvar。

因此，采用正反馈加速控制可加大孤岛的无功功率不平衡度、提高ΔWQ的上升速度和缩短孤岛的检测时间。

2.3 多DG 孤岛检测方法

对于多DG 孤岛，本文采用主/从逆变器相互配合的孤岛检测方法。

对于主逆变器，由于其锯齿波的频率和相位仅受偏移量θ的控制，因此θ变化时将控制主逆变器输出电压的频率和相位发生变化，假设一个周期内θ减小Δθ，则主逆变器输出电压的频率将升高（50Δθ/360）Hz；对于从逆变器，由于其锯齿波的频率和相位不仅受偏移量θ的控制，且与并网点电压的频率和相位有关，因此θ不为零时将控制从逆变器输出电压的频率和相位发生变化，假设偏移量θ为-θ1，则输出电压的频率将升高（50θ1/360）Hz。

由2.2 节中对无功功率扰动法控制的分析可知，发生孤岛效应时，该控制能够打破孤岛的无功功率平衡，导致主/从逆变器的ΔQ偏离零值，使得主/从逆变器的|ΔQ′|和|θ|持续增大；当主逆变器的θ到达极值并保持不变时（如附录A 图A3 所示），即Δθ为零，则其锯齿波的相位不会发生突变，因此主逆变器能够将孤岛频率钳位至50 Hz，其稳定孤岛频率的过程如附录A 图A5 所示。

主逆变器稳定孤岛频率后，从逆变器将利用其θ控制ΔQ恢复正常稳定运行状态，使得孤岛缺额或剩余的无功功率仅由主逆变器输出或吸收，从而消除稀释效应。

由于孤岛的无功功率不平衡将导致主逆变器的ΔWQ逐渐增大，因此可设定切除主逆变器的动作阈值ΔWQset，当ΔWQ＞ΔWQset时，判定系统发生孤岛效应并切除主逆变器，从而打破孤岛的有功功率平衡，使得从逆变器可利用被动法检测到孤岛效应并切除各从逆变器。若ΔWQset过小可能导致保护的误动作，ΔWQset过大则会降低检测速度，导致孤岛检测时间过长，综合考虑上述影响因素，将ΔWQset设定为50 var·s。利用本文方法检测多DG 孤岛的过程如图3 所示，图中各参数为主逆变器的参数。

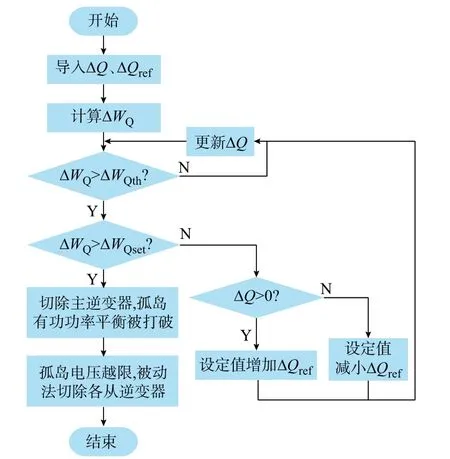
图3 本文孤岛检测方法流程图Fig.3 Flow chart of proposed islanding detection method

综上所述，本文利用定频率控制的主逆变器消除多DG 孤岛检测的稀释效应，利用无功功率扰动法避免孤岛功率完全平衡的检测盲区，实现多DG孤岛的无盲区检测。

此外，为了避免稀释效应，应确保主逆变器稳定、可靠地运行，即主逆变器因人为拉闸或故障停机时，应将其他某台从逆变器的控制方式切换为定频率控制方式，作为主逆变器并网运行；对于停机的主逆变器，在恢复运行后将采用锁相环控制方式，作为从逆变器并网运行。

当主逆变器检测到孤岛效应时，为了避免因从逆变器过多而无法扰动孤岛电压越限，应控制主逆变器向孤岛内注入频率扰动量，使孤岛频率越限，则主/从逆变器均利用被动法检测孤岛效应并切除。

2.4 盲区分析

由第1 章的分析可知，无功功率扰动法可打破孤岛的无功功率平衡，缩小孤岛检测盲区。本文方法的无功功率扰动量Qdis如式（7）所示，当采用无功功率扰动法的逆变器向孤岛注入扰动量时，根据2.2节中对主逆变器的分析可知，主逆变器会注入与扰动量幅值相等、方向相反的无功功率，即Qre=Qre0-Qdis，其中Qre0为未注入扰动量前主逆变器输出无功功率的实际值。

为了分析本文方法的检测盲区，假设主逆变器输出无功功率的设定值Qref有3 种情况，依次为0.3、0 和-0.3，则ΔQ=Qref-Qre=Qref-Qre0+Qdis，由于Qre0为常数，因此不影响ΔQ的变化趋势，可假设Qre0=0，则基于ΔQ-t的盲区如附录A 图A6 所示，因此在扰动量的一个周期T内，无论主逆变器的Qref和Qre0为何值，总有T/2 周期保证其|ΔQ|≥0.5 kvar。根据2.2 节正反馈加速控制可知，孤岛无功功率的不平衡程度越大，主逆变器的|ΔQ|越大，其ΔWQ增速越快，从而越容易检测到孤岛效应，由此可知，主逆变器|ΔQ|=0.5 kvar 时，最难检测到孤岛效应。

3 仿真验证

为了验证本文方法检测孤岛方法的有效性，利用MATLAB/Simulink 搭建仿真模型，分别对单DG、多DG 构成的孤岛进行检测。假设系统中有5 台DG，依次记为DG1 至DG5，其中Udc=800 V、UN=220 V、f=50 Hz、ΔWQth=30 var·s、ΔWQset=50 var·s、ΔQref=0.5 kvar，各DG 逆变器采用的控制方式如表1 所示。

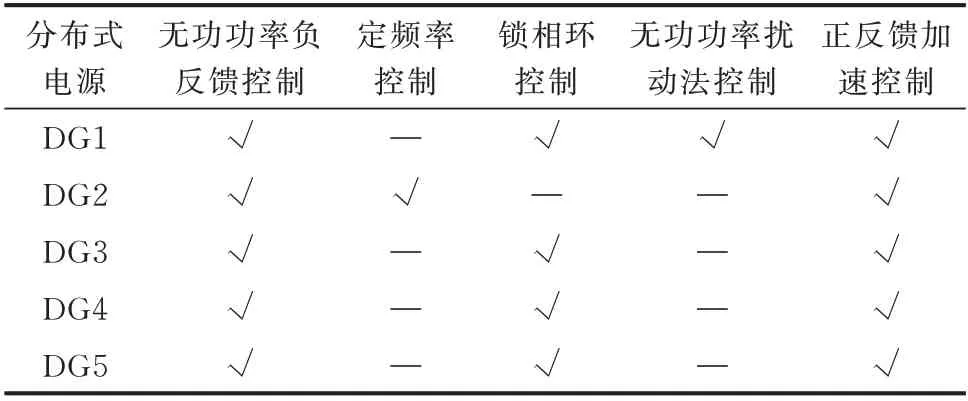
表1 各分布式电源的逆变器控制方式Table 1 Inverter control mode of each DG

3.1 单DG 接入配电网的孤岛检测

当孤岛仅由DG2 和负载构成时，为了缩小孤岛检测盲区，DG2 的逆变器采用带正反馈加速控制的无功功率扰动法。假设电网在0.6 s 发生孤岛效应，电网与DG2 输出无功功率波形如图4 所示，由于DG2 的逆变器采用正反馈加速控制，且其ΔQ偏离零值，导致其ΔWQ逐渐增大，并在0.69 s 时大于ΔWQth，因此其Qref会发生突变；电网与DG2 输出电压的波形如附录A 图A7 所示。

由图4 可知，发生孤岛效应时，孤岛无功功率过剩，导致DG2 的Qre无法与Qref保持一致，使得ΔQ不为零，根据仿真数据可得，孤岛运行期间DG2 的Qre为-0.432 kvar，则DG2 的ΔQ为0.432 kvar，使 得ΔWQ逐渐增大并达到ΔWQset；由仿真结果可知，在0.720 s 时检测到孤岛效应并切除DG2，如附录A 图A7 所示，因此，孤岛检测时间为0.120 s（0.6 s 时发生孤岛效应）。根据2.4 节可知，利用无功功率扰动法能够打破孤岛的无功功率平衡，实现对单DG 孤岛的无盲区检测。

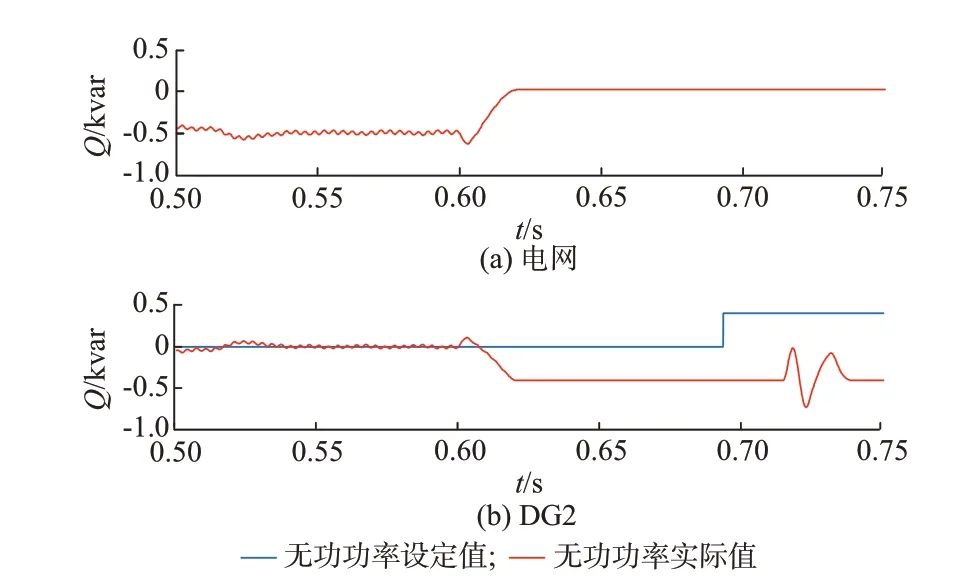
图4 电网和DG2 输出无功功率波形Fig.4 Output reactive power waveforms of power grid and DG2

3.2 多DG 接入配电网的孤岛检测

3.2.1 无功功率扰动法

当发生单DG 孤岛效应时，利用无功功率扰动法可快速地检测到孤岛效应［15-17］，与远程法和被动法相比，该方法具有投资小、检测盲区小的优点；与AFD 法、SFS 法和SMS 法等其他主 动法相比，该方法对并网点的电能质量影响更小；与有功功率扰动法相比，该方法不会影响光伏电源的发电效率，因此，选择无功功率扰动法与本文方法进行仿真，对比分析多DG 孤岛检测的有效性。

假设电网在0.6 s 发生孤岛效应，各DG 的逆变器均为锁相环控制方式，且DG1 在0.7 s 向并网点注入0.5 kvar 的无功功率扰动量，电网与各DG 输出无功功率波形如附录A 图A8 所示。

由附录A 图A8 可知，DG1 的Qref在0.7 s 时变为0.5 kvar，导致孤岛无功功率过剩；根据仿真数据可得，孤岛运行期间DG1 至DG5 的Qre依次为0.392、-0.116、-0.091、-0.091、-0.091 kvar，其中负号表示逆变器吸收无功功率，则DG1 至DG5 的ΔQ依次为0.108、0.116、0.091、0.091、0.091 kvar，即DG2、DG3、DG4 和DG5 共同吸收DG1 注入孤岛的无功功率，由此引起的稀释效应导致各逆变器无法检测到孤岛效应。

3.2.2 控制逆变器频率的检测方法

为了验证本文方法检测多DG 孤岛的有效性，分别在负载性质为纯阻性、感性或容性的孤岛中进行仿真验证，仿真条件如表2 所示。

表2 不同负载性质下的仿真参数Table 2 Simulation parameters with different loadcharacteristics

仿真1 至3 中各DG 输出无功功率波形分别如图5、附录A 图A9 和图A10 所示，DG2 输出无功功率设定值发生突变的原因与3.1 节单DG 孤岛检测中图4 相同；仿真1 中各DG 输出电压波形如图A11所示，仿真2 和仿真3 中各DG 输出电压的波形与仿真1 一致，仅存在检测时间的不同。

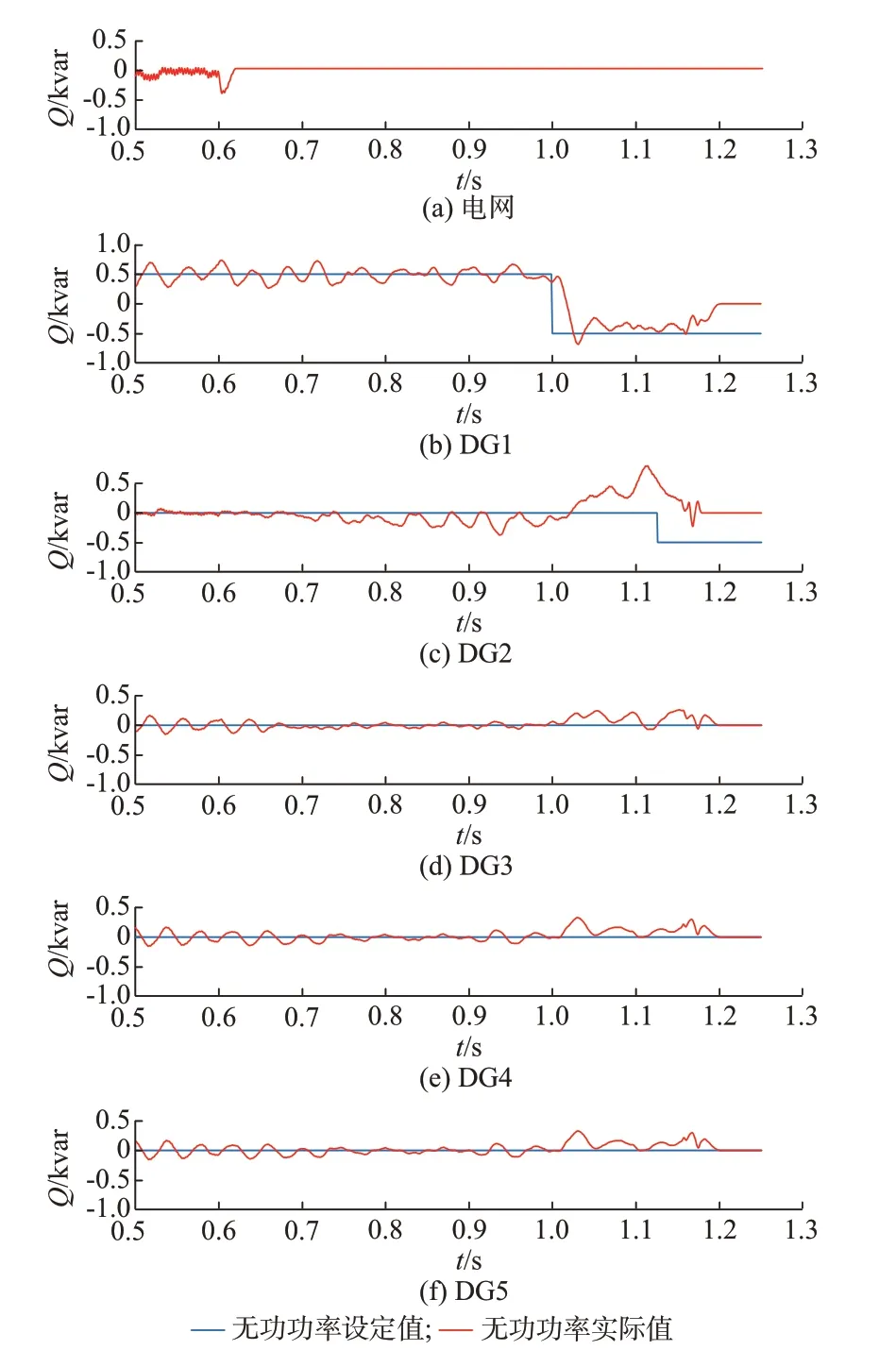
图5 电网与各DG 输出无功功率波形图（孤岛功率平衡）Fig.5 Output reactive power waveforms of power grid and each DG (with balanced island power)

由仿真数据可得仿真1 至3 中各逆变器的Qre；DG1 的Qref=ΔQref+Qdis，其中Qdis由式（7）进行计算，其他DG 的Qref为零，由ΔQ=Qref-Qre可计算各逆变器的ΔQ，不同负载性质下的仿真结果如表3所示。

3.2.3 仿真分析

通过对比分析无功功率扰动法和本文方法检测多DG 孤岛的仿真结果，可得出以下结论:

1）根据第1 章对稀释效应的分析，由3.2.1 节仿真结果可知，采用无功功率扰动法检测多DG 孤岛时，各DG 的ΔQ近似相等，即产生了稀释效应，导致孤岛检测失败。由表3 中本文方法的仿真结果，忽略控制系统的误差，可认为仿真1 至3 中DG1、DG3、DG4 和DG5 的ΔQ为零，即各从逆变器保持正常运行状态；而DG2 的|ΔQ|明显大于其他DG 的|ΔQ|，即孤岛所需或剩余的无功功率全部由DG2 提供或吸收，从而避免其他DG 共同输出或吸收无功功率，可有效地消除稀释效应，检测到多DG 孤岛效应。

表3 不同负载性质下的仿真结果Table 3 Simulation results with different load characteristics

2）由仿真1 中图5 可知，DG2 的|ΔQ|较大，使得ΔWQ快速增加并达到ΔWQset；由表3 中的仿真结果可知，DG2 在1.165 s 时检测到孤岛效应并切除，如附录A 图A11 所示，此时，孤岛的有功功率平衡被打破，因而其他DG 均可检测到孤岛效应。从逆变器最长切除时间为1.187 s，因此，孤岛检测时间为0.587 s（0.6 s 时发生孤岛效应）；仿真2 和仿真3 的孤岛检测原理与仿真1 相同，其孤岛检测时间分别为0.260 s 和0.230 s，即本文方法能够快速地检测到多DG 孤岛效应。

3）根据2.4 节可知，本文方法实现无盲区检测的条件是主逆变器可检测到|ΔQ|=0.5 kvar 的孤岛。仿 真1 至3 中DG2 的|ΔQ|分 别 为0.429、0.266、0.238 kvar，均小于0.5 kvar；由表3 可见，仿真1 至3均可成功检测到孤岛效应，因此，本文方法能够实现无盲区检测。

综上所述，对于多DG 孤岛检测，传统主动法存在明显的稀释效应，易导致孤岛检测失败，而本文通过控制主逆变器输出电压的频率来稳定孤岛频率，可以消除稀释效应，并在GB/T 33593—2017 标准［30］规定的2 s 范围内检测到孤岛效应。

4 结语

针对多DG 孤岛检测的稀释效应，本文根据孤岛无功功率平衡与频率的关系，提出了一种利用逆变器频率控制的孤岛检测方法。该方法利用定频率控制的主逆变器稳定孤岛频率，使得锁相环控制的从逆变器能够运行在正常状态，不参与主逆变器与负载的无功功率交换，从而消除了稀释效应，实现多DG 孤岛检测。本文方法依赖主逆变器的定频率控制，若主逆变器退出运行，如何将某台从逆变器转换为主逆变器是下一步研究的重点。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。