考虑交通网与配电网信息融合的台风后配电网抢修策略优化

郁 琛，李尚轩，谢云云，刘韶峰，常 康

（1. 南瑞集团有限公司（国网电力科学研究院有限公司），江苏省南京市 211106；2. 智能电网保护和运行控制国家重点实验室，江苏省南京市 211106；3. 国网浙江省电力有限公司桐乡供电公司，浙江省桐乡市 314500；4. 南京理工大学自动化学院，江苏省南京市 210094）

0 引言

由于配电网设计标准较低，台风灾害常会引起大量的配电网物理故障，导致用户供电长时间中断，造成经济损失［1］。2018 年，“玛莉亚”台风登陆中国福建省晋江市，导致当地供电线路受损严重，累计停电135 万户［2］；2015 年，超强台风“苏迪罗”登陆中国福建省莆田市，导致8.74 万个配电变压器（以下简称配变）台区停运、502.09 万用户停电，共造成约203 亿元的经济损失［3］。由于停电损失随停电时间而增加［4-5］，为减少停电造成的损失，需要制定配电网抢修策略，以减少故障停电时间。

目前，针对配电网灾后抢修调度已有大量研究。许多学者针对施工队调度［6-7］和物资调度［8-10］进行了研究。除了通过施工队和物资调度来减少抢修时间外，通过调整配电网的运行方式、配电网内的分布式电源（distributed generator，DG）和移动电源（mobile power source，MPS）构建孤岛供电等弹性运行方式同样能够减少停电时间［11-12］。文献［13］提出了一种配电网灾后动态抢修滚动优化方法，动态调整抢修队工作方案。文献［14-16］综合考虑了故障抢修和供电恢复的关联性，建立了含DG 的配电网多故障抢修与恢复协调优化模型。文献［17-18］提出了一个考虑DG 输出、网架重构和施工队调度的协调优化模型。文献［19］利用MPS 保证重要负荷供电，协调优化网架重构、施工队和MPS 调度。

上述研究未考虑道路交通对配电网抢修策略制定的影响。现有研究通常用简单的直线距离表示路程代价［20］。然而，台风灾害不仅会导致配电网故障，也会对道路交通造成损害［21］，进而影响人员物资调度方案。人员物资行驶路径和时间是抢修策略制定时的重要影响因素［22］，及时而准确的交通信息能够优化电网抢修策略，最大限度降低交通路况对于抢修决策的影响。随着电力系统信息采集能力的提升，现在的电力系统具备了接入交通信息的能力［23-24］。

近年来，关于交通网影响电网应急抢修与调度决策的研究已有学者进行了一定的探索。文献［25］提出了一种考虑动态交通网络的综合能源配电网灾后紧急响应策略，但文章只考虑了交通流量，未能体现灾害条件下道路受损情况。文献［26］对施工队和应急电源进行调度，提出了一种协同交通网和配电网的弹性提升策略，文中将交通网简化至仅包含道路长度和拓扑结构信息，而对于道路受灾损伤、拥堵等情况均未作考虑。文献［27］通过对灾害进行预测，使MPS 预先到达指定位置，也考虑了配电网和路网损伤、拥堵等场景，然而，文章仅在预规划MPS 存放点的过程中考虑交通信息，未能将其拓展至MPS 应急供电顺序的路径规划。

目前，配电网故障抢修研究中未能充分利用道路拥堵中断等非电气信息及适应外部交通环境的变化，在极端台风灾害频繁侵扰沿海电网且故障抢修策略已无法脱离复杂交通网单独制定的背景下，亟须开展关于交通网与配电网信息融合方法的研究，并在此基础上协调抢修与恢复手段，优化配电网灾后抢修策略。为此，本文提出了计及交通网与配电网信息融合的台风灾后配电网抢修策略优化方法。

1 基于交通网与配电网信息融合的配电网应急抢修框架

在电力系统具备了接入交通系统信息能力，产生相互作用、耦合关系的同时，相应的基于交通中断场景的灾后抢修与应急调度方法研究目前还不够完善。因此，本文提出了基于交通网与配电网信息融合的配电网应急抢修框架。

1.1 交通网与配电网信息融合框架

1）信息交互过程

交通网与配电网信息融合框架如图1 所示。交通网与配电网分属不同的公共事业系统，在抢修路径规划环节中，交通侧和电网侧分别采集并存储不同的数据类型。交通侧信息包含用于存储物资、配给MPS 和抢修队的仓库位置信息，影响人员物资通行能力和效率的道路限速、道路受灾拥堵和路口延误信息等。配电网可采集到故障点灾损位置信息、故障类型信息、故障点物资需求数量信息、仓库包含电力物资种类及储量信息、MPS 接入点信息。

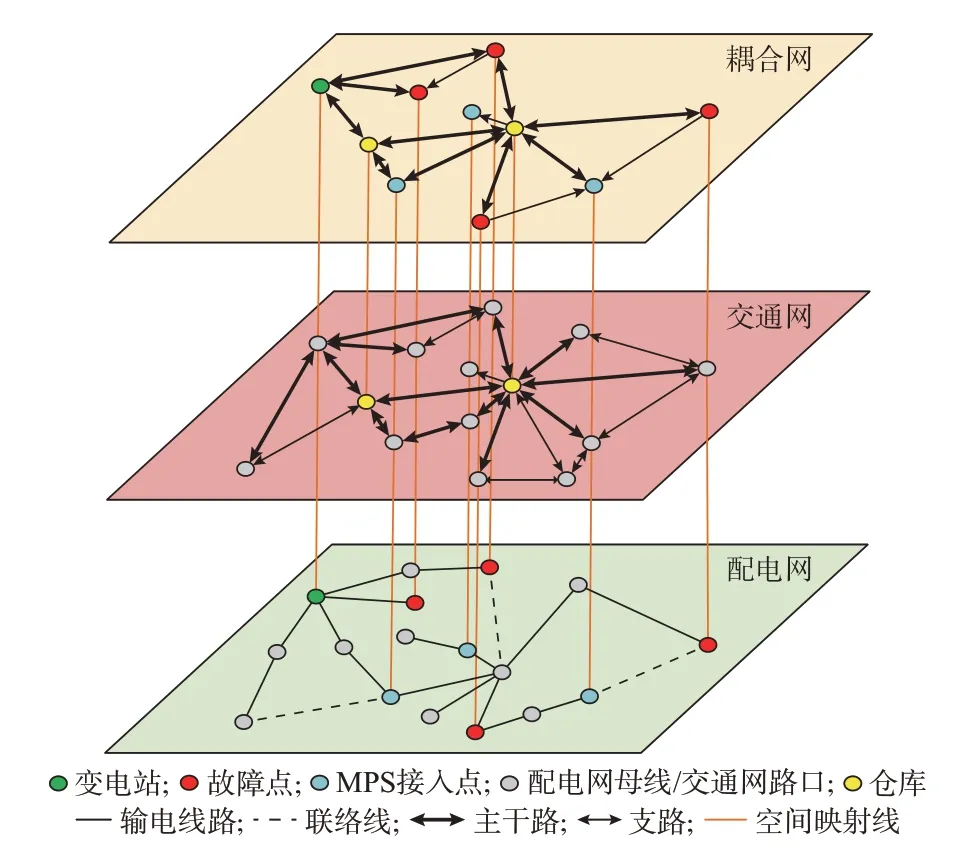
图1 交通网与配电网信息融合框架Fig.1 Framework of information integration between traffic network and distribution network

由于交通网的拓扑和道路通行状况会直接影响人员物资车辆的空间位置，而空间位置会影响当前配电网的抢修进程。因此，在考虑车辆的实际行驶路径和抢修时效问题的过程中，需结合电网与交通的现有数据资源，通过信息的交互与共享、数据的交叉与融合，实现决策量的全局优化。

基于此，根据路径规划需要，配电网对交通网映射路径规划所需的源宿节点以及主体信息；配电网接收以交通网为基础的抢修进程信息，确定当前抢修阶段下即任一故障点修复后的网架状态并安排相应的负荷恢复计划。在此基础上，应对规模庞大的交通拓扑进一步作简化处理，本文在交通网与配电网基础之上衍生出耦合网作为过渡阶段。

2）耦合网

耦合网本质上仍然是以交通网拓扑结构为基础，由交通网与配电网2 个单层复杂网络根据层间的映射联系构成，收集交通网与配电网关键耦合信息，并且将交通网与配电网在地理位置层面上共同包含的节点定义为耦合节点，用于描述两网之间的相互作用关系。耦合网中包含了由配电网提供的故障点和仓库等有待进行决策的节点以及由交通网反映的节点之间的路程长度等信息，通过一定的预先处理简化后续决策计算量。耦合网络层基于两网中提炼出的关键信息，其主要功能是应用数据挖掘、聚类分析，对仅具备单一层面的功能且不存在层间直接耦合关系的数据和节点进行清洗，剔除无用或冗余的信息，并进行数据聚合，为电网应急控制和调度提供数据支撑。

1.2 配电网应急抢修优化决策框架

考虑交通网与配电网信息融合的配电网应急抢修优化决策框架如图2 所示。耦合网收集两网在故障抢修过程中产生的存在耦合关系的地理信息，形成以交通拓扑为基础的初始网络，随后通过2 种措施进一步简化耦合网:1）去除耦合节点以外的交通拓扑节点，缩小耦合网的拓扑规模；2）采用聚类算法将故障点与仓库进行匹配，形成若干个小型簇，将后续的抢修优化模型求解场景相应缩小至单个簇的调度范围。

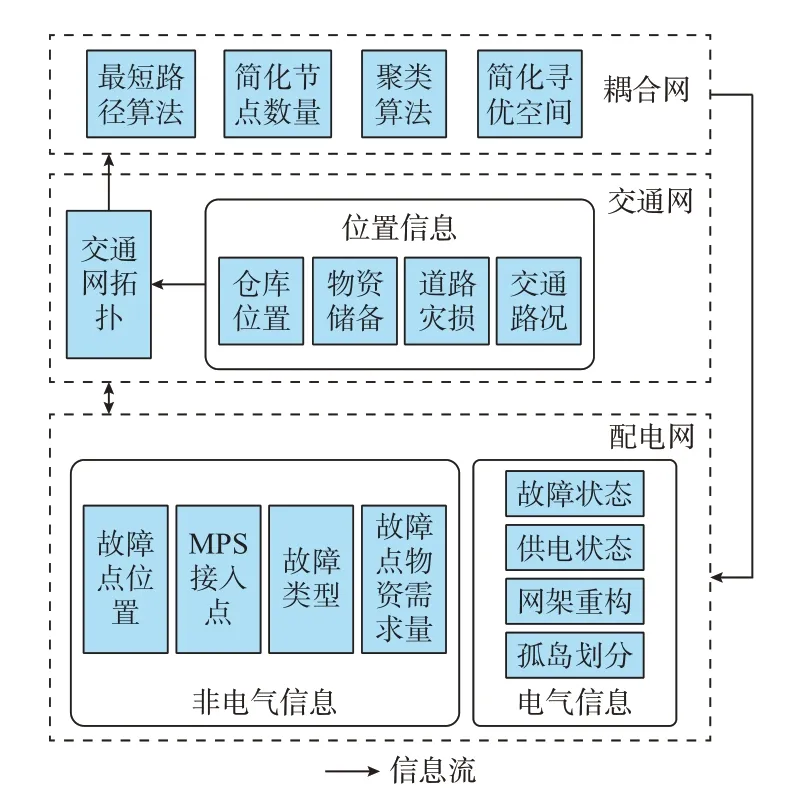
图2 优化框架与功能模块Fig.2 Optimization framework and function module

在此基础之上，故障点、仓库、MPS 接入点之间的最短路径已在耦合网的简化过程之中求得，并作为已知常量输入后续的故障抢修与负荷恢复决策模型进行求解。

2 交通网与配电网信息融合模型

本章针对配电网抢修策略制定过程中需要考虑交通网信息的问题，建立交通网与配电网信息融合模型。

2.1 台风灾害下的道路阻抗模型

为进一步量化路程时间作为道路权重或行驶成本，而非简单的定义道路长度和车速，本文引入美国联邦公路局（Bureau of Public Roads，BPR）路阻函数的概念作为时间衡量标准。

BPR 路阻函数模型对道路阻抗的性质与特点把握得相当准确，同时又因其数学性质良好，得到了广泛的应用［28］。其数学表达式为:

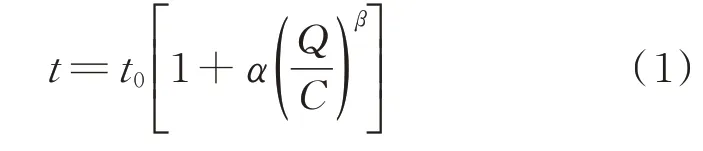
式中:t为车辆位于该道路的行驶时间；t0为道路的自由流行驶时间；Q为该道路的车流量；C为该道路的 实际通行能力；α和β为代标定参数，BPR 标定α=0.15，β=0.4。

台风灾害下交通路段会伴随积水、淹没和塌方等损坏，最终体现于道路通行能力的降低，修正后的BPR 路阻函数可表示为:

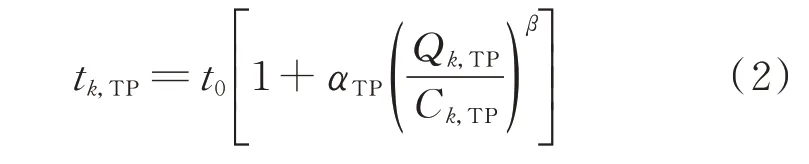
式中:tk，TP为台风灾害下道路k的车辆行驶时间，k∈K，其中K为道路集合；Ck，TP为台风灾害下道路k的通行能力；Qk，TP为该道路的车流量；αTP为参数。

当车辆抵达路口时，必然会受交通信号灯的阻滞影响。文献［29］提出了路口随机延误模型为:

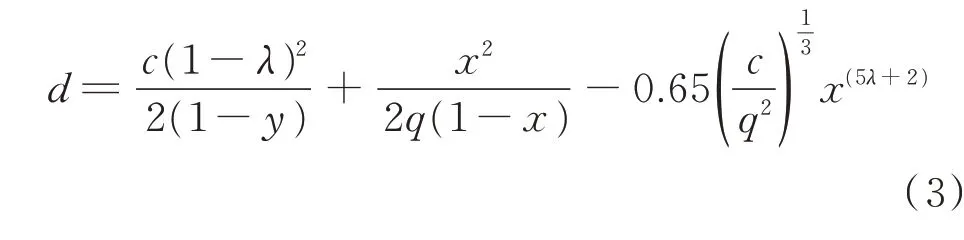
式中:d为进口道车辆平均延误时间；c为路口红绿灯信号周期；λ为路口交通灯的绿灯信号时长比（以下简称绿信比），若信号灯绿灯时长为g，则λ=g/c；q为实际进口道交通流量；y为进口道交通流量比，若进口道饱和流量S已知，则y=q/S；x为进口道饱和度，可表示为x=q/c=y/λ。

文献［30］给出了交通信号路口进口道延误计算公式为:

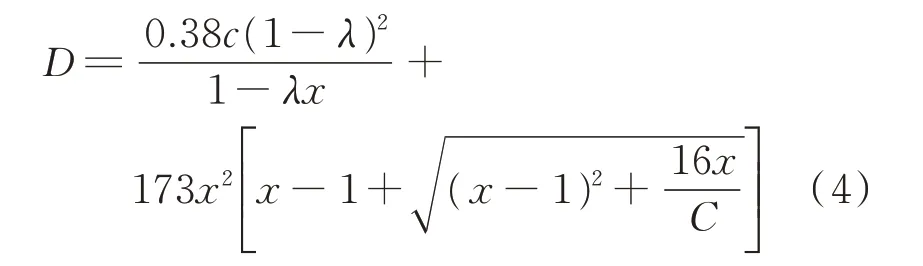
式中:D为路口进口道车辆平均延误时间。

Webster 公式将路口延误分为均匀延误、随机延误和修正延误3 个部分。当进口道饱和度很小的时候，后2 项之和占比较小，可忽略不计，但是随着饱和度的不断增大，其对计算结果的影响明显增大。美国道路通行能力手册（highway capacity manual，HCM）延误公式在综合考虑饱和度和车辆到达规律影响的前提下，将路口延误公式表达为标准延误和随机延误2 项延误之和，修正的模型计算结果更准确，该公式多被中国学者采用，其缺点是计算过程复杂且参数取值方法烦琐。因此，本文采用将Webster 延误公式和改进的HCM 延误公式相结合的形式表征台风灾害下的路口延误，最终得到的台风灾害下路口延误函数模型为:

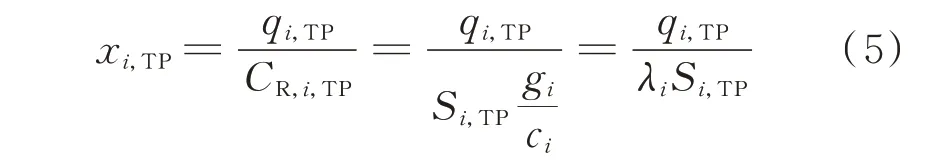
式中:xi，TP为台风灾害下路口i进口道饱和度，其中i∈I，I为路口集合；λi为路口i的 交通灯绿信比；qi，TP为台风灾害下路口i进口道实际交通流量；CR，i，TP为台风灾害下路口i进口道通行能力；Si，TP为台风灾害下路口i进口道的饱和流量；ci为路口i的交通灯信号周期时长；gi为路口i的交通灯的绿灯时长。

当xi，TP＜1 时，

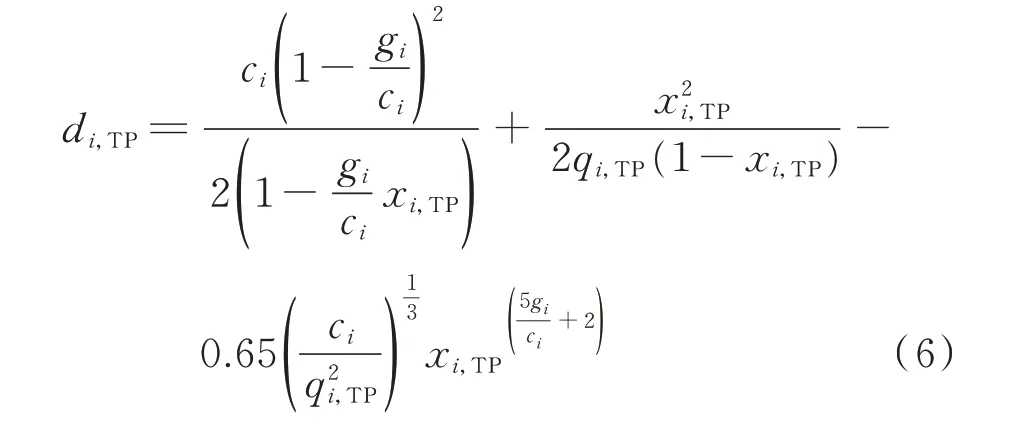
当xi，TP≥1 时，

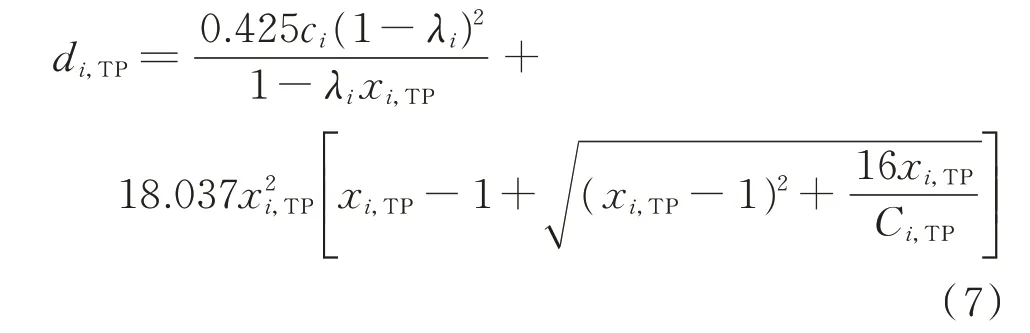
式中:di，TP为台风灾害下路口i的车辆平均延误时间。

综上所述，根据构建的台风灾害下的交通网路段行驶时间模型和交通灯信号路口延误模型，最后得到了台风灾害下的交通网道路阻抗函数，其数学表达式为:

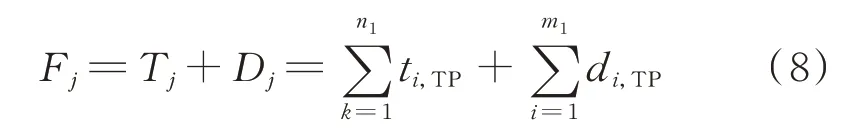
式中:Fj为台风灾害下路径j的阻抗值；Tj为路径j包含的n1个道路总行驶时间；Dj为路径j包含的m1个路口的总路口延误时间。

本文假设在台风灾害过后，配电网故障抢修所需的车流量远小于整个交通网中的车流量，且由于时间尺度短使其变化幅度较小，可认为在故障抢修持续时间内，交通网的车流量基本不发生变化，车辆在每条路径上的行驶时间由式（8）计算的道路阻抗所得作为道路权重，并保持数值上的恒定。

2.2 交通网拓扑简化

考虑到实际交通网规模庞大，本文采用了基于Floyd 算法的拓扑简化方法，原理如附录A 图A1 所示。故障点和MPS 接入点视为两网耦合节点，耦合节点和仓库均作为配电网中的关键节点并映射于交通网中，它们之间存在若干个道路节点。为减少后续优化问题的规模，本文使用Floyd 算法对任意2 个关键节点求解出最短路径，若两点之间无间接相连，则视为断开。

本文将车辆行驶时间和路口延误表征为路段的等效距离。相邻两点间的等效距离可表示为:

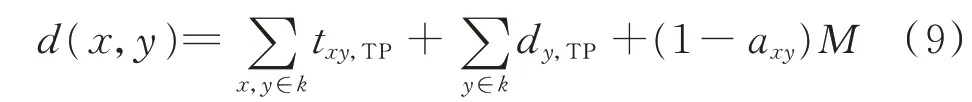
式中:d(x，y)为x、y间的等效距离；k为路段；引入0-1 变量αxy，从x到y连通为1，否则为0；txy，TP为台风灾害下道路xy的车辆行驶时间；M为无穷大常数，若x至y为单行道时，d(x，y)为无穷大。

为进一步提升计算速度，本文采用谱聚类将故障点分配给仓库。根据仓库数量，在路径规划之前将故障点划分成多个簇。

聚类过程如附录A 图A2 所示。聚类之后，同一簇只含有一个仓库和多个故障点，并且故障点只能被同簇中的施工队和物资车辆访问。

聚类模型为:

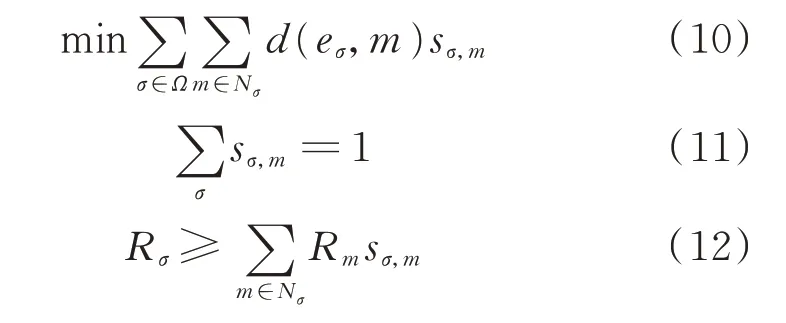
式中:Ω为所有簇的集合；Nσ为簇σ内故障点集合，m∈Nσ；d(eσ，m)为属于簇σ的仓库eσ与故障点m的距离；sσ，m为0-1 变量，故障点m分配给簇σ为1，否则为0；Rσ为簇σ内仓库物资储量；Rm为故障点m所需的物资量。

目标函数式（10）表示按最短等效距离将故障点分配给最近的仓库；式（11）表示一个故障点只分配给一个仓库；式（12）表示簇σ的仓库容量不小于簇内故障点的物资需求量。

3 考虑交通网影响的配电网抢修模型

配电网抢修涉及抢修施工队调度、配电网网架重构和配电网中DG 孤岛供电三者的协调，本章建立配电网抢修优化决策模型，实现配电网内供电负荷量最大化。

3.1 目标函数

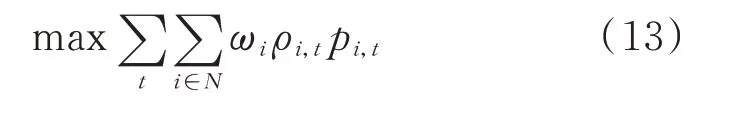
为尽可能地降低配电网故障引起的经济损失，本文以供电负荷量最大为优化目标，表达式为:式中:ωi为节点i的负荷权重；N为节点集合；ρi，t为节点i在t时刻是否连通的0-1 变量，若连通则值为1，否则为0；pi，t为节点i在t时刻所带有功负荷。

3.2 施工队调度约束

到达故障点的施工队在完成修复后也从该点离开，表达式为:

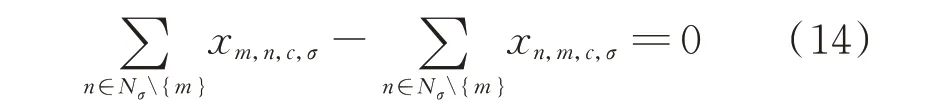
式 中:xm，n，c，σ为 簇σ内 施 工 队c从 故 障 点m移 动 到 故障点n的状态变量，若移动完成则值为1，否则为0。

施工队从仓库出发的表达式为:

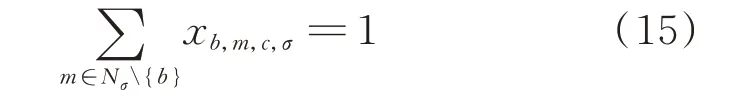
式 中:xb，m，c，σ簇σ内 施 工 队c从 仓 库b移 动 到 故 障 点m的状态变量，若移动完成则值为1，否则为0。

施工队最终返回仓库的表达式为:

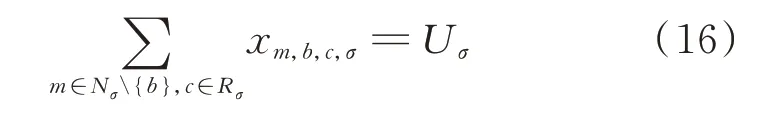
式中:Uσ为簇σ内拥有的施工队数量；Rσ为施工队集合。

任一故障点只能被一支队伍访问的表达式为:

式 中:ym，c，σ为 施 工 队c是 否 访 问 过 故 障 点m的 状 态变量，若访问过故障点则值为1，否则为0。

式（18）耦合了0-1 变量ym，c，σ和xm，n，c，σ，例如施工队c从故障点m到达故障点n，则施工队c必然访问过故障点m。

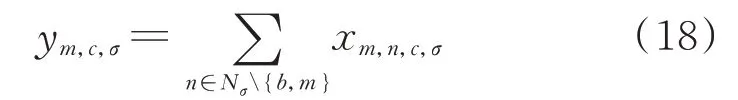
3.3 物资约束

物资约束形式上与施工队调度约束相近，具体推导过程见附录B 第B1 章。

3.4 故障修复时间约束

考虑到交通拥堵和道路受灾情况等交通网特性对故障恢复时间的影响，本节中的两点间的路程时间r均由式（8）所述的关键节点之间等效距离求得。

施工队抢修作业受故障点应急物资配送情况影响，本文假设任一故障点物资完全满足需求后，施工队才可进行抢修。

施工队到达的时间约束为:

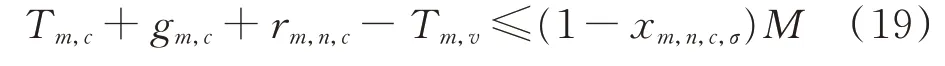
式 中:Tm，c和Tm，v分 别 为 施 工 队c和 运 输 车v到 达 故障 点m的 时 间；gm，c为 施 工 队c维 修 故 障 点m的 时间；rm，n，c为 施 工 队c从 故 障 点m移 动 到 故 障 点n的时间。

运输车到达时间约束为:

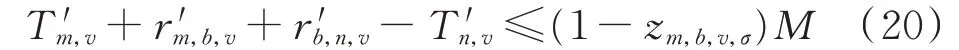
式中:T′m，v和T′n，v分别为运输车v到达故障点m和故障 点n的 时 间；zm，b，v，σ为 运 输 车v从 故 障 点m移 动 到仓库b的状态变量，若移动完成则值为1，否则为0；r′m，b，v为 运 输 车v从 故 障 点m移 动 到 仓 库b的 时 间；r′b，n，v为运输 车v从仓库b移动到故 障点n的时 间。

任一故障点只被修复一次，其表达式为:

式中:fm，t为故障点m在t时刻的修复状态，若已修复则值为1，否则为0。

施工队开始维修时间的表达式为:

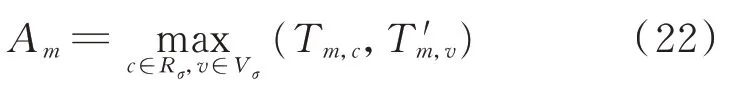
式中:Am为施工队开始维修时间；Vσ为运输车集合。

施工队完成维修的时间为:

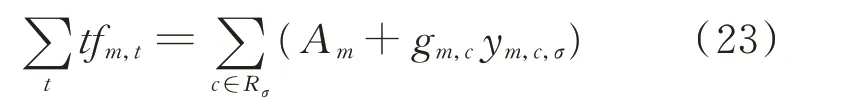
施工队开始维修的时间约束为:

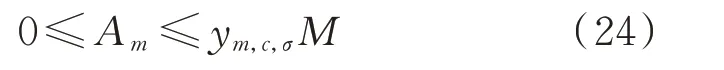
被修复的故障点将在接下来时间内状态都为可用，表达式为:

式中:zm，t为故障点m在t时刻的被修复状态，若已修复则值为1，否则为0。

当故障点状态未修复时，强制um，t为0 来耦合施工队与配电网约束，相关表达式为:

式中:um，t为故障点m在t时刻的可用状态，若可用则值为1，否则为0。

3.5 MPS 运行约束

当失电负荷尚未完全恢复时，宜采用DG 及MPS 配合的方式提高恢复效率。

MPS 调度约束与施工队调度约束相近，具体推导过程见附录B 第B2 章。

MPS 抵达下一个接入点n的时间为式（27）或式（28），即

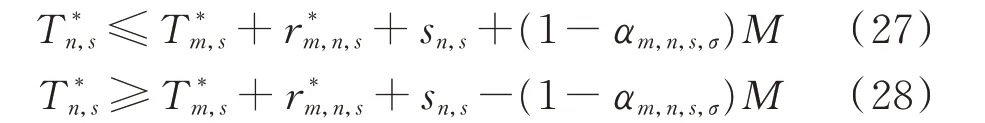
式 中:T*m，s和T*n，s分 别 为 第s个MPS 到 达 故 障 点m和n的 时 间；sn，s为 第s个MPS 位 于 故 障 点n的 持 续 供电 时 间；αm，n，s，σ为 第s个MPS 从 故 障 点m是 否 移 动至故障点n的状态变量，若是则值为1，否则为0。

MPS 抵达、离开时间约束:

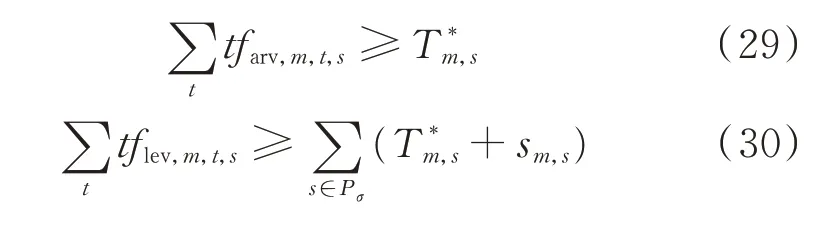
式 中:farv，m，t，s和flev，m，t，s分 别 为 发 电 车s在t时 刻 是 否到达和离开故障点m的状态变量，若是则值为1，否则为0；Pσ为发电车集合。

在MPS 供电持续时间内，该点的状态为:

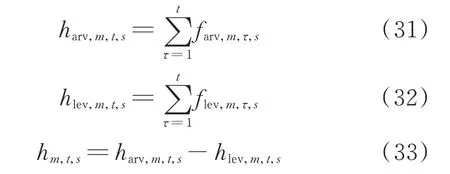
式 中:harv，m，t，s和hlev，m，t，s分 别 为 发 电 车 到 达 和 离 开 时其 位 于 该 点 的 可 用 状 态；hm，t，s为 供 电 持 续 时 间 内 的可用状态。

3.6 配电网约束

配电网约束具体推导过程见附录B 第B3 章。

4 求解方法

针对本文建立的配电网灾后故障抢修优化模型，其中非线性约束较多，难以直接采取数学方法进行求解，而智能算法可以直接求解含非线性约束的模型。在台风灾害发生后，需要进行一系列的抢修准备工作，包括:通过无人机对故障图像进行研判，确定故障类型及所需物资、临时建立应急物资仓库并调配所需物资入库等等，这些准备工作在获取到必要的信息之前直至抢修工作开始尚需一定过程，有相对比较充裕的时间计算抢修策略。另外，在故障抢修的过程中需要配合电网调度手段，有必要将抢修和调度问题分开采用智能算法求解来降低算法的编码维度。因此，本文所提模型采用分层智能算法求解。

上层模拟退火算法主要解决车辆路径搜索问题和人员物资调度策略；下层解决配电网网架重构和孤岛划分问题。具体两层算法总流程图如附录A图A3 所示，详细的上层求解流程及下层求解流程分别见附录A 图A4 和图A5。

5 算例仿真

5.1 算例场景

本文以IEEE 69 节点标准系统为例。该配电网有69 个节点，额定电压为12.66 kV，5 个联络开关，电压偏差范围为±5%。此外，DG1 与DG2 分别安装于节点33 和65 处，其容量均为800 kW。失电负荷的负荷等级如附录C 表C1 所示，一级、二级、三级负荷权重系数分别为100、10、1。

台风灾害发生后，交通网与配电网同时受到影响，如图3 所示。配电网中F1～F10处线路发生故障。交通网中节点17 和18 之间道路损坏，无法通行，同时道路对应车速有所降低，道路网中节点12 和17为应急仓库位置，共有4 个施工队（repair crews，RC）、2 辆MPS 以及6 辆物资运输车参与抢修。假设不同故障类型的预计抢修时间已知。

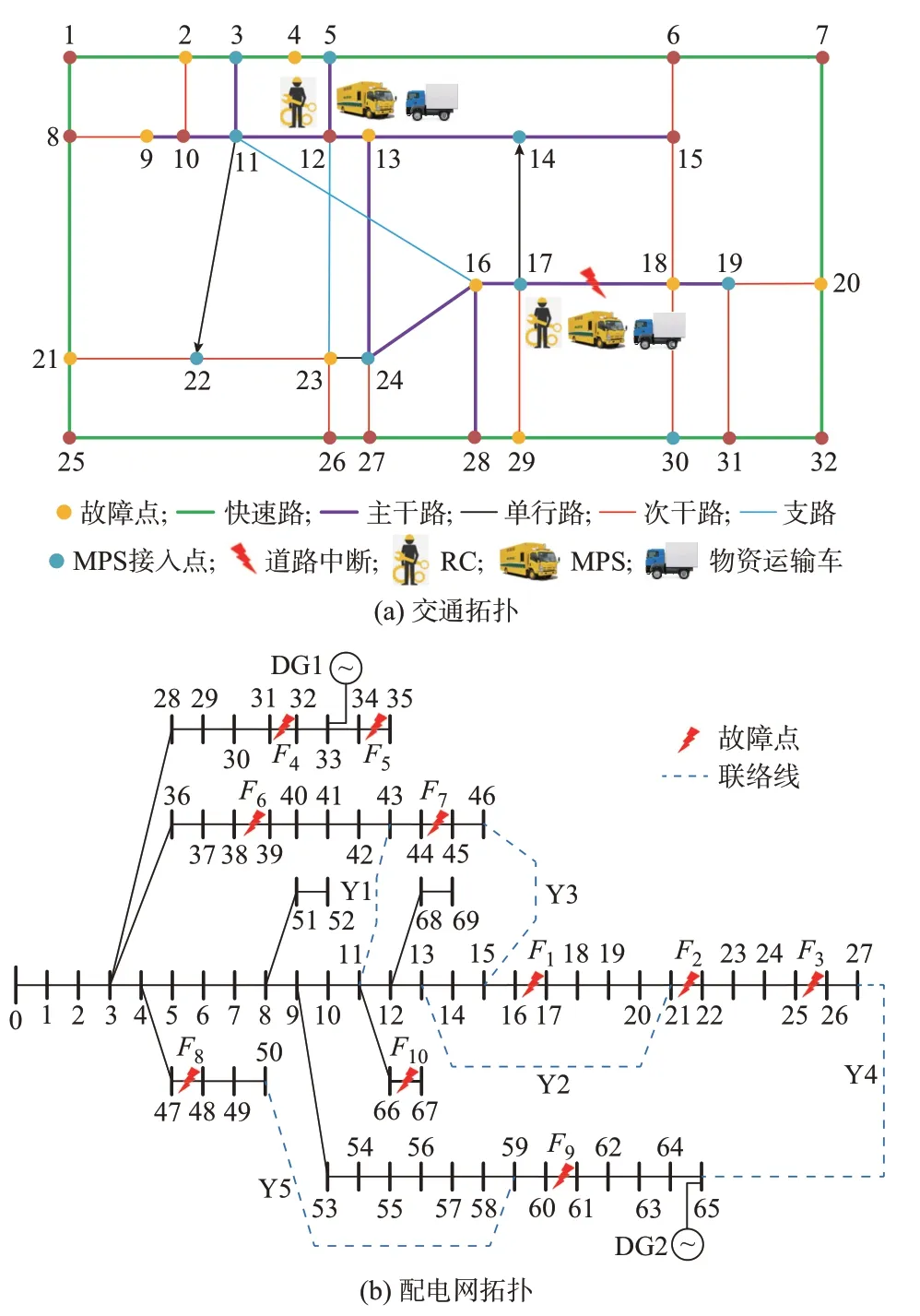
图3 交通网与配电网拓扑Fig.3 Topology of distribution network and traffic network

5.2 抢修调度优化方案

采用本文提出的考虑网架重构与孤岛划分的灾后配电网抢修策略可以缩短用户停电损失，最终得到的抢修调度方案如表1 所示。其中，Trans（1，F6）表示施工队1 号于0 时刻出发前往故障点F6，C（Y1）表示该时刻联络线Y1 闭合，O（Y2）表示联络线Y2 断开，Repaired（4，F2）表示在273 min 时故障点F2被施工队4 号所修复，MPS2（23/182）表示编号为2 的MPS 于该时段接入23 节点，并持续供电182 min。各调度单位工作情况如附录C 图C1、图C2 和图C3 所示，直观表现了其在各个时段的工作状态。算法经过11 次迭代耗时36 min 后目标函数收敛达到最优。

表1 考虑交通网影响的调度方案Table 1 Dispatch scheme considering effect of traffic network

5.3 对比分析

1）抢修策略对比

考虑DG 与MPS 对台风后配电网多故障抢修的影响，为了体现其存在价值，将所提策略与不含DG 与MPS 的抢修策略负荷恢复曲线对比，得到的仿真结果如图4 所示。其中，方法1 考虑了抢修和物资；方法2 考虑了抢修、物资和网架重构；方法3 考虑了抢修、物资、网架重构和DG；本文方法考虑了抢修、物资、网架重构、DG 和MPS。

由图4 可知，在配电网发生多故障时，仅考虑故障抢修的策略复电时间间隔长，负荷损失量大，当联络线与DG 参与恢复后，能明显提升故障初期负荷恢复量，进一步地，MPS 参与调度后，能在初期阶段为重要用户供电，减少社会经济损失，并提高了抢修恢复效率。

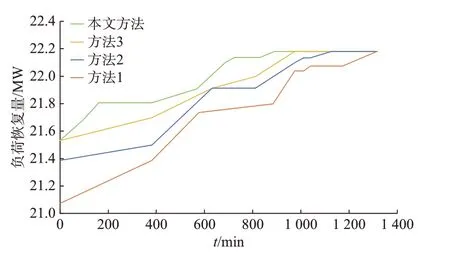
图4 不同抢修资源下的负荷恢复曲线对比Fig.4 Comparison of load recovery curves with different rush repair resources

2）交通网影响对比

为体现交通网信息融合后对于台风后配电网多故障抢修的影响，本文分别对比了考虑交通网和不考虑交通网时的抢修策略，并给出了对比算例，仿真结果如图5 所示。

由图5 可知，在台风后发生配电网多故障时，仅考虑道路长度和车速得到的抢修方案负荷恢复效率更高，而考虑灾后交通网中断和通行能力等影响得出的抢修方案则更为保守，后者在实际抢修过程中更具有可行性。

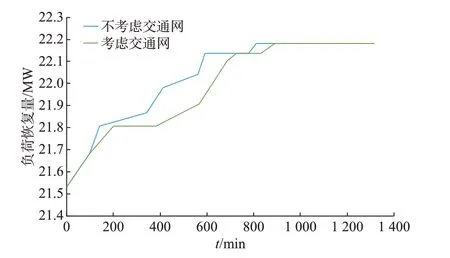
图5 交通网影响下的负荷恢复曲线对比Fig.5 Comparison of load recovery curves with effect of traffic network

表2 为不考虑交通网影响下的抢修调度方案。

表2 不考虑交通网影响下的调度方案Table 2 Dispatch scheme without considering effect of traffic network

由表2 可知，在未考虑交通网影响的前提下，t=0 时，抢修队4 被派往故障点F2。在192 min 时，该故障点被修复。然而，台风灾害发生后，路段17和18 因中断无法通行，由于仓库位置分布，仍然由距离较近的抢修队4 对故障点F2进行抢修，但修复时间会延后至273 min，这在现实中是更为合理的。此外，考虑交通网影响的抢修策略和不考虑其影响得到的策略在时间和安排上不完全相同，在实际操作上，后者因通行问题在调整方案时将更加困难。因此，在灾后配电网故障抢修过程中考虑交通网因素虽然牺牲了一定程度的负荷恢复效率，但是在实际工程实践上是有必要的。

6 结语

由于现有配电网故障抢修的研究未能充分考虑交通路况和道路受灾中断对抢修资源调度的影响，本文建立了计及交通网与配电网信息融合的灾后配电网应急抢修策略优化模型。该模型通过构建交通网与配电网信息融合框架，并引入网架重构与孤岛划分协同故障抢修进行策略优化，实现了负荷恢复效率的提升。进一步地，在恢复过程中引入MPS 动态调度，有效保障了大面积停电情况下重要电力用户的供给。仿真结果表明，本文方法能够计及交通网对配电网恢复的影响，有助于提升配电网恢复的效率。

后续研究将会致力于建立考虑多种不确定性的台风后配电网抢修恢复策略模型，使其能够考虑本文研究中所忽略的约束，进一步提高本文优化模型的精度。此外，对于应急决策的快速性要求，后续将会进一步对模型进行线性化，采用分布式算法提升紧急情况下的计算效率。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。