考虑桩土作用的桥墩车撞动力响应分析

岳凯乐，吉喆，张世蒙，王贵春

(1.郑州大学 土木工程学院，河南 郑州 450001；2.荥阳市交通运输局，河南 郑州 450100)

近年来，我国交通事业迅速发展，已建桥梁数量与日俱增。各种原因引起的车辆撞击桥墩的事件也时有发生。因此深入研究桥梁结构受撞后的动力响应具有理论和现实意义。车辆撞击桥梁往往发生在桥墩部位[1]，因此，本文主要研究桥墩受车辆撞击的动力响应。近年来，很多学者对该课题进行研究，并取得了显著成果。曹伟等[2]分析了用8 t双轴卡车以不同速度撞击桥墩的损伤情况，提出了桥墩防撞加固方案。赵武超等[3-4]以38 t重型货车作为撞击车辆，研究了桥墩直径、轴压比、箍筋间距、车辆偏心距与车辆货物刚度对桥墩受撞击后动力响应的影响，得到桥墩的破坏模式与撞击力，并与由规范计算的结果进行了比较分析[5-6]。陈林等[7]分析了4种边界条件的桥墩受撞击后的动力响应，结论为分析中是否考虑上部结构的约束作用对桥墩的动力响应有显著影响，且箍筋配筋率也对桥墩抗撞击能力有很大作用。李瑞文等[8]建立了双柱式桥墩模型，其截面为长方形，以撞击车辆质量与速度为控制变量，计算了40种工况下的车辆撞击力，拟合了撞击力经验公式和半正弦荷载曲线。王娟等[9]建立了典型的双柱式圆形截面桥墩模型，考虑了上部结构的影响，设桥墩底面为固结约束，分析了桥墩受车辆撞击的动力响应，并将计算结果与SHARMA等[10]分析的情况进行了对比，将桥墩的破坏形态进行了定量分类。CAO等[11-12]建立了2种截面形式的混凝土单墩模型，以12 t的满载F800双轴卡车作为撞击车辆，以路面坡度、车辆偏心距和卡车货物刚度为研究参数，计算得到了F800卡车的名义撞击高度，认为卡车撞击力峰值与卡车重量之间并没有必然的联系。以36 t半挂车作为撞击车辆，设桥墩顶部与底部为固定约束，以撞击速度及桥墩箍筋配筋率为变量，分析了桥墩受车辆撞击的动力响应，并与美国规范AASHTO(2017)LRFD的计算结果进行了比较。ABDELKARΙM等[12]建立了考虑桩土作用的单墩模型，以桥墩参数为变量，利用敏感性分析方法，提出了等效撞击力的计算公式。上述文献均对桥墩受撞击后的动力响应及损伤进行了探讨，但其桥墩边界多为固端边界或者只是简单考虑桩土作用，并未对采用各桩土模型计算的桥墩动力响应进行比较。文献[12]将圆柱桥墩在地面以下1 m处进行固结，结果表明与直接在地面处固结的情况相比，其受撞击位置侧向位移增大且出现明显的弯曲破坏，故桩土作用不可忽略。本文利用ANSYS/LS-DYNA软件，建立5种考虑桩土作用的模型。同时为了便于比较，也建立了未考虑桩土作用的墩底固结模型，以车辆撞击速度作为控制变量，分析了桥墩受撞后动力响应与损伤特征。

1 有限元模型与验证

1.1 车辆与桥梁参数

以郑州四环线某桥梁为背景，建立有限元分析模型。主梁单跨长度为30 m，桥墩为双柱式，其直径为1.4 m，基础采用直径为1.5 m的钻孔灌注桩，上部结构由5片预应力混凝土T型简支梁构成。

车辆模型选用美国NCAC研发设计的福特F800双轴卡车，如图1所示。该模型广泛应用于碰撞研究领域[1-3,7,12]，车辆的长×宽×高为8.58 m×2.44 m×3.32 m，车厢货物材料模型为*MAT_ELASTΙC并采用实体单元建模。通过附加密度法控制整车质量，设置车辆总重为8 t，撞击行驶速度分别为60，80和100 km/h。

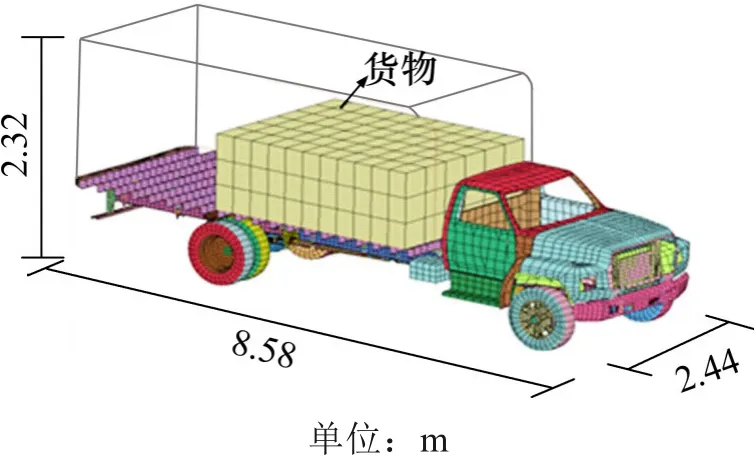
图1 车辆模型Fig.1 Model of vehicle

桥梁有限元模型如图2所示，其中支座与垫石和主梁的接触均采用LS-DYNA中的ASTS算法，忽略动静摩擦差异，上述2个接触面摩擦因数分别为0.3和0.06[13]。利用关键字*LOAD_BODY_Z考虑全局重力作用，不同方法所建立的桥梁模型差异较大，6种桥梁模型单元数量在135 000至283 000个之间。车辆对桥墩进行横桥向撞击。

图2 桥梁模型Fig.2 Model of bridge

1.2 桩土模型与墩底固结模型

1.2.1 等效嵌固法模型

等效嵌固法是数值模拟桩土作用的常用方法[14]，常采用3倍、5倍和8倍桩径长度约束，即将桩基在局部冲刷线或淤泥以下深度为3倍、5倍和8倍桩径处设置固结约束，此时3倍、5倍及8倍模型的桩长分别为4.5，7.5和12 m。

1.2.2 等效弹簧法模型

《公路桥涵地基与基础设计规范》中的m法是计算桩土作用常用的方法[15]，m为地基水平向抗力系数的比例系数。通过在桩基周围等距建立离散弹簧单元模拟土壤对桩的支撑作用，弹簧本构选择MATS08，仅考虑弹簧单元的压缩响应而不考虑其拉伸响应。各层弹簧刚度Ki由式(1)计算。

式中：m可通过查阅规范(JTG 3363—2019)合理选用；b0为桩基有效计算宽度；z为桩基单元划分高度。

1.2.3 有限域土体模型

有限域土体法是一种考虑桩土作用更为精准的方法。但由于土体体积庞大、计算收敛困难，仅在桩基周围一定范围内建立土体模型。土体水平方向为一矩形，各边距桩周均为1 m，竖直方向土体尺寸为21 m[17]。

1.2.4 墩底固结模型

为便于与上述桩土模型进行比较，建立不考虑桩土作用的墩底固结模型，即将桥墩底端固结。

1.3 单元与接触

采用SOLΙD164单元建立桥墩模型，通过增加混凝土弹性模量考虑钢筋对桥墩刚度的贡献[18]。桥墩单元尺寸控制在50 mm×50 mm左右[19]。考虑到计算耗时，有限域模型的土体单元网格尺寸控制在300 mm×300 mm。

1.4 材料本构

选用MAT159[20]作为混凝土本构，该模型对混凝土桥墩受撞击后的动力响应有很好的模拟效果[21]，考虑混凝土应变率效应。MAT005[20]作为土体本构，其屈服极限函数φ由式(2)计算。

式中：J2=Sij Sij/2，为应力偏量第二不变量；a0，a1和a2为常数；P为压力。

1.5 碰撞有效性验证

为验证上述材料本构和接触关系的准确性，建立与文献[21]落锤试验相对应的有限元模型。试验装置如图3所示，其中梁截面尺寸为250 mm×150 mm，长度为1 700 mm，混凝土抗压强度为42 MPa，最大骨料尺寸为10 mm，钢筋屈服强度为426 MPa。限制梁体的平面外位移，使400 kg的落锤从距离梁上部1.2 m处自由落体对梁产生冲击作用。由图4和图5可以看出，模拟得到的碰撞力及梁跨中挠度时程曲线与试验结果具有很好的吻合度。图6所示为梁受到冲击后的最终损伤特征与落锤试验结果的对比，可以看到两者的剪切破坏与受压破坏特征相吻合。这说明本文采用的混凝土本构及接触算法是有效的。

图3 落锤试验装置Fig.3 Drop hammer test setup

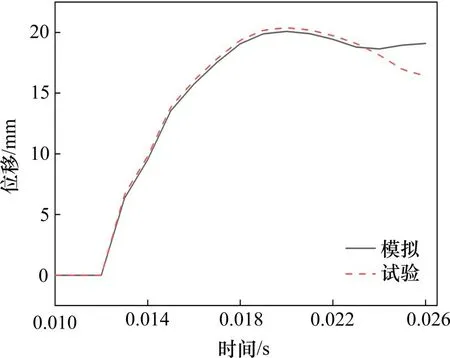
图4 梁跨中节点挠度时程曲线Fig.4 Time-history curves of def lection at midspan

图5 撞击力时程曲线Fig.5 Time-history curves of impact force

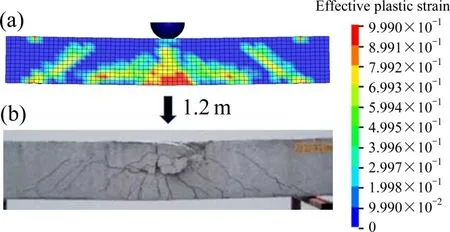
图6 梁受冲击荷载后的损伤对比Fig.6 Damage comparison of beam after impact

2 桥墩动力响应分析

2.1 撞击力分析

图7 为撞击速度为60，80及100 km/h时各模型的撞击力时程曲线。3种速度下，采用3倍模型，撞击力峰值最大，分别为2.41，5.13和8.25 MN，采用未考虑桩土作用的固结模型所得撞击力峰值最小，分别为2.28，4.52和7.04 MN。各桩土模型计算所得撞击力持时范围分别为0.23～0.26 s，0.21～0.23 s和0.18～0.19 s，易知撞击力持时随着车速增加而减小，其中固结法持时分别为0.26，0.23和0.19 s，均大于桩土模型时撞击力持时。每种车速下采用3倍、5倍和8倍模型所得撞击力峰值依次递减。采用弹簧法和有限域法所得撞击力峰值位于固结法与8倍模型的情况之间。

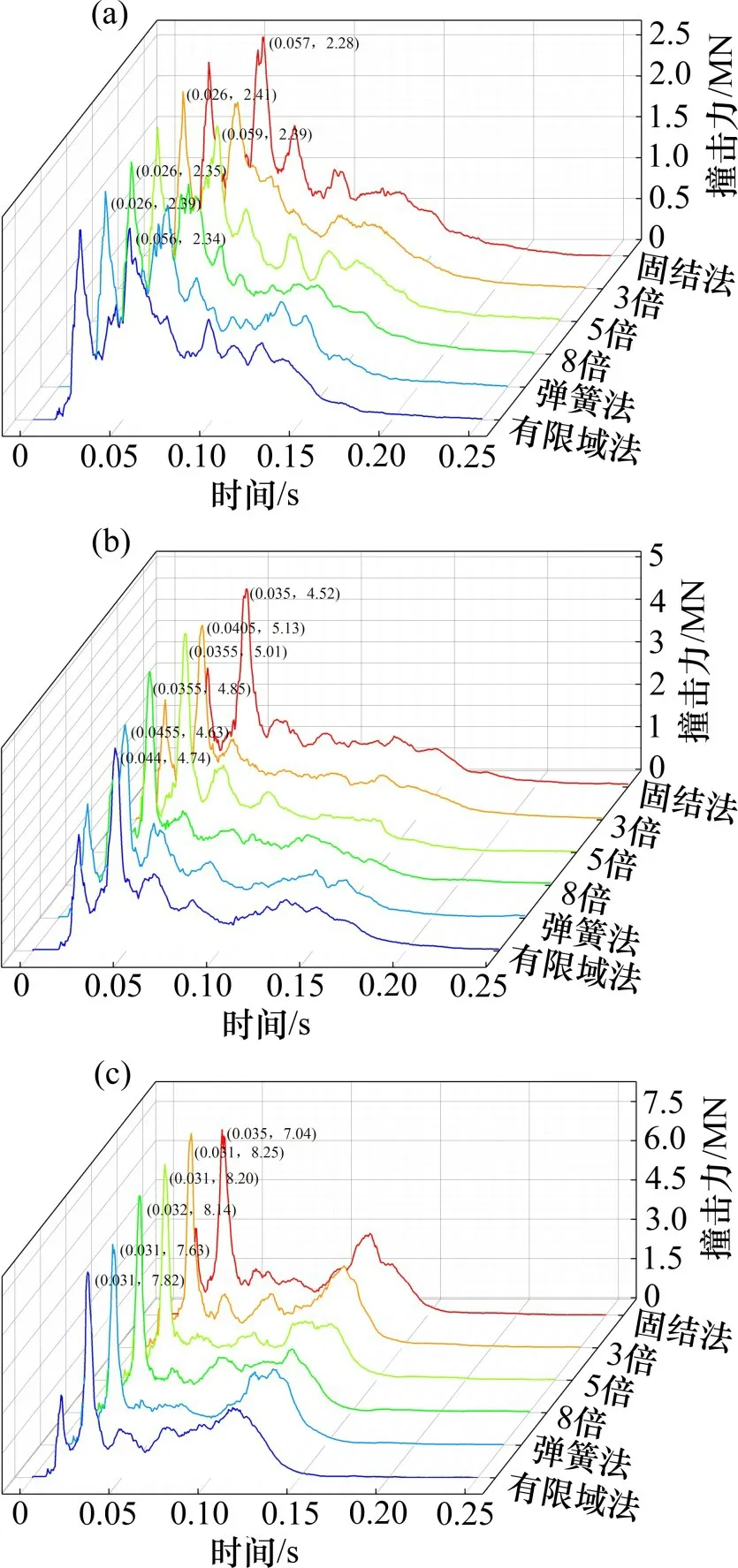
图7 撞击力时程曲线Fig.7 Time-history curves of impact force

图8 为用各模型计算所得车头在撞击方向位移时程曲线。可以看到，用各桩土模型计算所得车头位移峰值差异不大，这说明车头变形对用各桩土模型得到撞击力具有相同程度的影响。而用固结模型所得车头变形最为严重，其最大位移值为880 mm。这是由于固结模型是将桥墩底部固结，所以其桥墩刚度相比桩土模型的桥墩刚度更大，此时车辆与桥墩的撞击相当于车辆与刚性墙的撞击，因此由车头变形消耗的动能相比桩土模型的情况要更多，故其对应的撞击力峰值也会相应减小。

图8 车头位移时程曲线Fig.8 Time-history curves of vehicle front displacements

JTG D60—2015采用等效静力法规定城市桥墩抗车辆撞击荷载限值为1 000 kN[5]，如表1所示，利用式(3)将3种车速下各模型得到的撞击力时程转化为等效静力。可以看到，3种车速下采用各模型计算所得撞击力峰值(PDF)和等效静力值(ESF)分别约为规范限值的2.4倍、4.8倍、7.8倍和0.7倍、0.9倍和1.3倍。相比于撞击力峰值，各模型所得等效静力值差异较小，当车速超过100 km/h时，我国规范规定的1 000 kN限值偏小，而美国AASHTO[6]规范规定撞击力限值为2 700 kN，较为保守。

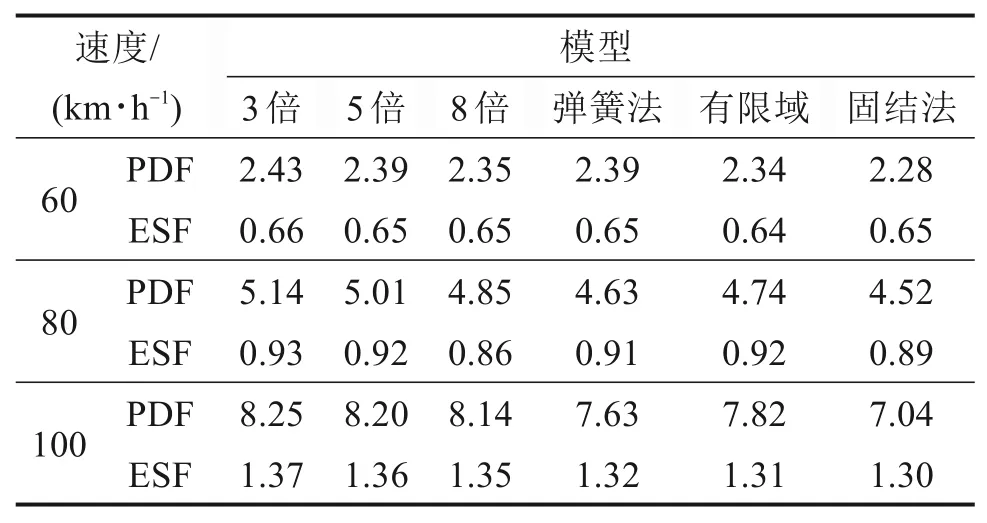
表1 撞击荷载与等效撞击力Table 1 Ιmpact forces and equivalent static forces MN

式中：Fmean为等效撞击力；I为撞击力冲量，其计算式为为撞击力与时间的函数；T为撞击力持时。

图9 和10所示分别是速度为80 km/h时，由5倍模型得到的车辆发动机及车厢货物速度时程曲线与撞击力时程曲线，图11为撞击过程示意图。观察图9～11，可将整个车桥碰撞过程划分为3个阶段：

图9 发动机与货物速度时程曲线Fig.9 Time history curves of engine and cargo speed

图11 车辆撞击桥墩过程Fig.11 Process of vehicle-pier collision

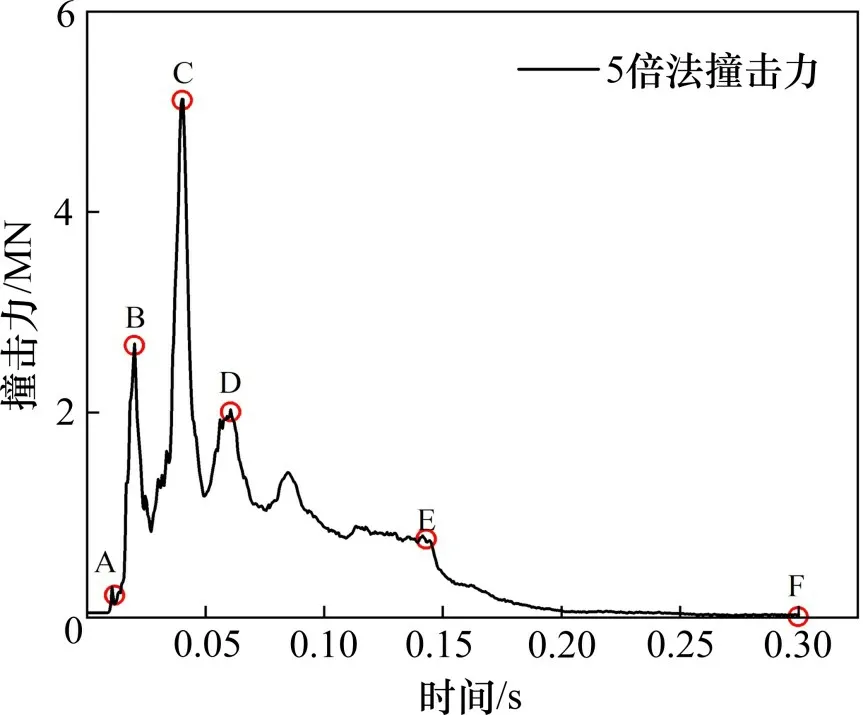
图10 撞击力时程曲线Fig.10 Time-history curves of impact force

第1阶段为撞击力产生阶段，即车辆与桥墩初始接触时的情况。t=0.02 s时，发动机速度与货物速度分别为22.22 m/s和21.7 m/s，两者相差较小，此时撞击力保持较低水平，车头出现轻微变形。

第2阶段为撞击力上升阶段。由于发动机与桥墩发生碰撞，撞击力迅速增加至峰值，在0.04 s时，发动机速度降至2.29 m/s，相比第1阶段的情况，下降幅度为89.7%，而货物速度为21.2 m/s，仅下降0.2%。

第3阶段为撞击力稳定阶段。即撞击力存在局部峰值，总体上处于平稳减小状态，此时车头已经出现明显压溃变形。在0.06 s时，发动机速度为0.569 m/s，相比第2阶段下降的情况，下降幅度为75.2%，货物速度为17.9 m/s，仅下降15.6%。说明此时车厢货物因惯性仍保持较高速度，而车头部分即将停止运动，因此第3阶段撞击力主要由货物的二次挤压产生。由图7(c)可以看到，车速100 km/h时，由车厢货物产生的二次挤压碰撞力明显增大。t=0.23 s时，撞击力减至0 MN，发动机与货物速度分别为-0.524 m/s和-0.677 m/s，表明车辆向反方向运动，撞击过程基本结束。

2.2 桥墩位移分析

图12 为3种速度下桥墩顶部横桥向位移时程曲线。由图12可知，桥墩变形特征为先沿着车辆撞击方向发生显著位移并达到峰值，然后随着车辆回弹，桥墩弹性变形恢复，剩余塑性变形。这一特征与文献[13]中进行的RC墩柱撞击试验所得位移变化特征具有相似性。

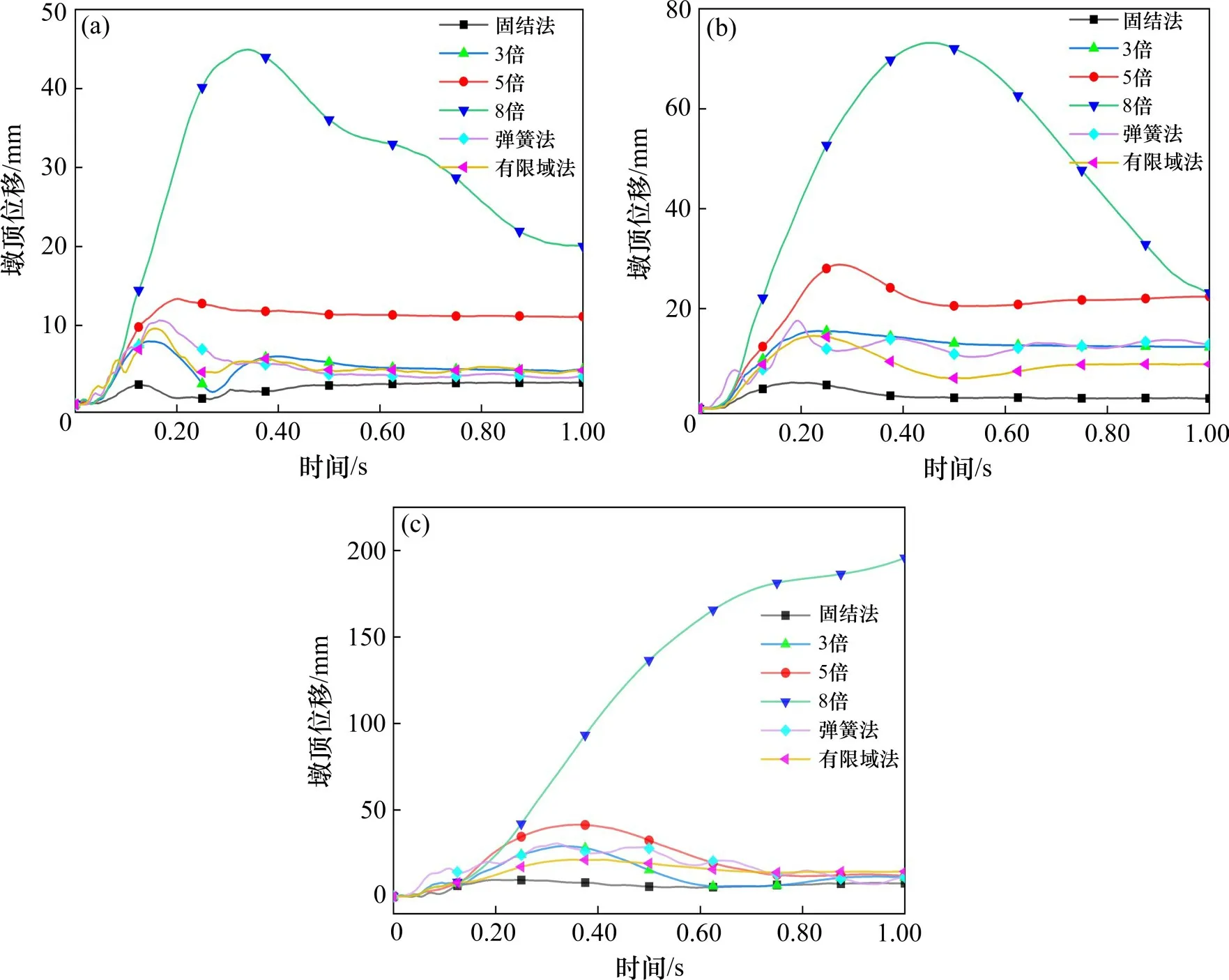
图12 位移时程曲线Fig.12 Time-history curves of displacements

就横桥向位移而言，3种车速下由固结法得到的位移峰值分别为2.47，5.19和9.55 mm，其值均小于由桩土模型的情况，而由8倍模型得到的位移值分别为44.9，77.4和194 mm，约分别为前者的18倍、15倍和20倍。当速度为100 km/h时，8倍模型桥墩发生垮塌，故位移峰值194 mm取自撞击发生后0.15 s时刻对应的值。同时看到由3倍、5倍和8倍模型得到的位移依次增大，其中由8倍与3倍模型得到的位移值最大相差164.9 mm，可见桩基固结深度越大的桥墩其刚度越小，故受撞击后的响应也会越明显。另外，用3倍模型、弹簧法和有限域法所得位移峰值差异较小，峰值最大相差9.3 mm，说明此3种方法对本工程具有相近的模拟效果。

2.3 桥墩损伤特征分析

图13 所示为等效嵌固模型受车辆撞击的损伤状态及发生损伤的对应时刻。图13(a)中车辆与桥墩初始接触阶段，桥墩受撞位置出现局部受压损伤。图13(b)中桥墩损伤范围逐步扩大，撞击位置背面出现受拉损伤。查看此处单元应力可知，该区域混凝土主要是发生弯曲拉应力导致的破坏。图13(c)中桥墩与盖梁、桩基与系梁连接部位及桩基嵌固端均出现不同程度损伤，且被撞桥墩出现了明显的剪切损伤面，即冲剪破坏效应[24]。图13(d)为撞击作用消失时桥墩的损伤状态，由1.3节知，由于用8倍法所得墩顶位移过大，其盖梁中部也出现一定程度损伤。另外，用3倍、5倍和8倍嵌固模型出现相同的损伤特征所需时间依次增加，这是由于当桩基嵌固深度越大，桥墩就表现的越“柔”，其受到横向冲击作用时的响应时间就会越长，反之则亦然。

图13 桥墩不同时刻损伤状态Fig.13 Pier damage status at different times

由上述内容可知，桥墩受撞后的损伤部位主要是各构件连接处。为方便描述，定义横桥向桥墩与桩基连接部位为撞击特征点。图14为撞击速度为80 km/h时各桩土模型所得撞击特征点Von Mises应力时程曲线。可以看到，由3倍、5倍和8倍模型所得撞击特征点应力峰值依次增大，其值分别为3.41，4.72和5.59 MPa，而弹簧法与有限域法所得应力峰值分别为3.22 MPa和2.41 MPa，其值均小于等效嵌固法的情况，由8倍模型所得应力值峰值分别约为后两者的1.7倍和2.3倍。产生这种差异的原因在于弹簧法与有限域法的桩基周围设置了约束条件，而等效嵌固法仅在桩基底端设置固结约束，因此由嵌固法所得应力峰值偏大。这说明，使用不同桩土模型所得撞击特征点应力值的差异与桩周的边界条件设置关系密切，因此在进行桥墩受撞的应力分析时，使用弹簧法与有限域法所得结果更为准确。

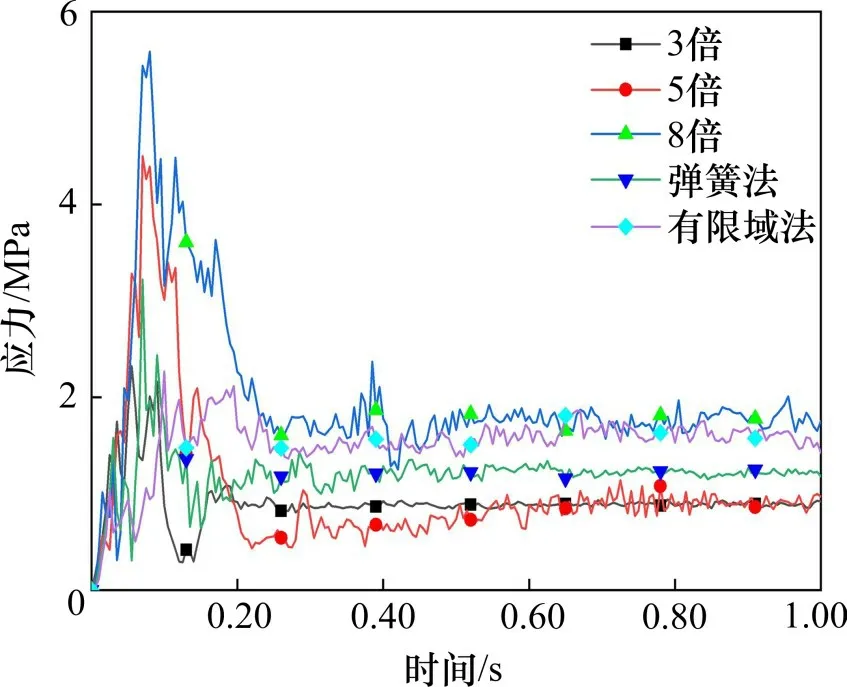
图14 应力时程曲线Fig.14 Time-history curves of stress

3 结论

1)未考虑桩土作用的固结模型所得撞击力峰值比桩土模型的情况偏小，其对应的撞击力持时较长，车头部分变形偏大。3种速度下采用8倍模型、弹簧法和有限域法所得撞击力峰值差异较小。另外，撞击力分布与车辆内部构造直接相关，撞击力峰值主要由发动机碰撞产生。

2)关于桥墩横桥向位移，固结法所得位移值均小于桩土模型的情况。等效嵌固法桩基嵌固深度直接影响桥墩刚度，使得在相同撞击速度下桩基嵌固深度越深，所得墩顶位移越大。3倍模型、弹簧法和有限域法位移变化相差较小。

3)关于桥墩损伤特征，采用各桩土模型，其损伤机理与损伤部位相似，即桥墩受撞部位主要发生冲剪破坏，桥梁各构件的连接处往往是易损部位，因此在桥墩防撞设计中，应考虑桥墩整体结构，对各构件连接位置应予以重视。3种速度下，等效嵌固法模型桩基侧面不存在约束，造成其撞击特征点的应力值大于弹簧法和有限域法的情况，当进行桥墩应力分析时，后2种方法能较好地反映真实情况，更为合理。

综上所述，在桥墩受车撞分析中，应考虑桩土作用的影响，将桥墩立柱底端简化为固定边界所得响应往往偏小，在实际工程计算时可能造成较大偏差。在使用等效嵌固法进行计算时，推荐使用8倍嵌固模型。有限域土体法精度较高，但计算耗时是需要考虑的因素。等效弹簧法建模思路简单，是模拟桩土作用较好的方法。