支持向量机在PM2.5 预测研究中的应用

□文/石友山

（西安财经大学 陕西·西安）

［提要］ 支持向量机（SVM）是一种监督学习的方法，以统计学习理论为基础，主要用于进行分类和回归分析，是处理非线性回归的一种有效方法。近年来，西安雾霾事件频发，由于雾霾预测含有大量的非线性因素。对此，本文综合考虑湿度、温度、风级、实际二氧化硫浓度、二氧化氮浓度、一氧化碳浓度、臭氧浓度和PM10 浓度等因素，将粒子群算法（PSO）与支持向量机结合，通过构造PSO-SVM模型，对西安PM2.5 浓度进行预测。

引言

近年来，我国多地发生雾霾天气，西安是受雾霾影响较为严重的地区之一。当前，西安正处在城市化高速发展的重要阶段，为在2035 年之前基本实现现代化，使西安在“创新、协调、绿色、开放”等方面位于前列，成为国家中心城市，西安发展不能有丝毫懈怠。随着西安市经济的较快发展，城市开发力度不断增大，消耗能源的速度正在迅速增长，部分高能耗、重污染的企业占据西安市周边。而且由于西安地处黄土高原和秦岭山脉之间，冬季时西安市内排放暖气、工地扬尘增多，所造成的悬浮颗粒物没有扩散到西安市以外，使得雾霾构成物堆积在西安，极易出现大规模的雾霾现象。因此，政府和公众越来越关注雾霾的治理和预防，雾霾预测也显得尤为重要。

细颗粒物（PM2.5）是指大气中直径小于或等于2.5 微米的颗粒物，可被直接吸入人体，引发各种疾病，其数值越高，代表颗粒物浓度越高，意味着空气污染越严重。影响PM2.5 浓度的因素有空气中二氧化硫、二氧化氮、一氧化碳、可吸入颗粒物（PM10）、臭氧的含量和气象因素等。近年来，西安多次出现雾霾天气，对人们的生活产生了严重影响。PM2.5 是雾霾污染天气加重的主要因素，是描述雾霾天气的重要指标，故而对PM2.5 浓度的准确预测变得十分重要。分析PM2.5 浓度值变化规律对空气质量监测有重要意义。

对于非线性关系的雾霾预测问题来说，传统的统计预测方法很难解决。Vapnik 等人于1995 年在统计学习理论（SLT）基础上提出支持向量机（简称SVM），它是一种处理非线性回归的有效方法。SVM 为非线性的雾霾天气预测提供了一种可行的途径。本文利用与PM2.5 相关的多个变量建立支持向量机模型，然后通过粒子群算法对支持向量机的核心参数进行优化，建立了PSO-SVM 雾霾预测模型。

一、雾霾预测模型训练

（一）雾霾预测模型数据采集。气象因子和大气污染物对PM2.5 有着重要影响。气象因素与大气污染物的数据均来自真气网，本文选择2019 年1 月1 日～2021 年8 月31 日的PM2.5浓度数据和真气网的气象数据，主要包括AQI、PM2.5、PM10、SO2、NO2、CO、O3、温度、湿度、风级。

雾霾预测模型的数据集包括训练集和测试集，将原始数据进行划分，其中把随机选取的75%的数据（730 d）划分为训练集，剩下的25%的数据（244 d）划分为测试集。使用SVM 模型对训练集进行训练，使用测试集进行验证，将得到的结果与测试集真实的PM2.5 浓度进行对比，并计算平均绝对误差和均方根误差，验证预测的准确度。

（二）支持向量机模型。支持向量机算法中，通过算法将输入空间升维，与传统的方法思路不同。升维后，改变了内积的运算，问题在高维空间可以线性可分。并且在高维空间算法复杂性不受维数影响。SVM 模型具有如下优势：（1）针对小样本、有限样本可以获得理想的效果；（2）可以较好地处理非线性回归的问题；（3）计算量与样本维数基本无关，保证较好的泛化能力；（4）解决了模型选择、过拟合等问题，采用不同的核函数可以生成不同的SVM 算法。

建立基于支持向量机的雾霾浓度变化的预测模型，最重要的问题是选定合适的训练、测试样本，以及选择正确的预测模型结构主要参数。预测模型步骤为：

1、构建有效的自变量。由于雾霾浓度主要受大气污染和气象因子的影响，因此将前一天的AQI、PM10、SO2、NO2、CO、O3、温度、湿度与风级作为自变量。对输入的9 个变量进行数据降维，进而消除各变量间的相关性，剔除相关性较高的变量，留下相关性不高的因子，然后用留下来的7 个变量所构成的矩阵模型作为SVM 预测模型的输入因子。变量之间的相关关系如表1 所示。（表1）

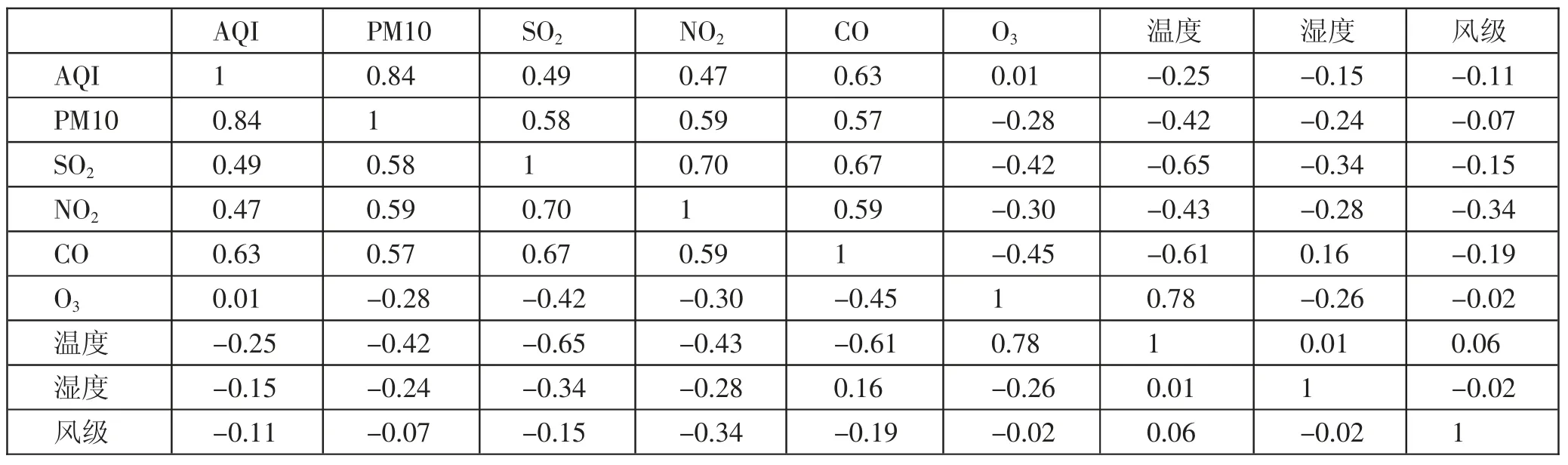
表1 变量之间相关关系一览表

2、选择核函数及参数值。建立试验，设定不同的核函数并建立SVM 预测模型，预测模型预测结果的MAE 和RMSE 如表2 所示。（表2）

根据表2 得知，高斯（RBF）核函数的平均相对误差和均方根误差较小，所以将RBF 设置为预测模型的核函数。惩罚因子C 的取值权衡了经验风险和结构风险。通过试验，设定不同惩罚因子C 并建立SVM 预测模型，设定其他参数不变，改变惩罚因子C 的数值（0～1，000），分析对RBF 核函数的影响，如表3所示。（表3）

表2 核函数平均相对误差和均方根误差一览表

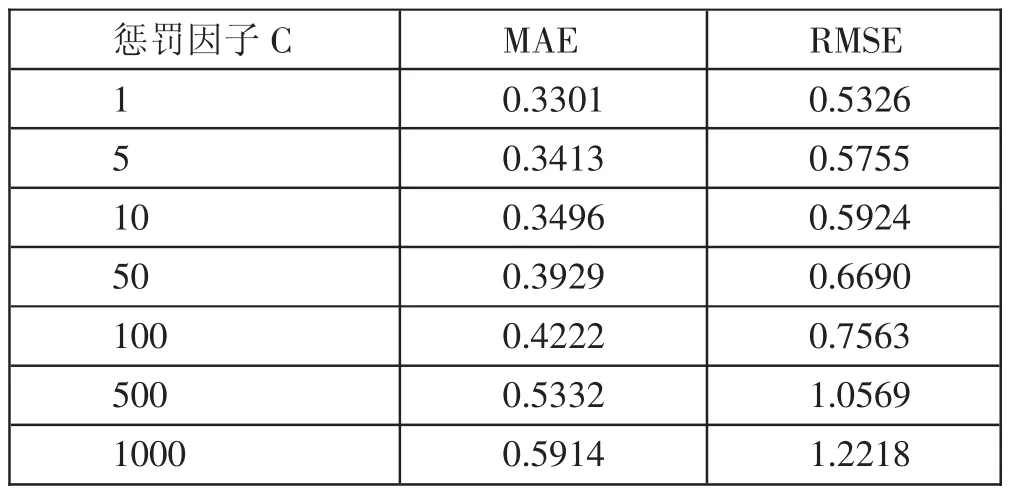
表3 惩罚因子C平均相对误差和均方根误差一览表

3、使用python 中的libsvm包对测试样本预测。使用传统的SVM（选用RBF 核函数），根据表3 选取最优的惩罚因子C=1，将预测样本放入模型中。预测结果如图1、图2 所示。（图1、图2）

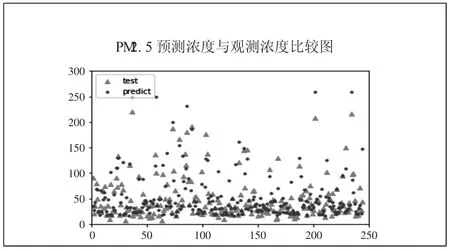
图1 PM2.5 预测浓度与观测浓度比较图

图2 测试样本预测图

PM2.5 浓度拟合效果一般，雾霾浓度与实际检测值有出入，预测结果不是很理想，总体误差有些大，决定系数只有0.6555，说明SVM 预测模型仍有较大的提升空间。需要对SVM的参数进行更为准确的设定，来提升预测的精确度。

（三）PSO-SVM预测模型。支持向量机算法中重要参数主要有核函数参数和惩罚系数，它的本质是一个优化搜索过程，本文提出粒子群优化算法（PSO）作为寻优技巧的SVM 建模参数调整方法。

粒子群算法最早是由两名美国的科学家基于鸟群觅食寻找最佳觅食区域的过程所提出来的一种基于种群的搜索算法。PSO 模拟的就是最佳决策的过程，鸟群觅食类似于人类的决策过程，从随机解出发，通过迭代寻找最优解，通过适应度来评价解的品质。建立SVM 模型需要设定惩罚因子C 和核函数σ。这两个参数值的选择都会对最终预测结果产生影响。因此，选取合适的参数对模型的预测效果十分重要，能够影响支持向量机的准确度及运算速率。

利用粒子群优化算法对待优化模型参数进行快速、全面的搜索，减少了试算产生的模糊定位，提高了模型预测的准确性。本文基于PSO-SVM 模型对参数进行了优化。首先，随机初始化总体，得到n 个粒子的总体，每个粒子代表参数的方向。将其作为SVM 参数进行迭代训练，记录下一次迭代得到的参数值。当迭代完成时，得到的粒子为适应度函数最大的粒子，该粒子表示使SVM 训练最优的SVM 参数。将该优化参数作为支持向量机预测参数进行预测，得到了预测结果。

初始化粒子群算法：首先，设置学习因子C1=2、C2=2，设置迭代次数的最大值为100，设置种群数量为20；完成初始化后，粒子将获得最优的惩罚参数C、核函数参数γ。其次，将最优的参数输入预测模型中，得到训练集的预测结果，其中粒子群的参数寻优适应度曲线如图3 所示。（图3）

图3 粒子群优化算法参数寻优的适应度曲线图

两个参数的寻优的结果分别是γ=0.001 以及C=3.70786491。将寻优参数带入到SVM 预测模型中，将预测样本输入到寻优后的预测模型。图4、图5 为基于PSO-SVM 模型的样本测试集预测结果。（图4、图5）

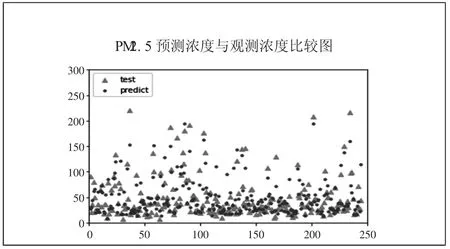
图4 PM2.5 预测浓度与观测浓度比较图

图5 测试样本预测图

PM2.5 通过使用PSO-SVM 建立的预测模型预测后拟合度更好，更具备线性特征。混合模型在经过参数寻优以后，对预测精度有明显提升，预测效果比SVM 模型预测效果好，决定系数达到0.7183。但依旧与实际值有出入，还需提升训练样本容量，确定更为精确的SVM 参数来提高模型的准确度。

二、模型预测结果评价

（一）评价标准。本文使用平均绝对误差（MAE）、均方根误差（RMSE）和决定系数（R2）对预测结果进行评价。

复相关系数R2的计算公式为：

其中，yi和分别表示真实值和预测值。

（二）各模型预测结果。以平均绝对误差（MAE）、均方根误差（RMSE）和决定系数（R2）作为评价指标，对不同模型的性能进行了评价，如表4 所示。（表4）

表4 各模型预测评价一览表

在表4 中，平均绝对误差（MAE）的排名从高到低为SVM（14.1827）、PSO-SVM（14.0210），均方根误差（RMSE）从高到低排名为SVM（23.4377）、PSO-SVM（21.1958），皮尔逊系数（R2）从高到低为PSO-SVM（0.7183）、SVM（0.6555）。实验表明，本文经过粒子群算法优化的支持向量机有了较高的提升，基于粒子群算法的支持向量机模型提高了对雾霾的预测准确度。

三、结论及建议

为提高对西安市雾霾的预测，考虑到雾霾影响因素复杂、非线性化的样本数据以及各类影响，本文提出粒子群优化的支持向量机的预测模型，混合模型提高了单一模型的预测精度。运用数据预测并结合以往数据规律来预防大气污染的发生，其结果对雾霾预测与防治有重要的实际意义。本文的主要研究结果：（1）对雾霾预测的研究现状进行简要介绍，探究支持向量机核函数、惩罚因子的选择，对于参数选择的问题，本文引入粒子群算法，并对粒子群算法做简单的介绍。分析支持向量机在非线性模型上的优势，对其预测流程进行了简单分析。（2）本文探究影响雾霾浓度的关键因素，进而将气象因素与空气污染物等影响因素作为雾霾的重要成因，分析了雾霾浓度与各种影响因子之间的联系，确定了7 种因素作为模型的输入样本。（3）本文选用SVM 模型和PSO-SVM 模型对雾霾做出预测。通过对比平均绝对误差、均方根误差和决定系数，认为PSO-SVM 混合预测模型的全局搜索能力较为优异，同时提升收敛速度与预测的相对精度，并且三种评价指标均为最优。

本文的样本数据只考虑了大气因素对雾霾浓度的影响，为提高模型的精确度，可以加入多维度的影响因子，如人口密度、绿化水平、城镇化水平等。细化需要预测的地域，可以提高其精确性，也可以学习一些其他优化算法，在本文算法的基础上尝试融合，并检验新混合模型的精确度。